Стистические методы. Решение Вероятность неукомплектованности автомобиля p0,2
 Скачать 51.1 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Тульский государственный университет» Контрольно-расчетное задание по дисциплине: «Статистические методы в транспортном машиностроении» Подготовил: студент гр.Б660752 Баранов М.О. Проверил: проф. доц. Селиверстов Г.В. Тула 2018г. Слово составленное из карточек, на каждой из которых написана буква. Карточки смешивают и вынимают без возварата по одной. Найти вероятность того, что карточки с буквами вынимаются в порядке следования букв заданного слова: а) событие, б) статистика. а) «событие» 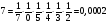 б) «статистика» 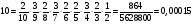 Вероятность выигрыша по облигации займа за все время его действия равна 0.25. Какова вероятность того, что некто, приобретя 8 облигаций, выиграет больше половины из них? Вероятность того, что из 8 облигаций выиграет ровно k облигаций, выражается формулой Бернулли: 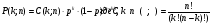 - число сочетаний из n по k,где в данном случае р=0,25, n=8, k может принимать значения от 0 до 8, т.е. 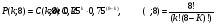 Вероятность того, что из n облигаций выиграют больше половины, сумме P(k;8) по k от 5 до 8: Р = P(5;8)+P(6;8)+P(7;8)+P(8;8) = 0,0231+0,0038+0,0004+0,0000 = 0,0273 = 2,73%. В среднем часть поступащих в продажу автомобилей некомплектны. Найти вероятность того, что среди десяти автомобилей имеют некомплектность: а) три автомобиля; б) менее трех. Решение: Вероятность неукомплектованности автомобиля: p=0,2 Вероятность того, что среди десяти автомобилей имеют некомплектность три автомобиля. 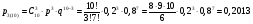 Менее трех ( укомплектованы два или один или ноль автомобилей). 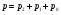 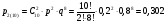 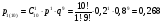 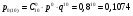 Получим: 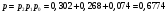 Стрелок ведет стрельбу по цели с вероятностью попадания при каждом выстреле 0,2. За каждое попадание он получает 5 очков, а в случае промаха очков ему не начисляют. Составить закон распределения числа очков, полученных стрелком за 3 выстрела, и вычислить математическое ожидание этой случайной величины. Решение. Случайная величина  может принимать 2 значения:0 – если стрелок промахнулся 3 раза; 5 – если стрелок попал 1 раз при трех выстрелах; 10 – если стрелок попал 2 раза при трех выстрелах; 15 – если стрелок попал 3 раза. Так как каждый выстрел можно рассматривать, как независимое испытание, в результате которого возможны только два исхода: попадание («успех») или промах («неудача»), то вероятности, соответствующие каждому значению случайной величины, можно найти по формуле Бернулли (5):  .По условию задачи имеем: число испытаний  , вероятность успеха P=0,2 , q=1-p=1-0,2=0,8 значения 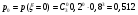 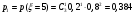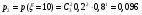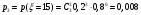будут изменяться от 0 до 3. Т.о. имеем:    Следовательно, окончательно закон распределения случайной величины будет иметь вид:
Слово составлено из карточек, на каждой из которых написана одна буква. Затем карточки перемешивают и вынимают без возврата по одной. Найти вероятность того, что буквы вынимаются в порядке слова «СТАТИСТИКА». Решение. Испытание заключается в вынимании карточек с буквами в следующем порядке без возврата. Элементарным событием является полученная последовательность букв. Событие А состоит в получении нужного слова СТАТИСТИКА. Элементарные события являются перестановками из 10 букв, значит n=10!. Некоторые буквы в слове повторяются, поэтому возможны перестановки, при которых слово не изменяется. Найдем это число. Буква «С» встречается в слове – 2 раза, «А» - 2, «Т» - 3, «И» - 2, «К» - 1. Т.о.  Тогда,  .Ответ:  . |
