Матан_решение_20 вар.. Решение Вычислим данные частные производные Ответ Кр Задание 100
 Скачать 439.5 Kb.
|
|
Кр № 2. Задание 60. Найти  для функции  . Решение: Вычислим данные частные производные: 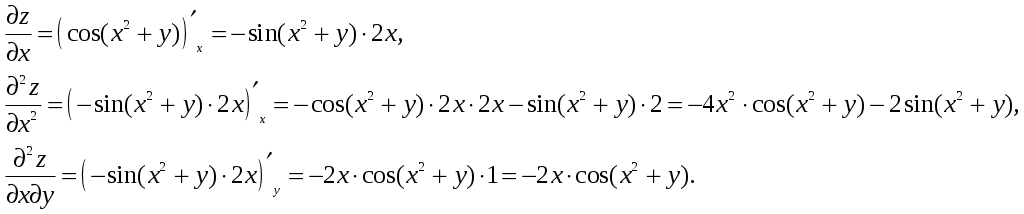 Ответ:  Кр № 2. Задание 100. Проинтегрировать дифференциальное уравнение. При заданном начальном условии найти соответствующий частный интеграл или частное решение.  Решение: Данное уравнение является уравнением с разделяющимися переменными, решим его: 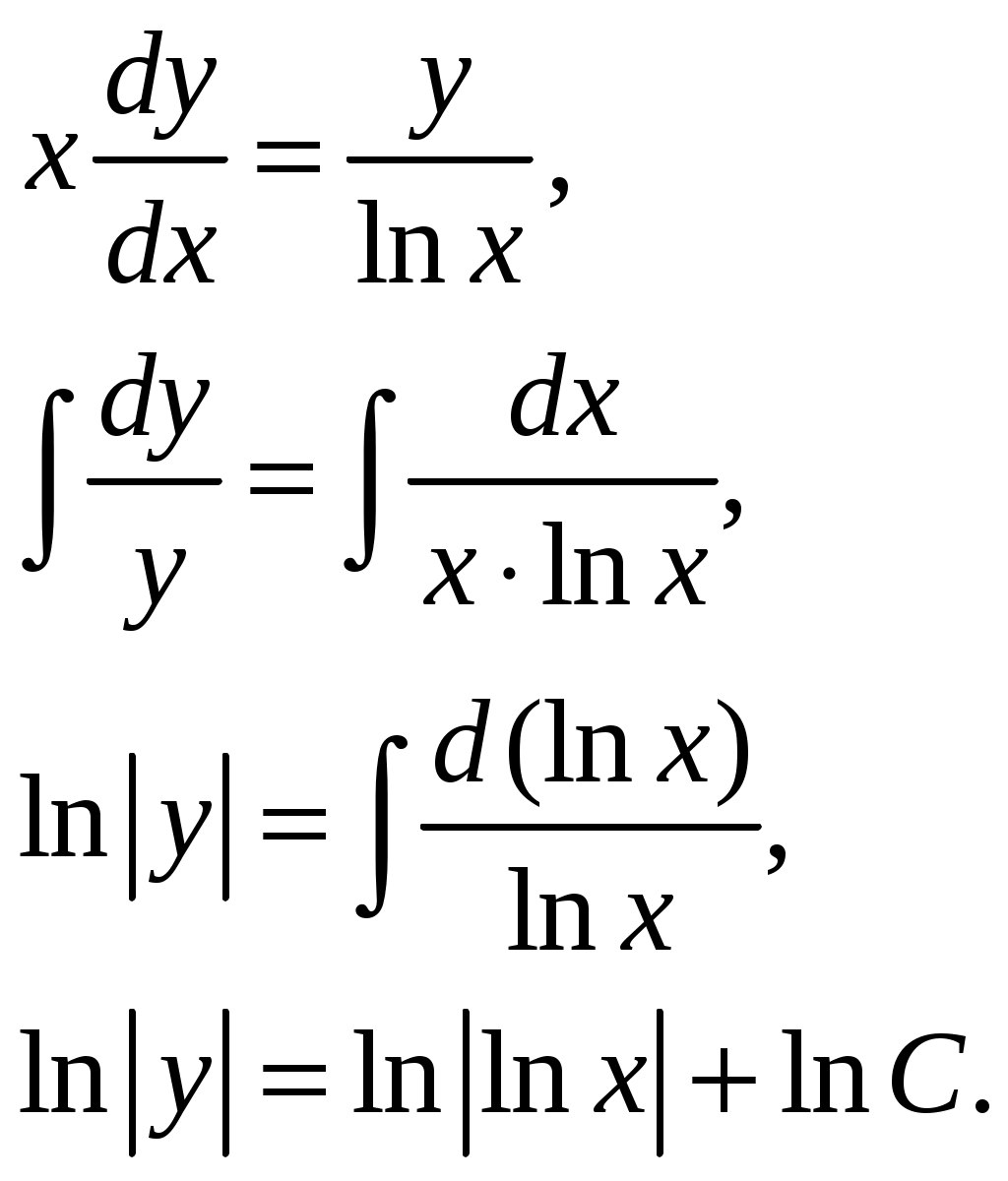  – общее решение дифференциального уравнения.Найдем частное решение, удовлетворяющее условию:    – частное решение исходного дифференциального уравнения.Ответ: .Кр № 2. Задание 140. Найти общее решение уравнения.  Решение: Данное уравнение является неоднородным дифференциальное уравнением 2го порядка. Решение будем искать в виде:  где  – общее решение однородного дифференциального уравнения,  – частное решение неоднородного дифференциального уравнения.Найдем общее решение соответствующего однородного уравнения:  .Составим и решим характеристическое уравнение:  ,   Общее решение имеет вид:  , где  . Рассмотрим правую часть исходного уравнения:  Частное решение ищем в виде:  . Находим производные:  Подставим выражение  ,  в исходное уравнение: Приравняв коэффициенты при одинаковых степенях, получим систему: 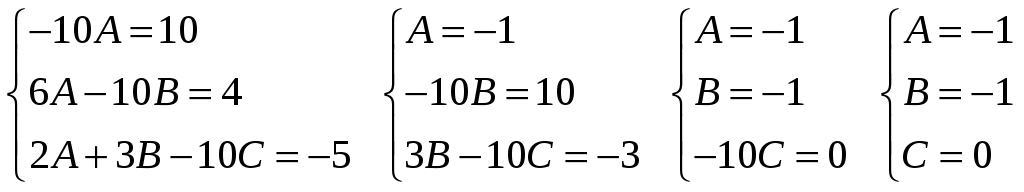 .Тогда  Общее решение исходного уравнения имеет вид где .Ответ: где .Кр № 3. Задание 1. Исследовать на сходимость числовые ряды, пользуясь известными признаками сходимости. 1.20. а)  ; б)  Решение: а) Воспользуемся интегральным признаком Коши. 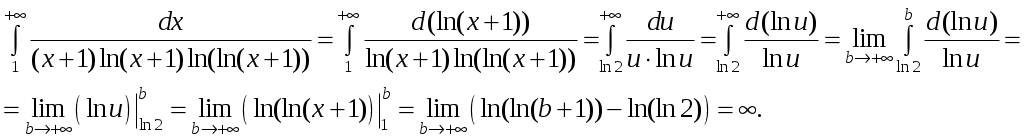 Подынтегральная функция непрерывна на  . Значит, исходный ряд расходится вместе с соответствующим расходящимся несобственным интегралом. б)Воспользуемся признаком Даламбера: 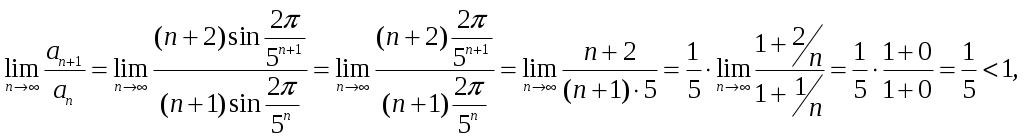  значит, исследуемый ряд сходится. Ответ: а) ряд расходится; б) ряд сходится. Кр № 3. Задание 4. Вычислить с помощью двойного интеграла площадь плоской области D, ограниченной заданными линиями. 4.20.  Решение:  Находим точки пересечения линий. Для этого приравняем правые части уравнений:  т.е. точки пересечения  Строим заданные линии на плоскости XOY: 1) точки пересечения параболы  с осью OX: 2) через точки A и Bпроводим прямую. Через точку  на оси OX и точки A и B проводим параболу. Получаем область, ограниченную линиями, площадь которой необходимо вычислить;Из свойств интеграла по фигуре следует, что площадь S плоской области D в декартовых прямоугольных координатах равна: 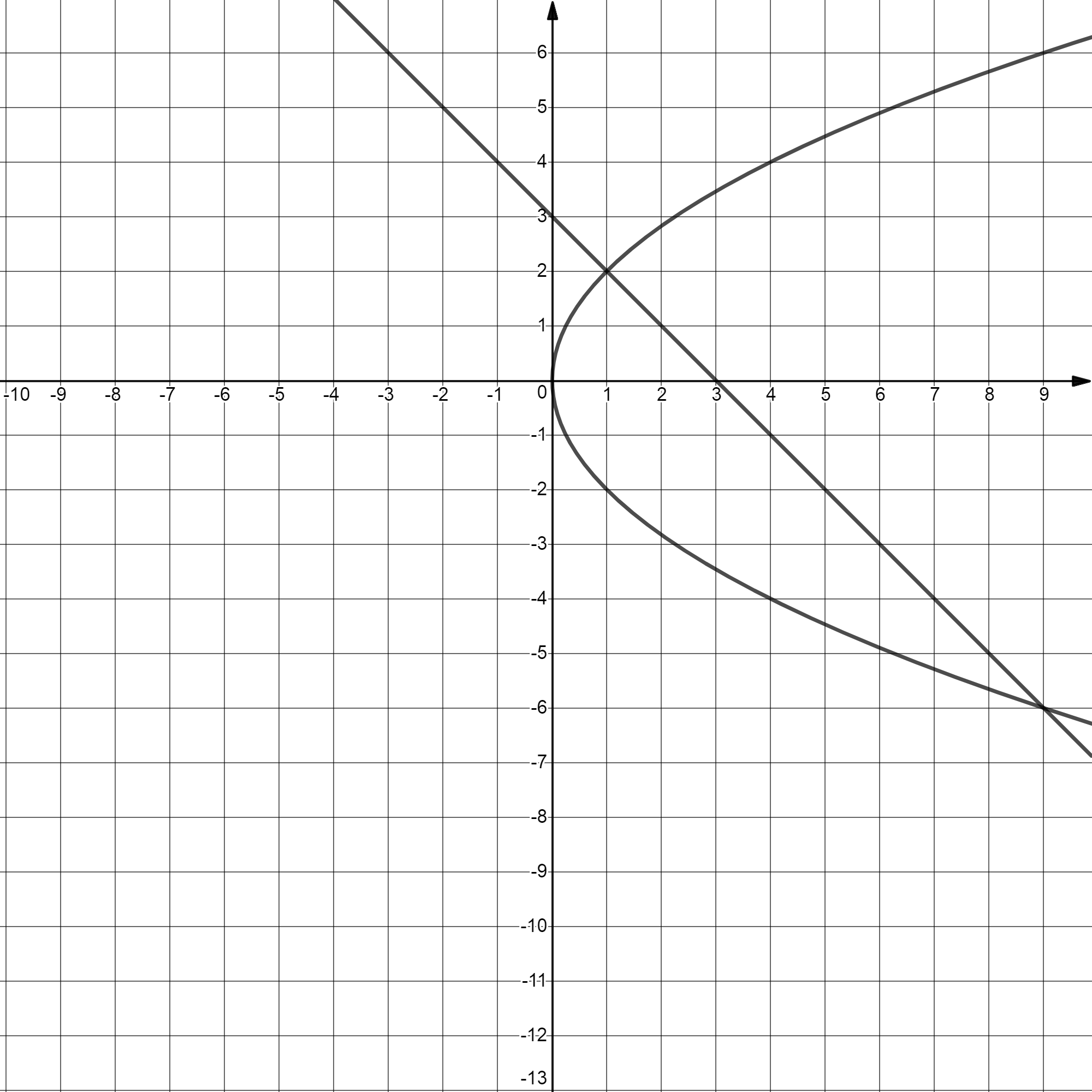   y x       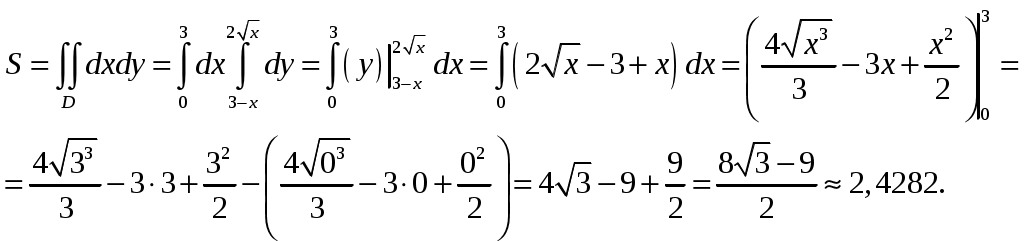 Ответ:  |