гадасин задачи. Решение Вычислим какое количество времени занимает передача файла по каналу связи без архивации

• Название: Решение Вычислим какое количество времени занимает передача файла по каналу связи без архивации
• Дата: 10.10.2022
• Размер: 1.16 Mb.
• Имя файла: гадасин задачи.docx
• Тип: Задача; #725630
• страница: 4 из 12

Задача 8

Закодировать символ методом Шеннона-Фано, который соответствует требованию оптимального кодирования. Провести анализ текста, определить вероятность наличия символа в тексте, включая пробелы и построить таблицу кодов символов методом Шеннона-Фано.
Способ решения

Алгоритм построения кода Шеннона-Фано состоит в том, что кодируемые символы (буквы) разделяются на две равновероятные подгруппы: для символов 1-й подгруппы на втором месте ставится 0, а для 2-й подгруппы – 1 и т.д.

Для каждой буквы определяется вероятность ее появления в тексте. Вероятности сортируются по убыванию. Берутся первые n букв до тех пор, пока n+1 не станет больше 0,5. Первые n букв будут иметь на первом месте 0, остальные 1. Далее каждой из групп производится нормировка вероятностей исходя из их суммы и для каждой из двух групп повторяется предыдущий шаг.

Процесс продолжается до тех пор, пока в каждом подразделении не окажется ровно одна буква, которая и будет закодирована определенным двоичным кодом.
Пример

Пусть, исходя из анализа текста была выявлена вероятность появления каждой буквы, равная отношению количества появления отдельной буквы, к общему количеству символов (Таблица 9):
Таблица 9. Вероятность появления буквы

А	В	Л	И	Е	С	К
0,3	0,2	0,15	0,1	0,1	0,08	0,07

Исходя из исходных данных Таблицы 9 и Способа решения все исходные символы были закодированы методом Шеннона-Фано (Таблица 10).
Таблица 10. Кодировка исходных символов методом Шеннона-Фано

буу буква	вероятности	символы кода					код
А	0,30	0	0			00
В	0,20		1			01
Л	0,15	1	0	0		100
И	0,10			1		101
Е	0,10		1	0		110
С	0,08			1	0	1110
К	0,07				1	1111

Исходный текст, который используется для решения Задачи 8

Энтропия в теории информации есть мера или степень неопределенности ситемы В теории информации под энтропией понимается мера неопределенности источника сообщений определяемая вероятностями появления тех или иных символов при их передаче В математике и кибернетике информация является мерой устранения неопределенности энтропии мерой организации системы Соотношение между понятиями энтропия и информация в известном смысле напоминает соотношение между физическими понятиями потенциала и разности потенциалов Энтропия это количественная мера неопределенности Уничтоженная сведениями энтропия и есть информация В этом смысле информация выступает как мера отношения взаимосвязи между системами явлениями процессами а не как показатель состояния систем Пространство событий играет важную роль в геометрической интерпретации теории относительности Каждое событие характеризуется положением координатами и временем поэтому множество всевозможных событий оказывается четырёхмерным Пространством где точка событие определяется четырьмя координатами Пространство связано со временем через событие а исходя из того что пространство и время всеобщие формы существования материи и пространство и время не существуют вне материи и независимо от неё то событие существует всегда там где есть пространство и время Событие познается человеком через информацию Совокупность информации формирует событие то есть является точкой в событии Исходя из этого информация также имеет как пространственную так и временную координаты и так же является мерой соотношения между пространством и временем

Таблица 11. Исходные данные для решения Задачи 8

№ варианта	строка
	начальная	конечная
1	1	8
2	2	9
3	3	10
4	4	11
5	5	12
6	6	13
7	7	14
8	8	15
9	9	16
10	10	17
11	11	18
12	12	19
13	13	20
14	14	21
15	15	22
16	16	23
17	17	24
18	18	25
19	19	26
20	20	27
21	21	28
22	22	29
23	23	30
24	24	31
25	25	32

Задача 9

Код Шеннона-Фано - неравномерный код. Чтобы он был оптимальным, необходимо, чтобы средняя длина кодовой комбинации для определенного алфавита, закодированного этим кодом, была меньше длины кодовой комбинации равномерного двоичного кода, которым можно закодировать этот алфавит.

Оценить оптимальность кода для сообщения, построенного по методу Шеннона-Фано исходя из:

1. 
   Алфавита сообщения, см. Задачу 8 для своего варианта;
   
2. 
   Алфавита русского языка.
   

Решение

Решим задачу для примера сообщения: ВИСЕЛАСЛИВА

1. 
   Рассчитаем энтропию источника сообщений
   

Воспользуемся данными из Таблицы 9: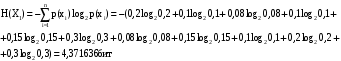



Воспользуемся данными из Таблицы 10: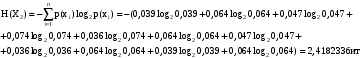

2. 
   Определим среднее число элементарных символов на символ сообщения как произведение количества символов кода, которым закодирован символ, на вероятность появления данного символа.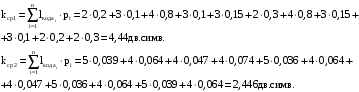
   

3. 
   Рассчитаем количество информации на один элементарный символ: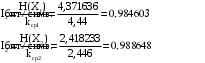
   

Таким образом, информация, приходящаяся на один символ, рассчитанная исходя из вероятности появления символа в наборе символов меньше чем исходя из вероятности появления символа русского алфавита. Исходя из того, что оба значения близки к своему верхнему пределу 1, и оба кода отвечают принципу оптимальности, код, базирующийся на частоте букв русского алфавита, является более оптимальным.
Таблица 12. Вероятность появления букв в русском алфавите

буква	частота	буква	частота	буква	частота
- о е а и т н с р в л	0,145 0,095 0,074 0,064 0,064 0,056 0,056 0,047 0,041 0,039 0,036	к м д п у я ы з ъ, ь б г	0,029 0,026 0,026 0,024 0,021 0,019 0,016 0,015 0,015 0,015 0,014	ч й х ж ю ш щ э ф	0,013 0,01 0,009 0,008 0,007 0,006 0,003 0,003 0,002

Таблица 13. Код Шеннона-Фано для букв русского алфавита исходя из данных Таблицы 12

буквы	вероят ности	символы кода
		1-й	2-й	3-й	4-й	5-й	6-й	7-й	8-й	9-й	код
- о е а и т н с р в л к м д п у я ы з ъ, ь б г ч й х ж ю ш ц щ э ф	0,145 0,095 0,074 0,064 0,064 0,056 0,056 0,047 0,041 0,039 0,036 0,028 0,026 0,026 0,024 0,021 0,019 0,016 0,015 0,015 0,015 0,014 0,013 0,01 0,009 0,008 0,007 0,006 0,003 0,003 0,003 0,002	0	0	0							000 001 0100 0101 0110 0111 1000 1001 10100 10101 10110 10111 11000 11001 11010 110110 110111 111000 111001 111010 111011 111100 111101 1111100 11111010 11111011 11111100 11111101 111111100 111111101 111111110 111111111
				1
			1	0	0
					1
				1	0
					1
		1	0	0	0
					1
				1	0	0
						1
					1	0
						1
			1	0	0	0 1
					1	0
						1	0
							1
				1	0	0	0
							1
						1	0
							1
					1	0	0
							1
						1	0	0
								1	0 1
							1	0	0
									1
								1	0	0
										1
									1	0
										1