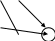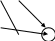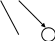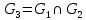Дискретная математика. Дискретная математика решение. Решение Возьмём неравенство Рассмотрим уравнение
 Скачать 175.49 Kb. Скачать 175.49 Kb.
|
|
Практическое задание 1 Тема 1. Множества, соответствия, отношения Пусть A, B, C, - множество точек плоскости, координаты которых удовлетворяют условиям 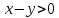 , ,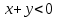 и и 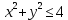 соответственно. Изобразите в системе координат x0y множество D, полученное из множеств A, B и C по формуле соответственно. Изобразите в системе координат x0y множество D, полученное из множеств A, B и C по формуле 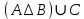 . .Решение: Возьмём неравенство: 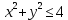 . .Рассмотрим уравнение: 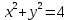 . .Мы получили уравнение окружности с центром в точке (0,0) и радиусом 2. 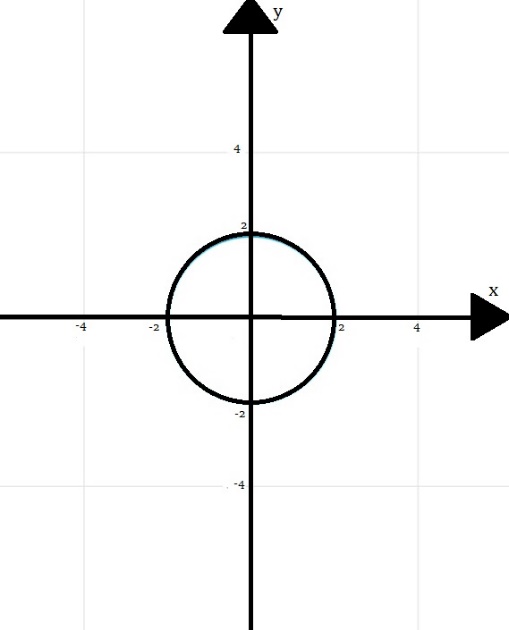 Возьмем пробную точку (0,1) и подставим её в неравенство: 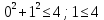 . .Эта точка удовлетворяет неравенству. Следовательно, неравенству соответствует внутренняя часть окружности. 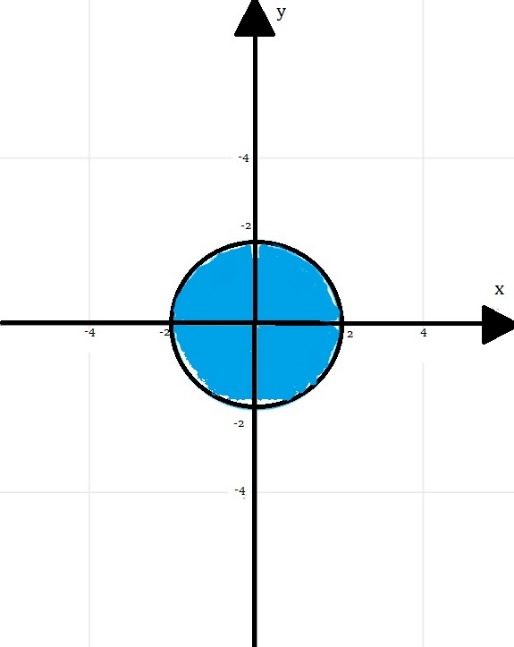 Выяснить взаимное расположение множеств D, E, F, если А, В, Х – произвольные подмножества универсального множества U.
Решение: Используем диаграмму Эйлера-Венна. 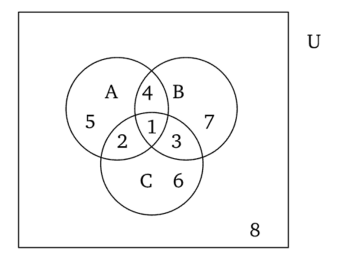 U= {1,2,3,4,5,6,7,8}, A= {1,2,4,5}, B= {4,5,6,7}, X= {2,3,5,7}. 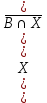 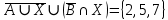 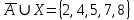 Практическое задание 2 Тема 2. Основные формулы комбинаторики 1. Сколькими способами из колоды в 36 листов можно выбрать не упорядоченный набор из 5 карт так, чтобы в этом наборе было бы точно: 3 туза, 3 карты черной масти Решение: 3 туза 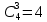 - количество способов, достать 3 туза из 4-х - количество способов, достать 3 туза из 4-х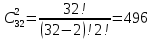 – количество способов (в дополнение к этим трём тузам) достать оставшиеся 2 карты из 32-х – количество способов (в дополнение к этим трём тузам) достать оставшиеся 2 карты из 32-х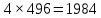 – общее количество способов – общее количество способов 3 карты черной масти: 2 пары карт черной масти 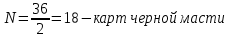 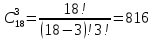 Общее количество способов: 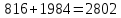 Ответ: 2802 2. Сколько различных слов можно получить перестановкой букв слова a?
Решение: 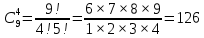 Ответ: 126 способов. 3. Найти наибольший член разложения бинома 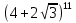 Пусть 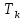 - наибольший член разложения бинома - наибольший член разложения бинома 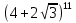 , ,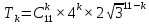 . .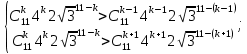 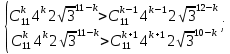 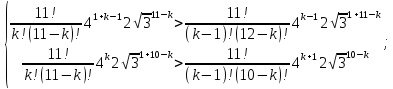 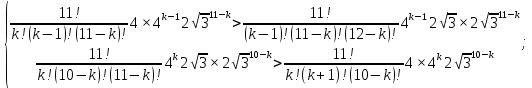 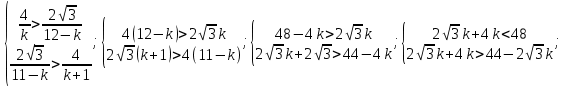 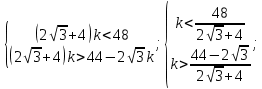 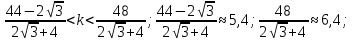 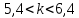 т.к. 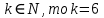 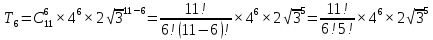 Ответ: Наибольший член разложения бинома 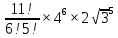 . .Найти коэффициенты при x22 в разложении данного выражения (3-x2+x5)12 по полиномиальной формуле, полученный после раскрытия скобок и приведения подобных членов. Решение: 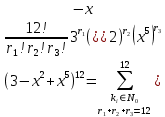 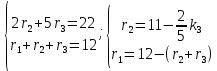 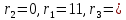 0 0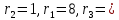 2 2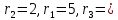 4 4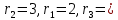 6 6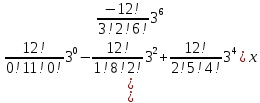 Практическое задание 3 Тема 4. Нормальные формы. Тупиковая, минимальная и сокращенная ДНФ Для данных функций 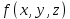 и и 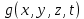 , заданных векторно в , заданных векторно в
, проделать следующее: 1. Записать их СДНФ и СКНФ. 2. Методом Квайна найти сокращённую ДНФ. 3. Для сокращенной ДНФ построить матрицу Квайна, указать ядровые импликанты. 4. С помощью матрицы Квайна найти минимальную ДНФ, указать её сложность. 5. Найти минимальную ДНФ данной функции с помощью карт Карнау, сравнить полученный результат с ДНФ, найденной в п.4. Решение: Таблицы истинности функций.
СДНФ: 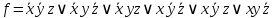 , ,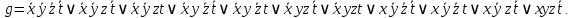 СКНФ: 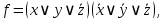 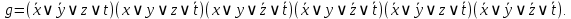 Сокращенная ДНФ: 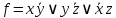 . .
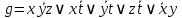 . .Получение из сокращенной ДНФ минимальной ДНФ с помощью матрицы Квайна.
4. Для функции 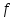 все три импликанты являются ядровыми. Поэтому сокращённая ДНФ является и минимальной, её сложность равна 6. все три импликанты являются ядровыми. Поэтому сокращённая ДНФ является и минимальной, её сложность равна 6.Для функции 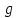 ядровыми импликантами являются 1, 2, 3, и 5. ядровыми импликантами являются 1, 2, 3, и 5. Минимальная ДНФ: 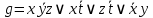 , её сложность равна 12. , её сложность равна 12.5. Найдем минимальную ДНФ с помощью карт Карнау.
Практическое задание 4 Тема 7. Полные и двудольные графы. Операции над графами. Связность. Диаметр, радиус, центр графа Даны графы G1 и G2. В таблице 3.1. 1. Найдите G1G2, G1∩G2, G1G2 аналитически и изобразить результат графически. 2. Для графа G=G1G2 найдите матрицу смежности, матрицу инцидентности, компоненты сильной связности, маршруты (но не цепи) длины 7; простые цепи, простые циклы, исходящие из вершины 1. С помощью матрицы смежности определите количество путей длины 2, 3, 4 из вершины 1 в вершину 4, из вершины 2 в вершину 4, выясните имеются ли контуры в графе. 3. Найдите степени всех вершин, радиус и диаметр графа G. 4. Является ли граф G эйлеровым, если нет, то постройте эйлеров цикл.
Решение:
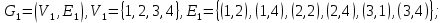 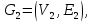 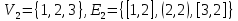 . .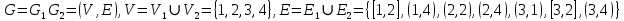
G=G1G2 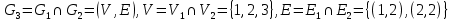
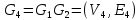 , , 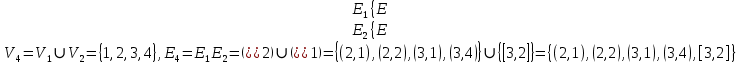 , ,
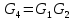 2. Матрица смежности 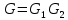 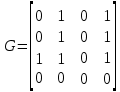 Матрица инцидентности.  , , 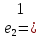 ,4), ,4), 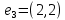 , , 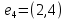 , , 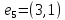 , , 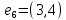 , , 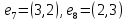 . .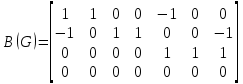 . .Матрица связанности. 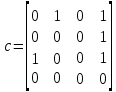 Граф 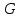 имеет один компонент связности {1, 2, 3}. имеет один компонент связности {1, 2, 3}.1 2  3 Маршрут: 1 – 2 – 3. Циклы: 1 – 2 – 4 – 1, 1 – 3 – 4 – 1. . Цепи: 1 – 2 – 4, 1 – 3 - 4. Из вершины 1 в вершину 4, следует 1 путь. Из вершины 2 в вершину 4, следует 1 путь. 3. Радиус = 1 (1 – 2). Диаметр = 2 (3 – 1 – 2). Вершина 1 = 2 степень, вершина 2 = 3 степень, вершина 3 = 2 степень, вершина 4 вершина = 0. 4. Эйлеров цикл: 1 – 2 – 4 - 3 – 1. 1 2  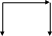 3 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

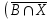 \ А) (Х\В)
\ А) (Х\В)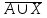 (
(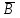 X)
X)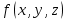
 простые импликанты
простые импликанты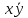
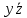
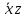
 простые импликанты
простые импликанты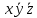
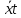
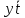
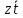
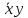
 yz
yz

 1
1
 1
1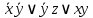 , сложность равна шести. Эта полученная минимальная ДНФ отличается от полученной в пункте 4. Сложности полученных ДНФ одинаковые.
, сложность равна шести. Эта полученная минимальная ДНФ отличается от полученной в пункте 4. Сложности полученных ДНФ одинаковые. 
 1
1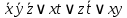 , совпадает с полученной в пункте 4.
, совпадает с полученной в пункте 4.