Решение задач Аннотация. Урок посвящен циклу for

• Название: Решение задач Аннотация. Урок посвящен циклу for
• Дата: 28.06.2022
• Размер: 3.04 Mb.
• Имя файла: 5. Python.docx
• Тип: Решение; #618203
• страница: 18 из 23

Производительность кода

Под производительностью кода в простейшем случае можно подразумевать то, сколько времени программа тратит на решение задачи. При написании программы, программист должен думать над тем, сколько времени в худшем случае потребуется его программе для решения задачи.

Рассмотрим задачу, которая проверяет число на простоту.

1 версия программы: Перебираем все числа от 2 до num - 1 и делаем проверку делимости числа num на i:

num = int(input())

flag = True

for i in range(2, num):

if num % i == 0:

flag = False

if num > 1 and flag == True:

print('Число простое')

else:

print('Число составное')

Если программе на вход подается простое число num = 1934234249, то она будет работать примерно 270270 секунд = 4.54.5 минуты.🙄

2 версия программы: Несложно понять, что перебирать все числа от 2 до num - 1 не имеет смысла. Достаточно проверить числа от 2 до num // 2 + 1:

num = int(input())

flag = True

for i in range(2, num // 2 + 1):

if num % i == 0:

flag = False

if num > 1 and flag == True:

print('Число простое')

else:

print('Число составное')

Если программе на вход подается простое число num = 1934234249, то она будет работать примерно 130130 секунд = 2.22.2 минуты. По сути мы улучшили время работы программы вдвое! 😊

3 версия программы: Правую границу num // 2 + 1 проверки можно улучшить, если заметить, что у любого составного числа есть делитель (отличный от 1), не превосходящий квадратного корня из числа. Таким образом, имеет смысл перебирать делители от 2 до 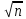 ​+1.

num = int(input())

flag = True

for i in range(2, int(num ** 0.5) + 1):

if num % i == 0:

flag = False

if num > 1 and flag == True:

print('Число простое')

else:

print('Число составное')

Если программе на вход подается простое число num = 1934234249, то она будет работать примерно 0.0660.066 секунд. По сути мы улучшили время работы программы в 4000 раз! 😎

4 версия программы: Предыдущие оптимизации касались случая, когда проверяемое число является простым. В случае если число является составным и мы нашли его первый делитель (отличный от 1), мы прерываем цикл с помощью оператора break:

num = int(input())

flag = True

for i in range(2, int(num ** 0.5) + 1):

if num % i == 0:

flag = False

break

if num > 1 and flag == True:

print('Число простое')

else:

print('Число составное')