Решение задач Аннотация. Урок посвящен циклу for

• Название: Решение задач Аннотация. Урок посвящен циклу for
• Дата: 28.06.2022
• Размер: 3.04 Mb.
• Имя файла: 5. Python.docx
• Тип: Решение; #618203
• страница: 23 из 23

Таблица-1

Дано натуральное число n (n≤ 9). Напишите программу, которая печатает таблицу размером n×3 состоящую из данного числа (числа отделены одним пробелом).

Формат входных данных
На вход программе подается одно натуральное число.

Формат выходных данных
Программа должна вывести таблицу размером n×3 состоящую из данного числа.

Примечание. В конце строки может быть пробел.

5. Таблица-2

Дано натуральное число n (n≤ 9). Напишите программу, которая печатает таблицу размером n×5, где в i-ой строке указано число i (числа отделены одним пробелом).

Формат входных данных
На вход программе подается одно натуральное число.

Формат выходных данных
Программа должна вывести таблицу размером n×5 в соответствии с условием.

Примечание. В конце строки может быть пробел.

6. Таблица-3

Дано натуральное число n (n≤ 9). Напишите программу, которая печатает таблицу сложения для всех чисел от 1 до n в соответствии с примером.

Формат входных данных
На вход программе подается одно натуральное число.

Формат выходных данных
Программа должна вывести таблицу сложения для всех чисел от 1 до n.

Примечание. В конце строки может быть пробел.

7. Звездный треугольник 🌶️🌶️

Дано нечетное натуральное число n. Напишите программу, которая печатает равнобедренный звездный треугольник с основанием, равным n в соответствии с примером:

*

**

***

****

***

**

*

Формат входных данных
На вход программе подается одно нечетное натуральное число.

Формат выходных данных
Программа должна вывести треугольник в соответствии с условием.

Примечание. Используйте вложенный цикл for.

8. Численный треугольник 1

Дано натуральное число n. Напишите программу, которая печатает численный треугольник в соответствии с примером:

1

22

333

4444

55555

...

Формат входных данных
На вход программе подается одно натуральное число.

Формат выходных данных
Программа должна вывести треугольник в соответствии с условием.

Примечание. Используйте вложенный цикл for.

Использование вложенных циклов при решении уравнений

Вложенные циклы можно использовать для решения уравнений с несколькими переменными. Зная, что решения (корни) уравнения являются натуральными (целыми) числами, несложно написать программу, содержащую вложенный цикл и перебирающую все возможные значения переменных.

Решение задач

Задача 1. Найдите все пары натуральных чисел (и их количество) являющихся решением уравнения 12x+13y=777.

Решение. Поскольку по условию числа x и y являются натуральными, то x≤64,y≤59 . Напишем программу, которая перебирает всевозможные пары чисел (x;y) и проверяет для них выполнение условия 12x+13y=777.

total = 0

for x in range(1, 65):

for y in range(1, 60):

if 12 * x + 13 * y == 777:

total += 1

print('x =', x, 'y =', y)

print('Общее количество натуральных решений =', total)

В результате выполнения такого кода, мы получим:

x = 3 y = 57

x = 16 y = 45

x = 29 y = 33

x = 42 y = 21

x = 55 y = 9

Общее количество натуральных решений = 5

Задача 2. Найдите все пары натуральных чисел (и их количество) являющихся решением уравнения  x²+y²+z²=2020.

Решение.  Поскольку по условию числа x, y и z являются натуральными, то x,y,z≤ ​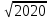=45. Напишем программу, которая перебирает всевозможные тройки чисел (x;y;z) и проверяет для них условие x²+y²+z²=2020.

total = 0

for x in range(1, 45):

for y in range(1, 45):

for z in range(1, 45):

if x ** 2 + y ** 2 + z ** 2 == 2020:

total += 1

print('x =', x, 'y =', y, 'z =', z)

print('Общее количество натуральных решений =', total)

В результате выполнения такого кода, мы получим:

x = 18 y = 20 z = 36

x = 18 y = 36 z = 20

x = 20 y = 18 z = 36

x = 20 y = 36 z = 18

x = 36 y = 18 z = 20

x = 36 y = 20 z = 18

Общее количество натуральных решений = 6

ЗАДАЧИ

1. 
   12 месяцев
   

Решите уравнение в натуральных числах 28n+30k+31m=365.

Примечание. Используйте вложенный цикл for. В первую очередь запишите решение с наименьшим значением n.

n = 
k = 
m = 
или
n = 
k = 
m = 

2. 
   Старинная задача
   

Имеется 100 рублей. Сколько быков, коров и телят можно купить на все эти деньги, если плата за быка – 10 рублей, за корову – 5 рублей, за теленка – 0.5 рубля и надо купить 100 голов скота?

Примечание. Используйте вложенный цикл for.

Количество быков: 
Количество коров: 
Количество телят: 

3. Гипотеза Эйлера о сумме степеней 🌶️🌶️

В 1769 году Леонард Эйлер сформулировал обобщенную версию Великой теоремы Ферма, предполагая, что по крайней мере n энных степеней необходимо для получения суммы, которая сама является энной степенью для n>2. Напишите программу для опровержения гипотезы Эйлера (продержавшейся до 1967 года), и найдите четыре положительных целых числа, сумма 5-х степеней которых равна 5-й степени другого положительного целого числа.

Таким образом, найдите пять натуральных чисел a,b,c,d,e удовлетворяющих условию:



В ответе укажите сумму a+b+c+d+e.

Примечание 1. Используйте вложенный цикл for.

Примечание 2. Считайте, что числа a,b,c,d,e не превосходят 150.

Примечание 3. Программа может работать дольше чем обычно. В зависимости от способа решения задачи на выполнение программы может уходить до нескольких минут. Попробуйте сократить количество вложенных циклов. 

4. Численный треугольник 3

Дано натуральное число n. Напишите программу, которая печатает численный треугольник с высотой равной n, в соответствии с примером:

1

2 3

4 5 6

7 8 9 10

11 12 13 14 15

16 17 18 19 20 21

...

Формат входных данных
На вход программе подается одно натуральное число.

Формат выходных данных
Программа должна вывести треугольник в соответствии с условием.

Примечание. Используйте вложенный цикл for.

5. Численный треугольник 4

Дано натуральное число n. Напишите программу, которая печатает численный треугольник с высотой равной n, в соответствии с примером:

1

121

12321

1234321

123454321

...

Формат входных данных
На вход программе подается одно натуральное число.

Формат выходных данных
Программа должна вывести треугольник в соответствии с условием.

Примечание. Используйте вложенный цикл for.

6. Делители-1 🌶️

На вход программе подается два натуральных числа a и b (a< b). Напишите программу, которая находит натуральное число из отрезка [a;b] с максимальной суммой делителей.

Формат входных данных
На вход программе подаются два числа, каждое на отдельной строке.

Формат выходных данных
Программа должна вывести два числа на одной строке, разделенных пробелом: число с максимальной суммой делителей и сумму его делителей.

Примечание. Если таких чисел несколько, то выведите наибольшее из них.

7. Делители-2

На вход программе подается натуральное число n. Напишите программу, выводящую графическое изображение делимости чисел от 1 до n включительно. В каждой строке надо напечатать очередное число и столько символов «+», сколько делителей у этого числа.

Формат входных данных
На вход программе подается одно натуральное число.

Формат выходных данных
Программа должна вывести графическое изображение чисел от 1 до n, каждое на отдельной строке.

8. Цифровой корень

На вход программе подается натуральное число n. Напишите программу, которая находит цифровой корень данного числа. Цифровой корень числа n получается следующим образом: если сложить все цифры этого числа, затем все цифры найденной суммы и повторить этот процесс, то в результате будет получено однозначное число (цифра), которое и называется цифровым корнем данного числа.

Формат входных данных
На вход программе подается одно натуральное число.

Формат выходных данных
Программа должна вывести цифровой корень введенного числа.

Примечание. Используйте вложенные циклы while.

9. Сумма факториалов

Дано натуральное число n. Напишите программу, которая выводит значение суммы 1!+2!+3!+…+n!.

Формат входных данных
На вход программе подается одно натуральное число.

Формат выходных данных
Программа должна вывести значение суммы 1!+2!+3!+…+n!.

Примечание 1. Факториалом натурального числа n, называется произведение всех натуральных чисел от 1 до n, то есть n!=1⋅2⋅3⋅…⋅n

Примечание 2. Задачу можно решить без вложенного цикла. Напишите две версии программы =)

10. Простые числа

На вход программе подается два натуральных числа a и b (a< b). Напишите программу, которая находит все простые числа от a до b включительно.

Формат входных данных
На вход программе подаются два числа, каждое на отдельной строке.

Формат выходных данных
Программа должна вывести все простые числа от a до b включительно, каждое на отдельной строке.

Примечание. Число 1 простым не является.