РГР Логистика. РГР_М_1_. Решение задач линейного программирования в пакетах Mathcad и ms excel
 Скачать 1.5 Mb.
|
Лабораторная работа 2. Решение транспортной задачи в пакете MS Excel.Транспортная задача – это задача о минимизации транспортных расходов, связанных с обеспечением пунктов потребления определенным количеством однородной продукции, производимой в нескольких пунктах производства [1, 3, 7]. В общем виде задача может быть сформулирована следующим образом. Однородный продукт, сосредоточенный в  пунктах производства, необходимо распределить между  пунктами потребления. Стоимость перевозки единицы продукции известна для всех маршрутов. Необходимо составить такой план перевозок, при котором запросы всех пунктов потребления были бы удовлетворены за счет имеющихся продуктов в пунктах производства и общие транспортные расходы по доставке продуктов были бы минимальными.Примем следующие обозначения: i – номер пункта производства, j –номер пункта потребления, 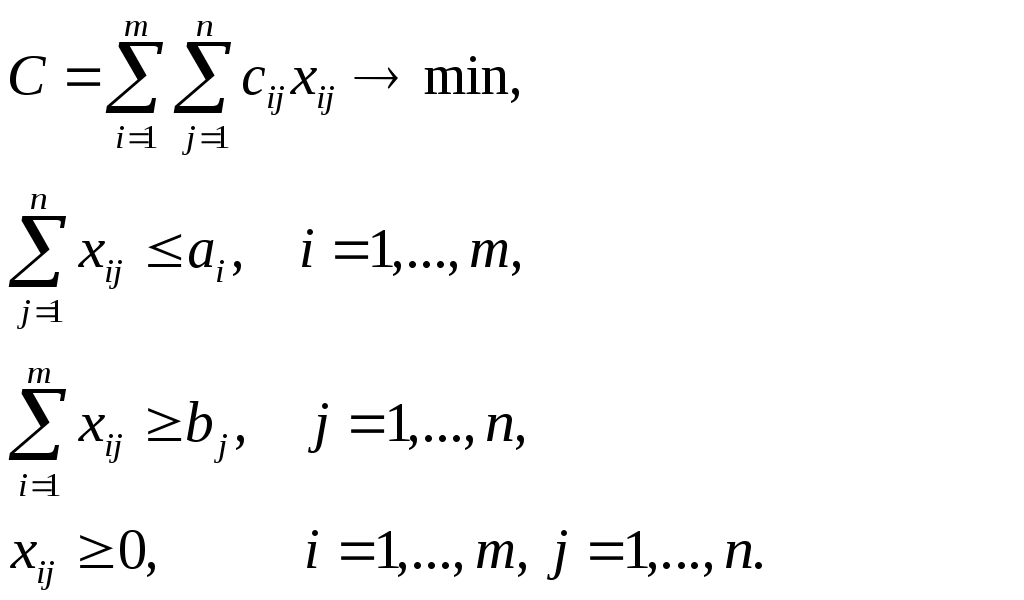 – количество продукта, имеющееся в i-ом пункте производства,  – количество продукта, необходимое для j-го пункта потребления,  – стоимость перевозки единицы продукта из i-го пункта производства в j-й пункт потребления,  – количество груза, планируемого к перевозке из i-го пункта производства в j-й пункт потребления, i=1,2,…,m; j=1,2,…,n. Математическая модель транспортной задачи будет выглядеть следующим образом: Условия задачи удобно записывать в виде таблицы, которая называется матрицей планирования:
Рассмотрим решение транспортной задачи в табличном процессоре MS Excel. Так как транспортная задача является частным случаем задачи линейного программирования, то эту задачу можно решать так, как описано выше. Однако благодаря свойствам задачи, ее можно записать в более компактной форме. Рассмотрим транспортную задачу, матрица планирования которой имеет вид:
Для решения транспортной задачи введем данные, как показано на рис.6. 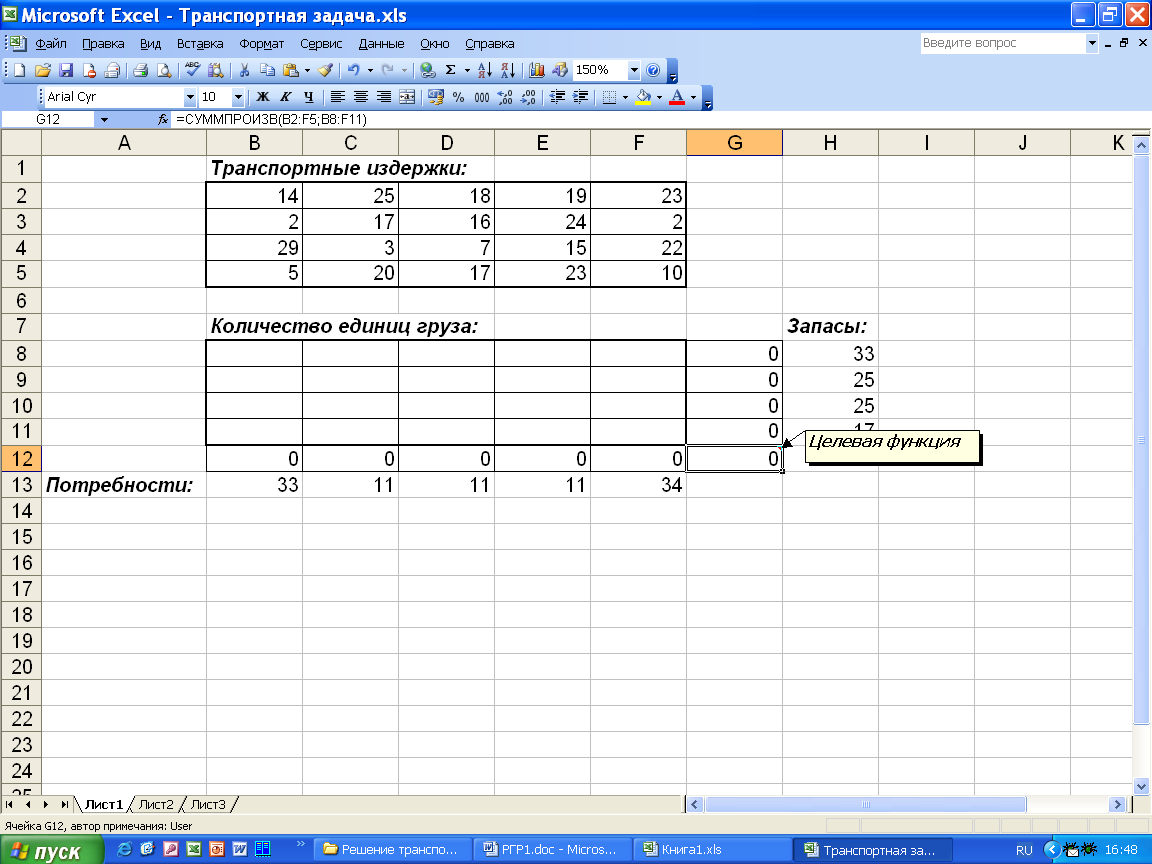 Рис.6. Исходные данные транспортной задачи. Вячейки B2 : F5 введем стоимость перевозок. Ячейки B8 : F11 отведены под значения объемов перевозок, пока неизвестные. В ячейки H8 : H11 введены объемы производства, а в ячейки B13 : F13 - потребности (спрос) в продукции в пунктах потребления. В ячейку G12 вводится целевая функция = СУММПРОИЗВ (B2 : F5; B8 : F11) . В ячейки B12 : F12 вводятся формулы = СУММ (B8 : B11), = СУММ (C8 : C11), = СУММ (D8 : D11), = СУММ (E8 : E11), = СУММ (F8 : F11), определяющие объем продукции, ввозимой в пункты потребления. В ячейки G8 : G11 введены формулы = СУММ (B8 : F8), = СУММ (B9 : F9), = СУММ (B10 : F10), = СУММ (B11 : F11), характеризующие объем продукции, вывозимой из пунктов производства. Далее выбираем команду Сервис, Поиск решения и заполняем открывшееся диалоговое окно Поиск решения, как показано на рис.7. 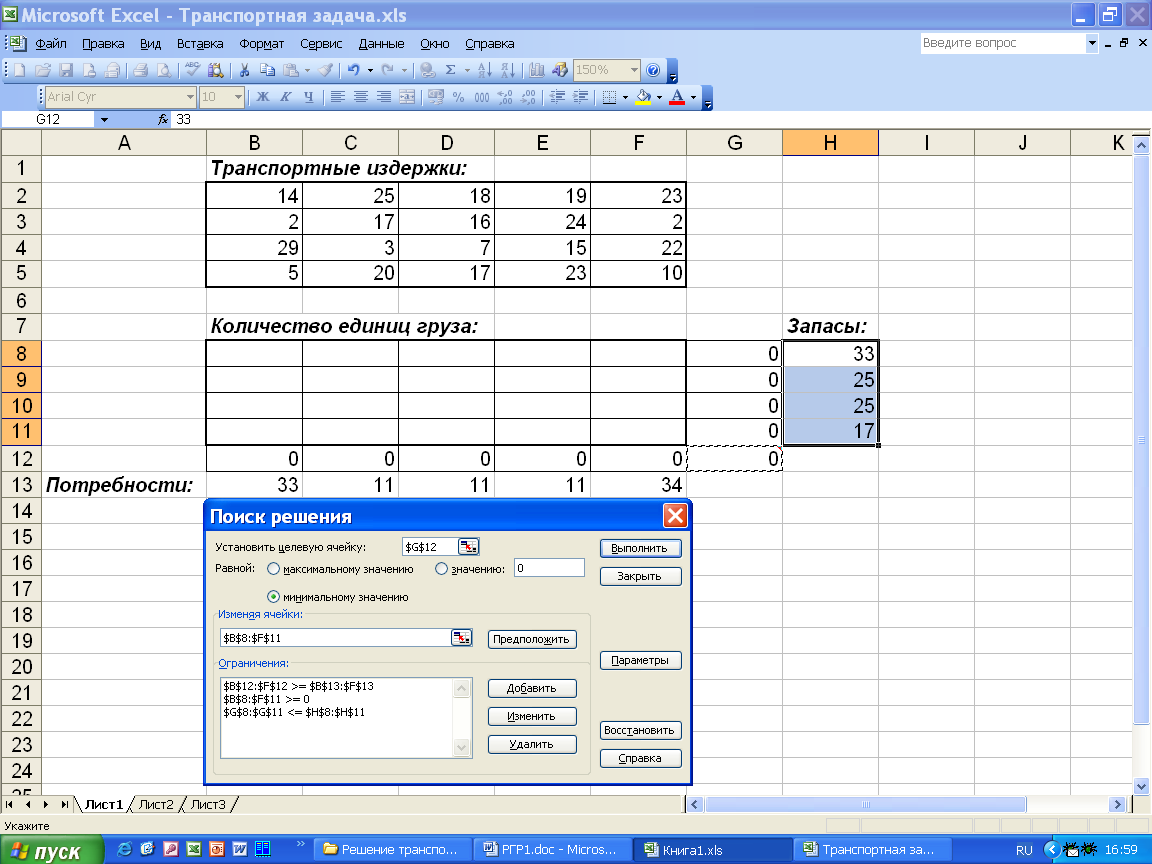 Рис.7. Диалоговое окно Поиск решения для транспортной задачи. В диалоговом окне Параметры поиска решения установить флажок Линейная модель (рис.8). 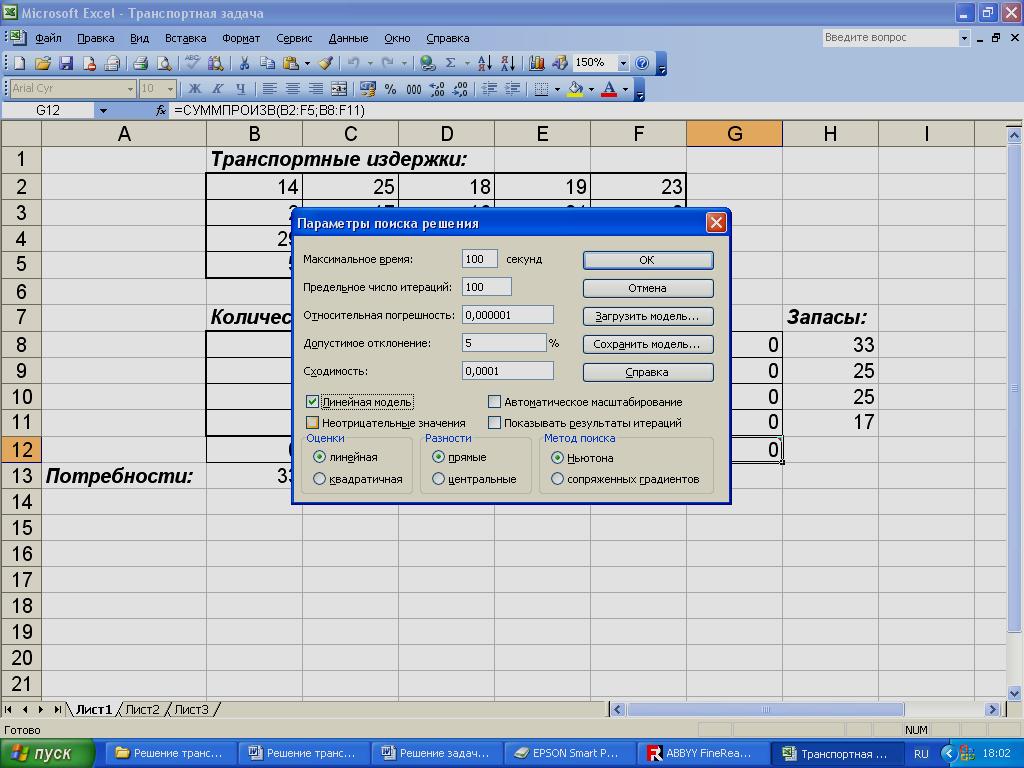 Рис.8. Диалоговое окно Параметры поиска решений. После нажатия кнопки Выполнить получаем оптимальный план поставок продукции и соответствующие ему транспортные расходы (рис. 9). 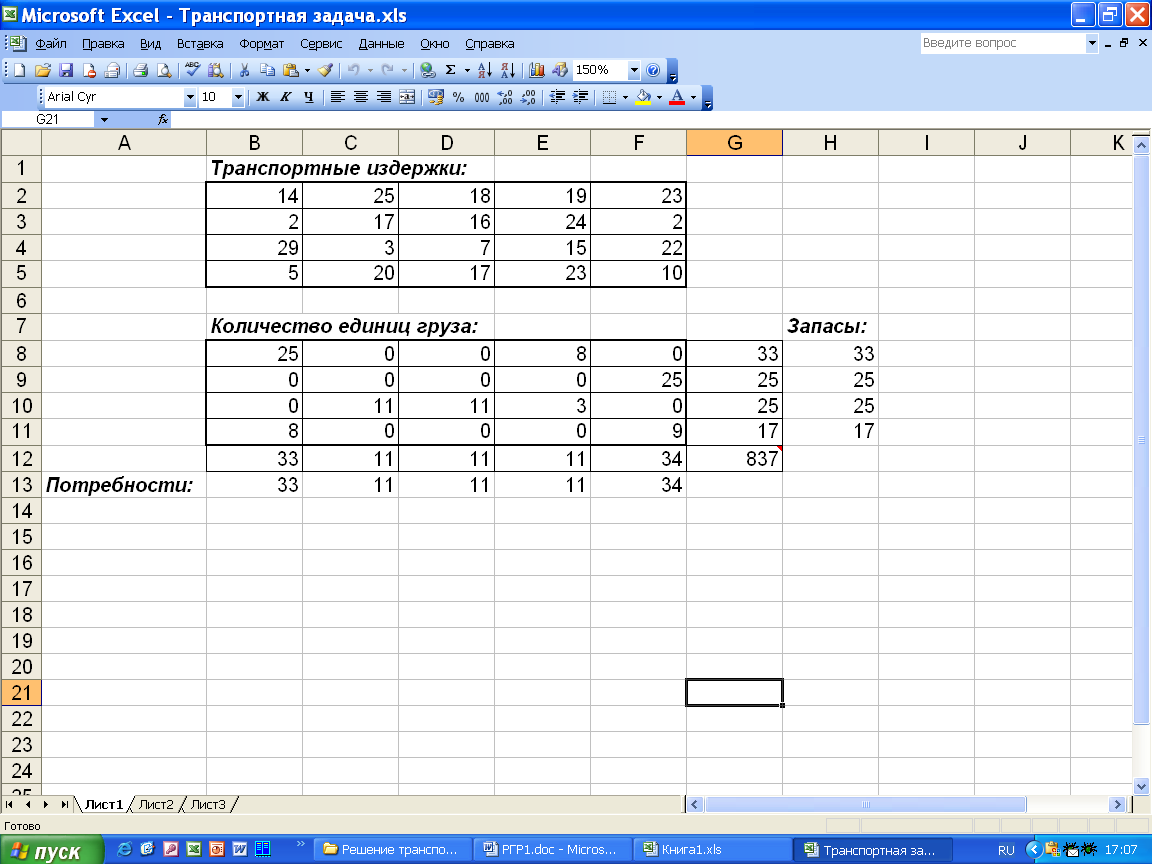 Рис.9. Оптимальное решение транспортной задачи. |