Решение задач математической физики численными методами
 Скачать 0.93 Mb. Скачать 0.93 Mb.
|
ФАКУЛЬТЕТ Фундаментальные науки КАФЕДРА Высшая математика РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К КУРСОВОЙ РАБОТЕ НА ТЕМУ: Решение задач математической физики численными методами Студент ФН1-61Б _________________ Е.М.Иванова (Группа) (Подпись, дата) (И.О.Фамилия) Руководитель курсовой работы _________________ А.А.Федотов (Подпись, дата) (И.О.Фамилия) Консультант _________________ П.В.Храпов (Подпись, дата) (И.О.Фамилия) 2020 г. Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Московский государственный технический университет имени Н.Э. Баумана (национальный исследовательский университет)» (МГТУ им. Н.Э. Баумана) УТВЕРЖДАЮ Заведующий кафедрой __________ (Индекс) ______________ _______________ (И.О.Фамилия) « _____ » ____________ 20 ____ г. ЗАДАНИЕ на выполнение курсовой работы по дисциплине Методы вычислений Студент группы ФН1-61Б Иванова Елена Михайловна (Фамилия, имя, отчество) Тема курсовой работы: Решение задач математической физики численными методами Направленность КР (учебная, исследовательская, практическая, производственная, др.) Учебная, исследовательская Источник тематики (кафедра, предприятие, НИР) ФН1 График выполнения работы: 25% к 3 нед., 50% к 9 нед., 75% к 12 нед., 100% к 15 нед. Задание Решить смешанную задачу для двумерного волнового уравнения методом конечных элементов Оформление курсовой работы: Расчетно-пояснительная записка на _____ листах формата А4. _______________________________________________________________________________ _______________________________________________________________________________ _______________________________________________________________________________ _______________________________________________________________________________ Дата выдачи задания « 7 » февраля 2020 г. Руководитель курсовой работы _________________ А.А.Федотов (Подпись, дата) (И.О.Фамилия) Студент _________________ Е.М.Иванова (Подпись, дата) (И.О.Фамилия) Примечание: Задание оформляется в двух экземплярах: один выдается студенту, второй хранится на кафедре. ОГЛАВЛЕНИЕ 1.Решение смешанной задачи для нестационарного двумерного уравнения теплопроводности методом конечных элементов. 4 1.1 Постановка задачи. 4 Найти решение смешанной задачи для гиперболического уравнения 4 (1) 4 1.2 Задание 5 1.1.Постановка задачи 11 1.2.Задание 12 Список использованных источников 19 1.2 Листинг кода graphik_ver_1……………………..........................................................................25 Введение. В настоящей работе была решена смешанная задача для двумерного волнового уравнения методом конечных элементов (так называемая тестовая задача), а также начально-краевая задача для нестационарного двумерного уравнения теплопроводности (задача курсовой работы). Были получены графики решения обеих задач в двумерном и трёхмерном виде, а также графики решений в сечениях при x=0 и y=0. Метод конечных элементов (МКЭ) – это метод приближённого численного решения физических задач. Историческими предшественниками МКЭ были различные методы строительной механики и механики деформируемого твёрдого тела, использующие дискретизацию. МКЭ может быть охарактеризован следующими свойствами: Физическая область задачи делится на подобласти, или конечные элементы. Зависимая переменная (одна или несколько) аппроксимируется функцией специального вида на каждом конечном элементе и, следовательно, во всей области. Параметры этих аппроксимаций в последующем становятся неизвестными параметрами задачи. Подстановка аппроксимаций в определяющие уравнения (или эквивалентные им) даёт систему множества уравнений с неизвестными параметрами. Решая эти уравнения, можно определить значения этих параметров, и, следовательно, получить приближённое решение задачи. Являясь одним из универсальных методов, МКЭ находит различное применение в широком спектре задач математического моделирования в механике и физике, а также применяется в программных комплексах для нелинейного динамического анализа, помогая решить многие проблемы в области проектирования прочных и легких конструкций, модификации уже выпускающихся изделий. Яркий пример использования МКЭ – это его применение для некоторые расчётов в советском крылатом орбитальном корабле многоразового использования «Буран». Для получения минимальной массы конструкции планера и его элементов были использованы программы ЦАГИ (Центральный Аэрогидродинамический институт им. проф. Н. Е. Жуковского), реализующие метод конечных элементов. Проведенные численные исследования позволили решить принципиальные вопросы определения напряженного и деформированного состояния конструкций деформации фюзеляжа и створок ОПГ (отсек полезного груза) при различных условиях нагружения, напряженного состояния конструкции при воздействии сосредоточенных нагрузок, деформации и температурных нагрузок, вызываемых неравномерным нагревом или различными коэффициентами линейного расширения материалов, и т.п. Решение смешанной задачи для нестационарного двумерного уравнения теплопроводности методом конечных элементов. 1.1 Постановка задачи. Найти решение 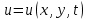 смешанной задачи для гиперболического уравнения смешанной задачи для гиперболического уравнения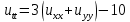 (1) (1)в области S (рис.2) при t[0,5], удовлетворяющее начальным условиям 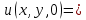 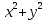 , , 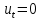 , , 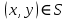 (2) (2)и граничным условиям 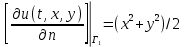 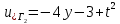 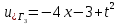 (3) (3)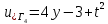 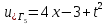 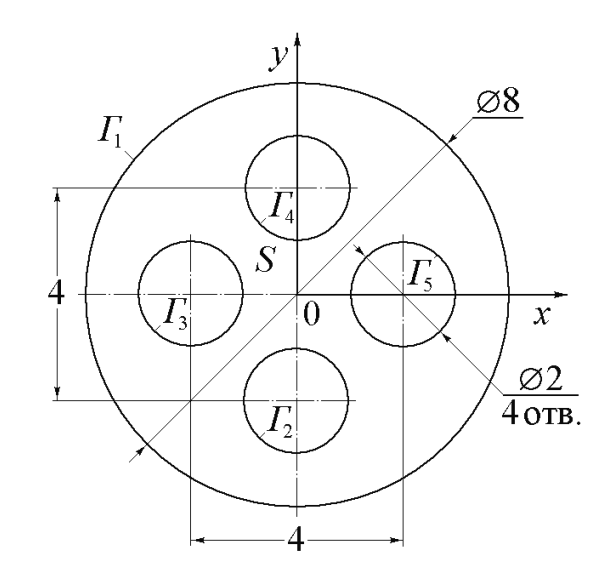 Рис. 2 Точное решение: 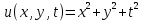 1.2 Задание Сформулировать постановку задачи, имеющей аналитическое решение 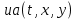 . Проверить, что функция . Проверить, что функция 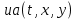 удовлетворяет уравнению (1.1), начальному условию (1.2) и граничным условиям (1.3). Провести методические расчеты для выбора расчетной сетки, сравнить аналитическое решение с численным при удовлетворяет уравнению (1.1), начальному условию (1.2) и граничным условиям (1.3). Провести методические расчеты для выбора расчетной сетки, сравнить аналитическое решение с численным при 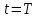 в сечениях в сечениях 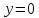 и и 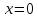 . Вывести результаты в текстовые файлы в виде таблиц . Вывести результаты в текстовые файлы в виде таблиц 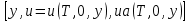 и и 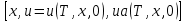 . .Используя метод конечных элементов, найти решение смешанной задачи. Построить поверхность 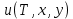 , графики , графики 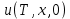 , , 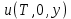 . .Численное решение. Сначала рисуется расчетная область S, изображённая на рисунке 2. После этого задаются уравнение (1) и граничные условия (3), которые предварительно нужно записать в стандартном виде, используемом в среде PDETool: 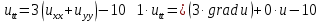 , ,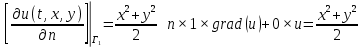 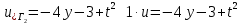 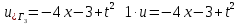 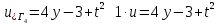 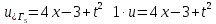 На следующем шаге в области S c помощью пункта меню Mesh формируется конечно-элементная сетка. Затем в окне Solve Parameters задаются начальные условия и отрезок времени, на котором строится решение рассматриваемой задачи. В этом же окне можно установить допустимый уровень относительной (Relative tolerance) и абсолютной (Absolute tolerance) погрешности решения задачи. 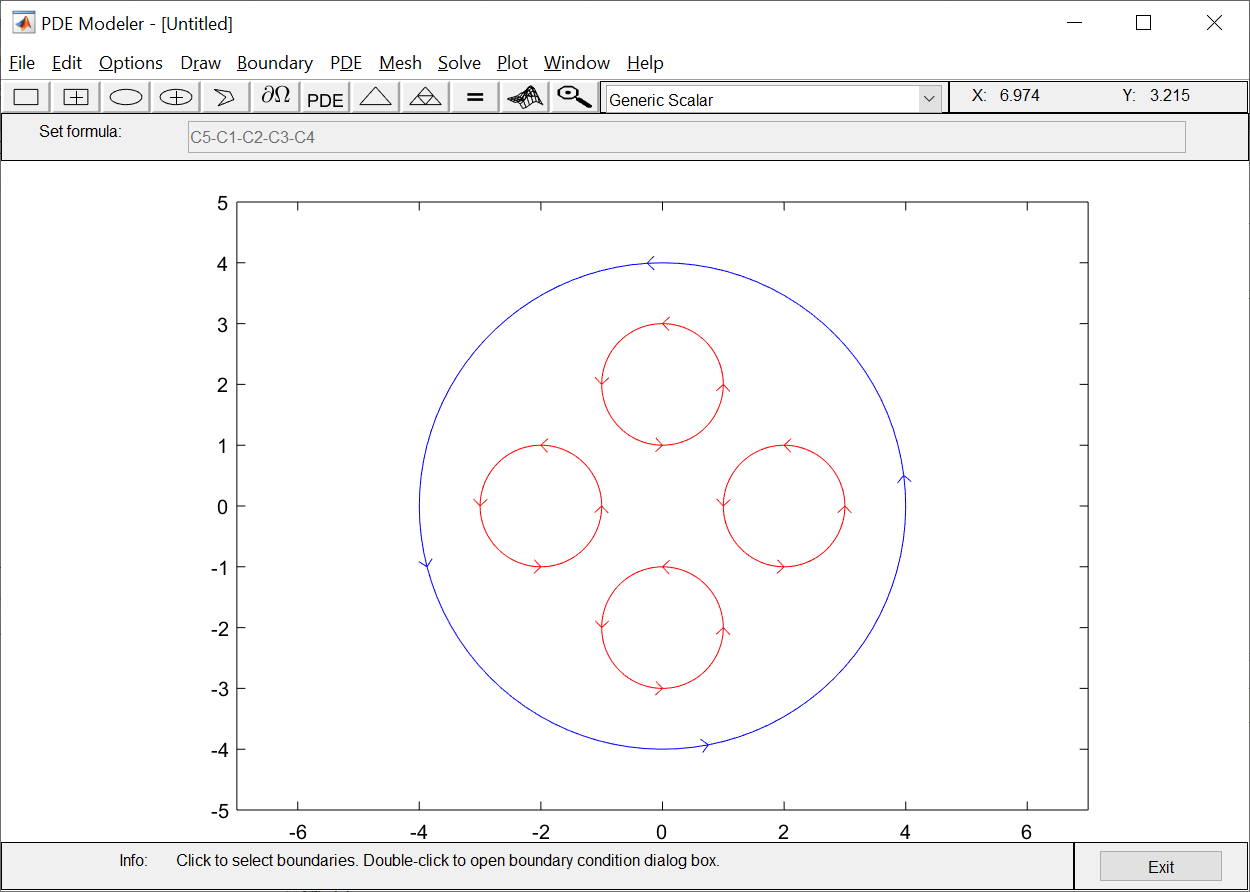 Нарисованная в PDE Modeler область S. 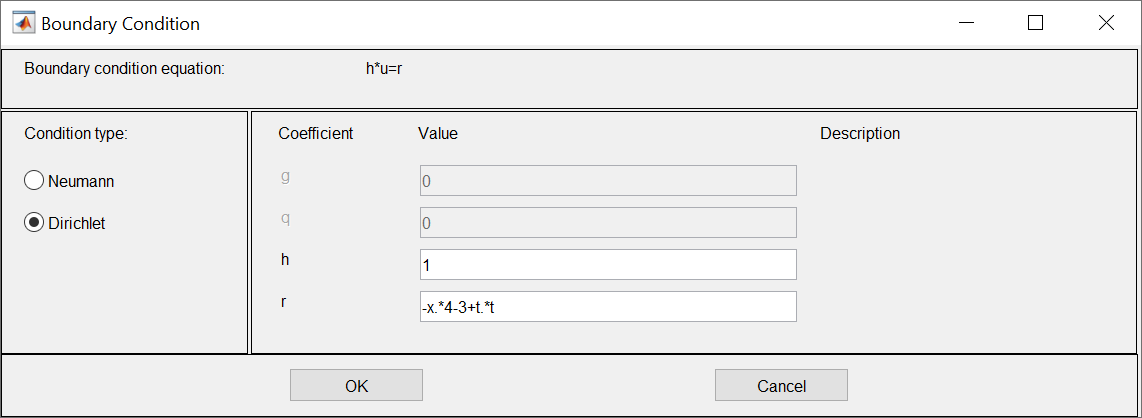 Пример граничных условий Дирихле на границе Г3. 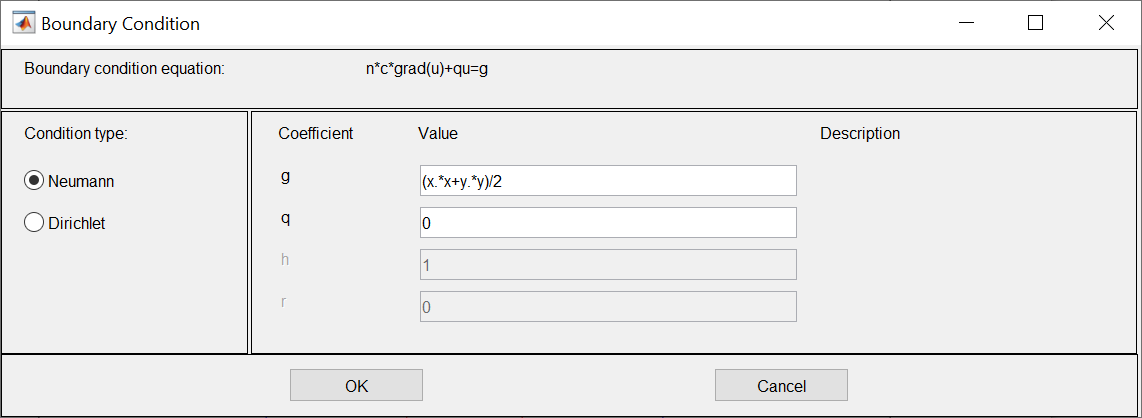 Пример граничных условий Неймана на границе Г1. 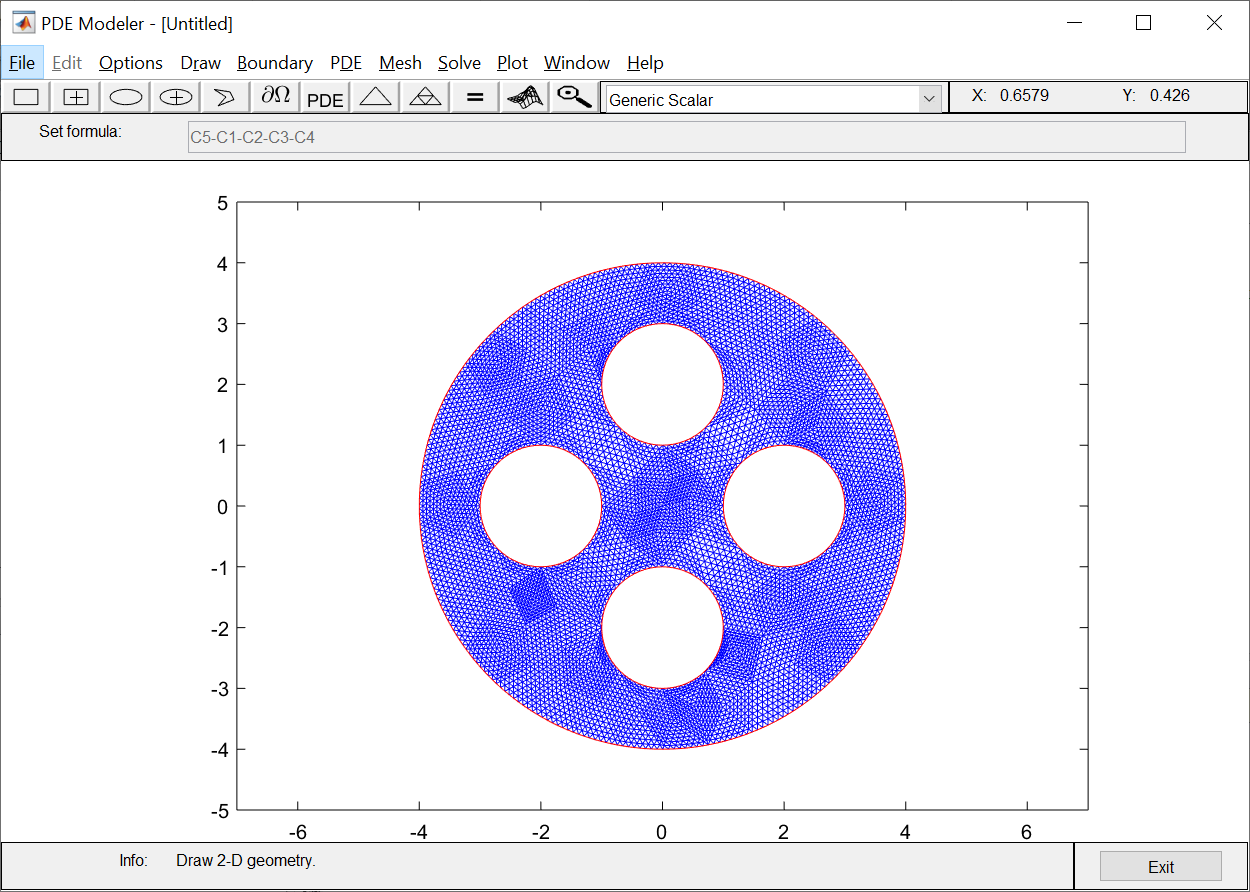 Пример формирования конечно-элементной сетки. 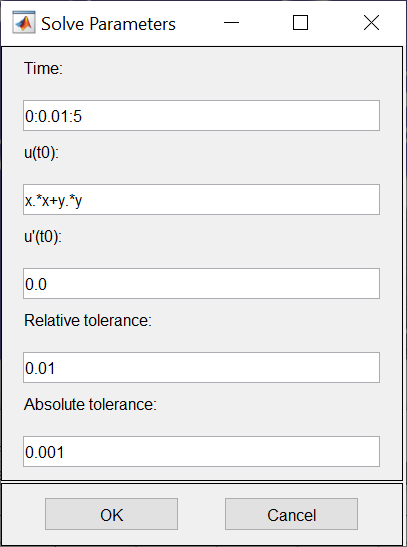 Окно Solve Parameters. Второе и третье вводимые строки - начальные условия, первая вводимая строка - отрезок времени, на котором строится решение рассматриваемой задачи. Четвёртая вводимая строка - допустимый уровень относительной (Relative tolerance) погрешности. Пятая строка - абсолютная (Absolute tolerance) погрешности решения задачи.  1.4 Далее с помощью пункта меню «Solve» «Solve PDE» получаем решение задачи: 1.4 Далее с помощью пункта меню «Solve» «Solve PDE» получаем решение задачи: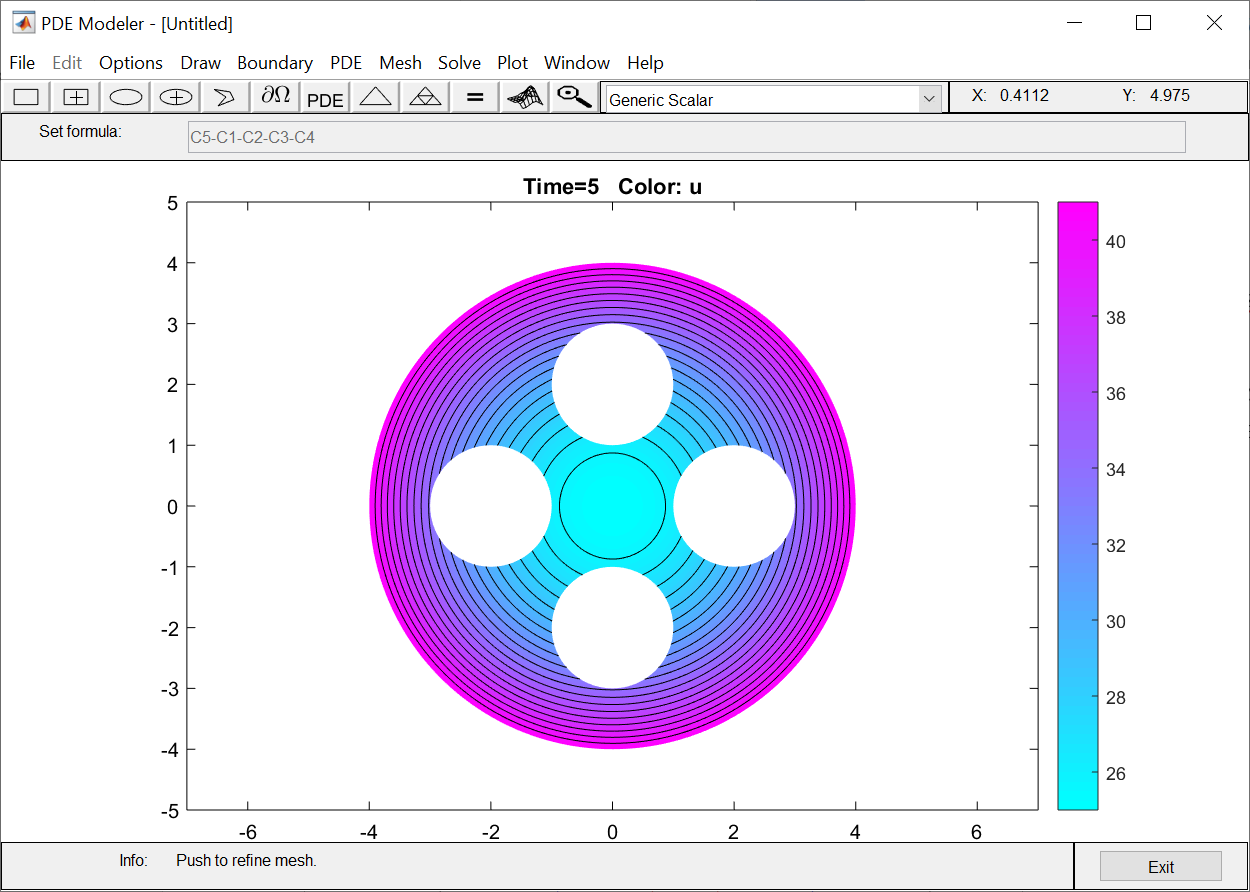 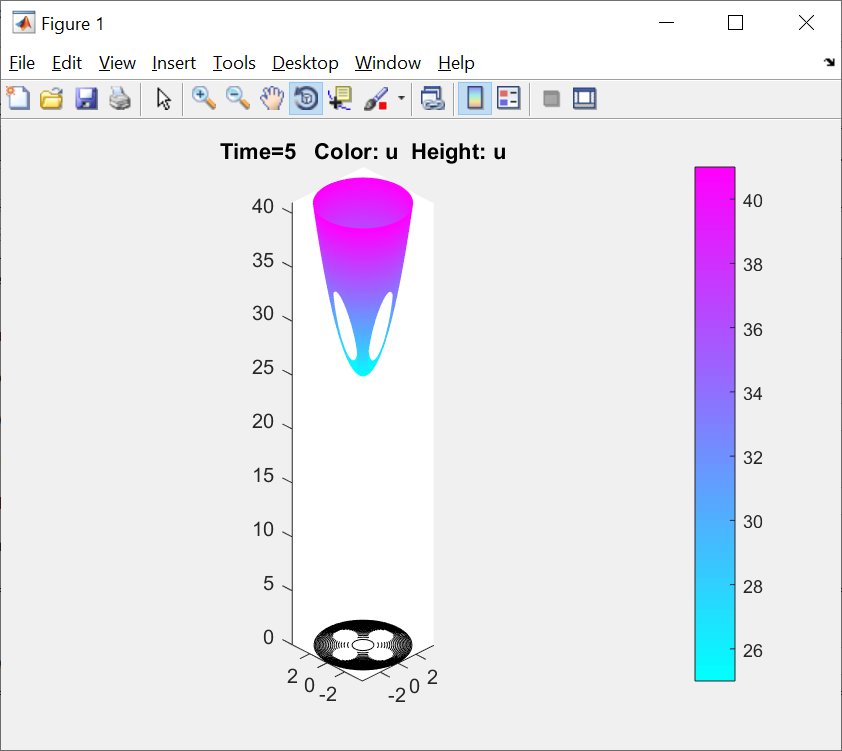 2-D и 3-D изображения решений соответственно. Также с помощью отдельного m-файла «graphik_ver_1» получаем решения задачи в сечениях при x=0 и y=0: 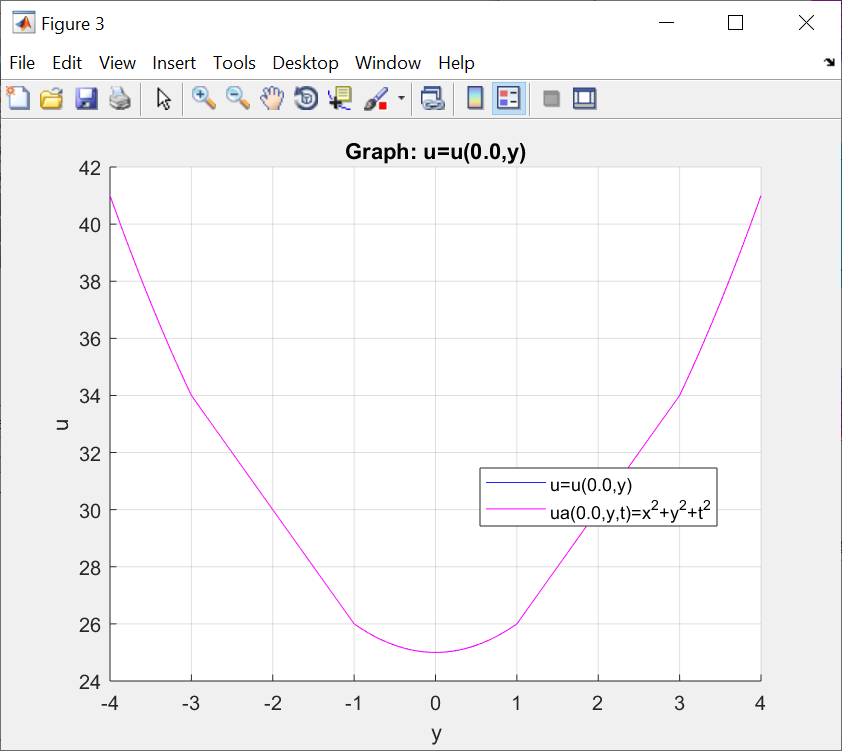 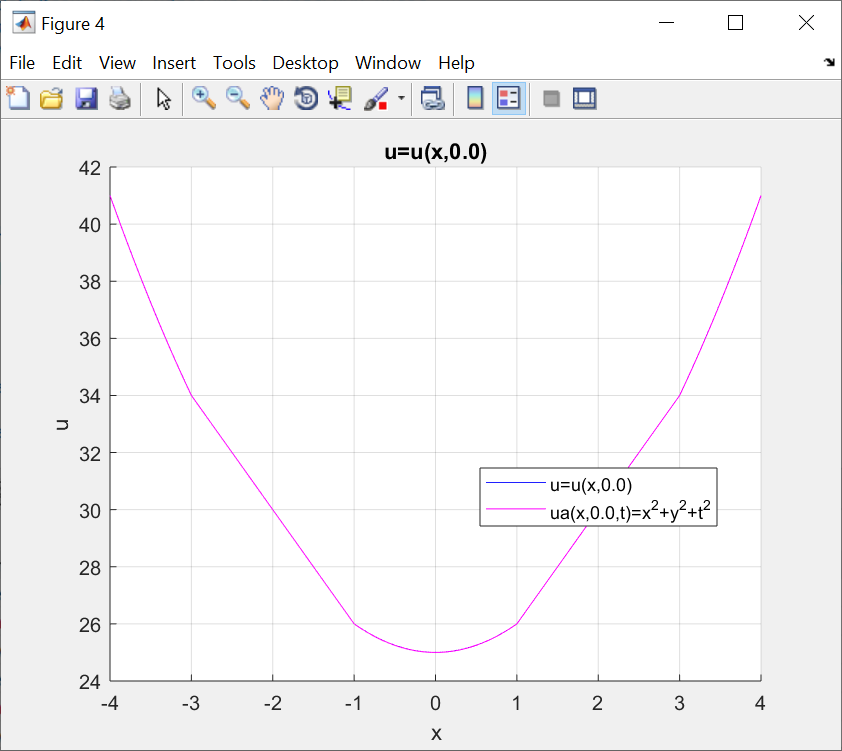 Начально-краевая задача для нестационарного двумерного уравнения теплопроводности Постановка задачи Найти функцию 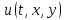 в области в области 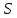 (Рис. 1), удовлетворяющую уравнению (Рис. 1), удовлетворяющую уравнению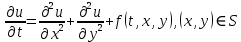 , (1.1) , (1.1) начальному условию 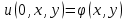 , (1.2) , (1.2) и граничным условиям 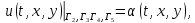 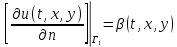 (1.3) (1.3) Где 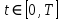 , , 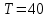 , ,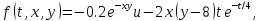 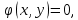 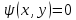 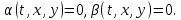  Рис. 1 Задание Сформулировать постановку задачи, имеющей аналитическое решение 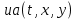 . Проверить, что функция . Проверить, что функция 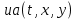 удовлетворяет уравнению (1.1), начальному условию (1.2) и граничным условиям (1.3). Провести методические расчеты для выбора расчетной сетки, сравнить аналитическое решение с численным при удовлетворяет уравнению (1.1), начальному условию (1.2) и граничным условиям (1.3). Провести методические расчеты для выбора расчетной сетки, сравнить аналитическое решение с численным при 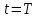 в сечениях в сечениях 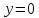 и и 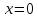 . Вывести результаты в текстовые файлы в виде таблиц . Вывести результаты в текстовые файлы в виде таблиц 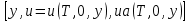 и и 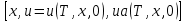 . .Используя метод конечных элементов, найти решение смешанной задачи. Построить поверхность 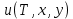 , графики , графики 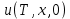 , , 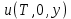 . .1.3 Численное решение. Решаем задачу аналогично тестовой задаче. Сначала рисуем расчетную область S, изображённая на рисунке 1. После этого задаём уравнение (1.1) и граничные условия (1.3), которые предварительно нужно записать в стандартном виде, используемом в среде PDETool: 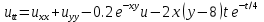 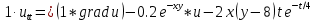 , ,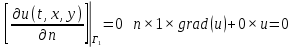 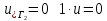 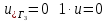 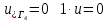 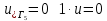 На следующем шаге в области S c помощью пункта меню Mesh формируется конечно-элементная сетка. Затем в окне Solve Parameters задаются начальные условия и отрезок времени, на котором строится решение рассматриваемой задачи. В этом же окне можно установить допустимый уровень относительной (Relative tolerance) и абсолютной (Absolute tolerance) погрешности решения задачи. Рисуем область S (рис. 1), задаем уравнение (1.1) и граничные условия (1.3), c помощью пункта меню Mesh формируем конечно-элементную сетку. Затем в окне Solve Parameters задаём начальные условия (1.2) и отрезок времени, на котором строится решение рассматриваемой задачи. В этом же окне указываем относительную (Relative tolerance) и абсолютную (Absolute tolerance) погрешности решения задачи.  Нарисованная в PDE Modeler область S. 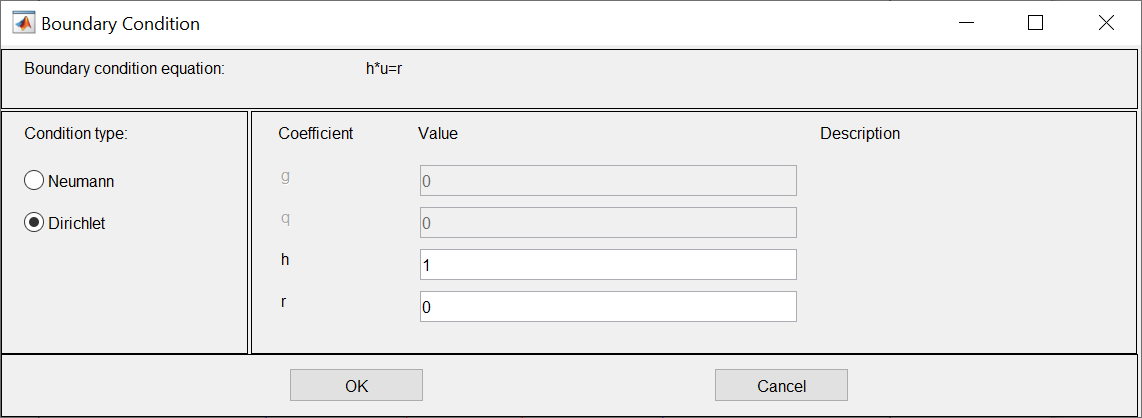 Пример граничных условий Дирихле на границе Г3. 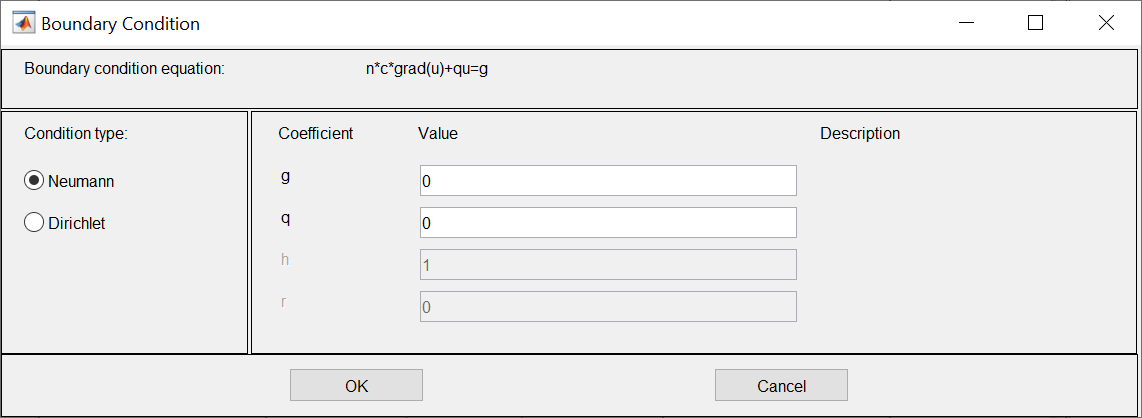 Пример граничных условий Неймана на границе Г1.  Пример формирования конечно-элементной сетки. 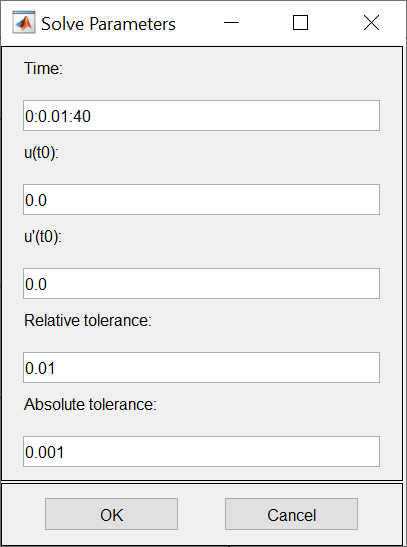 Окно Solve Parameters. Второе и третье вводимые строки - начальные условия, первая вводимая строка - отрезок времени, на котором строится решение рассматриваемой задачи. Четвёртая вводимая строка - допустимый уровень относительной (Relative tolerance) погрешности. Пятая строка - абсолютная (Absolute tolerance) погрешности решения задачи.  1.4 Далее с помощью пункта меню «Solve» «Solve PDE» получаем решение задачи: 1.4 Далее с помощью пункта меню «Solve» «Solve PDE» получаем решение задачи: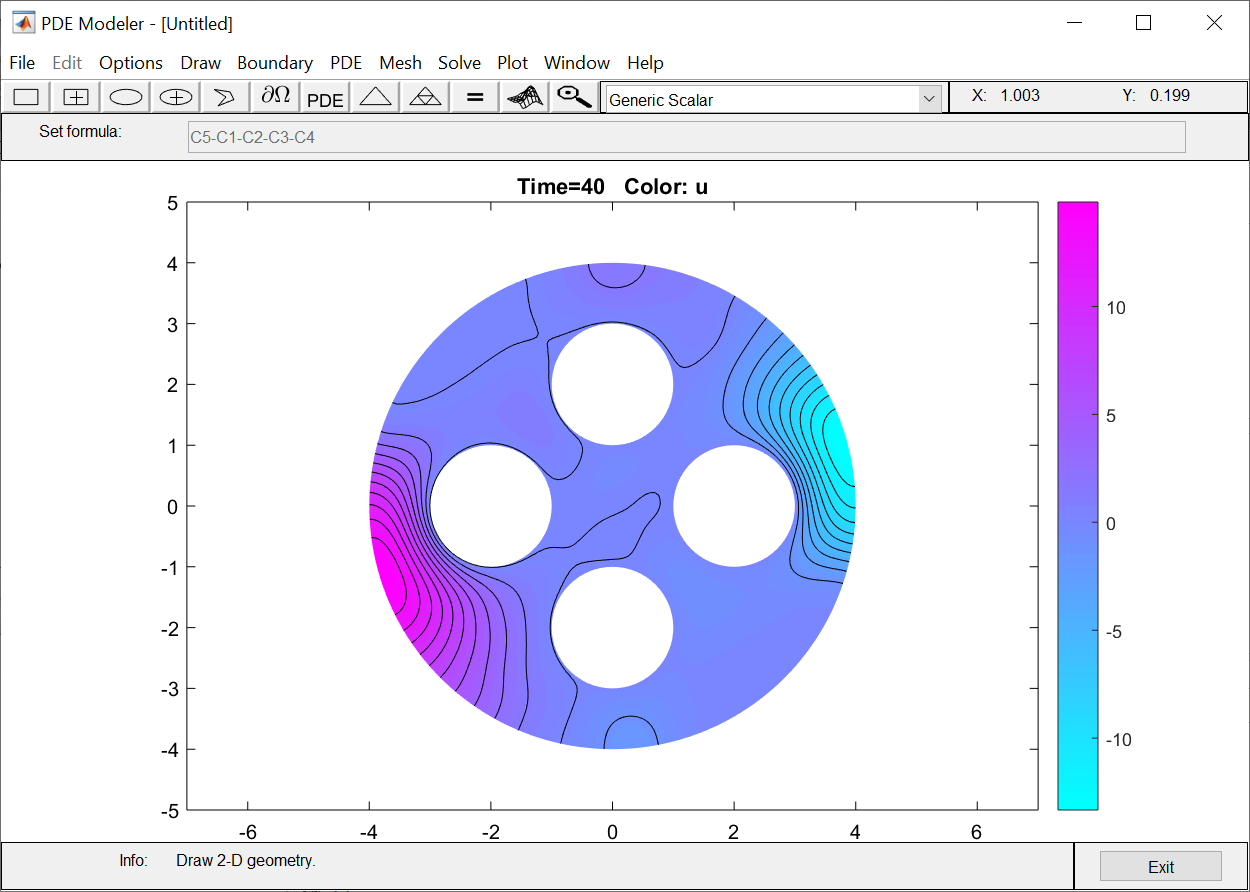 2-D решение задачи. 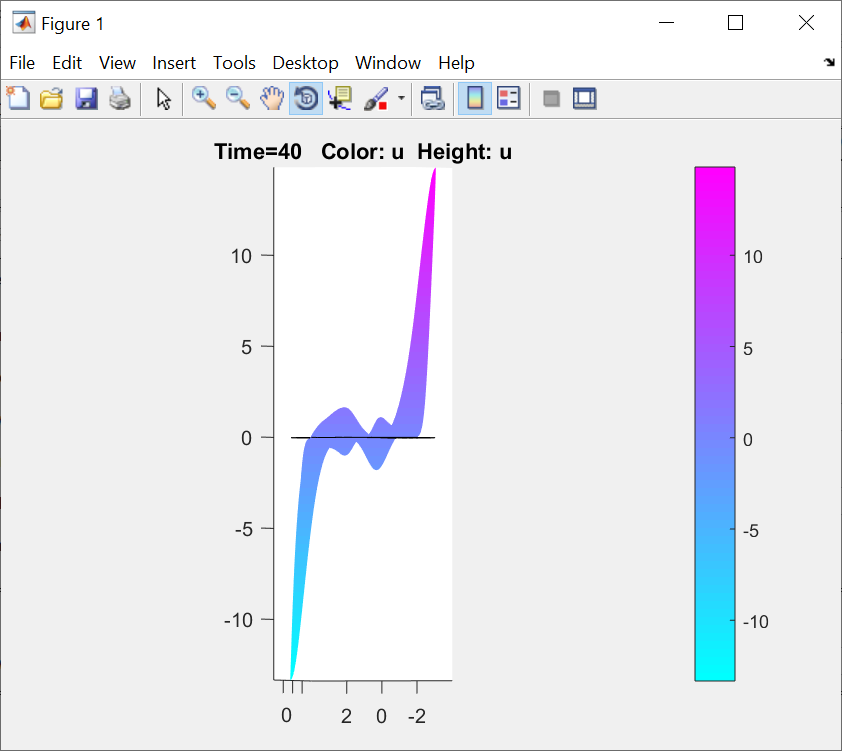 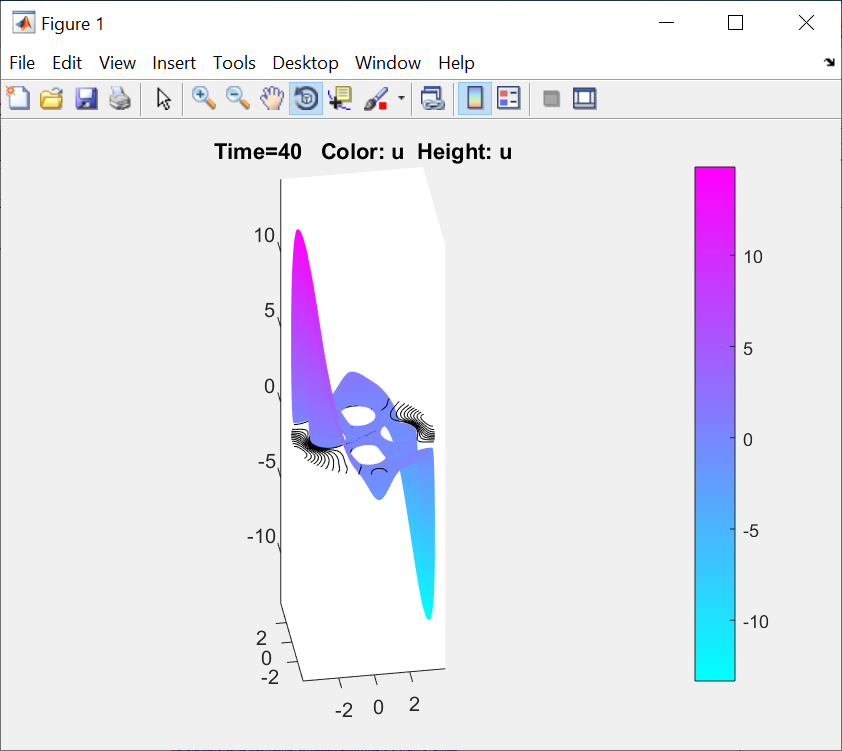 3-D изображение решения задачи. (оба рисунка) Также с помощью отдельного m-файла «graphik_ver_1» получаем решения задачи в сечениях при x=0 и y=0: 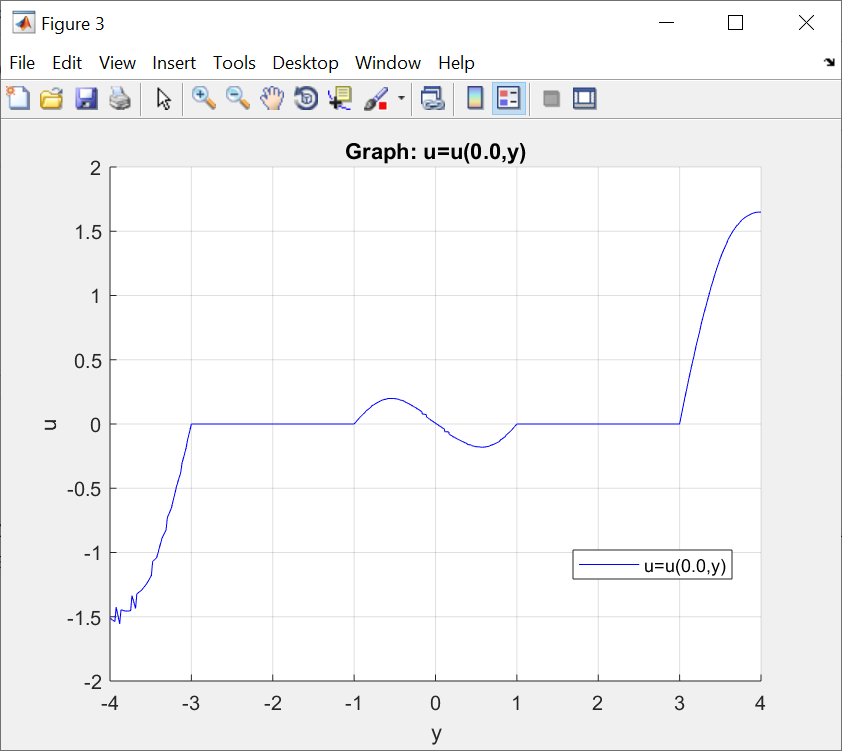 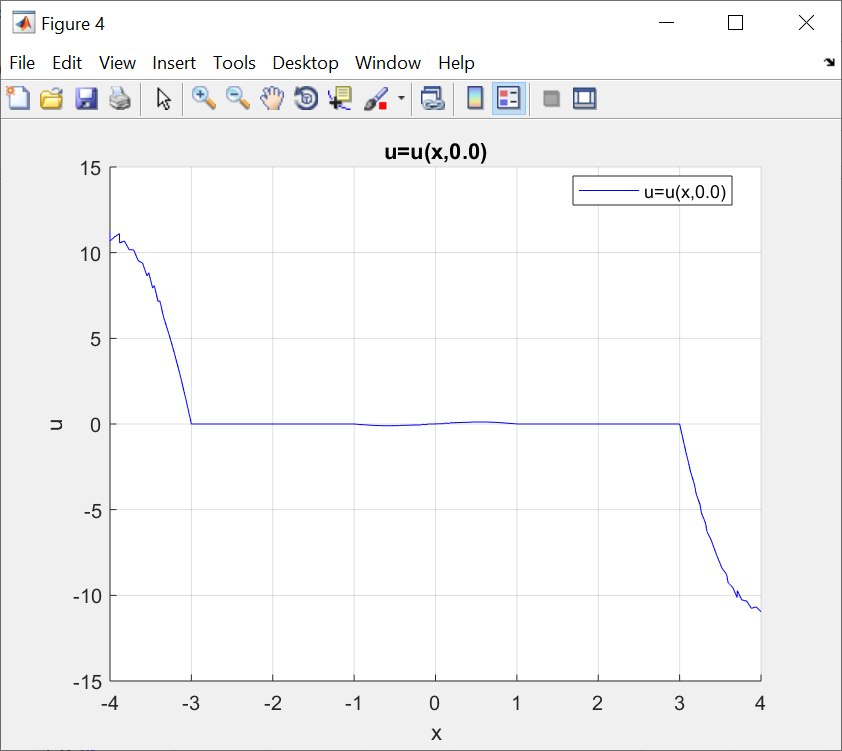 Заключение. Таким образом, метод конечных элементов является универсальным средством для решения задач математической физики. Набор инструментов «PDETool» пакета прикладных программ «MATLAB» охватывает достаточно широкий спектр задач, среди которых: плоская задача теории упругости, стационарная и нестационарная задачи инженерных и научных расчетов теплопроводности и диффузии, задачи электростатики и магнитостатики. Кроме того, имеется возможность задания эллиптических, параболических и гиперболических уравнений и систем, решения задач на собственные значения и задач, описываемых нелинейными дифференциальными уравнениями. Применение этого набора инструментов упрощает вычисления и позволяет получить решение задачи с достаточной точностью в удобном для пользователя виде. Приведенные примеры расчётов задач в курсовой работе позволяют сделать вывод о том, что среда PDE Toolbox может оказаться весьма удобной для численного решения задач механики, в частности различных задач теплопроводности и прочности, задач деформации, неравномерного нагрева и нагружения частей механических конструкций, устойчивости элементов сооружений к различным воздействиям. Благодаря набору готовых функций и возможности изучать и развивать реализованные в них алгоритмы «PDETool» с встроенным в него методом конечных элементов является одним из мощных инструментов вычисления. Список использованных источников 1. Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.: Наука, 2004. – 798 с. 2. Формалев В.Ф., Ревизников Д.Л. Численные методы. – М.: Физматлит, 2004. – 400 с. 3. Самарский А.А., Гулин А.В. Численные методы математической физики. – М.: Научный мир, 2000. – 315 с. 4. Численные методы. Учебник в 2 книгах. Книга 1. Численный анализ. Калиткин Н. Н., Альшина Е. А., 304 с.; Книга 2. Методы математической физики. Калиткин Н. Н., Корякин П.В. – М.: 2013.: Academia , 304 с. 5. Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1989.- 432с. 6. Амосов А. А., Дубинский Ю. А., Копченова Н. В. Вычислительные методы. СПб.: Лань, 2014. – 672 с. 7. Шмелев В.Е. MatLab. Partial Differential Equations Toolbox, 2015. 8. Норри Д., де Фриз Ж. Введение в метод конечных элементов. – М.: Мир, 1981. – 304 с. (Перевод с английского. D.H. Norrie and G. de Vries. An Introduction to Finite Element Analysis. New York, San Francisco, London: Academic Press, 1978.). 9. Мэтьюз Д.Г., Финк К.Д. Численные методы. Использование MATLAB. 3-е издание.: Пер. с англ. – М.: Издательский дом «Вильямс», 2001. Приложение 1. 1.1 Листинг кода kursv1_ver_1 function kursv1_ver_1 [pde_fig,ax]=pdeinit; pdetool('appl_cb',1); set(ax,'DataAspectRatio',[1 1 1]); set(ax,'PlotBoxAspectRatio',[7 5 1]); set(ax,'XLim',[-7 7]); set(ax,'YLim',[-5 5]); set(ax,'XTickMode','auto'); set(ax,'YTickMode','auto'); % Geometry description: pdecirc(0,2,1,'C1'); pdecirc(0,-2,1,'C2'); pdecirc(2,0,1,'C3'); pdecirc(-2,0,1,'C4'); pdecirc(0,0,4,'C5'); set(findobj(get(pde_fig,'Children'),'Tag','PDEEval'),'String','C5-C1-C2-C3-C4') % Boundary conditions: pdetool('changemode',0) pdesetbd(20,... 'neu',... 1,... '0',... '(x.*x+y.*y)/2') pdesetbd(19,... 'neu',... 1,... '0',... '(x.*x+y.*y)/2') pdesetbd(18,... 'neu',... 1,... '0',... '(x.*x+y.*y)/2') pdesetbd(17,... 'neu',... 1,... '0',... '(x.*x+y.*y)/2') pdesetbd(16,... 'dir',... 1,... '1',... '-x.*4-3+t.*t') pdesetbd(15,... 'dir',... 1,... '1',... '-x.*4-3+t.*t') pdesetbd(14,... 'dir',... 1,... '1',... '-x.*4-3+t.*t') pdesetbd(13,... 'dir',... 1,... '1',... '-x.*4-3+t.*t') pdesetbd(12,... 'dir',... 1,... '1',... 'x.*4-3+t.*t') pdesetbd(11,... 'dir',... 1,... '1',... 'x.*4-3+t.*t') pdesetbd(10,... 'dir',... 1,... '1',... 'x.*4-3+t.*t') pdesetbd(9,... 'dir',... 1,... '1',... 'x.*4-3+t.*t') pdesetbd(8,... 'dir',... 1,... '1',... '-y.*4-3+t.*t') pdesetbd(7,... 'dir',... 1,... '1',... '-y.*4-3+t.*t') pdesetbd(6,... 'dir',... 1,... '1',... '-y.*4-3+t.*t') pdesetbd(5,... 'dir',... 1,... '1',... '-y.*4-3+t.*t') pdesetbd(4,... 'dir',... 1,... '1',... 'y.*4-3+t.*t') pdesetbd(3,... 'dir',... 1,... '1',... 'y.*4-3+t.*t') pdesetbd(2,... 'dir',... 1,... '1',... 'y.*4-3+t.*t') pdesetbd(1,... 'dir',... 1,... '1',... 'y.*4-3+t.*t') % Mesh generation: setappdata(pde_fig,'Hgrad',1.3); setappdata(pde_fig,'refinemethod','regular'); setappdata(pde_fig,'jiggle',char('on','mean','')); setappdata(pde_fig,'MesherVersion','preR2013a'); pdetool('initmesh') pdetool('refine') pdetool('refine') pdetool('refine') % PDE coefficients: pdeseteq(3,... '1.0',... '0.0',... '-2',... '1.0',... '0:0.01:5',... 'x.*x+y.*y',... '0.0',... '[0 100]') setappdata(pde_fig,'currparam',... ['1.0';... '0.0';... '-2 ';... '1.0']) % Solve parameters: setappdata(pde_fig,'solveparam',... char('0','19968','10','pdeadworst',... '0.5','longest','0','1E-4','','fixed','Inf')) % Plotflags and user data strings: setappdata(pde_fig,'plotflags',[1 1 1 1 1 1 1 1 0 0 0 501 1 1 0 0 0 1]); setappdata(pde_fig,'colstring',''); setappdata(pde_fig,'arrowstring',''); setappdata(pde_fig,'deformstring',''); setappdata(pde_fig,'heightstring',''); % Solve PDE: pdetool('solve') 1.2 Листинг кода graphik_ver_1 function graphik_ver_1 load('u.mat','u') u=u(:,size(u,2)); load('e.mat','e') load('p.mat','p') load('t.mat','t') function plot_along_x(p,u,y_val) nodes_along_x=abs(p(2,:)-y_val) <0.05; [y_values,ind]=sort(p(1,nodes_along_x)); L_mas=length(y_values); u_along_x=u(nodes_along_x); u_along_x=u_along_x(ind); [fl, mes]=fopen('mfile_x.doc', 'w'); %fl=fopen('mfile_x.doc', 'w'); for i=1:L_mas ya(i)=ua(y_values(i),0.0,5); R=ya(i)-u_along_x(i); %fprintf(1,'%10.5f %10.5f\n',y_values(i),u_along_x(i)); fprintf(fl,'x(%d)=%7.4f y=%10.4f ua=%10.4f R=%10.4f\n',... i,y_values(i),u_along_x(i),ya(i),R); end fclose(fl); figure; hold on plot(y_values,u_along_x,'-b'); plot(y_values,ya,'-m'); legend('u=u(x,0.0)','ua(x,0.0,t)=x^2+y^2+t^2','Location','Best'); title('u=u(x,0.0)'); xlabel('x'); ylabel('u'); grid; end function plot_along_y(p,u,x_val) nodes_along_y=abs(p(1,:)-x_val) < 0.05; [x_values,ind]=sort(p(2,nodes_along_y)); L_mas=length(x_values); u_along_y=u(nodes_along_y); u_along_y=u_along_y(ind); [fl, mes]=fopen('mfile_y.doc', 'w'); %fl=fopen('mfile.doc', 'w'); for i=1:L_mas ya(i)=ua(0.0,x_values(i),5); R=ya(i)-u_along_y(i); %fprintf(1,'%10.5f %10.5f\n',u_along_y(i),x_values(i)); % fprintf(fl,'%10.5f %10.5f\n',u_along_y(i),x_values(i)); fprintf(fl,'y(%d)=%7.4f y_ch=%10.4f ua=%10.4f R=%10.4f\n',... i,x_values(i),u_along_y(i),ya(i),R); end fclose(fl); figure; hold on plot(x_values, u_along_y,'-b'); plot(x_values,ya,'-m'); %legend('u=u(x,y), x=0.0','Location','NorthEast'); legend('u=u(0.0,y)','ua(0.0,y,t)=x^2+y^2+t^2','Location','Best') title('Graph: u=u(0.0,y)'); ylabel('u'); xlabel('y'); grid; end function [s]=ua(x,y,t) s=x.^2+y.^2+t.^2; end pdemesh(p,e,t); axis equal figure pdeplot(p,e,t,'xydata',u,'colormap','cool','colorbar','on','contour','on') % for j=1:5512 % x=p(1,j); % y=p(2,j); % fprintf(1,'j=%4d, x=%4.2f, y=%4.2f, u=%8.4f\n',j,x,y,u(j)) % end x_val=0.0; plot_along_y(p,u,x_val) y_val=0.0; plot_along_x(p,u,y_val) end Приложение 2. 1.1 Листинг кодаkursv1_ver_1 function kursv1_ver_1 [pde_fig,ax]=pdeinit; pdetool('appl_cb',1); set(ax,'DataAspectRatio',[1 1 1]); set(ax,'PlotBoxAspectRatio',[7 5 1]); set(ax,'XLim',[-7 7]); set(ax,'YLim',[-5 5]); set(ax,'XTickMode','auto'); set(ax,'YTickMode','auto'); % Geometry description: pdecirc(0,2,1,'C1'); pdecirc(0,-2,1,'C2'); pdecirc(2,0,1,'C3'); pdecirc(-2,0,1,'C4'); pdecirc(0,0,4,'C5'); set(findobj(get(pde_fig,'Children'),'Tag','PDEEval'),'String','C5-C1-C2-C3-C4') % Boundary conditions: pdetool('changemode',0) pdesetbd(20,... 'neu',... 1,... '0',... '0') pdesetbd(19,... 'neu',... 1,... '0',... '0') pdesetbd(18,... 'neu',... 1,... '0',... '0') pdesetbd(17,... 'neu',... 1,... '0',... '0') pdesetbd(16,... 'dir',... 1,... '1',... '0') pdesetbd(15,... 'dir',... 1,... '1',... '0') pdesetbd(14,... 'dir',... 1,... '1',... '0') pdesetbd(13,... 'dir',... 1,... '1',... '0') pdesetbd(12,... 'dir',... 1,... '1',... '0') pdesetbd(11,... 'dir',... 1,... '1',... '0') pdesetbd(10,... 'dir',... 1,... '1',... '0') pdesetbd(9,... 'dir',... 1,... '1',... '0') pdesetbd(8,... 'dir',... 1,... '1',... '0') pdesetbd(7,... 'dir',... 1,... '1',... '0') pdesetbd(6,... 'dir',... 1,... '1',... '0') pdesetbd(5,... 'dir',... 1,... '1',... '0') pdesetbd(4,... 'dir',... 1,... '1',... '0') pdesetbd(3,... 'dir',... 1,... '1',... '0') pdesetbd(2,... 'dir',... 1,... '1',... '0') pdesetbd(1,... 'dir',... 1,... '1',... '0') % Mesh generation: setappdata(pde_fig,'Hgrad',1.3); setappdata(pde_fig,'refinemethod','regular'); setappdata(pde_fig,'jiggle',char('on','mean','')); setappdata(pde_fig,'MesherVersion','preR2013a'); pdetool('initmesh') pdetool('refine') pdetool('refine') pdetool('refine') % PDE coefficients: pdeseteq(3,... '1.0',... '0.2*exp(-x.*y)',... '-2*x.*(y-8)*t.*exp(-t./4)',... '1.0',... '0:0.01:40',... '0.0',... '0.0',... '[0 100]') setappdata(pde_fig,'currparam',... ['1.0 ';... '0.2*exp(-x.*y) ';... '-2*x.*(y-8)*t.*exp(-t./4)';... '1.0 ']) % Solve parameters: setappdata(pde_fig,'solveparam',... char('0','19968','10','pdeadworst',... '0.5','longest','0','1E-4','','fixed','Inf')) % Plotflags and user data strings: setappdata(pde_fig,'plotflags',[1 1 1 1 1 1 1 1 0 0 0 4001 1 1 0 0 0 1]); setappdata(pde_fig,'colstring',''); setappdata(pde_fig,'arrowstring',''); setappdata(pde_fig,'deformstring',''); setappdata(pde_fig,'heightstring',''); % Solve PDE: pdetool('solve') 1.2 Листинг кода graphik_ver_1 function graphik_ver_1 load('u.mat','u') u=u(:,size(u,2)); load('e.mat','e') load('p.mat','p') load('t.mat','t') function plot_along_x(p,u,y_val) nodes_along_x=abs(p(2,:)-y_val) <0.05; [y_values,ind]=sort(p(1,nodes_along_x)); L_mas=length(y_values); u_along_x=u(nodes_along_x); u_along_x=u_along_x(ind); [fl, mes]=fopen('mfile_x.doc', 'w'); fl=fopen('mfile_x.doc', 'w'); %for i=1:L_mas % ya(i)=ua(y_values(i),0.0,5); % R=ya(i)-u_along_x(i); % %fprintf(1,'%10.5f %10.5f\n',y_values(i),u_along_x(i)); % fprintf(fl,'x(%d)=%7.4f y=%10.4f ua=%10.4f R=%10.4f\n',... % i,y_values(i),u_along_x(i),ya(i),R); %end fclose(fl); figure; hold on plot(y_values,u_along_x,'-b'); %plot(y_values,ya,'-m'); legend('u=u(x,0.0)','Location','Best'); %,'ua(x,0.0,t)=x^2+y^2+t^2' title('u=u(x,0.0)'); xlabel('x'); ylabel('u'); grid; end function plot_along_y(p,u,x_val) nodes_along_y=abs(p(1,:)-x_val) < 0.05; [x_values,ind]=sort(p(2,nodes_along_y)); L_mas=length(x_values); u_along_y=u(nodes_along_y); u_along_y=u_along_y(ind); [fl, mes]=fopen('mfile_y.doc', 'w'); fl=fopen('mfile.doc', 'w'); %for i=1:L_mas % ya(i)=ua(0.0,x_values(i),5); % R=ya(i)-u_along_y(i); %fprintf(1,'%10.5f %10.5f\n',u_along_y(i),x_values(i)); % fprintf(fl,'%10.5f %10.5f\n',u_along_y(i),x_values(i)); % fprintf(fl,'y(%d)=%7.4f y_ch=%10.4f ua=%10.4f R=%10.4f\n',... % i,x_values(i),u_along_y(i),ya(i),R); %end fclose(fl); figure; hold on plot(x_values, u_along_y,'-b'); % plot(x_values,ya,'-m'); %legend('u=u(x,y), x=0.0','Location','NorthEast'); legend('u=u(0.0,y)','Location','Best') %,'ua(0.0,y,t)=x^2+y^2+t^2' title('Graph: u=u(0.0,y)'); ylabel('u'); xlabel('y'); grid; end %function [s]=ua(x,y,t) % s=x.^2+y.^2+t.^2; %end pdemesh(p,e,t); axis equal figure pdeplot(p,e,t,'xydata',u,'colormap','cool','colorbar','on','contour','on') % for j=1:5512 % x=p(1,j); % y=p(2,j); % fprintf(1,'j=%4d, x=%4.2f, y=%4.2f, u=%8.4f\n',j,x,y,u(j)) % end x_val=0.0; plot_along_y(p,u,x_val) y_val=0.0; plot_along_x(p,u,y_val) end |

