Программная оболочка для численного решения краевых задач для систем двух связанных параболических уравнений. Программная оболочка для численного решения краевых задач для си. Дипломная работа Программная оболочка для численного решения краевых задач для систем двух связанных параболических уравнений
 Скачать 0.78 Mb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования«Кемеровский государственный университет» Математический факультетКафедра дифференциальных уравненийДИПЛОМНАЯ РАБОТА «Программная оболочка для численного решения краевых задач для систем двух связанных параболических уравнений» студента пятого курса Емельяненко Николая Валерьевича Специальность 010100 – «математика» Научный руководитель: к.ф-м.-н.; доцент В.Г. Борисов _____________________
Кемерово 2008 Содержание Введение 4 §1. Алгоритм численного решения системы двух связанных параболических уравнений 5 1.1. Постановка задачи и основные понятия 5 1.2. Построение алгоритма численного решения 6 §2. Программа численного решения краевой задачи. 11 §3. Пространственно неоднородное стационарное решение модели взаимодействия зоо и фитопланктона 16 §4. Модель брюсселятора 22 Список литературы 25 Приложение 26 ВведениеМногие задачи механики сплошной среды сводятся к решению уравнений в частных производных. Самыми распространенными из них являются уравнения колебания струны (гиперболическое), уравнение Пуассона (эллиптическое) и уравнение теплопроводности (параболическое). В нашей дипломной работе мы рассмотрим параболические уравнения, которые и станут объектом нашего исследования. Данный тип уравнений требует индивидуального подхода, что обусловлено отсутствием единой (сходной) схемы отыскания исходной функции. Не каждое решение имеет аналитический вид и в большинстве случаев может быть представлено только в виде бесконечной суммы степенных рядов. Существует множество пакетов позволяющих построить приближенное и графическое решение данного типа уравнений, такие как MathCAD, MatLAB, Maple. Но для построения решения с их помощью требуется глубокое изучение справочной литературы (не всегда на русском языке), на что затрачивается много времени и усилий. Целью нашего дипломного проекта является создание простой в использовании программы, которая строит таблицу решения параболического уравнения, и экспортирует ее в Excel. Также создается файл решения, открываемый с помощью графического редактора Texplot10. Дипломная работа состоит из введения, основного текста и приложения, в котором приведен текст программы с комментариями. §1. Алгоритм численного решения системы двух связанных параболических уравнений1.1. Постановка задачи и основные понятияРассмотрим систему двух связанных параболических уравнений: 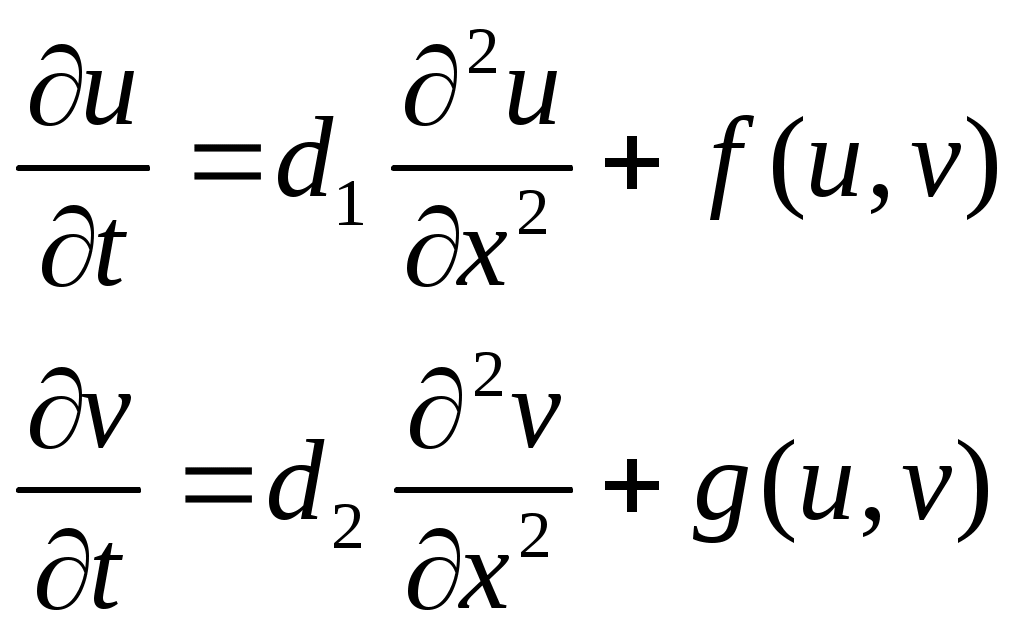 (1.1)в прямоугольнике [0,L]х[0,T] с начальными и граничными условиями    (1.2) (1.3)где  коэффициенты диффузии.Наиболее ценным методом для нахождения приближенного решения данной системы является метод конечных разностей или как его чаще называют метод сеток. Метод конечных разностей состоит в следующем: область непрерывного изменения аргументов заменяется конечным множеством точек (узлов), называемым сеткой; вместо функций непрерывного аргумента рассматриваются функции, определенные в узлах сетки и называемые сеточными функциями. Производные, входящие в уравнения аппроксимируются при помощи соответствующих разностных отношений; каждое уравнение при этом заменяется системой алгебраических уравнений (разностным уравнением). Начальные и краевые условия также заменяются разностными начальными и краевыми условиями для сеточной функции. Область D, на которой определена данная задача, представляет собой прямоугольник (0,L)x(0,T) в системе координат Oxt, а ее граница Г состоит из отрезков прямых x=0, x=L, t=0. Разобьем этот прямоугольник на прямоугольные же части прямыми 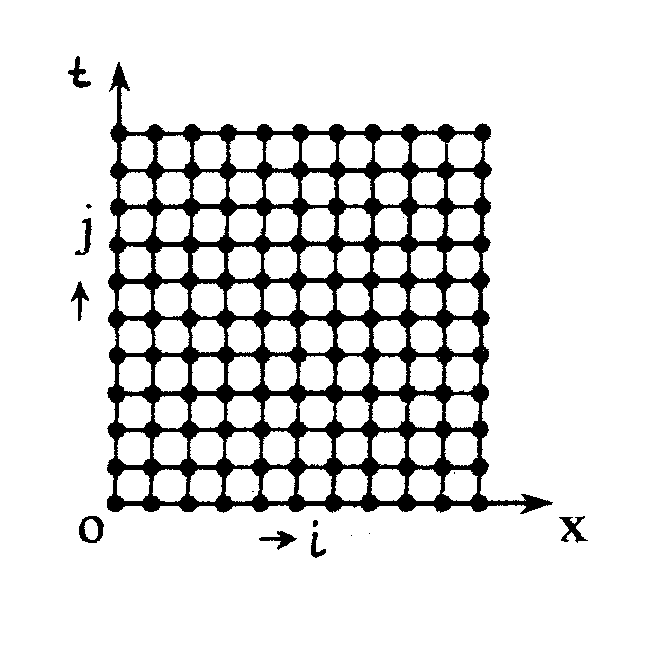 и  , параллельные осям Ot и Ox соответственно, где:   0,1,…,N,  - шаг по пространству,   0,1,…,M,  -шаг по времени.Точки  лежащие на пересечении этих прямых, называются узлами: внутренними, если они принадлежат области D, и граничными, если они лежат на ее границе Г. Совокупность всех узлов в  называют сеткой , а числа h и  называют шагами сетки по переменным x и tсоответственно. Узлы, лежащие на одной прямой при фиксированном j=0,1,…M называют слоем.  Функции, определенные в узлах сетки будем обозначать  и  . Такие функции называются сеточными функциями. Верхний индекс означает номер слоя. |