Программная оболочка для численного решения краевых задач для систем двух связанных параболических уравнений. Программная оболочка для численного решения краевых задач для си. Дипломная работа Программная оболочка для численного решения краевых задач для систем двух связанных параболических уравнений

• Название: Дипломная работа Программная оболочка для численного решения краевых задач для систем двух связанных параболических уравнений
• Анкор: Программная оболочка для численного решения краевых задач для систем двух связанных параболических уравнений
• Дата: 28.07.2022
• Размер: 0.78 Mb.
• Имя файла: Программная оболочка для численного решения краевых задач для си.doc
• Тип: Диплом; #637473
• страница: 4 из 6

§3. Пространственно неоднородное стационарное решение модели взаимодействия зоо и фитопланктона

В качестве примера рассмотрим модель хищник-жертва

, (3.1 )



Сравнивая с (1.1), мы видим, что здесь и , где – численность жертв, – численность хищников, , - изменение числа особей в единицу времени, , - диффузия, , - коэффициенты диффузии.

Система (1), представляет из себя частный случай модели Хищник-Жертва. если f(u) имеет вид, показанный на рис.1.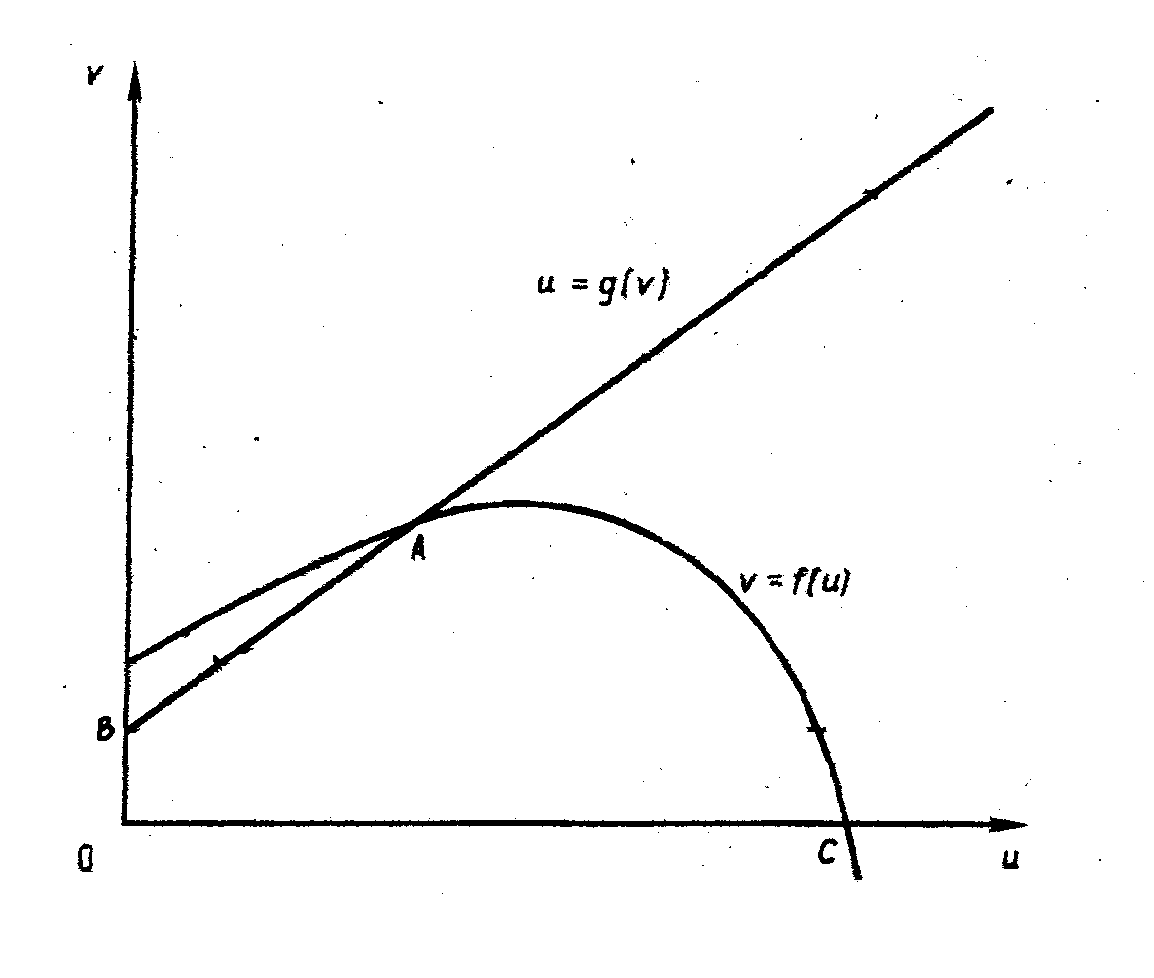



Рис. 1. Качественные особенности членов, описывающих взаимодействие в модели (3.1).
Тот факт, что f(u) имеет определенный максимум при конечном и > 0,

является типичным эффектом перенасе­ления. Мы рассматриваем функцию g(v) вида показанной на рисунке, где точка А пересечения кривых и =g(v) и v = f(u) находится слева от максимума f(u); мы вернемся к этому ниже.

Стационарные решения системы (3.1) - это решения системы ; они обозначены на рис.1 буквами А, В и С. Интерес здесь представляет точка равновесия А, так как она со­ответствует решению ( , ) системы (1.3). Когда , мы тре­буем, чтобы стационарное состояние А было устойчивым, а это, соглас­но условиям (1.16), означает, что f(u) и g(v) в (3.1) удовлетворяют условиям

, (3.2)

где штрихи означают дифференцирование по аргументу.

Собственные значения для анализа устойчивости в линейном при-

ближении (1.7) удовлетворяют уравнению (1.15), которое с уче­том (3.1) принимает вид:

(3.3)

Из первого условия (3.2) ясно, что коэффициент при всегда отрица­телен. Поэтому для того, чтобы могло иметь отрицательную действи­тельную часть, последняя квадратная скобка в (3.3) должна быть для некоторого значения отрицательна.

В силу (3.2) един­ственный член, с помощью которого можно добиться этого, это коэф­фициент при , т.е. и должны быть такими, что Ввиду первого условия (3.2) это последнее неравенство требует неравных коэффициентов диффузии, точнее, . Поскольку

> 0, очевидно, существуют > 0, > 0 и наименьшее положи­тельное N, такие, что член с делает последнюю квадрат­ную скобку в (3.3) отрицательной. Отсюда в свою очередь следует, что одно из решений уравнения (3.3) имеет отрицательную действи­тельную часть, и, следовательно, стационарное состояние неустойчиво в линейном приближении; это и есть диффузионная неустойчи­вость. Как бы ни был мал коэффициент > 0, в спектре Фурье существует только конечный диапазон значений п (так как член доминирует), минимальное из которых N, делающих последнюю квад­ратную скобку в (3.3) отрицательной.

Возможность появления в примере (3.1) диффузионной неустойчи­вости существенно зависит от стационарного состояния , а именно от расположения точки А на рис.1 слева от максимума f(u), так что . Если бы точка А лежала справа от максимума, то f'(u) < 0, последняя квадратная скобка в (3.3) никогда не могла бы быть отри­цательной для любых и и, следовательно, было бы устойчиво.
С помощью построенного алгоритма, приведенного в §1 численно исследовалась одномерная модель взаимодействия зоо - и фитопланктона:



(3.4)

в прямоугольнике [0,L]х[0,T] с начальными и граничными условиями

(3.5 )

(3.6 )

Здесь мы приняли L=2.5. Исследовалась форма пространственно- неоднородного стационарного решения краевой задачи (3.4)-(3.6) при различных коэффициентах диффузии . Построена бифуркационная диаграмма пространственно-однородного стационарного решения по параметрам Приведем результаты этого исследования.

В [4] приведен результат численного исследования системы (3.4)-(3.6) при коэффициентах диффузии 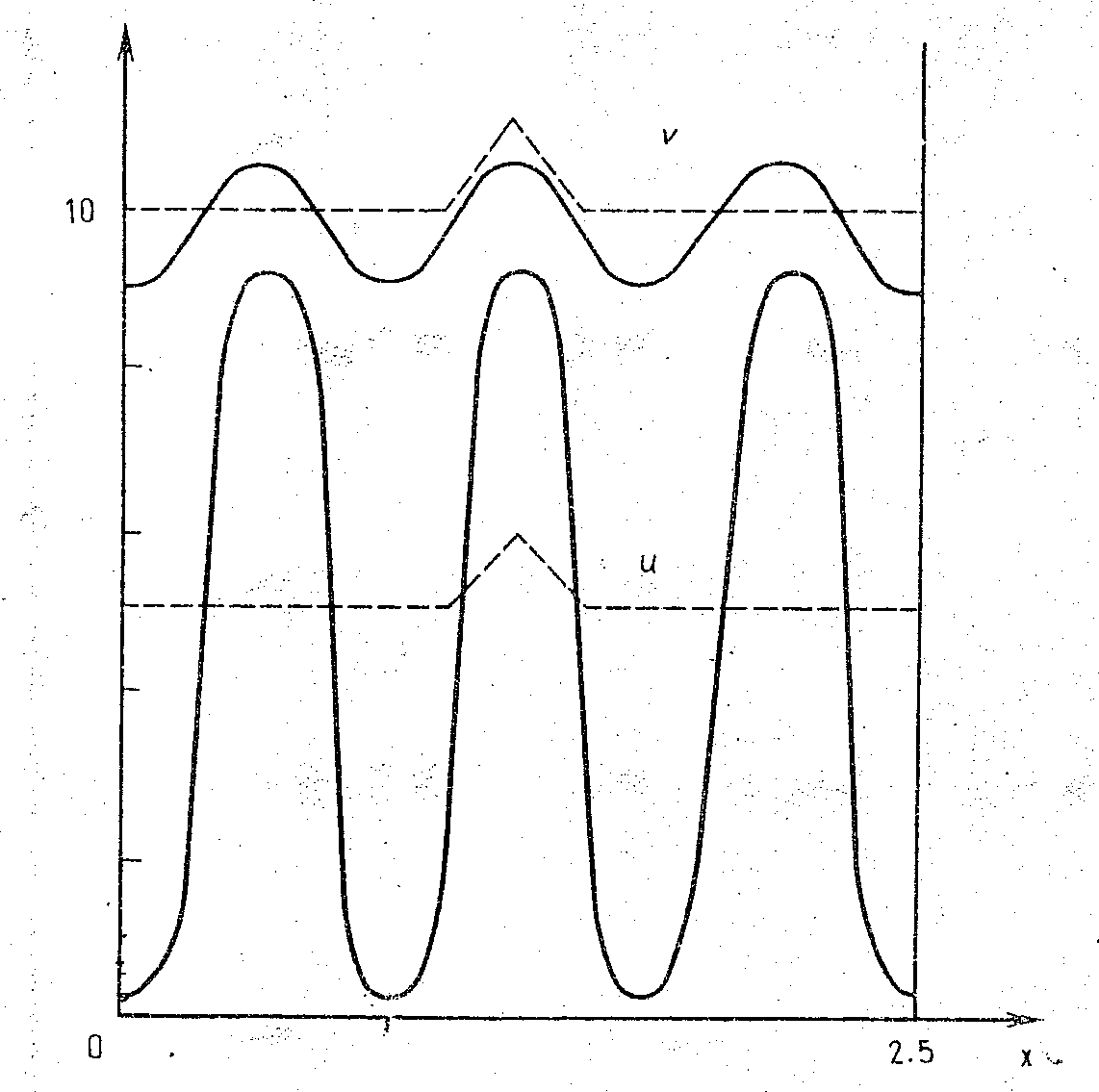. При больших t были найдены устойчивые пространственные структуры конечной амплитуды. Рис.2 иллюстрирует одну из таких структур.



Рис.2. Пространственные структуры (пятнистость) в замкнутой области с нулевым потоком на границе для системы хищник-жертва (5.1)-(5.3) при L=2.5, ; штриховые линии показывают начальные условия.

В первую очередь была исследована система (3.4)-(3.6) при коэффициентах диффузии, приведенных в [4], т.е. с некоторым возмущением в начальный момент времени, как показано на рис.2. Отрезок по времени T=[0,25] , шаг h по пространству равен 0.001.

В результате было получено, что при таких коэффициентах диффузии пространственно-однородное решение неустойчиво и в его окрестности возникает устойчивое пространственно-неоднородное решение. Рис.3 и рис.4 иллюстрирует его постепенное возникновение на разных промежутках времени.

График функции u(x,t)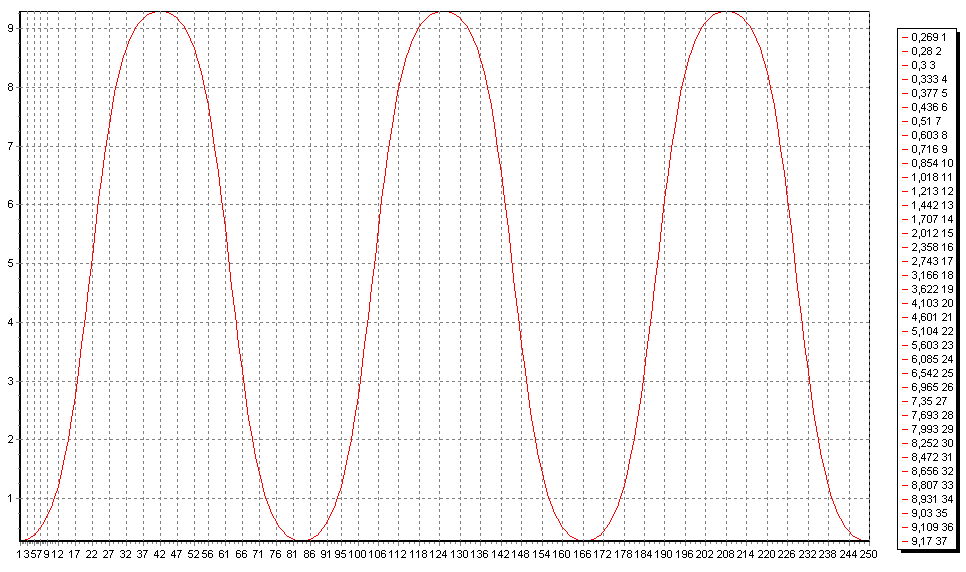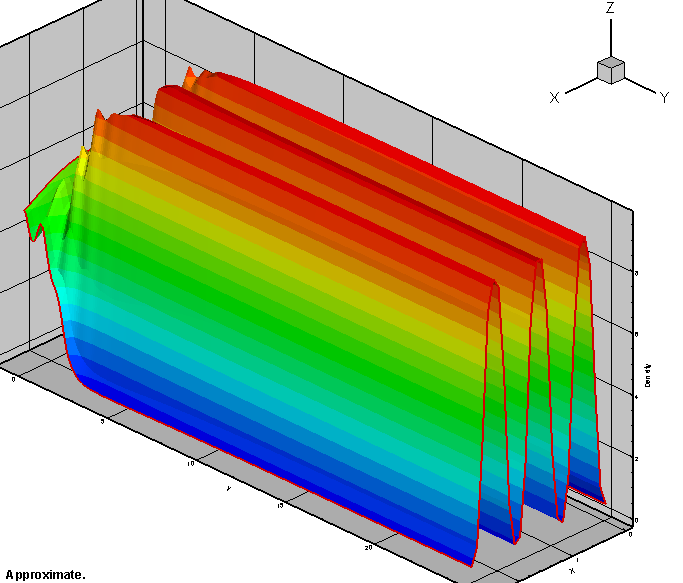

Рис.3 Пространственно-неоднородное решение для фитопланктона

при


График функции v(x,t)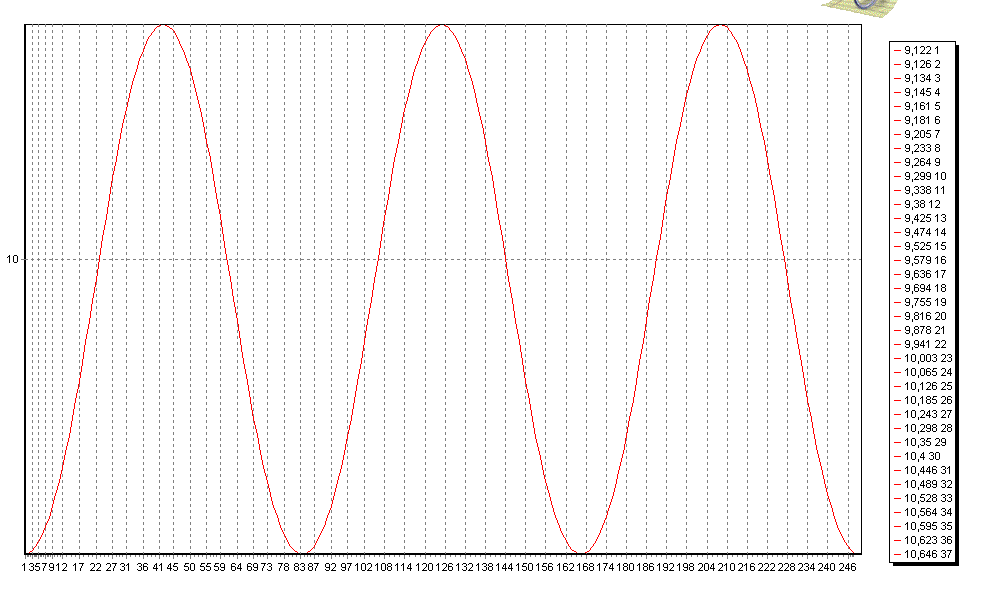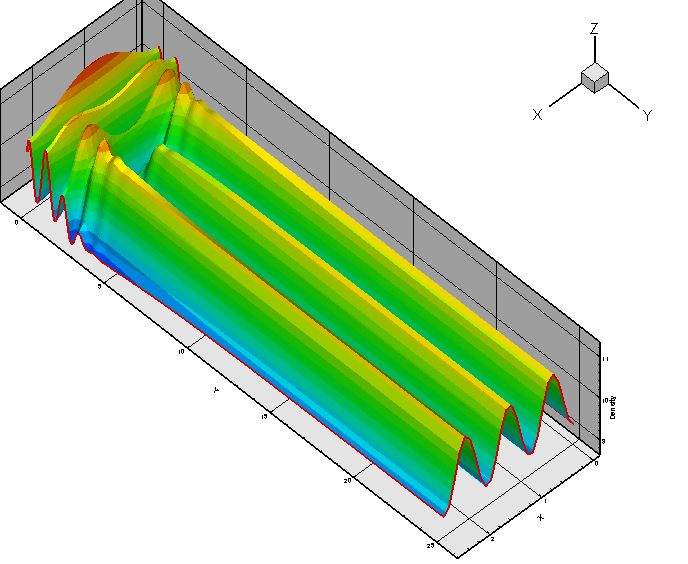



Рис.4. Пространственно-неоднородное решение для зоопланктона

при

Заметим, что полученный результат совпадает с результатом исследования, приведенного в [4]. Детальный характер волн в точности совпадает с рис.2.