Программная оболочка для численного решения краевых задач для систем двух связанных параболических уравнений. Программная оболочка для численного решения краевых задач для си. Дипломная работа Программная оболочка для численного решения краевых задач для систем двух связанных параболических уравнений
 Скачать 0.78 Mb. Скачать 0.78 Mb.
|
§4. Модель брюсселятораМодель брюсселятора является одной из самых известных математических моделей. (Название связано с тем, что она была предложена в брюссельской научной школе.) Эта модель описывает распределение по пространству и изменение со временем реагентов сравнительно узкого класса химических реакций, однако при ее исследовании были выяснены свойства решений многих нелинейных системах: Где u и v концентрации некоторых химических веществ, Вещества u и v остаются в реакторе, поэтому потребуем выполнения следующих краевых условий: Посмотрим, есть ли у уравнения (4.2) какие-нибудь простые решения, например не меняющиеся со временем (их называют стационарными) и однородные по пространству. При этом все производные в (4.2) становятся нулевыми и мы имеем систему обычных алгебраических уравнений: А – (B + 1)u + u2v = 0, Bu – u2v = 0 Ее единственное решение – это u = А, v = B/А. В наших рассуждениях оно будет играть особую роль. Будем менять концентрацию вещества B и начальные распределения концентраций u(х, 0), v(x, 0) и смотреть, как меняется поведение решения. Если концентрация вещества B невелика, то независимо от начальных данных через определенное время установятся концентрации u(x, t) = A, v(x, t) = B/A. Оказывается, такое замечательное решение (устойчивое стационарное, на которое независимо от начальных данных выходят изучаемые распределения параметров при небольших внешних воздействиях) есть у многих нелинейных систем. Оно получило название термодинамической ветви (в случае брюсселятора это решение u = А, v = B/A). На первый взгляд кажется, что такая картина будет иметь место при любых В. Однако это не так. Если зафиксировать начальные концентрации u(х, 0), v(х, 0) и увеличивать значение B, то мы увидим, что начиная с некоторого критического значения B происходит выход на немонотонные стационарные распределения концентраций, например такие, как показаны на рис. 5 и 6. 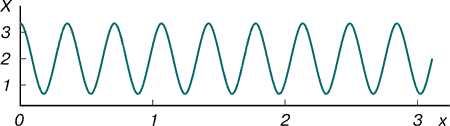 Рис. 5. Стационарные диссипативные структуры, возникающие в модели брюсселятора. Параметры нелинейной среды: А = 2; B = 4,6; d1 = 1,6·10–3; d2 = 8,0·10–3 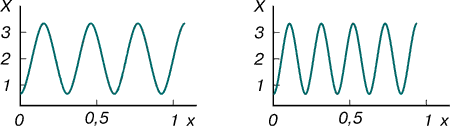 Рис. 6. Распределение концентрации u. Два различных типа структур, возможных в одной и той же нелинейной среде при задании различных начальных данных. Параметры нелинейной среды: A = 2; B = 4,6; d1 = 1,6·10–3; d2 = 8,0·10–3. Исследовали модель брюсселятора при коэффициентах диффузии, приведенных в книге[2], т.е. d1 = 1,6·10–3; d2 = 8,0·10–3 с параметрами нелинейной среды: A = 2; B = 4,6;. Отрезок по времени T=[0,25], по x L=[0,1]. Начальные условия u0=0 v0= x3 В результате было получено. 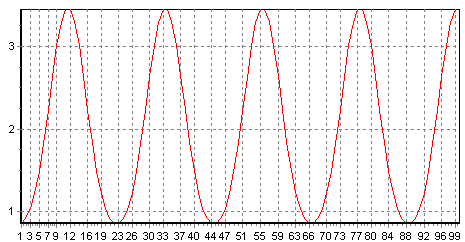 При задании других начальных условий u0=sin(x), v0= cos(x). 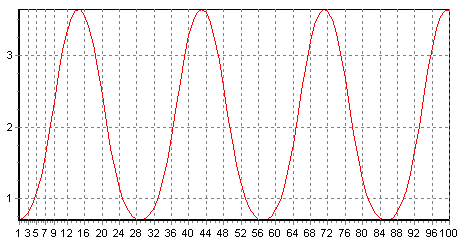 Список литературыВержбицкий, В. М. Основы численных методов [Текст] / В. М. Вержбицкий. – М.: Высш. шк., 2002. – 840с. Компьютеры, модели, вычислительный эксперимент. Введение в информатику с позиций математического моделирования [Текст] / Авт. пред. А.А. Самарский. – М: Наука, 1988. - С.102-106 Романовский, Ю. М., Степанова Н. С., Чернавский Д. С. Математическое моделирование в биофизике [Текст] / Ю. М. Романовский, Н. С. Степанова, Д. С. Чернавский. - М.: Наука, 1975. – 265с. Марри, Дж. Нелинейные дифференциальные уравнения в биологии. Лекции о моделях [Текст] / Дж. Марри .- М.: Мир, 1983.- 397с. Фаронов В. Delphi 6: учебный курс. – СПб.: Питер, 2002. Кэнту М. Delphi 5 для профессионалов. – СПб.: Питер, 2002. |
