2.теория ЭПЮР 2 заочников. Решение задач основано на собирательном

• Название: Решение задач основано на собирательном
• Дата: 29.12.2021
• Размер: 1.26 Mb.
• Имя файла: 2.теория ЭПЮР 2 заочников.docx
• Тип: Решение; #321724

Пересечение поверхности плоскостями частного положения

Плоское сечение геометрического тела представляет собой плоскую фигуру, ограниченную замкнутой линией, все точки которой принадлежат как секущей плоскости, так и поверхности тела.

При сечении поверхности плоскостью частного положения решение задач основано на «собирательном» свойстве вырожденной проекции плоскости, когда проекция искомого элемента фактически уже задана на одной плоскости проекций и ее необходимо достроить на остальной, основываясь на признаке принадлежности.

При пересечении многогранника (призмы, пирамиды и т. п.) в сечении получается многоугольник с вершинами, расположенными на ребрах многогранника (Рис.1,2,3).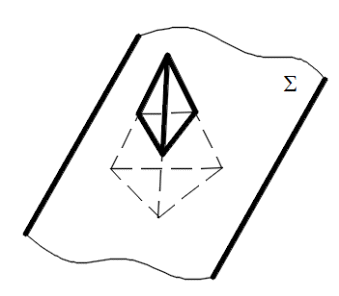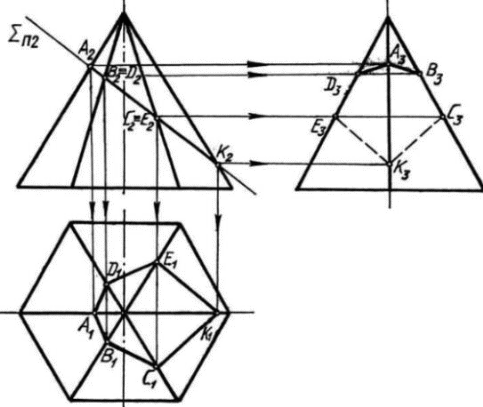



Рис.1

Рис.2

Рис.3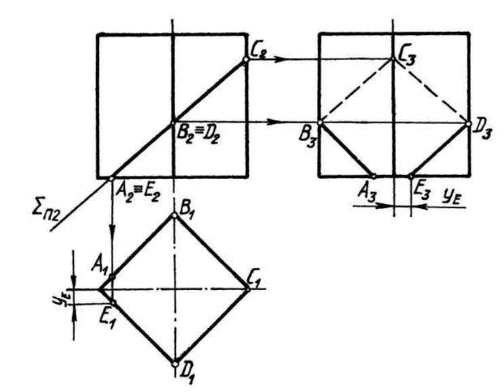




При решении подобных задач необходимо определять видимость отрезков ломаной линии пересечения. На видимых гранях отрезки будут видны, на невидимых – не видны.

В пересечении кривой поверхности с плоскостью получается плоская кривая линия (Рис.4). Точки этой кривой находят при помощи вспомогательных линий – прямых или окружностей, взятых на поверхности тела. Точки пересечения этих линий с секущей плоскостью будут искомыми точками контура криволинейного сечения.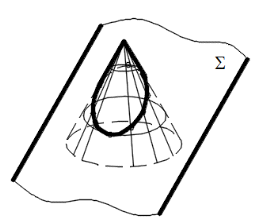


Рис.4

Точки линии пересечения условно разделяют на опорные и промежуточные. Начинаем построение с опорных точек.

К опорным точкам относятся:

– экстремальные точки, то есть наиболее близкие и наиболее удаленные точки от той или иной плоскости проекций: низшая и высшая точки (относительно горизонтальной плоскости проекций), ближняя и дальняя точки (относительно фронтальной плоскости проекций), левая и правая точки (относительно профиль-ной плоскости проекций);

– очерковые точки, то есть точки, проекции которых принадлежат очерку проекции поверхности;

– точки смены видимости, то есть очерковые точки, в которых меняется видимость проекции линии пересечения.

Некоторые опорные токи являются очевидными, то есть точками, которые строятся без дополнительных графических построений. Все остальные точки линии пересечения поверхностей называют промежуточными. При построении линии пересечения в первую очередь определяют опорные точки искомой линии пересечения, а затем – промежуточные.

Особое место занимают задачи по нахождению линии пересечения плоскости с конической поверхностью (рис.5). В зависимости от положения секущей плоскости линией пересечения может быть треугольник, окружность, эллипс, парабола, гипербола.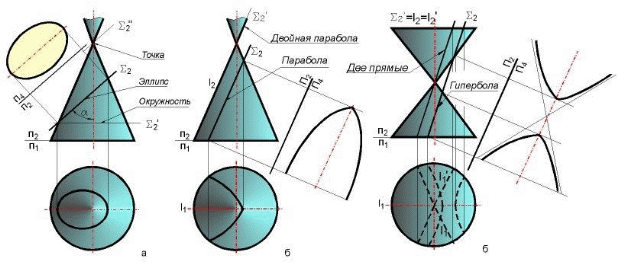



Рис.5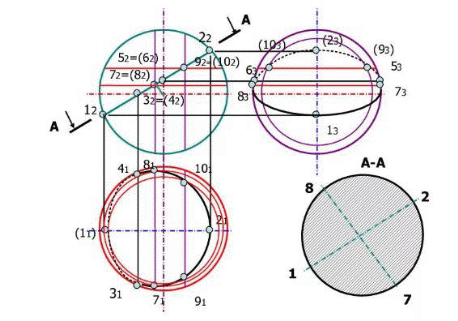


Рис.6

На рис. 6-8 показано построение линии пересечения сферы и конуса с плоскостями частного положения.

На рис. 6 сферу пересекает фронтально-проецирующая плоскость. В сечении получаем окружность, натуральная величина которой определена методом замены плоскостей проекций. Эта окружность фронтальной плоскости проекций вырождается в прямую, совпадающую с секущей плоскостью. На профильной и горизонтальной плоскостях проекций окружность превращается в эллипс, который строится по точкам, по признаку принадлежности (точка принадлежит поверхности, если она принадлежит какай-либо линии, принадлежащей этой поверхности).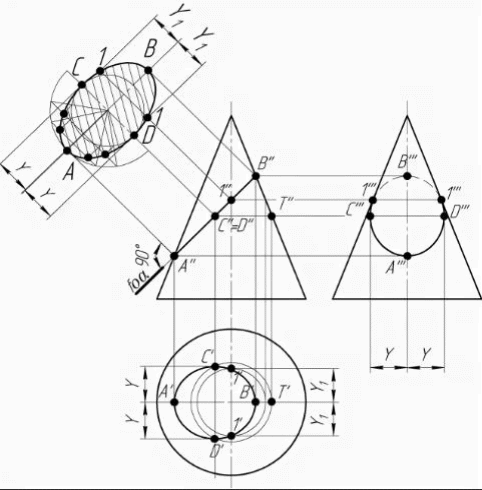

Рис.7
На рис. 7 конус пересекает фронтально-проецирующая плоскость по эллипсу.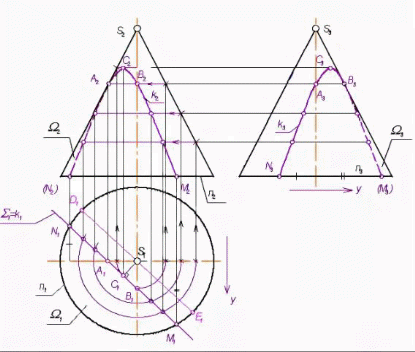



Рис.8

На рис. 8 конус пересекает горизонтально-проецирующая плоскость по гиперболе.

Во всех задачах определяется видимость участков кривой. Точки – границы видимости:

– в задаче на рис. 6 лежат на экваторе и на очерке сферы;

– в задаче на рис. 7 лежат на очерковых образующих конуса;

– в задаче на рис. 8 лежат в плоскости главного меридиана, на очерковых образующих конуса.

Задание 2 (эпюр № 2)

Содержание задания: 2-й эпюр выполняется на формате А3. Построить три проекции линии пересечения сложной поверхности с фронтально-проецирующей плоскостью W. Определить видимость линии пересечения. Построить натуральную величину построенного сечения методом замены плоскостей проекций (рис. 9,10).

Задание на эпюр № 2 представлено в разделе заданий.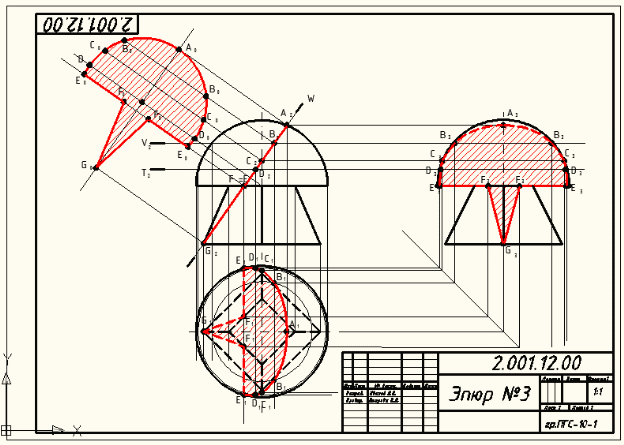



Рис.9



Рис.10


Порядок выполнения

На формате в тонких линиях вычерчивается задание. Данные для вычерчивания комбинированной поверхности взять из задания на эпюр № 2 согласно варианту. Сложная поверхность состоит из двух поверхностей – поверхности вращения (цилиндра, конуса, сферы) и многогранной поверхности (пирамиды, призмы). По двум заданным проекциям (горизонтальной и фронтальной) построить третью проекцию – профильную.

Задачу решаем в два этапа: 1 этап – построить проекции сечения. Так как секущая плоскость – плоскость частного положения, одна проекция сечения совпадает с проекцией этой плоскости, другие проекции строят по точкам пересечения линий каркаса заданных поверхностей с плоскостью.

Линиями каркаса многогранной поверхности являются боковые ребра и ребра основания. Точки пересечения ребер с заданной секущей плоскостью определяются сначала на фронтальной проекции, а затем по линиям проекционной связи – на горизонтальной и профильной проекциях. Линия пересечения – треугольник EFG.

На поверхности полусферы сначала строят точки очевидные – точки пересечения очерков поверхности с плоскостью W. Затем строят точки вспомогательные при помощи вспомогательных секущих плоскостей. На горизонтальной и профильной проекциях полученные точки соединяют в определенном порядке. Получаются кривые линии – участки эллипсов. Затем определяют видимость линии сечения. 2 этап – определить натуральную величину сечения методом замены плоскостей проекций.