Документ Microsoft Word (2). Решение задач по алгебрелогике пк. Роль и место алгебры логики в цифровой вычислительной технике
 Скачать 45.87 Kb.
|
|
Практическое занятие №8 Тема: « Решение задач по алгебре-логике ПК. Роль и место алгебры логики в цифровой вычислительной технике » Цель: изучить основы минимизации ФАЛ с помощью основных законов и аксиом алгебры логики. Получить навыки построения цифровых схем на основе имеющейся ФАЛ. Закрепить знания теоретической области алгебры логики. Краткие сведения из теории Понятие функции алгебры логики Большая часть методов анализа и синтеза всех классов дискретных устройств основана на применении положений алгебры логики (АЛ). АЛ является разделом математической логики. В АЛ все операции проводятся с переменными, принимающими лишь два значения – «истина» и «ложь». Для теории дискретных устройств значение «истина» соответствует логической единице «1», а значение «ложь» – логическому нулю «0». Поэтому АЛ называют еще двухзначной или булевой, по фамилии ее основоположника ирландского математика Дж. Буля (1815–1864). Возможность применения АЛ для синтеза и анализа реальных цифровых устройств (ЦУ) обусловлена использованием в них двоичных сигналов и двустабильных элементов, имеющих два четко выраженных состояния. Например, состояние реле соответствует «1», если оно находится под током, а если реле обесточено – его состояние соответствует «0». В теории часто оперируют таким понятием, как функция алгебры логики (ФАЛ). Функция называется ФАЛ в том случае, если она и ее переменные могут принимать лишь два взаимоисключающих значения «0» и «1». Переменные ФАЛ (ее аргументы) сопоставляют со значениями сигналов на входах ЦУ, а значения ФАЛ (ее результат) – со значениями сигналов на выходах ЦУ. Поскольку реальные ЦУ имеют конечное число входов, то мы будем рас-сматривать функции конечного числа аргументов. Для n двоичных перемен-ых x1, x2, …, xn существует k = 2n наборов значений переменных и R = 2k различных ФАЛ. Например, для одного аргумента x1 существует k = 21 = 2 набора переменных {x1 = 0, x1 = 1} и R = 22 = 4 функции алгебры логики f0 = 0 (константа нуль), f1 = 1 (константа единица), f2 = x1 (повторение x1) и (инверсия x1, т.е. замена всех его значений на обратные). Так как число аргументов и число значений каждого аргумента конечны, конечна и область определения любой ФАЛ. Одним из способов задания ФАЛ является числовой способ. В данном случае каждому набору переменных ставится в соответствие определенное число в двоичной системе исчисления и присваивается ему соответствующий десятичный номер. Функция задается в виде десятичных номеров, на которых она принимает единичные (первый вариант числового задания) или нулевые (второй вариант числового задания) значения. При числовом способе задания ФАЛ каждому набору переменных ставится в соответствие определенное число в двоичной системе исчисления и присваивается ему соответствующий десятичный номер. Функция задается в виде десятичных номеров, на которых она принимает единичные (первый вариант числового задания) или нулевые (второй вариант числового задания) значения. Так, например, для таблицы 1.1.1 по первому варианту ФАЛ будет записана следующим образом: f = {1, 2}x1x2, а по второму варианту – f = {0, 3}x1x2. Для таблицы 1.1.2 числовая запись ФАЛ по первому варианту имеет вид f = {1, 2, 3, 6}x1x2x3, по второму варианту – f = {0, 4, 5, 7}x1x2x3, а для таблицы 2.3 (первый вариант) f = {1, 2, 3, 5, 6, 8, 9, 12, 13, 15}x1x2x3x4 и f = {0, 4, 7, 10, 11, 14}x1x2x3x4 (второй вариант). Знак «» во втором варианте записи указывает на то, что используются наборы нулевых значений функции. В 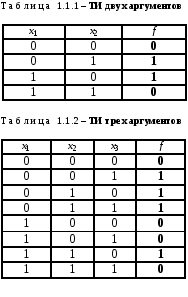 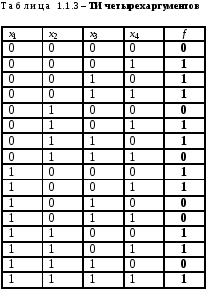 приведенных выражениях в фигурных скобках через запятую записаны в порядке возрастания номера наборов, на которых ФАЛ равна «1» (счет ведется с нуля). Сразу же за фигурными скобками проставляются в виде индексов аргументы ФАЛ, начиная со старшего разряда.Данный способ задания ФАЛ является одним из наиболее простых, однако, его недостаток – слабая наглядность. Минимизация функций алгебры логики При разработке ЦУ обычно возникает задача оптимизации их структуры, т.е. получения экономичной и надежной технической реализации. Это означает, что из двух схем ЦУ, выполняющих одинаковые функции, следует выбирать ту, которая содержит меньшее число элементов, а при одинаковом числе элементов – ту, суммарное число входов используемых элементов которой будет наименьшим. Решение этой задачи связано с проблемой минимизации (упрощения, сокращения) ФАЛ, реализующих данное ЦУ. Минимизация – это процесс нахождения такого эквивалентного выражения ФАЛ, которое содержит минимальное число вхождений переменных. При минимизации могут быть различные варианты: получение выражений с минимальным числом инверсных переменных либо с минимальным числом вхождений какой-либо одной переменной и т.д. Для минимизации функций и поиска наиболее экономичной схемы, реализующей заданное выражение, до сих пор не найдено эффективных алгоритмов, позволяющих решать эти задачи целенаправленно и быстро. Гарантированно найти минимальное выражение для произвольной функции можно лишь методом полного перебора вариантов различных способов группировки в процессе минимизации, а это реально осуществимо лишь при небольшом числе аргументов. С ростом их числа сложность минимизации и поиска экономичной схемы растет экспоненциально и очень скоро становится не под силу ни человеку, ни ЭВМ. С точки зрения подходов к упрощению логических выражений функции, с которыми имеет дело схемотехник, удобно разделить на три группы: функции малого числа аргументов; «объективные» функции многих аргументов и «субъективные» функции многих аргументов. К первой группе можно отнести функции двух–пяти аргументов. Статистический анализ реальных схем цифровой аппаратуры показывает, что разработчики в подавляющем большинстве случаев сталкиваются именно с необходимостью реализовывать именно такие функции. Благодаря малому числу переменных таблицы таких функций короткие, вариантов группировки при минимизации не слишком много, хорошо работает наиболее наглядное геометрическое представление, и в общем, минимизация таких функций любым способом серьезных проблем не вызывает. Ко второй группе – громоздких «объективных» функций – относятся функции более пяти переменных, которые были получены не человеком, а отражают некую объективную природную зависимость. Для этих функций характерно следующее. Во-первых, в них не заложено какой-либо простой логической закономерности, которую можно угадать и использовать для минимизации, т.е. таблица такой функции это просто некая случайная последовательность единиц и нулей. Во-вторых, в силу значительного числа переменных полный перебор вариантов при любом способе поиска минимальной или любой другой экономичной формы практически неосуществим. И, в-третьих, что самое важное, из теоремы О.Б. Лупанова об оценке сложности функций следует, что с ростом числа аргументов доля экономичных по оборудованию функций стремится к нулю, т.е. почти все функции оказываются неупрощаемыми. Следовательно, задача поиска минимальных форм «объективных» функций многих аргументов не только сложна и громоздка, но и с большой вероятностью безнадежна. Это учитывают изготовители элементов, выпуская для реализации функций многих переменных специальные микросхемы – программируемые логические матрицы (ПЛМ) и постоянные запоминающие устройства (ПЗУ). При использовании наиболее распространенных простых вариантов ПЛМ реализация функций будет самой экономичной по затратам аппаратуры, если функция приведена не к минимальной, а к кратчайшей форме. Если же при минимизации ДНФ самую короткую форму получить не удалось, то проигрыш оказывается не-большим, поскольку стоимость реализации на ПЛМ каждой элементарной конъюнкции ДНФ невелика – 1/50 стоимости корпуса. Одной из целей освоения промышленностью ПЛМ как раз и была экономия труда разработчи-ков схем. При использовании ПЗУ на них реализуется непосредственно ТИ функции, т.е. ни записи ФАЛ, ни тем более ее минимизации не требуется вообще. К третьей группе – «субъективных» функций многих аргументов относятся функции, составленные человеком. Особенность их связана с понятием декомпозиции. Это значит, что сложная ФАЛ разбивается на более простые составляющие, из минимальных форм которых в конечном итоге строится аппаратная реализация ЦУ. Однако декомпозиция может быть выполнена неудачно, и устройство в результате будет неэффективным. Для того чтобы избежать этого существуют специальные методы декомпозиции, которые позволяют получать приемлемый результат. Рассмотрим методы минимизации в применении к первой группе функций как наиболее часто и повсеместно встречающихся. Если значение ФАЛ однозначно определено на всех возможных наборах значений ее аргументов, то она называется полностью определенной (заданной). Если же на некоторых наборах значение функции является безразличным и однозначно не определено, то такая функция называется не полностью или частично заданной. В соответствии с этим разделим и методы минимизации (упрощения) ФАЛ на две группы: методы минимизации полностью заданных ФАЛ и методы минимизации не полностью заданных ФАЛ. При минимизации ФАЛ с использованием законов булевой алгебры, функция должна быть представлена в аналитическом виде. Для получения минимальной ФАЛ пользуются аксиомами и законами АЛ, которые позволяют упростить исходное выражение. Например, для упрощения первой функции применяются распределительный закон, законы дополнительности и нулевого множества.  .Для упрощения второй функции используют закон двойственности (правило де Моргана), распределительный закон, законы дополнительности и поглощения.   Порядок выполнения работы 1. Ознакомиться по данным методическим указаниям с правилами работы и основными принципами минимизации ФАЛ. 2. Выполнить минимизацию функций указанных в таблице 2.1 согласно варианту индивидуального задания. 3. Выполнить схематичное построение схемы ЦУ на основе полученных функций. 4. Сделать выводы по работе. Таблица 2.1 – Индивидуальное задание
ВЫВОД: В ходе выполнения ПЗ№8 я изучил основы минимизации ФАЛ с помощью основных законов и аксиом алгебры логики. Получил навыки построения цифровых схем на основе имеющейся ФАЛ. Закрепил знания теоретической области алгебры логики. |