Практическое занятие 1-2. Решение задач принятия решений методом линейного программирования
 Скачать 209.73 Kb. Скачать 209.73 Kb.
|
|
Задание представляется в форме электронного отчета формата MSWordсо следующим содержанием: Титульный лист с данными студента Описания задания. Пошаговое описание выполнения работы со скриншотами и личными поясняющими комментариями Код программы с поясняющими комментариями Вывод Список использованных материалов с указанием URL–адресов Практическое занятие № 1-2 Решение задач принятия решений методом линейного программирования Цель работы: изучить решение задач принятия решений методом линейного программирования Содержание: 1.1. Постановка задачи Задача линейного программирования – задача, в которой требуется минимизировать (максимизировать) линейную форму (целевую функцию) вида  при условиях (ограничениях) 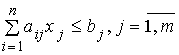 или или 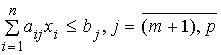 , , Эту же задачу можно записать в матричной форме  (1) (1)Система ограничений на задачу выглядит следующим образом:  (2) (2) Набор чисел удовлетворяющий ограничениям задачи линейного программирования, называется ее планом. Решением задачи линейного программирования будет ее план, минимизирующий (или максимизирующий) линейную форму. 2. Варианты заданий Для различных вариантов построить математическую модель процес- са, обеспечивающую максимум выручки: производственная фирма может выпускать любые из шести видов продукции. Технологии их выпуска, расход ресурсов на единицу продукта, цены гарантированной реализации продукции, а также объёмы сырья и трудовых ресурсов в предстоящем временном периоде представлены в каждом из нижеприведённых вариантов. Вариант № 1
Вариант № 2
Вариант № 3
Вариант № 4
Вариант № 5
Вариант № 6
Вариант № 7
Вариант № 8
Вариант № 9
Вариант № 10
Вариант № 11
Вариант № 12
Вариант № 13
Вариант № 14
Вариант № 15
Дополнительный материал к практическому занятию №1 Цель: научиться решать задачи принятия решений методом линейного программирования Содержание: Постановка задачи В задаче линейного программирования требуется минимизировать (максимизировать) линейную форму (целевую функцию) вида  при условиях (ограничениях) 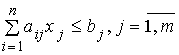 или или 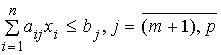 , , Эту же задачу можно записать в матричной форме  (1) (1)Система ограничений на задачу выглядит следующим образом:  (2) (2) Набор чисел удовлетворяющий ограничениям задачи линейного программирования, называется ее планом. Решением задачи линейного программирования будет ее план, минимизирующий (или максимизирующий) линейную форму. Вариант задания
Математическая постановка задачи Целевая функция:  67,2*х1+56,3*х2+52,1*х3+51,2*х4+40,3*х5=41,6*х6 max 67,2*х1+56,3*х2+52,1*х3+51,2*х4+40,3*х5=41,6*х6 maxНабор ограничений:  6х1+7х2+9х3+10х4+11х5+14х6<=504, 15x1+13x2+11x3+9x4+7x5+6x6<=684. Для решения задач линейного программирования в Microsoft Excel подключите к Excel надстройку «Поиск решения» командой Сервис|Надстройки: выберите Поиск решения и щелкните на кнопке ОК.  Для решения задачи нужно подготовить исходную таблицу на рабочем листе Microsoft Excel. Она может выглядеть, например, так: 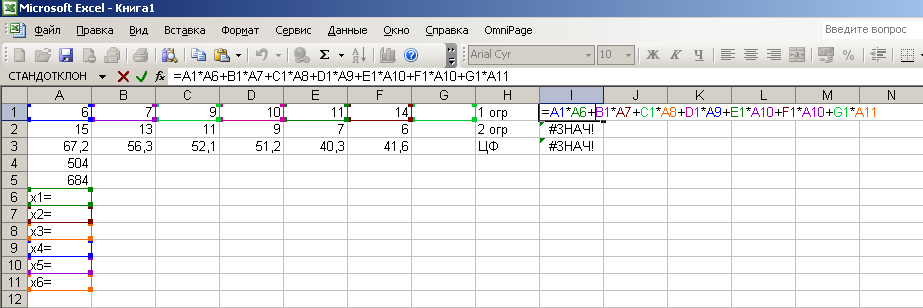 В данном случае ячейки В6…В11 пусты, в них Excel позже разместит оптимальное базовое решение. В ячейки I1 и I2 нужно занести формулы, соответствующие ограничениям линейной модели. Эти формулы будут выглядеть так: =A2*B6+B2*B7+C2*B8+D2*B9+E2*B10+F2*B11 В ячейку I3 нужно занести формулу, соответствующую целевой функции, а именно: Теперь дайте команду Сервис|Поиск решения: 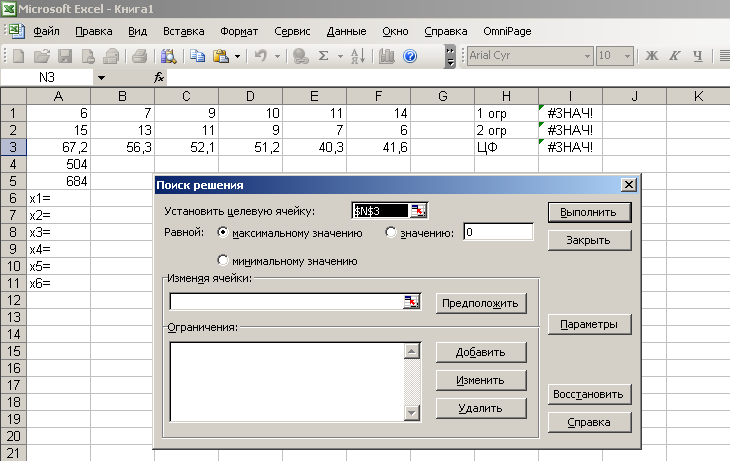 В данном случае целевой ячейкой является I3, она стремится к максимальному решению. Изменяемые ячейки: В6… и В11.  Теперь нужно добавить ограничения. Их будет — собственно ограничения линейной модели (их 2) и ограничения, касающиеся переменных B6:B11 — они должны быть 0 (6 ограничений) и целочисленными (еще 6 условий). Чтобы добавить ограничения, нажмите кнопку Добавить.  Ограничения, касающиеся линейной модели, показаны на следующем рисунке: 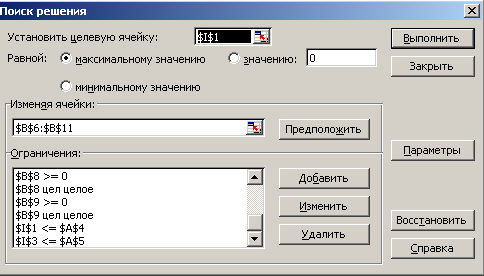 Вот что получится в окне «Поиск решения» после щелчка на кнопке Выполнить: 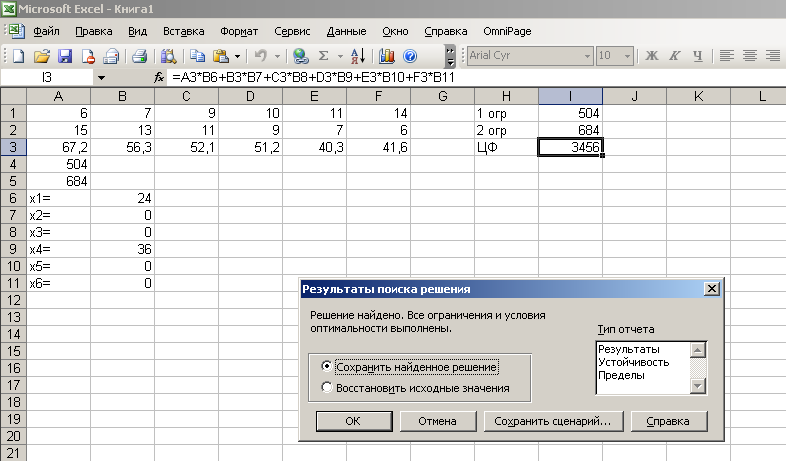 Вывод: максимальную прибыль 3456 тыс. руб. обеспечивает выпуск продукции Х1=24 и х4= 36. Практическая работа. Для решения задачи разработать приложение в среде Delphi 7.0. |
