Решение задач с применением графов при подготовке к огэ по информатике
 Скачать 0.76 Mb. Скачать 0.76 Mb.
|
|
Решение задач с применением графов при подготовке к ОГЭ по информатике Цель: Показать учащимся многообразие задач, решаемых с использованием теории графов. Задачи: Систематизировать и расширить представления учащихся о графах; формировать познавательный интерес к изучению информатики; развивать мыслительные процессы учащихся (анализ, систематизация, классификация) Ходурока: Организационный момент. Приветствие учащихся, проверка готовности к уроку. Домашнее задание – пробный вариант ОГЭ. Тетради с решением собрать в конце урока. С вопросами можно подойти на кружковом занятии (7 урок). Мотивационный момент. Вместо предисловия ЕГЭ по информатике нельзя назвать легким экзаменом. За последние пять лет число школьников, сдающих Единый государственный экзамен по информатике, увеличилось более чем в полтора раза. В нашей школе учащиеся очень часто стали выбирать экзамены по информатике. При подготовке к ОГЭ и ЕГЭ у многих учащихся возникают трудности при решении тех или иных задач, однако, многие типы задания можно решить очень просто с помощью графов. Определения выучить 1. Граф – это наглядное средство представления состава и структуры системы. 2. Граф – это конечное множество точек, некоторые из которых соединены линиями. 3. Точки – называются вершинами, а соединяющие их линии – ребрами. 4. Цепь – это путь по вершинам и ребрам графа, включающий любое ребро не более одного раза. 5. Ориентированный граф – это граф, вершины которого соединены дугами. С помощью таких графов могут быть представлены схемы односторонних отношений. 6. Цикл – это цепь, начальная и конечная вершины которой совпадаю. Граф с циклами называют сетью. 7. - Что такое дерево? Ответ: Дерево – это граф, представленный в виде иерархической системы. 8. Взвешенный граф – это граф, у которого вершины или ребра (дуги) характеризуются некоторой На слайде задание Пример 1. Какая модель позволяет легко и просто решать такие задачи? Граф. В ОГЭ по информатике для 9 класса 3 типа задач можно легко решить, используя теорию графов. Для начала вспомним, что называют графом. Граф – это множество точек, соединенных линиями. Точки – это вершины графа, линии – ребра. Граф называется древовидным, если для каждой пары вершин существует только одно соединяющее ребро. Первый тип задач – задания В3.
Пример 1. Между населѐнными пунктами A, B, C, D, E, F построены дороги, протяжѐнность которых (в километрах) приведена в таблице. Передвигаться можно только по дорогам, указанным в таблице.
Определите длину кратчайшего пути между пунктами A и F. Решение: Точками A, B, C, D, E, F, расположенными по кругу, обозначим населенные пункты. Если в таблице есть число, соединяем точки отрезком и подписываем сверху это число. Отмечаем конечный пункт (в нашем случае это F) и рассматриваем пункты, из которых можно в него попасть. (в нашем случае это A, E, D). В свою очередь в пункт E можно попасть из D, а в пункт D – из C и B. В пункты C и B попадаем из A. Получили начальный пункт. Изобразим дерево всех возможных путей из A в F. Вычислим длины полученных дорог. AF=15, ACDEF=9, ABDEF=10, ACDF=12, ABDF=13. Выбираем длину кратчайшего пути – 9, в предложенных вариантах это ответ №1. Ученик у доски Пример 2. Между населѐнными пунктами A, B, C, D, E построены дороги, протяжѐнность которых (в километрах) приведена в таблице. Передвигаться можно только по дорогам, указанным в таблице.
Определите длину кратчайшего пути между пунктами A и E. Ответ: №2. Среди задач В3 также встречаются такие вариации, которые требуют для решения только внимательности учащегося. Пример 3. В таблице приведена стоимость перевозки пассажиров между соседними населенными пунктами. Укажите граф, соответствующий таблице. 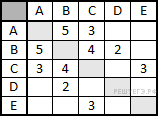 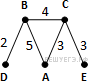 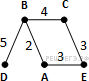 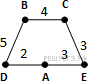 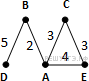 Пример 4. В таблице приведена стоимость перевозки пассажиров между соседними населенными пунктами. Укажите граф, соответствующий таблице.  Второй тип задач – задания В11. 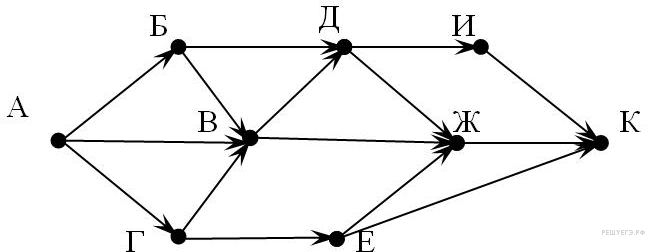 Пример 5. На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? Пример 5. На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?Решение:
Подсчитаем количество путей, последовательно для каждой из вершин графа. Заполним таблицу: 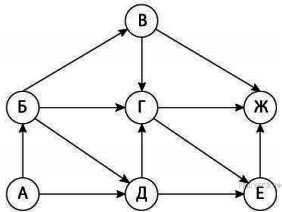 Ответ: 10 различных путей. Ученик у доски Ответ: 10 различных путей. Ученик у доскиПример 6. На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж? Решение: Подсчитаем количество путей, последовательно для каждой из вершин графа. Заполним таблицу:
Ответ: 11 различных путей. Пример 7. У исполнителя Вычислитель две команды, которым присвоены номера: умножь на 4вычти 3 Первая из них увеличивает число на экране в 4 раза, вторая уменьшает его на 3. Составьте алгоритм получения из числа 2 числа 14, содержащий не более 5 команд. В ответе запишите только номера команд. Решение:
Это было решение, основанное на свойствах делимости чисел, и требует логических размышлений. Есть еще способ решения, основанный на применении графов. Возможно, вам будет проще решать задачи, используя его.
Составим дерево возможных решений. Полученное решение 2-8-5-20-17-14, осталось записать его с помощью команд 12122. Ученик у доски. Пример 8. У исполнителя Вычислитель две команды, которым присвоены номера: умножь на 3прибавь 1 Первая из них увеличивает число на экране в 3 раза, вторая увеличивает его на 1. Составьте алгоритм получения из числа 5 числа 60, содержащий не более 5 команд. В ответе запишите только номера команд. Если таких алгоритмов более одного, то запишите любой из них. Подводим итог. Графы значительно упрощают решение некоторых задач. Оставшееся время выполняем самостоятельную работу. Самостоятельная работа. Вариант 1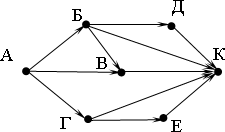 На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? (Ответ: 6) На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? (Ответ: 6)Между населѐнными пунктами A, B, C, D, E, F построены дороги, протяжѐнность которых (в километрах) приведена в таблице. Передвигаться можно только по дорогам, указанным в таблице. Определите длину кратчайшего пути между пунктами A и F. 1) 7 2) 9 3) 11 4) 15
Ответ: 7 У исполнителя Квадратор две команды, которым присвоены номера: возведи в квадратприбавь 3 Первая из них возводит число на экране во вторую степень, вторая увеличивает его на 3. Составьте алгоритм получения из числа 1 числа 25, содержащий не более 5 команд. В ответе запишите только номера команд. Если таких алгоритмов более одного, то запишите любой из них. (Ответ: 21222) Самостоятельная работа. Вариант 2На рисунке –– схема дорог, связывающих города А, Б, В, Г, Д, Е, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? Ответ: 7 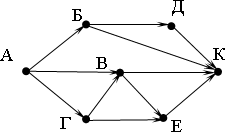 Между населѐнными пунктами A, B, C, D, E, F построены дороги, протяжѐнность которых (в километрах) приведена в таблице. Передвигаться можно только по дорогам, указанным в таблице. Определите длину кратчайшего пути между пунктами A и F. Ответ: 9 1) 7 2) 9 3) 11 4) 15
У исполнителя Вычислитель две команды, которым присвоены номера: умножь на 5прибавь 1 Первая из них возводит число на экране во вторую степень, вторая увеличивает его на 3. Составьте алгоритм получения из числа 1 числа 56, содержащий не более 5 команд. В ответе запишите только номера команд. Если таких алгоритмов более одного, то запишите любой из них. Ответ: 21212 Озвучить оценки, дать домашнее задание (поменяться вариантами). Тема: Графы. Использование графов для решения прикладных задач Цели-результаты: - Предметные: обобщить и систематизировать знания о графах, их видах и свойствах; рассмотреть типы задач, которые можно решить с использованием графов; отработать навыки преобразования ориентированного графа в дерево; сформировать навыки построение путей в графе, поиска кратчайшего пути; закрепить навыки работы в среде текстового процессора Microsoft Word; - Личностные: Развитие логического мышления, т.е. умения анализировать, обобщать, классифицировать, составлять план при выполнении практической работы на компьютере; Развитие познавательных умений: выделять главное, планировать работу, вести поисковую деятельность; Критически оценивать результаты своего труда, регулировать и контролировать свои действия при работе на компьютере; - Метапредметные:развитие у учащихся универсальных учебных действий Регулятивные: умения соотносить свои действия с полученными результатами. Коммуникативные: Умение высказывать свое мнение, правильно его формулировать, аргументировать собственную позицию при выработке общего решения в совместной деятельности; Познавательные: умения создавать графические информационным модели; умения представлять, анализировать и обобщать информацию, полученную в ходе исследования; умения делать выводы, формулировать алгоритм. Тип урока: обобщения и систематизации знаний, проблемноориентированый Виды работ: фронтальная беседа, работа в группах, обсуждение, доклады учащихся Оборудование: на доске эпиграфы, граф дорог; презентация, результаты ПЛАН УРОКА Организационный момент, приветствие - 2 минуты Проверка домашнего задания и демонстрация путей решения задач с использованием графов – 5 минут; Постановка проблемы – 3 минуты; Анализ проблемной ситуации и возможные пути ее решения, определение темы урока – 2 минуты; Актуализация опорных знаний, умений, навыков, которые потребуются для решения поставленных задач на уроке - 4 минуты; Возврат к проблемной ситуации с задачей и обсуждение способов решения – 2 минуты; Решение задачи – 15 минут; Анализ результатов - 3 минуты; Проверка решения с использованием сервиса Google-карты – 5 минут; Подведение итогов урока - 2 минуты; Домашнее задание - 2 минуты; ХОД УРОКА «Безногий, ковыляющий по верной дороге, обгоняет всадника, скачущего не туда» Френсис Бэкон «Мир уступает дорогу тому, кто знает куда идет» Ральф Уолдо Эмересон «Дорога, которая раньше была почти непроходимой, теперь кажется лёгкой: все препятствия, однажды преодолённые, нам уже не страшны» Б. Вербер Приветствие. Здравствуйте, ребята! Сегодняшний наш урок я бы хотела начать со слов Френсиса Бэкона и Ральфа Уолдо Эмерсона «Безногий, ковыляющий по верной дороге, обгоняет всадника, скачущего не туда», «Мир уступает дорогу тому, кто знает куда идет». Конечно, эти философские высказывания связаны с выбором правильного жизненного пути. И вы стоите перед таким выбором в этом учебном году, как выпускной класс. Но сегодня на уроке мы увидим, что данные высказывания можно применить и к обычным путешествиям. Проверка домашнего задания Но прежде чем мы начнем новую тему давайте вспомним, какую тему мы изучали на прошлом уроке? Чтобы было задано домой? Как вы решали данную задачу? Вызывается 1 человек к доске, для демонстрации решения домашней задачи. Задача на Слайде 2  Решение Необходимо построить деревья вариантов, согласно правилам записанным в условии задачи. Ожидаемое решение: 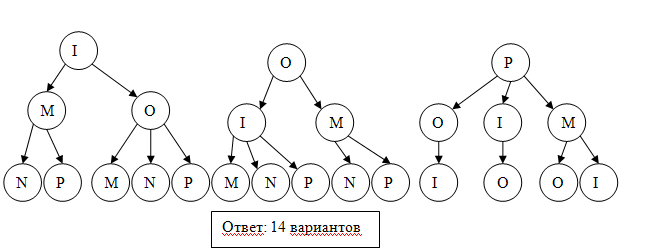 расставляем бусины на первом месте (по правилу возможны три варианта) Расставляем бусины на втором месте, исключая те варианты, когда бусина стоит на первом месте; Расставляем бусины на третьем месте по правилу, исключая варианты, когда такая же бусина стоит на втором месте. Считаем количество веток полученного дерева Учитель: - Каким способом мы решили данную задачу? (Ожидаемый ответ: построили дерево возможных вариантов и посчитали его ветви) Данным методом так же можно решать и много других задач, в чем мы сегодня с вами убедимся. 3. Постановка проблемы. Давайте рассмотрим следующую задачу, с которой каждый из нас может однажды столкнуться в своей жизни: Учеников 9-х классов города Алчевска пригласили в колледж Восточно-украинского национального университета им. Даля на день открытых дверей, который будет проходить в главном корпусе университета. Маршрутные автобусы из города Алчевск приходят на железнодорожный вокзал, от которого отправляются множество автобусов. Сопровождающий получил следующую упрощенную схему следования маршрутных такси до пункта назначения. Слайд 3 (на слайде схема дорог) 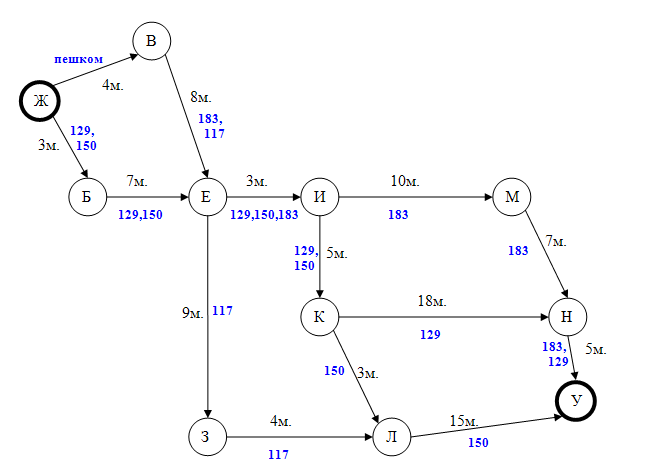 Расшифровка остановок на Слайде 4 (приведен скриншот): 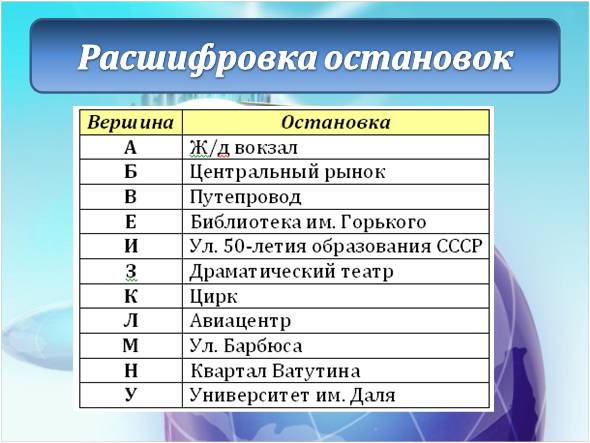 Помогите определить: Самый короткий путь без пересадок, время пути, номер маршрутного автобуса и его маршрут. 4. Анализ проблемной ситуации и возможные пути ее решения На слайде 5 вопросы: - Можем ли мы сразу решить эту задачу, только посмотрев на схему? (ожидаемый ответ: нет) - Что нам мешает решить задачу? (ожидаемый ответ: слишком много возможных вариантов, нужно проследить каждый маршрут, в которых легко запутаться, не все дороги совпадают с маршрутами автобусов, нужно учесть варианты с пересадками) - А что из изученного нами поможет решить эту задачу? (Ожидаемый ответ: графы) Совершенно верно, данная схема представляет собой граф дорог. И тема нашего урока «Решение задач с помощью графов» Давайте с вами вспомним, что же такое граф и какие бывают графы. Актуализация (фронтальный опрос): На слайде 6 вопросы к актуализации. - Что такое граф? - Из каких объектов состоит граф? (Ожидаемый ответ: ребра, вершины) - В чем особенности взвешенного графа? (Ожидаемый ответ: у взвешенного графа ребра характеризуются дополнительной величиной – весом ребра) - Наш граф является взвешенным или нет? (Ожидаемый ответ: взвешенным) - Что является весом ребер в графе? (Ожидаемый ответ: время пути между остановками в минутах) - Чем отличается ориентированный граф, от неориентированного? (Ожидаемый ответ: в ориентированных графах указывается направление пути) - Наш граф является ориентированным или нет? (Ожидаемый ответ: ориентированным) - Что такое дерево? (Ожидаемый ответ: Дерево – это граф, представленный в виде иерархической системы) Возврат к проблемной ситуации и обсуждения способа ее решения Вернемся к нашей задаче и посмотрим на нее внимательно. Как можно решить эту задачу? Ожидаемые ответы: составить дерево возможных вариантов, исключая пересадки, где это необходимо. После ответов демонстрируется слайд 7: 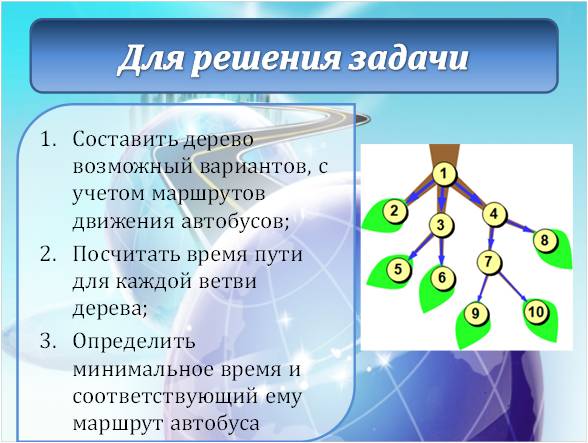 Посчитать суммарное время поездки и определить самый короткий путь, определить номер автобуса и маршрут по расшифровке вершин графа. Для решения этой задачи вы построите дерево возможных вариантов в текстовом процессоре Word. После чего мы обсудим получившиеся результаты При работе на компьютере помните о правилах безопасной работы: расстояние между монитором и глазами должно быть не меньше 30 см, руки и кисти должны лежать на столе, спина прямая. Если почувствуете напряжение в глазах, переведите взгляд на предмет вдали и сделайте зарядку для глаз. Для ускорения работы воспользуйтесь шаблоном Маршрут.doc, который находится в Материалах. Так же в материалах находится файл с задачей Задача_маршрут. Обязательно сохраните файл в свою рабочую папку. А после того, как определите маршрут, расшифруйте по таблицу название вершин графа, чтобы понять через какие остановки следует автобус. Решение задачи за компьютерами. Ответы: Количество возможных путей: 8 Самый короткий маршрут 150 автобус, 35 минут (183 – 37 минут, 117 и 129 – 40 минут) Анализ результатов Зачитывает один из учеников, что у него получилось. (Демонстрируется выполненная работа с использованием сетевой программы). Результат записывается на доске. Учитель: У всех так получилось? Есть те, у кого получились другие варианты? Кто не успел выполнить задание? На слайде 9 демонстрируются правильные результаты: 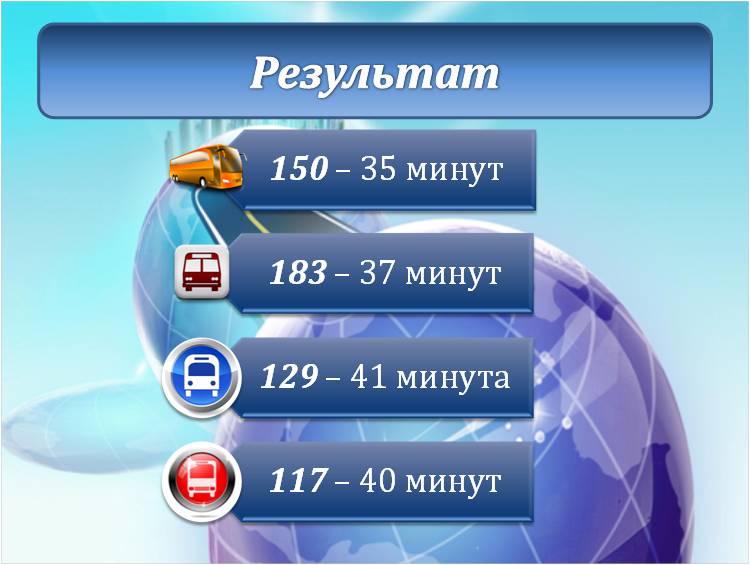 Проверка результата А теперь я предлагаю вам проверить наши расчеты. Один из учеников заранее получил особое домашнее задание. С помощью сервиса Google-карты определить возможные маршруты следования от ж/д вокзала до университета и найти самый короткий путь. Ученик демонстрирует результаты свой работы Демонстрация выполнения задания в Google-картах. (Ответ должен совпадать) Приведены скриншоты выполненного учеником задания 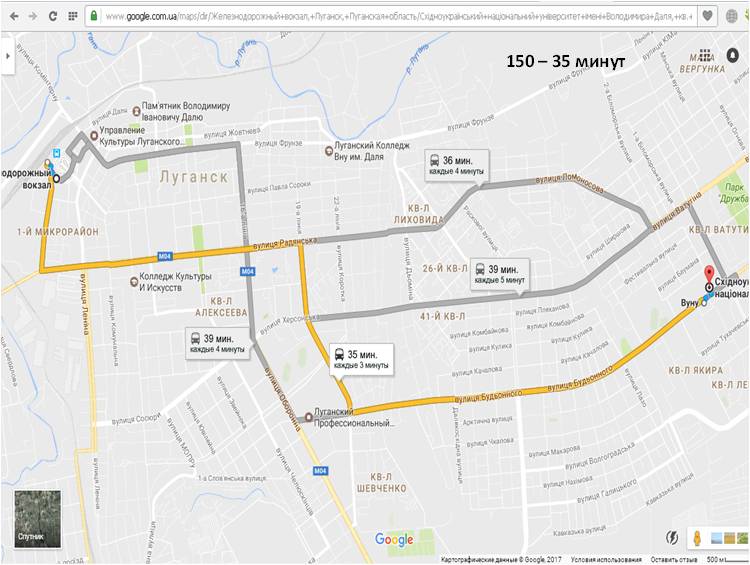 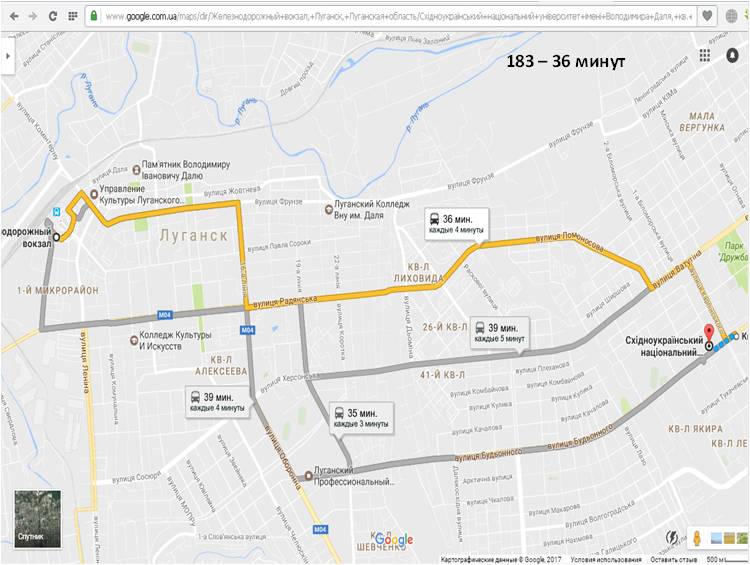 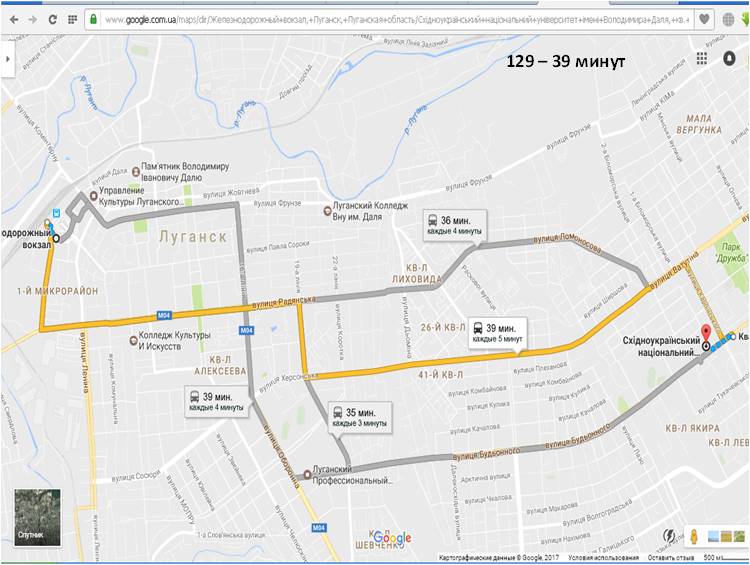 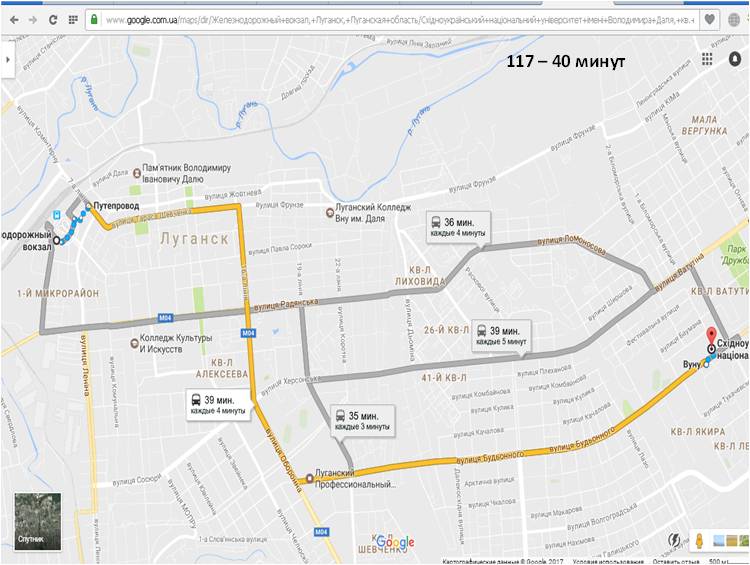 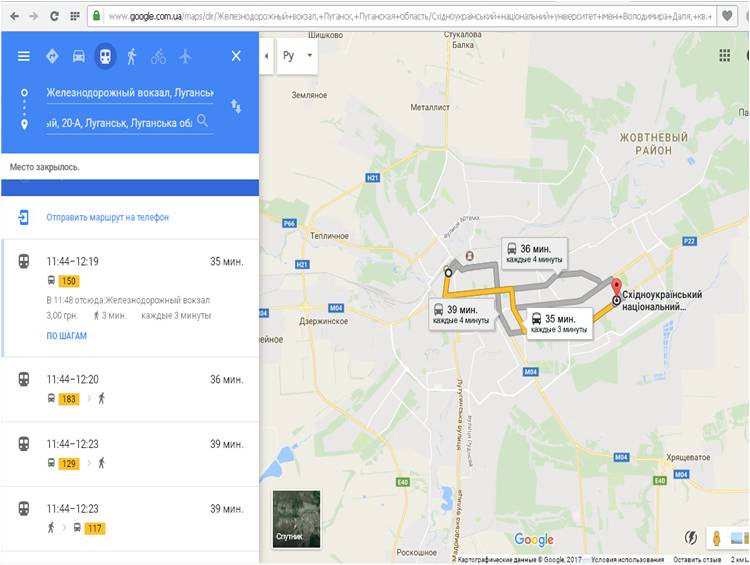 Для сравнения результатов учитель демонстрирует на слайде 10 оптимальный маршрут 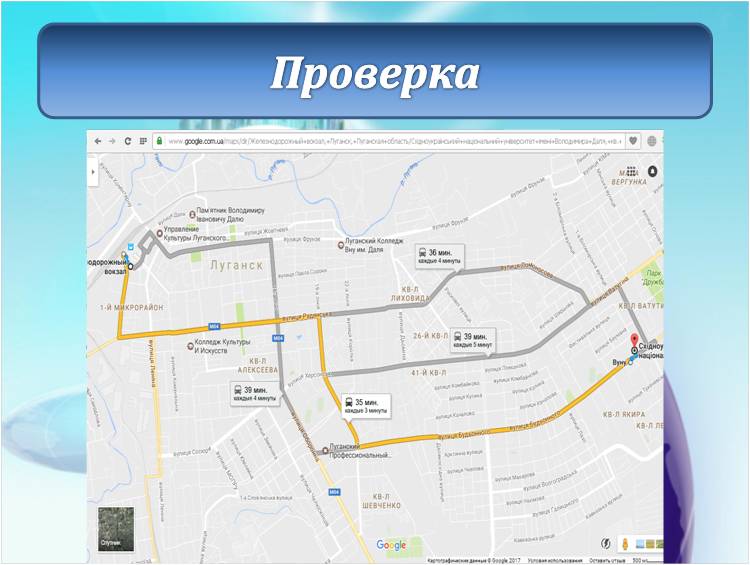 Подведение итогов и оценивание Итак, как вы видите результаты наших расчетов и сервиса Google-карты совпадают. Значит, мы можем сделать вывод о том, что задачу мы решили правильно. Рефлексия - Понравилась вам задача? - Легко ли мы нашли самый короткий путь, после изучения темы графы? - оценивание Закончить наш урок я хочу словами Бернара Вербера «Дорога, которая раньше была почти непроходимой, теперь кажется лёгкой: все препятствия, однажды преодолённые, нам уже не страшны». Я надеюсь, что знания полученные сегодня на уроке помогут вам в ваших путешествиях, а сегодняшний наш маршрут к университету, заставит задуматься, чем бы вы хотели заниматься в жизни и какую профессию выбрать. Нам осталось только записать домашнее задание. Откройте дневники и запишите: Параграф 1.3 Задача №6. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
