Инвестиции. Инвестиции решение задач. Решение задач
 Скачать 272.22 Kb. Скачать 272.22 Kb.
|
|
Решение задач Вариант 1 Задача 1 У компании имеются два проекта - А и Б. Каждый проект имеет издержки в 10 тыс. р., альтернативные издержки для каждого проекта составляют 12 %. Ожидаемые денежные потоки, генерируемые этими проектами представлены в таблице 3.1.4. Денежные потоки по двум проектам, А и Б
Задания: а) подсчитать период окупаемости, чистую приведенную стоимость, коэффициент внутренней нормы доходности для каждого проекта; б) решить, какой проект должен быть принят, если они независимые; в) решить, какой проект должен быть принят, если они взаимоисключаемые; Решение: а) 1. Расчет периода окупаемости. Окупаемость проекта, А (лет):  Итак, ожидаемый поток доходов меняется из года в год, период окупаемости можно определить, суммируя доходы по годам до тех пор, пока их сумма не станет равной первоначальному вложению. Через 2 года накопленный доход 9,5 тыс. р. (6,5 + 3) меньше капвложений, через 3 года - 12,5 тыс. р. (6,5 + 3 + 3) — больше. Точный расчет срока окупаемости: 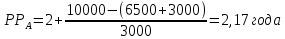 Аналогичный расчет сделаем для проекта Б. Окупаемость проекта Б (лет): 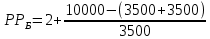 =2,86 года =2,86 годаПри независимости оба проекта следует принять, т. к. срок окупаемости не превышает срока эксплуатации проектов. Если следует выбрать один, то более предпочтительным оказывается проект, А, имеющий меньший срок окупаемости. 2. Чистая приведенная стоимость: 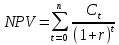 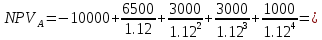 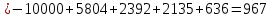 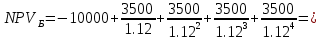 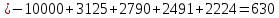 При независимости оба проекта следует принять, т. к. NPV для обоих проектов положителен. Если следует выбрать один, то более предпочтительным оказывается проект, А, имеющий больший чистый дисконтированный доход. 3. Внутренняя норма доходности: Для расчета внутренней нормы доходности воспользуемся приблизительным расчетом на основе формулы: 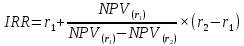 В качестве r1 используем исходную ставку дисконтирования 12 %. В качестве r2 возьмем, например, 20 %. Рассчитаем NPV со ставкой 20 %: 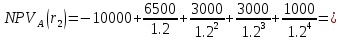 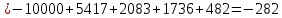 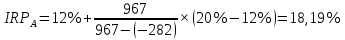 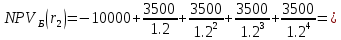 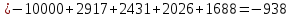 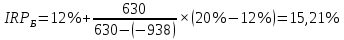 При независимости проекты следует принять, если PI не превышает стоимости привлекаемых средств. Если следует выбрать один, то более предпочтительным оказывается проект, А, имеющий большую внутреннюю норму доходности. б) По всем рассмотренным критериям оба проекта являются приемлемыми. Таким образом, оба проекта должны быть приняты, если они независимые. в) При альтернативности проектов выбрать следует проект А. Он лучше по всем показателям. Задача 2. Размер инвестиции - 200 000 тыс.руб. Доходы от инвестиций в первом году: 50 000 тыс.руб.; во втором году: 50 000 тыс.руб.; в третьем году: 90000 тыс.руб.; в четвертом году: 110000 тыс.руб. Ставка дисконтирования равна 15%. Определить период по истечении которого инвестиции окупаются. Также определить чистый дисконтированный доход (ЧДД), индекс прибыльности. Сделать вывод. Решение: Чистые денежные потоки рассчитываются следующим образом: CFi/(1+r)t, где CFi – денежные потоки по годам. r – ставка дисконта. t – номер года, 1-й, 2-й, 3-й и т.д. Например, в первый год получим чистый денежный поток, равный 50000 х (1+0,15)1=43478,26 (т.р.) Чистый дисконтированный доход ЧДД (английское сокращение NPV) ЧДД = ∑CFi/(1+r)i – I, где I – размер инвестиций. ∑CFi/(1+r)i – сумма чистых денежных потоков. Заполним таблицу с расчетными данными.
ЧДД = 3354,76 тыс. руб. Срок окупаемости простой равен 3+10000/110000=3,09 (лет). Срок дисконтированный равен 3+ 59538,09 /62892,86 =3,95 (лет). Индекс прибыльности рассчитывается следующим образом: PI=∑CFi/(1+r)i /I (чистые денежные потоки делим на размер инвестиций). Индекс прибыльности равен = (43478,26 + 37807,18 + 59176,46 + 62892,86) / 200000=1,02. Вывод: Таким образом, ЧДД>0, Индекс прибыльности (рентабельности инвестиций) >1. Срок окупаемости простой и дисконтированный менее 4 лет. Что говорит о том, что проект окупается в среднесрочной перспективе, и его можно считать эффективным. Задача 3. В рассмотрении находится инвестиционный проект. Согласно ему инвестор должен вложить 10 тыс. у. е. Обещанный ему среднегодовой доход составляет 3 тыс. у. е. Найти срок окупаемости, выраженный в годах и месяцах. Решение: Доход поступает равномерно, поэтому используем следующую формулу: PP = K/Dср = 10000/3 тыс. = 3,33 года. Выразим нецелую часть года в месяцах: 0,33 х 12 = 4 месяца. Ответ: Срок окупаемости инвестиционного проекта — 3 года и 4 месяца. Вариант 2 Задача 1. Инвестиционный проект генерирует неравномерный денежный поток. Найти срок окупаемости проекта. Денежный поток по проекту, у. е.
Решение: Сумма доходов за первые 4 года составляет 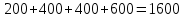 у. е., что покрывает инвестиции с избытком, т. е. срок окупаемости — 4 года. у. е., что покрывает инвестиции с избытком, т. е. срок окупаемости — 4 года.Найдем более точно срок окупаемости: через 3 года непокрытый остаток капиталовложений (Кост) равен: 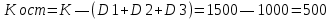 у. е., который может быть покрыт за 0,83 (500/600) четвертого года, т. е. за 10 (0,83 у. е., который может быть покрыт за 0,83 (500/600) четвертого года, т. е. за 10 (0,83 Ответ: Срок окупаемости инвестиций 3 года и 10 месяцев. Задача 2. В инвестиционный проект предлагается вложить 1600 у. е. Обещанный среднегодовой доход составляет 400 у. е. Ожидается, что ставка доходности (дисконтирования) не будет меняться и будет составлять 10 % годовых. Найти абсолютный и дисконтированный срок окупаемости. Решение: Абсолютный срок окупаемости находится непосредственно из формулы, т. к. поток доходов равномерный: 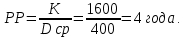 Для расчета дисконтированного срока окупаемости считаем сумму дисконтированных доходов нарастающим итогом до тех пор, пока она не превысит капиталовложения. Сумма доходов за первые 5 лет составляет: 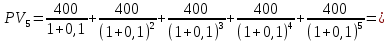 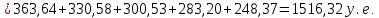 что меньше суммы капиталовложений. что меньше суммы капиталовложений.Сумма доходов за первые 6 лет составляет: 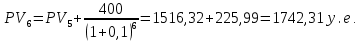 , что покрывает исходную сумму капиталовложений, т. е. срок окупаемости — 6 лет. , что покрывает исходную сумму капиталовложений, т. е. срок окупаемости — 6 лет.Более точно: через 5 лет непокрытый остаток капиталовложений (Кост) равен: 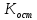 = K – = K – 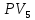 = 1600 — 1516,32 = 83,68 у. е., который может быть покрыт за 0,37 (83,68/225,99) шестого года, т. е. за 4,4 (0,37 = 1600 — 1516,32 = 83,68 у. е., который может быть покрыт за 0,37 (83,68/225,99) шестого года, т. е. за 4,4 (0,37 Ответ: Абсолютный срок окупаемости инвестиций составит 4 года; дисконтированный срок окупаемости — 5 лет и 4,4 месяца. Задача 3. Компания N располагает двумя альтернативными вариантами инвестиционных проектов, требующих одинаковых вложений. Данные, характеризующие эти проекты, приведены в таблице. Найти срок окупаемости инвестиций для каждого из проектов. Выбрать проект для реализации с точки зрения: а) сохранения ликвидности; б) получения дохода; в) эффективности. Принять решение на основе учетных оценок. Денежные потоки по проектам, А и Б, у. е. 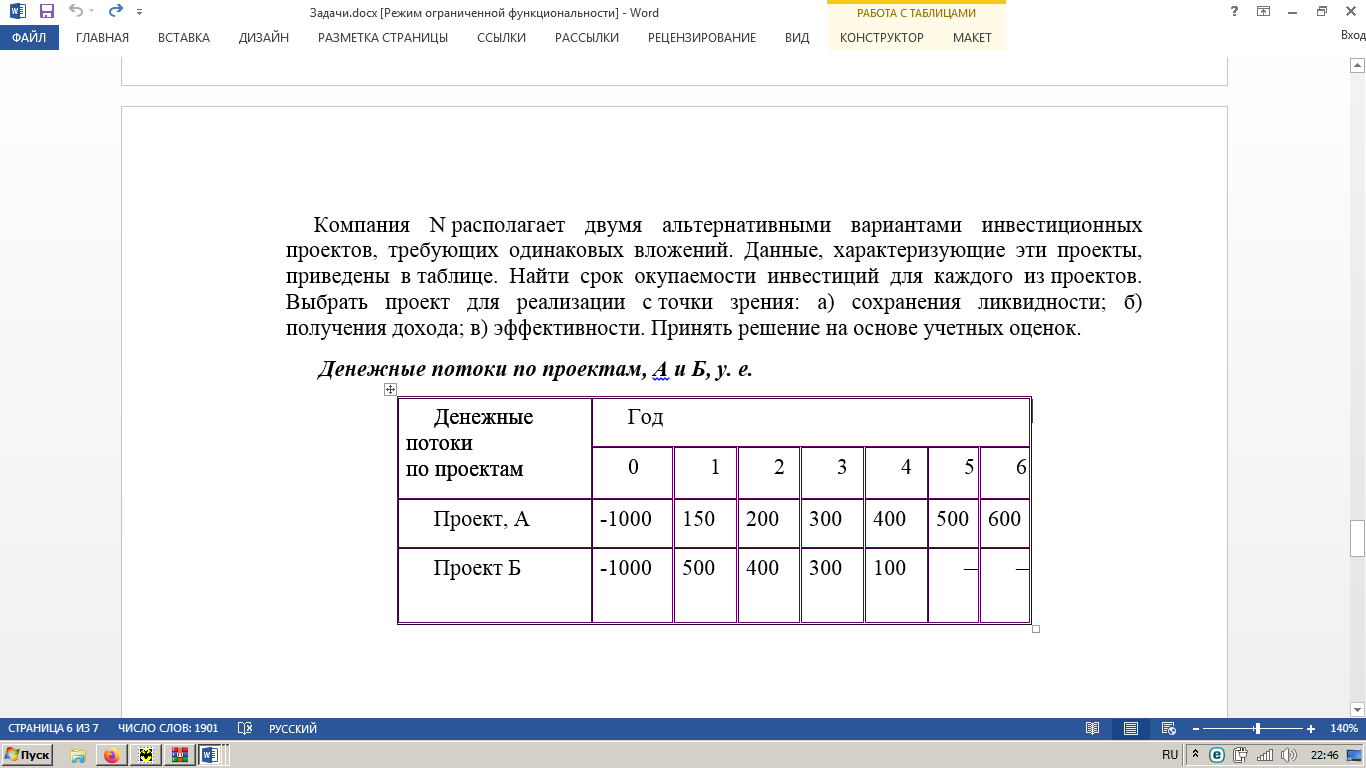 Решение: 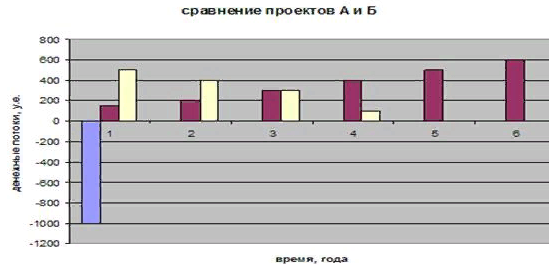 Рис.1 — денежные потоки по проектам, А и Б: синим цветом обозначены вложения, коричневым — денежные потоки для проекта А; желтым — денежные потоки для проекта Б. 1. Решим задачу на основе учетных (не дисконтированных) оценок. Срок окупаемости проекта, А : Считаем сумму доходов нарастающим итогом до тех пор, пока она не превысит капиталовложения: сумма доходов за первые 3 года составляет 150 + 200 + 300 = 650 у. е., что недостаточно для покрытия инвестиций; сумма доходов за первые 4 года составляет 650 + 400 = 1050 у. е., что покрывает инвестиции с избытком, т. е. срок окупаемости, согласно формуле, — 4 года. Найдем более точно срок окупаемости: через 3 года непокрытый остаток капиталовложений (Кост) равен: Кост = K — (D1 + D2 + D3) = 1000 — 650 = 350 у. е., который может быть покрыт за 0,875 (350/400) четвертого года, т. е. за 10,5 (0,875 Таким образом, срок окупаемости проекта, А составляет 3 года и 10,5 месяца. Аналогичным образом находим срок окупаемости проекта Б — 3 года, а более точно: Кост = K — (D1 + D2) = 1000 — (500 + 400) = 100 у. е., который может быть покрыт за 0,33 (100/300) третьего года, т. е. за 4 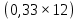 месяца. месяца.Таким образом, срок окупаемости проекта Б составляет 2 года и 4 месяца. Рассчитаем общий доход (D) по проектам: DA = 150 + 200 + 300 + 400 + 500 + 600 = 2150 у. е. DБ = 500 + 400 + 300 + 100 = 1300 у. е. Эффективность проекта можно оценить путем расчета коэффициента эффективности инвестиций, для чего необходимо рассчитать среднегодовую прибыль (Р) и среднегодовую стоимость эксплуатируемых инвестиций (I): PA = (DA — KA)/nА = (2150 — 1000)/6 = 191,7 у. е. PБ = (DБ — KБ)/nБ = (1300 — 1000)/4 = 75 у. е. Среднегодовая стоимость эксплуатируемых инвестиций у обоих проектов одинаковая: I = K/2 = 1000/2 = 500 у. е. Коэффициент эффективности инвестиций: 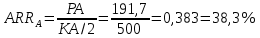 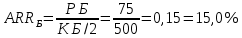 Ответ: С точки зрения ликвидности (по сроку окупаемости) более предпочтителен проект Б, окупающийся через 2 года и 4 месяца, чем проект, А, окупающийся за 3 года и 10,5 месяца. Однако проект, А приносит больше дохода (2150 у. е.), чем проект Б, (1300 у. е.) Проект, А также более эффективен 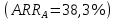 , чем проект Б , чем проект Б 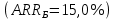 . .Вариант 3. Задача 1. Рассматривается вопрос о приобретении одной из двух машин, А и B. Ожидается, что их эксплуатация будет приносить доход в течение 2 и 3 лет соответственно (табл. 3.1.3). Альтернативные издержки равны 10 %. Вычислите чистую приведенную стоимость каждой машины. Какую машину следует купить? Таблица 3.1.3 — Потоки денежных средств для проектов А и В, руб. 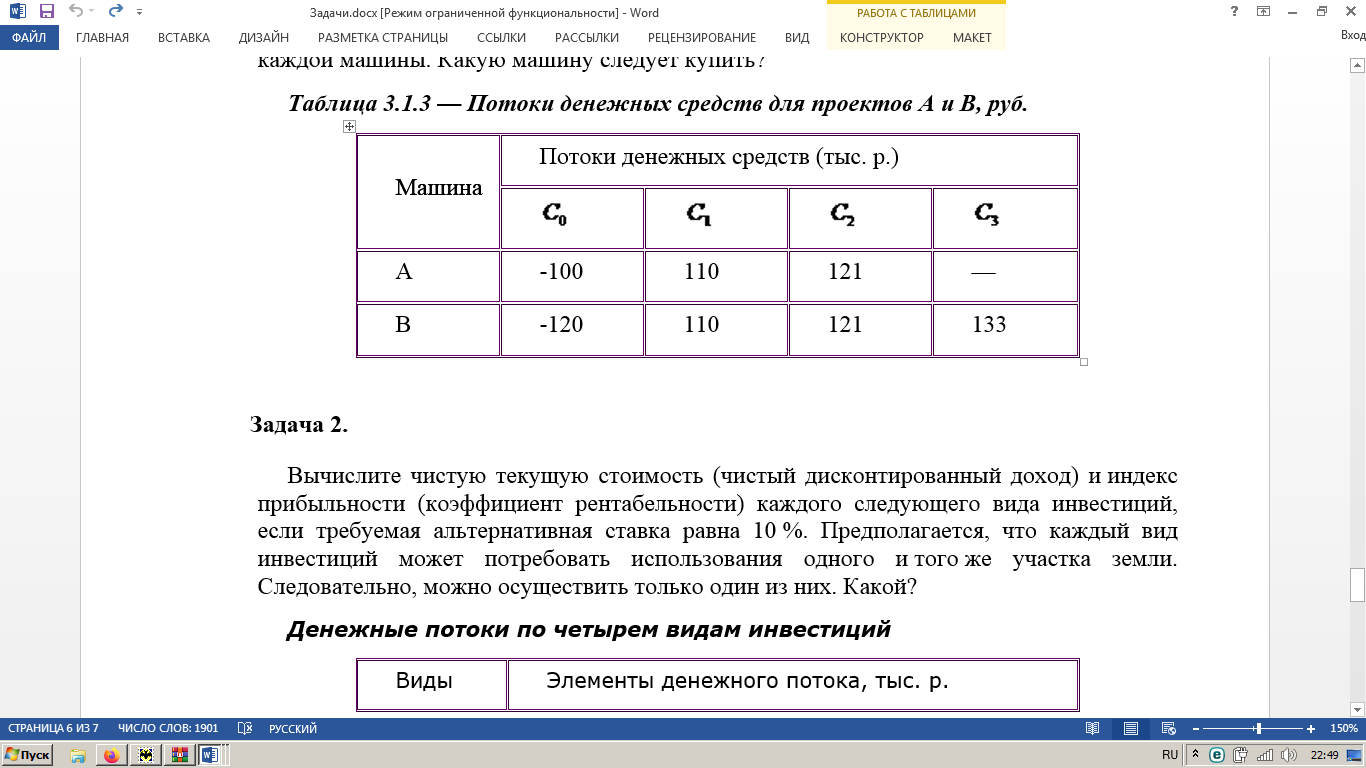 Решение: Используем стандартную формулу чистой приведенной стоимости: 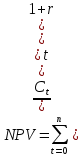 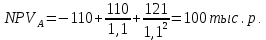 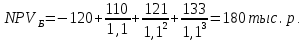 Исходя из показателя чистой приведенной стоимости, следует выбрать машину В, т. к. NPV у этого проекта больше. Однако следует помнить, что критерий NPV используется при сравнении ровно масштабных проектов. Здесь проекты имеют разные масштабы как с точки зрения вложений, так и срока эксплуатации. Поэтому необходимо привлечь критерий рентабельности инвестиций — PI: PI = PV / K = (NPV+K) / K. PI (A) = (100 + 100) / 100 = 2 = 200 %; PI (B) = (180 + 120) / 120 = 2,5 = 250 %. По данному критерию также следует отдать предпочтение проекту В. Ответ: Следует выбрать машину В. Задача 2. Вычислите чистую текущую стоимость (чистый дисконтированный доход) и индекс прибыльности (коэффициент рентабельности) каждого следующего вида инвестиций, если требуемая альтернативная ставка равна 10 %. Предполагается, что каждый вид инвестиций может потребовать использования одного и того же участка земли. Следовательно, можно осуществить только один из них. Какой? Денежные потоки по четырем видам инвестиций Элементы денежного потока тыс.руб.
Решение: Рассчитаем по стандартным формулам чистую приведенную стоимость и норму доходности (индекс прибыльности): 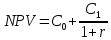 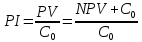 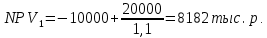 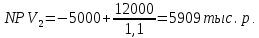 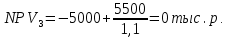 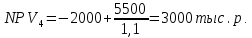 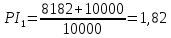 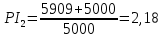 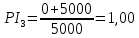 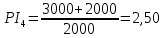 Ответ: Наибольшая чистая приведенная стоимость у первого проекта. Если мы хотим наращивать стоимость компании, то нужно выбрать проект 1, т. к. у него самая большая приведенная стоимость. А если нужно получить более высокую норму доходности, то проект 4, поскольку у него наибольший индекс прибыльности. Задача 3. У компании имеются два проекта -А и Б. Каждый проект имеет издержки в 10 тыс. р., альтернативные издержки для каждого проекта составляют 12 %. Ожидаемые денежные потоки, генерируемые этими проектами представлены в таблице 3.1.4. Денежные потоки по двум проектам, А и Б
Задания: а) подсчитать период окупаемости, чистую приведенную стоимость, коэффициент внутренней нормы доходности для каждого проекта; б) решить, какой проект должен быть принят, если они независимые; в) решить, какой проект должен быть принят, если они взаимоисключаемые; г) оценить, как изменение ставки дисконтирования могло бы привести к конфликту в ранжировании этих двух проектов по чистой приведенной стоимости и по внутренней норме доходности; Решение: а) 1. Расчет периода окупаемости. Окупаемость проекта, А (лет): 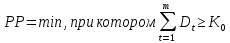 Т.к. ожидаемый поток доходов меняется из года в год, период окупаемости можно определить, суммируя доходы по годам до тех пор, пока их сумма не станет равной первоначальному вложению. Через 2 года накопленный доход 9,5 тыс. р. (6,5 + 3) меньше капвложений, через 3 года - 12,5 тыс. р. (6,5 + 3 + 3) — больше. Точный расчет срока окупаемости: 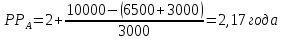 Аналогичный расчет сделаем для проекта Б. Окупаемость проекта Б (лет): 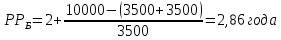 . .При независимости оба проекта следует принять, т. к. срок окупаемости не превышает срока эксплуатации проектов. Если следует выбрать один, то более предпочтительным оказывается проект, А, имеющий меньший срок окупаемости. 2. Чистая приведенная стоимость: 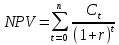 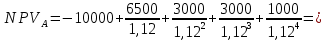 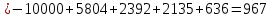 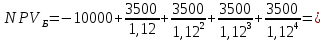 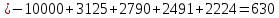 При независимости оба проекта следует принять, т. к. NPV для обоих проектов положителен. Если следует выбрать один, то более предпочтительным оказывается проект, А, имеющий больший чистый дисконтированный доход. 3. Внутренняя норма доходности: Для расчета внутренней нормы доходности воспользуемся приблизительным расчетом на основе формулы: 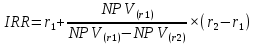 . .В качестве r1 используем исходную ставку дисконтирования 12 %. В качестве r2 возьмем, например, 20 %. Рассчитаем NPV со ставкой 20 %: 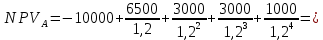 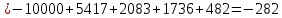 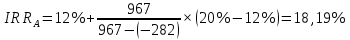 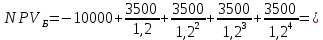 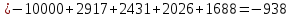 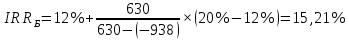 При независимости проекты следует принять, если PI не превышает стоимости привлекаемых средств. Если следует выбрать один, то более предпочтительным оказывается проект, А, имеющий большую внутреннюю норму доходности. б) По всем рассмотренным критериям оба проекта являются приемлемыми. Таким образом, оба проекта должны быть приняты, если они независимые. в) При альтернативности проектов выбрать следует проект А. Он лучше по всем показателям. г) Найдем r, при котором NPV двух проектов равны (точку Фишера): 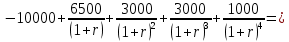 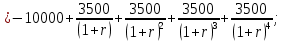 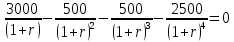 До множим обе части уравнения на 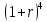 : :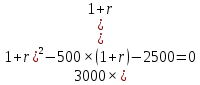 Подставим в левую часть r = 6 % и r = 7 %. В первом случае левая часть уравнения: 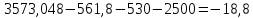 Во втором случае: 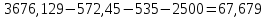 Теперь возьмем r=6,2% : 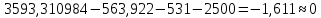 Поскольку существует точка Фишера, конфликт критериев при выборе инвестиционного проекта возможен. Если r < 6,2 %, то проект Б, худший по критерию IRR, оказывается лучшим по критерию NPV (см. рис. 2). 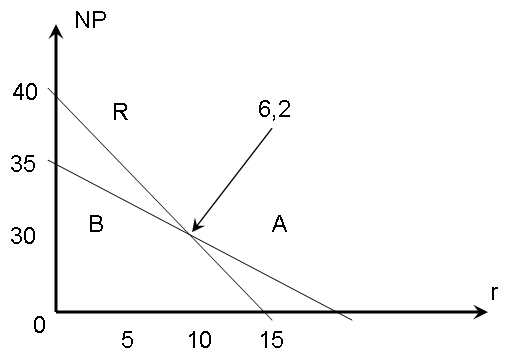 Рис. 2. Ответ: По всем рассмотренным критериям оба проекта являются приемлемыми. Таким образом, оба проекта должны быть приняты, если они независимые. Если проекты альтернативные, то выбрать следует проект А. |
