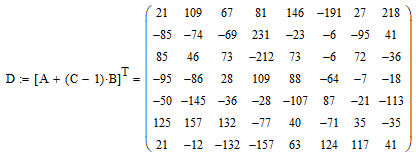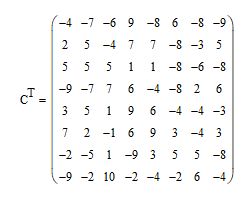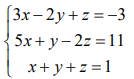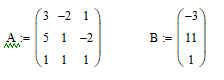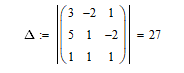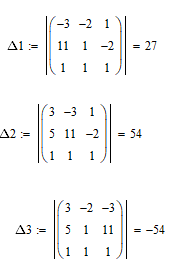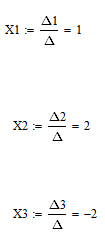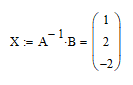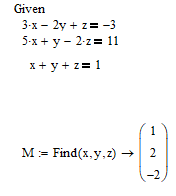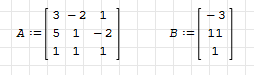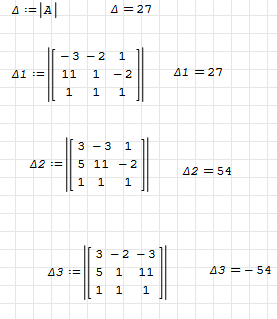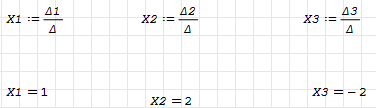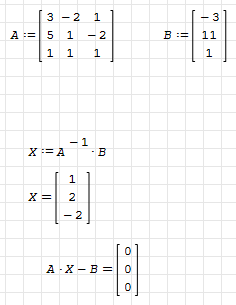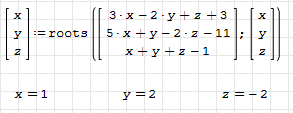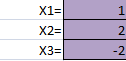Министерство науки и высшего образования Российской Федерации
ФГБОУ ВО
«Брянский Государственный
Технический Университет»
Кафедра «Информатика и программное обеспечение»
Курсовая работа
по курсу
«Информатика»
Тема: «Решение задач вычислительной математики с помощью универсальных и специализированных программ. Вариант 5»
Выполнил студент гр. О-20-МиР-мхт-Б
зач. книжка № 20.1177
________________________Иванова А.П.
«___» ____________2021г.
Проверил
_______________________асс. Лагерева Н.В.
«___» ____________2021г.
Брянск 2021
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ 3
1. ЗАДАНИЕ №1 4
1.1. Условие задания 4
1.2 Решение 5
1.2.1 Решение в MathCAD 5
1.2.2 Решение в SMath Studio 6
1.2.3 Решение в Excel 7
1.3 Вывод 7
2. ЗАДАНИЕ №2 11
2.1 Условие задания 11
2.2 Решение 12
2.2.1 Решение в MathCAD 12
2.2.2 Решение в Smath Studio 13
2.2.3 Решение в Excel 15
2.3 Выводы 16
3. ЗАДАНИЕ № 3 18
3.1 Условие задания 18
3.2 Решение 18
3.2.1 Решение в MathCAD 18
3.2.2 Решение в SMathStudio 20
3.2.3 Решение в MS Excel 21
3.3 Вывод 23
4. ЗАДАНИЕ №4 25
4.1 Условие задания 25
4.2 Решение 25
4.2.1 Решение в MathCAD 25
4.2.2 Решение в SMathStudio 25
4.2.3 Решение в MS Excel 26
4.3 Выводы 26
ЗАКЛЮЧЕНИЕ 26
СПИСОК ЛИТЕРАТУРЫ 27
ВВЕДЕНИЕ
Целью работы является закрепление и развитие навыков использования программных продуктов Excel, SMath Studio, Mathcad для решения некоторых задач вычислительной математики, которые понадобятся в процессе дальнейшего обучения в вузе и в профессиональной деятельности инженера, на основании таких заданий как:
· Исследование нелинейной функции одной переменной
· Работа с матрицами
· Решение систем линейных уравнений
· Приближение таблично заданной функции
Mathcad-инженерное математическое программное обеспечение, которое позволяет выполнять, анализировать важнейшие инженерные расчёты и обмениваться ими
SMath Studio — бесплатная программа для вычисления математических выражений и построения графиков функций. Работа с интерфейсом программы напоминает работу с обычным листом бумаги, так как все математические выражения в ней записываются не в строчку текстом, а в графическом, удобном для человека, виде.
MS Excel- программа для работы с электронными таблицами, созданная корпорацией Microsoft. Она предоставляет возможность экономико-статических расчётов, графические инструменты и язык макропрограммирования. MS Excel входит в состав Microsoft Office и на сегодняшний день MS Excel является одним из наиболее популярных приложений в мире.
1. ЗАДАНИЕ №1
1.1. Условие задания
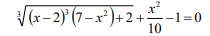
Диапазон изменения аргумента [-3;5]
Требуется:
1. Выполнить исследование нелинейного уравнения вида f(x)=0 (отыскать корни и экстремумы) с помощью программ Excel, SMath Studio и Mathcad. Для этого необходимо выполнить следующие действия:
· Провести табулирование функции f(x) на заданном интервале. Шаг табуляции h=0,2. Оформить таблицу (рамки, названия столбцов и т.п.).
· Построить график функции f(x).
· По графику определить приближенные значения корней уравнения f(x)=0 и точек экстремума функции. Этот этап называется «локализация корней и экстремумов». На нем необходимо обязательно задавать начальное приближение того значения аргумента, вблизи которого имеется корень или экстремум. В ходе последующего использования имеющихся процедур уточняется значение аргумента (соответствующего нужному корню или экстремуму). Поэтому для каждого корня или экстремума обязательно должно быть задано свое начальное приближение.
С помощью процедуры «Подбор параметра» определить уточненные значения корней уравнения f(x)=0.
Решить это же нелинейное уравнение с помощью программы Mathcad и SMath Studio. Для этого необходимо выполнить следующие действия:
· Построить график функции f(x).
· По графику определить начальные приближения корней уравнения f(x).
Для каждого приближения определить уточненные значения корней уравнения. Для этих целей могут быть использованы соответствующие функции: «root», «find» и т.п. Результат записать с точностью 2 знака после запятой.
С помощью символьных вычислений найти производную функции f(x). Найти экстремумы функции f(x) путем решения уравнения f'(x)=0.
Сравнить полученные результаты и сделать выводы об эффективности Excel, SМath Studio и Mathcad при решении задач нахождения корней нелинейного уравнения и поиска экстремумов функции
1.2 Решение 1.2.1 Решение в MathCAD
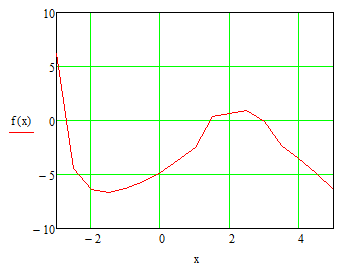 В данной программе построим график на интервале [-3;5] (см. рис. 1.1). И по этому графику определим приближенные значения корней. В данной программе построим график на интервале [-3;5] (см. рис. 1.1). И по этому графику определим приближенные значения корней.
Рисунок 1.1 График функции MathCAD
С помощью функции root находим точные значения корней x1= -2.642
X2= 1.346
X3= 3
X:= 0



При помощи функции Maximize находим точечные значения корней уравнения и экстремума функции
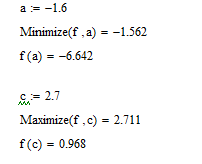
1.2.2 Решение в SMath Studio
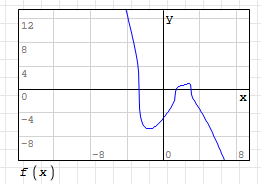 В данной программе построим график В данной программе построим график 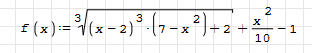 , на интервале [-3;5]. По графику определяем приближённые значения корней , на интервале [-3;5]. По графику определяем приближённые значения корней
Рисунок 1.2 График функции в SMath Studio
 С помощью функции solve находим точные значения корней уравнения С помощью функции solve находим точные значения корней уравнения
После этого найдём производную данной функции и построим график (см. рис 1.3)
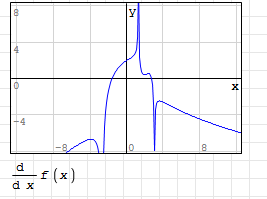 Рисунок 1.3 График производной функции в SMathStudio Рисунок 1.3 График производной функции в SMathStudio
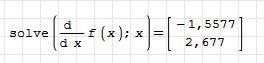 Для нахождения экстремума пользуемся функцией solve (см. рис 1.6) Для нахождения экстремума пользуемся функцией solve (см. рис 1.6)
Рисунок Рис 1.4 Экстремум функции
1.2.3 Решение в Excel
Построим таблицу, в которой укажем две колонки x и f(x) в первой колонке запишем значения от -3 до 5 с интервалом 0,2 А во второй колонке формулу которую опускаем до конца таблицы
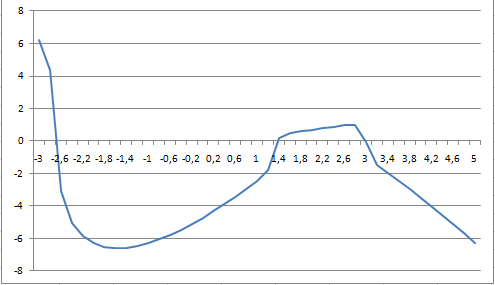 По этой таблице строим график (см рисунок 1.7) По этой таблице строим график (см рисунок 1.7)
Рисунок 1.5 График функции Excel
После этого находим корни с помощью «подбора параметра»
1.3 Вывод
Все результаты совпали, ответы везде одинаковые, хоть и решались различными способами в различных программах. Для работы с данными задачи лучше подходит MathCAD, так в нём много специальных функций для работы, SMath Studio так же подходит, но немного уступает выше сказанному. Excel же предназначен для выполнения совсем не таких операций. Ниже представлены все решения задач.
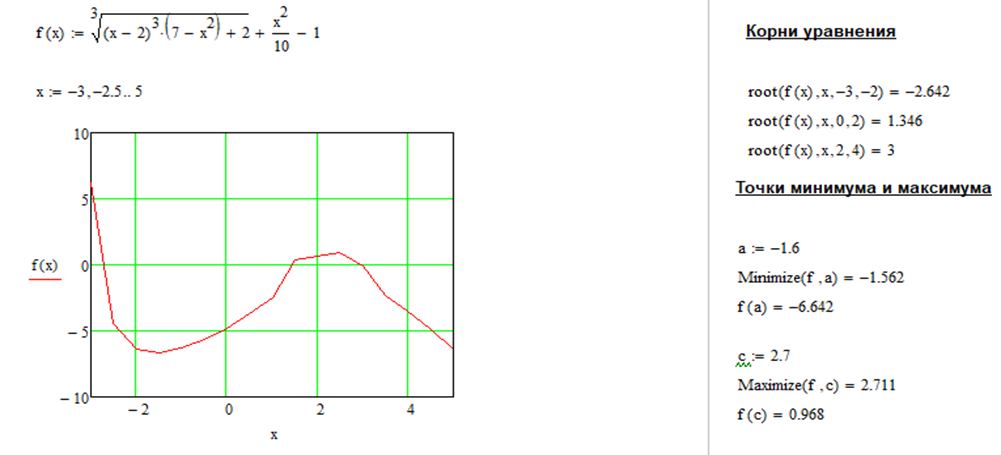 (cм рис 1.6-1.8) (cм рис 1.6-1.8)
Рисунок 1.6 Полное решение MathCAD
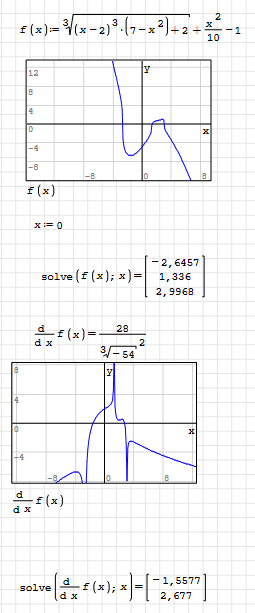 Рисунок 1.7 Полное решение SMathStudio Рисунок 1.7 Полное решение SMathStudio
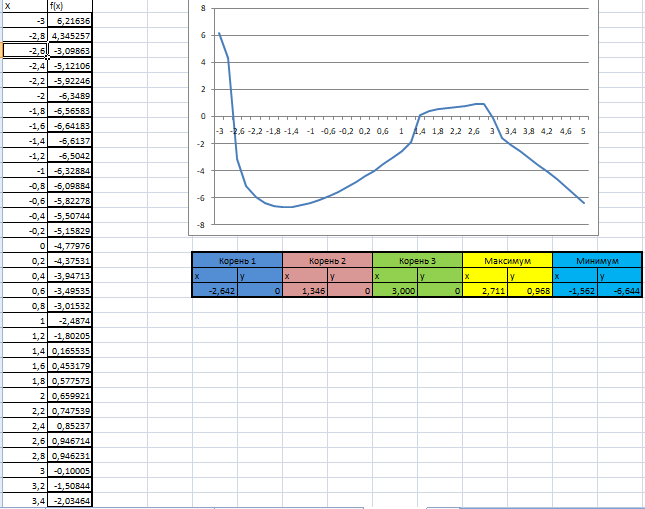
Рисунок 1.8 Полное решение Excel
2. ЗАДАНИЕ №2  2.1 Условие задания 2.1 Условие задания
Рисунок 2.1 Матрицы
Задания (cм рисунок 2.2)

Рисунок 2.2 Задания к выполнению
2.2 Решение 2.2.1 Решение в MathCAD
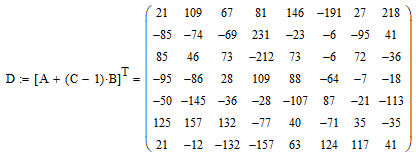 Запишем матрицы (см. рис 2.1) и дадим им названия, посчитаем значение D по формуле (см. рис 2.3) Запишем матрицы (см. рис 2.1) и дадим им названия, посчитаем значение D по формуле (см. рис 2.3)
Рисунок 2.3 Вычисление матрицы D
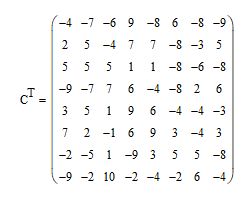 Сделаем транспортировку функции, для этого воспользуемся функциями MatchCad’а и выберем функцию транспортировки, получим результат (см. рис 2.4) Сделаем транспортировку функции, для этого воспользуемся функциями MatchCad’а и выберем функцию транспортировки, получим результат (см. рис 2.4)
Рисунок 2.4 Транспортировка Матрицы
 Найдём определитель матрицы с помощью тех же инструментов в панели (см. рис 2.5) Найдём определитель матрицы с помощью тех же инструментов в панели (см. рис 2.5)
Рисунок 2.5 Определитель Матрицы
Программа выдаст ошибку «Эта переменная не определена», так как можно находить определитель только для квадратной матрицы, которой матрица В не является.
 Найдём Обратную матрицу А воспользовавшись возведением её в -1 степень (см рис 2.6) Найдём Обратную матрицу А воспользовавшись возведением её в -1 степень (см рис 2.6)
Рисунок 2.6 Обратная матрица
Программа выдаст ошибку «Эта матрица должна быть квадратной», так как можно находить обратную матрицу только для квадратной матрицы, которой матрица А не является.
 При помощи команд raws и cols определим количество строк и столбцов соответственно (см рис 2.7) При помощи команд raws и cols определим количество строк и столбцов соответственно (см рис 2.7)
Рисунок 2.7 Кол-во строк и столбцов матрицы
При помощи команд submatrix можно определить кол-во строк и столбцов в матрицах (см. рис 2.8)

Рисунок 2.8 подсчёт строк в матрицах
2.2.2 Решение в Smath Studio
В данной программе использование функций совпадает с предыдущей программой


Рисунок 2.9 нахождение строк в матрицах
Единственное отличие заключается в том, что в SMath Studio при нахождении строки используется формула row, а не submatrix, как в MathCad (см рис 2.9)
2.2.3 Решение в Excel
Д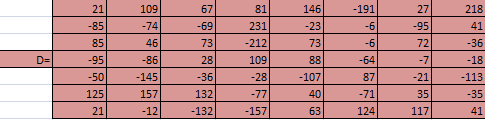
ля работы с матрицами в этой программе надо вписать числа в каждую ячейку, и для удобства можно присвоить имя каждой матрице
Рисунок 2.10 Вычисление матрицы D
Т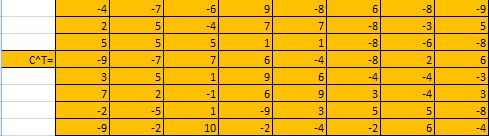
ранспортировка матрицы выполняется по формуле «ТРАНСП» (см. рис 2.11)
Рисунок 2.11 Транспортировка
О
пределитель находится по функции «МОПРЕД» (см. рис 2.12)
Рисунок 2.12 Определитель
Программа выдаст ошибку «Значение, используемое в формуле, имеет неправильный тип данных», так как матрица А не является квадратной.
О
братная матрица находиться по функции «МОБР» (см. рис 2.13)
Рисунок 2.13 Обратная матрица
Программа выдаст ошибку «Значение, используемое в формуле, имеет неправильный тип данных», так как матрица А не является квадратной.
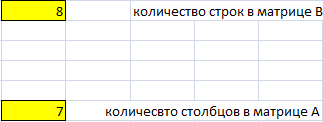 Число столбцов и строк у матриц в Excel’е определяется с помощью функций «ЧСТРОК» и «ЧИСЛСТОЛБ» соответсвенно (см рис 2.14) Число столбцов и строк у матриц в Excel’е определяется с помощью функций «ЧСТРОК» и «ЧИСЛСТОЛБ» соответсвенно (см рис 2.14)
Рисунок 2.14 Кол-во столбцов и строк
2.3 Выводы
Исходя из проделанной работы можно опять сказать? что программы Smath Studio и MathCAD подходят больше, потому что имеют больше функций и проще в использовании (см рис 2.15-2.17)

Рисунок 2.15 Полное решение MathCAD

Рисунок 2.16 Полное решение Smath Studio
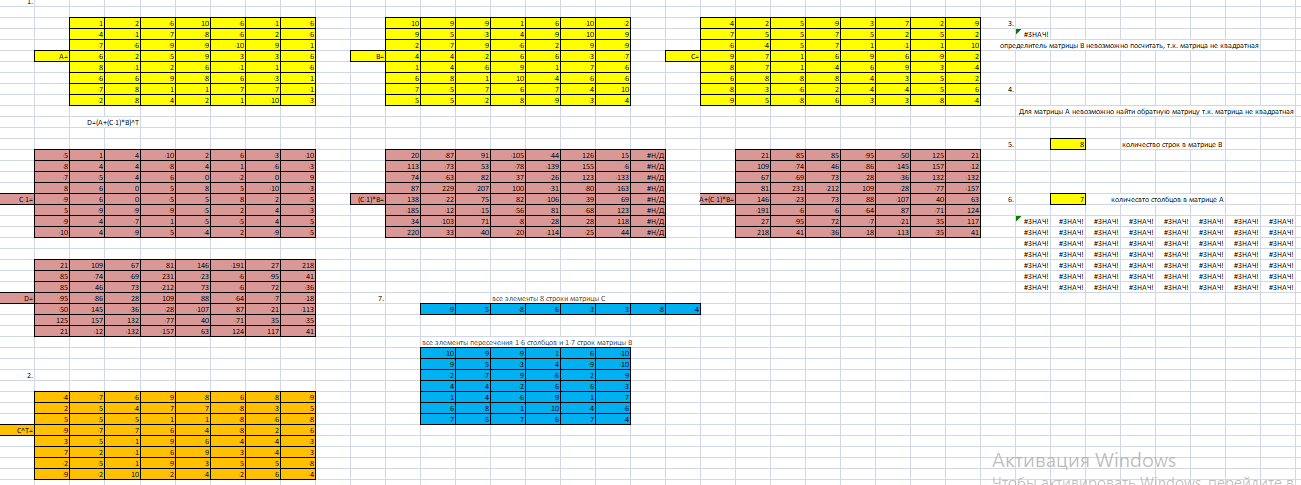
Рисунок 2.17 Полное решение Excel
3. ЗАДАНИЕ № 3 3.1 Условие задания
Решить систему линейных уравнений матричным методом, методом Крамера, итерационным методом в MathCAD, SMath Studio, MS Excel.
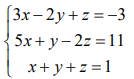
3.2 Решение 3.2.1 Решение в MathCAD
1)Метод Крамера
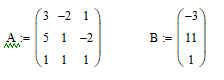 Запишем две матрицы A и B (см рис 3.1), после чего найдём определитель матрицы А (см. рис 3.2), достаточно выбрать в панели матриц, функцию определитель. Запишем две матрицы A и B (см рис 3.1), после чего найдём определитель матрицы А (см. рис 3.2), достаточно выбрать в панели матриц, функцию определитель.
Рисунок 3.1 Матрицы А и B
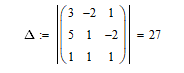
Рисунок 3.2 Определитель матрицы
Вычислим определители матриц, полученных заменой соответствующего столбца столбцом правых частей. Для того, чтобы найти определитель матрицы в MathCAD достаточно воспользоваться операцией «Определитель матрицы», которая находится в меню «Матрицы». MathCAD выполнит операцию и выдаст конечный результат (см рис 3.3)
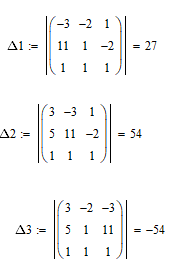 Рисунок 3.3 Определители Рисунок 3.3 Определители
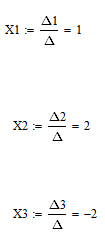 По формулам найдём решение системы (см рис 3.4) По формулам найдём решение системы (см рис 3.4)
Рисунок 3.4 Решение
2)Матричный метод
Введём матрицу и столбец правых частей. Для этого воспользуемся панелью инструментов «Матрицы и векторы». Обозначим матрицу, состоящую из коэффициентов за А, а матрицу из свободных членов – за B
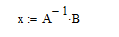
Потом выведем значения x
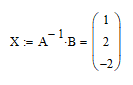
Таким образом, получили решение системы.
3) Итерационный метод
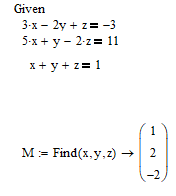
3.2.2 Решение в SMathStudio
1)Метод Крамера
Решение здесь будет такое же как в MathCAD
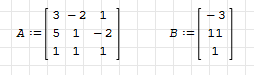 Запишем матрицы Запишем матрицы
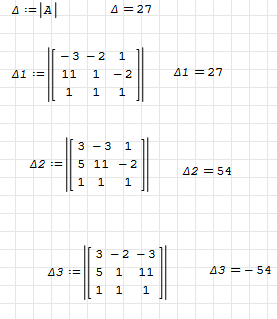 Найдём все определители (рис. 3.5) Найдём все определители (рис. 3.5)
Рис 3.5 Определители
Посчитаем их корни (рис. 3.6)
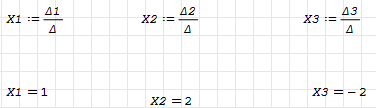 Рис. 3.6 Корни Рис. 3.6 Корни
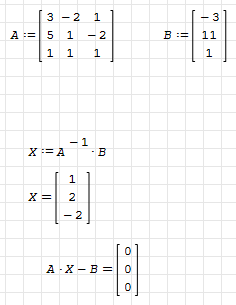 2)Матричный метод 2)Матричный метод
То же самое что и в MathCAD
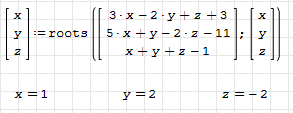 3)Итерационный метод 3)Итерационный метод
3.2.3 Решение в MS Excel
1)Метод Крамера
 Создадим две таблички, что и будет являться нашими матрицами Создадим две таблички, что и будет являться нашими матрицами
Находим определители (см рис 3.7), а затем и их корни (см. рис 3.8)
 Р Р
исунок 3.7 Определители
Рисунок 3.8 Корни
2)Матричный метод
П
о формуле =МОБР (C3:E5) высчитаем обратную матрицу (см рис 3.9) и умножим её на матрицу B, следовательно получим корни (см. рис 3.10)
Рисунок 3.9 Обратная матрица
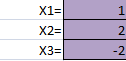
Рисунок 3.10 Корни
3)Итерационный метод
С
оздадим две матрицы. Первая – матрица коэффициентов. Вторая- матрица свободных членов. Присвоим первой матрице для удобства имя А, для второй – В.И пишем формулы «=СУММПРОИЗВ»
Затем выбираем «Поиск решения», в первой строке выбираем ячейку содержащую формулу 𝑓(𝑥)=СУММПРОИЗВ (C35:E35;$C40:$E40)
Во второй строке вводим значение первой строки матрицы В, в третьей строке выбираем зафиксированную ячейку $C40, нажимаем «найти решение
В таблице х4х5х6 делаем проверку результатов, для этого поочерёдно вычитаем из нужной ячейки матрицы В соответствующую ячейку таблицы, рассмотренной выше. В свободную ячейку вводим формулу для окончательной проверки ее значение должно быть равно нулю
3.3 Вывод
Результаты решений показаны ниже (см. рис.3.11-3.13) Ответы во всех программах сошлись. Наиболее удобной средой для работы с системами линейных уравнений является SMath Studio, т.к. она обладает набором специализированных инструментов для работы с матрицами, а также  удобные функции для вычисления. удобные функции для вычисления.
 Рисунок 3.11 Полное решение MathCAD Рисунок 3.11 Полное решение MathCAD
Рисунок 3.12 Полное решение SMath Studio
Р
исунок 3.13 Полное решение Excel
4. ЗАДАНИЕ №4 4.1 Условие задания
Решить задачу №1.18 (Волькенштейн с.18) в MathCAD, SMathStudio, MS Excel.
Поезд, двигаясь равнозамедленно, в течение времени t = 1 мин уменьшает свою скорость от v1 = 40 км/ч до v2 = 28км/ч. Найти ускорение a поезда и расстояние S, пройденное им за время торможения.
4.2 Решение 4
.2.1 Решение в MathCAD
4
.2.2 Решение в SMathStudio
4.2.3 Решение в MS Excel
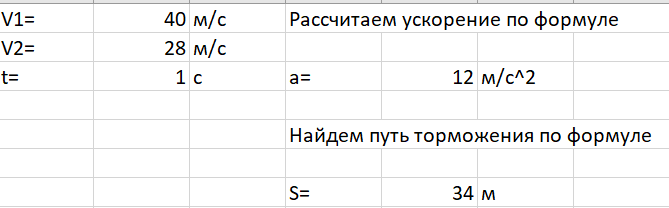
4.3 Выводы
Исходя из проделанной работы, можно сделать вывод, что такие программы как MathCAD и SMathStudio больше подходят для вычисления физических величин по формуле, нежели MS Excel. В данном случае функционал MS Excel менее удобный.
ЗАКЛЮЧЕНИЕ
В курсовой работе были изучены и закреплены навыки использования программных продуктов Excel, SMath Studio, Mathcad для решения некоторых задач вычислительной математики, которые понадобятся в процессе дальнейшего обучения в вузе и в профессиональной деятельности инженера, такие как:
Исследование нелинейной функции одной переменной
Работа с матрицами
Решение систем линейных уравнений
Приближение таблично заданной функции
Результаты, выполненных работ в 3х программа сошлись, в конце каждого задания можно было сравнить решение в каждой из программ.
Только в MathCAD получилось полностью выполнить все задания, в Smath Studio удобный интерфейс, но не хватает функционала, некоторые задания всё-таки удобнее было делать в Excel, где требовалось использование таблиц и графиков.
СПИСОК ЛИТЕРАТУРЫ
1. Поляков, В.П. Информатика для экономистов: практикум: учебное пособие для бакалавров / В.П. Поляков, В.П. Косарев, И.Ю. Прохина, В.И. Завгородский; под ред. В.П. Полякова, В.П. Косарева.-М.: ЮРАЙТ, 2013.-341 с.
2. Руководство по SMathStudio. – Режим доступа: https://sites.google.com/site/mikkhalichlab/rukovodstvo
3. Поляков, В.П. Информатика для экономистов: учебник для бакалавров / В.П. Поляков, Н.Н. Голубева, В.И. Завгородский, А.И. Кижнер; под ред. В.П. Полякова.-М.: ЮРАЙТ, 2013.-524 с.
4. Кирьянов, Д.В. MATHCAD 15 / MATHCAD PRIME 1.0.-СПБ.: БХВ-ПЕТЕРБУРГ, 2012.-432 с.
5. Трубников, С.В. Вычислительная математика: учеб. пособие / С.В.Трубников, Б.В. Порошин. – Брянск: БГТУ, 2005. – 396 с.
6. Понятный самоучитель Excel 2010. / В. Волков – С. П.: Питер, - 2010. – 252 с. –Режим доступа: rsload.net›knigi/8325…samouchitel-excel-2010.html
7. Виноградов, Ю.Н. Математика и информатика: учебник для среднего профессионального образования / Ю.Н. Виноградов, А.И. Гомола, В.И. Потапов, Е.В. Соколова.-4-е изд., стер.-М.: АКАДЕМИЯ, 2011.-271 с. |
 Скачать 0.6 Mb.
Скачать 0.6 Mb. В данной программе построим график на интервале [-3;5] (см. рис. 1.1). И по этому графику определим приближенные значения корней.
В данной программе построим график на интервале [-3;5] (см. рис. 1.1). И по этому графику определим приближенные значения корней.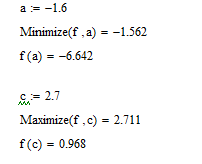
 В данной программе построим график
В данной программе построим график 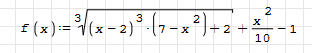 , на интервале [-3;5]. По графику определяем приближённые значения корней
, на интервале [-3;5]. По графику определяем приближённые значения корней С помощью функции solve находим точные значения корней уравнения
С помощью функции solve находим точные значения корней уравнения  Рисунок 1.3 График производной функции в SMathStudio
Рисунок 1.3 График производной функции в SMathStudio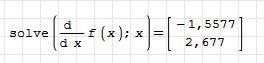 Для нахождения экстремума пользуемся функцией solve (см. рис 1.6)
Для нахождения экстремума пользуемся функцией solve (см. рис 1.6) По этой таблице строим график (см рисунок 1.7)
По этой таблице строим график (см рисунок 1.7) (cм рис 1.6-1.8)
(cм рис 1.6-1.8) Рисунок 1.7 Полное решение SMathStudio
Рисунок 1.7 Полное решение SMathStudio