линейное программирование. Юрков ВЕ. Решение задачи линейного программирования Необходимо найти максимальное значение целевой функции f x
 Скачать 1.26 Mb. Скачать 1.26 Mb.
|
|
Решить задачу ЛП графически, симплекс-методом, в среде Microsoft Excel: 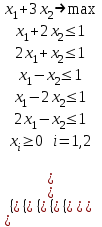 Графическое решение задачи линейного программирования Необходимо найти максимальное значение целевой функции F = x1+3x2 → max, при системе ограничений: x1+2x2≤1, (1) 2x1+x2≥1, (2) x1-x2≤1, (3) x1-2x2≤1, (4) x1 ≥ 0, (5) x2 ≥ 0, (6) Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом). 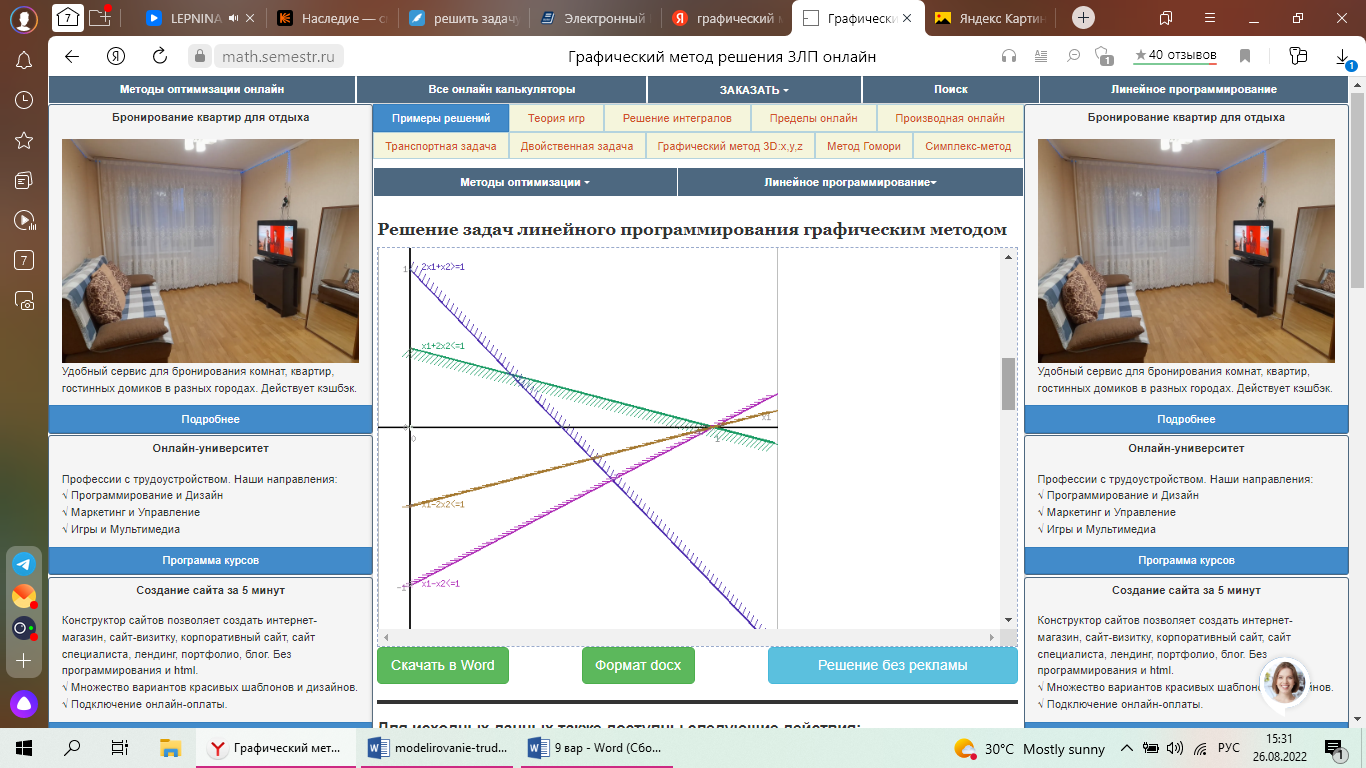 Границы области допустимых решений. Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи. Обозначим границы области многоугольника решений. 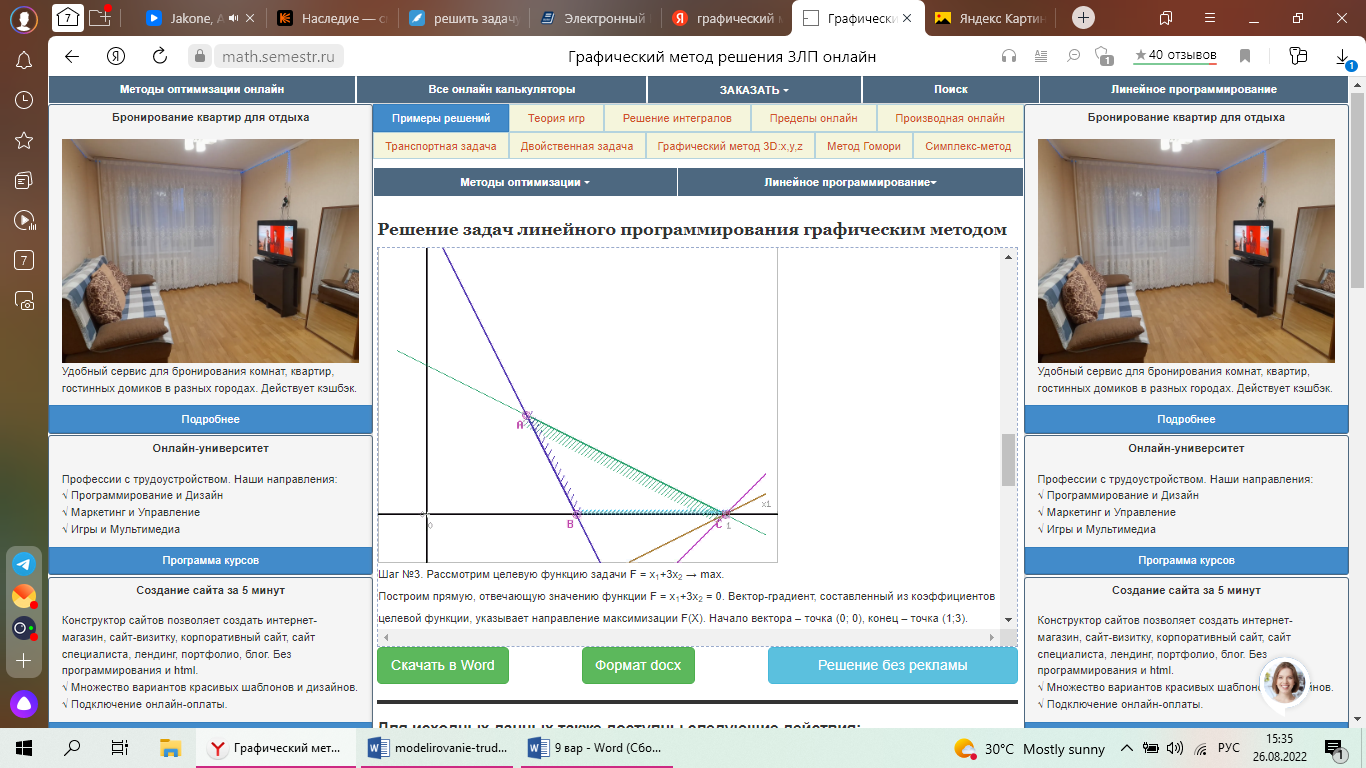 Рассмотрим целевую функцию задачи F = x1+3x2 → max. Построим прямую, отвечающую значению функции F = x1+3x2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (1;3). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией. 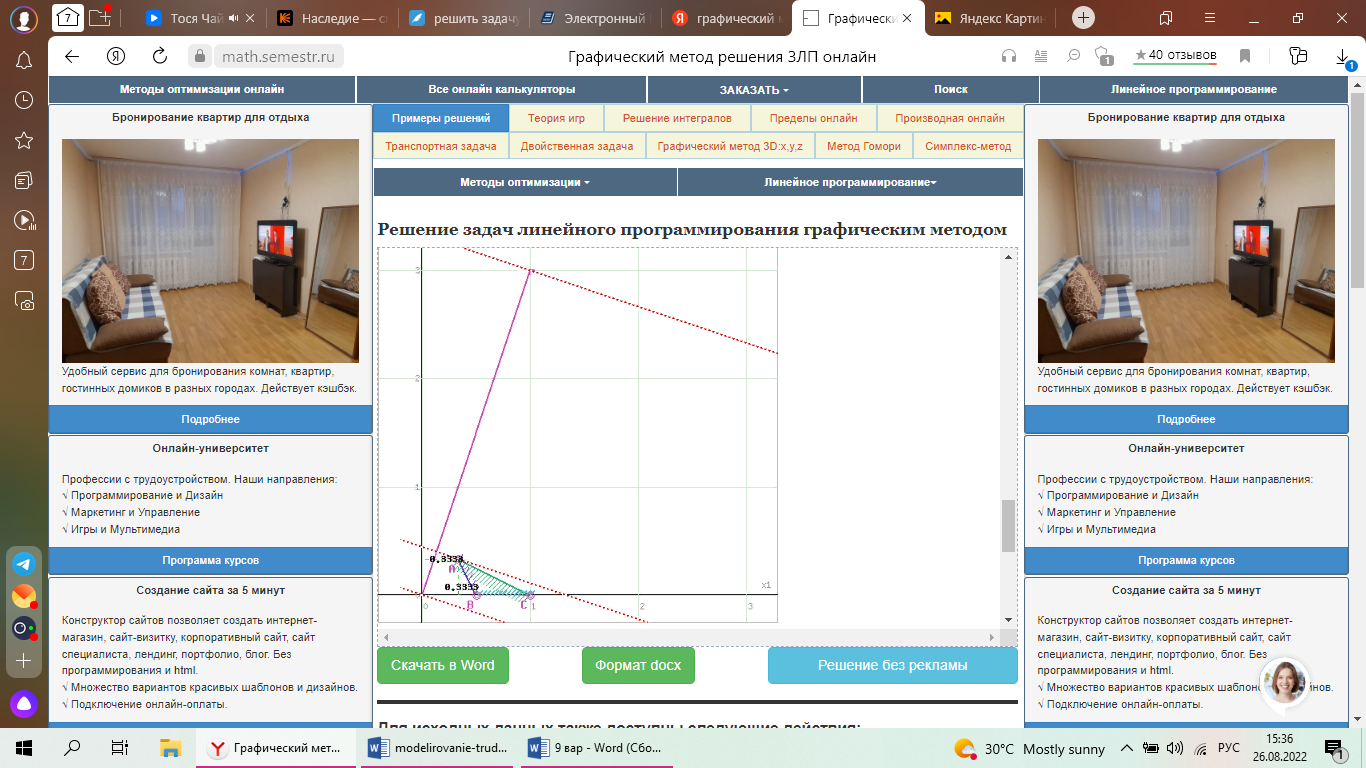 Прямая F(x) = const пересекает область в точке A. Так как точка A получена в результате пересечения прямых (1) и (2), то ее координаты удовлетворяют уравнениям этих прямых: x1+2x2=1 2x1+x2=1 Решив систему уравнений, получим: x1 = 0.3333, x2 = 0.3333 Откуда найдем максимальное значение целевой функции: F(x) = 1*0.3333 + 3*0.3333 = 1.3333 Решить эту же задачу с помощью надстройки «Поиск решения» в среде MSExcel 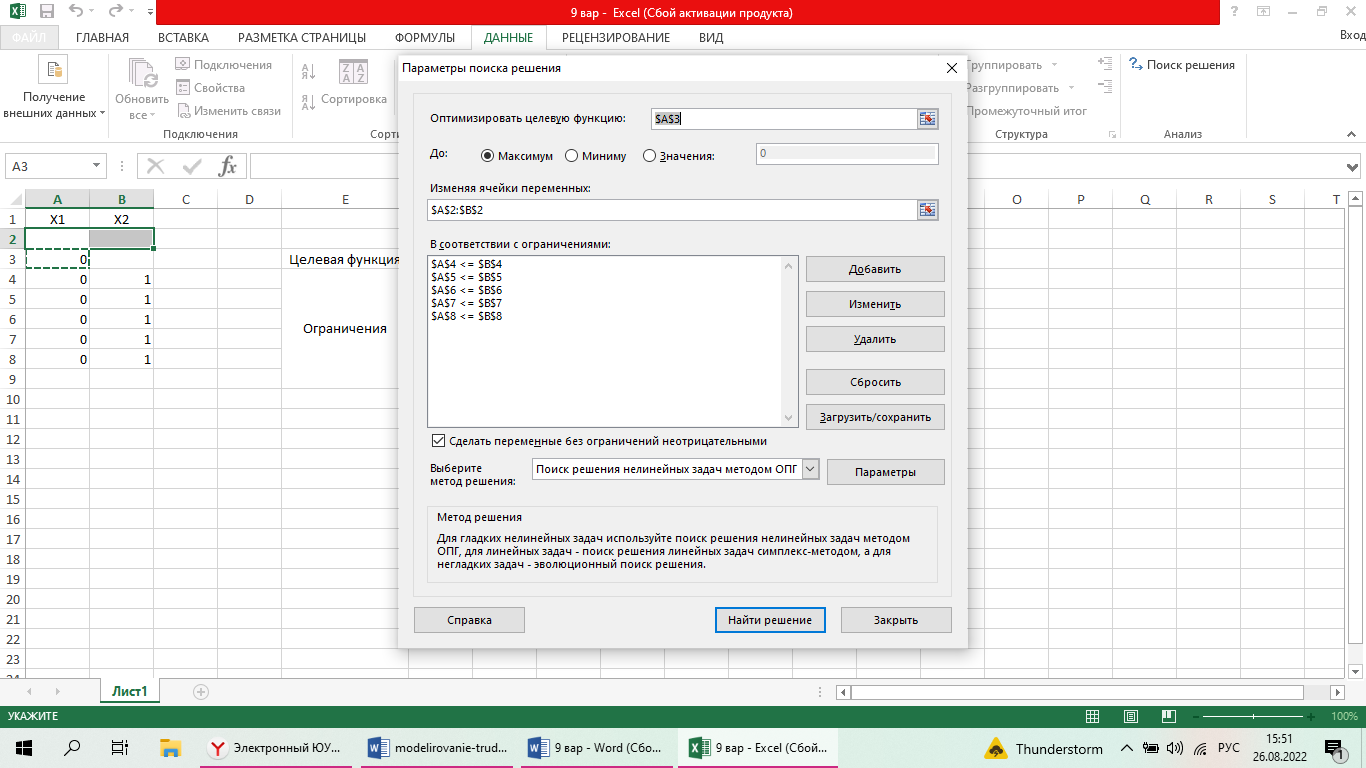  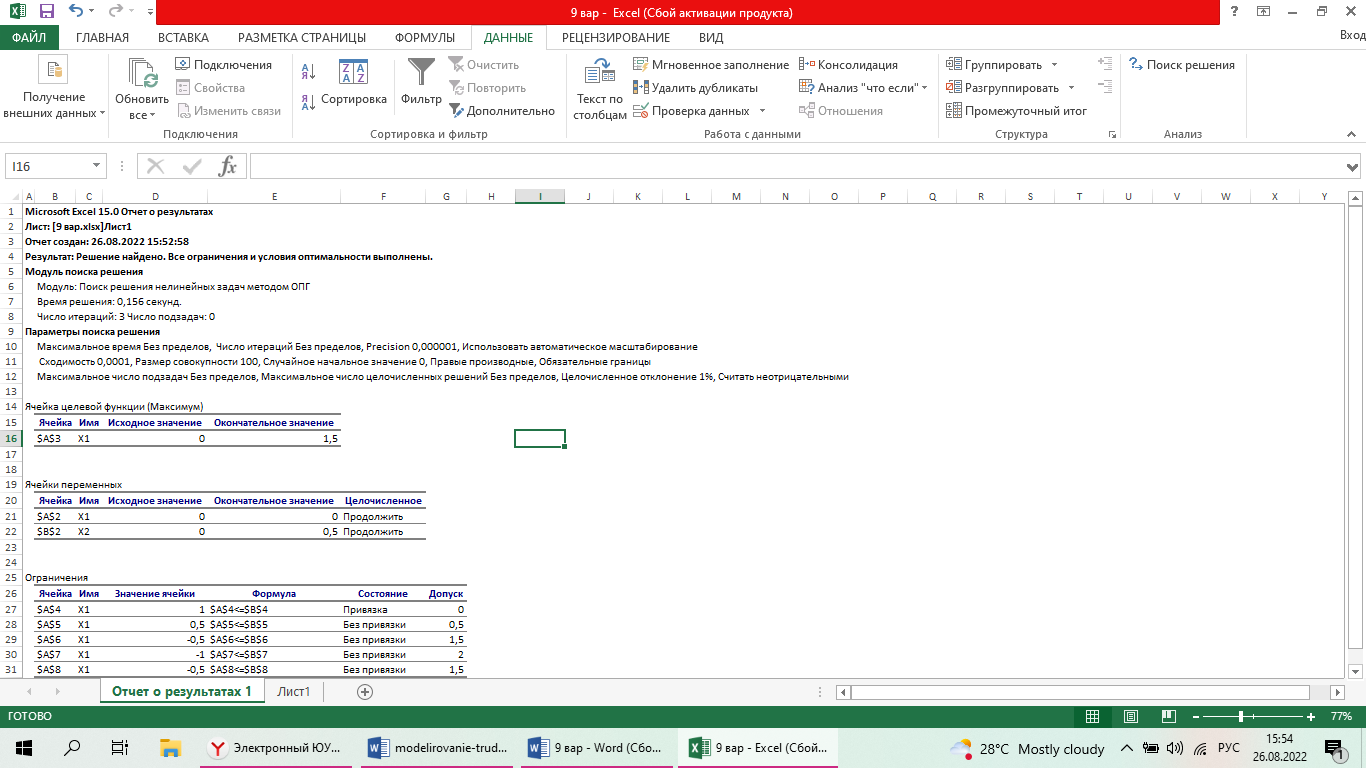 |
