Рубежный контроль аналетическая геометрия. Решение задачи выполнить и оформить в виде решения нижеследующих заданий
 Скачать 77.5 Kb.
|
|
Рубежный контроль по аналитической геометрии. Задача: В пространстве задана точка  своими координатами в прямоугольной системе координат, а также прямая линия своими параметрическими уравнениями.Найти координаты точки  с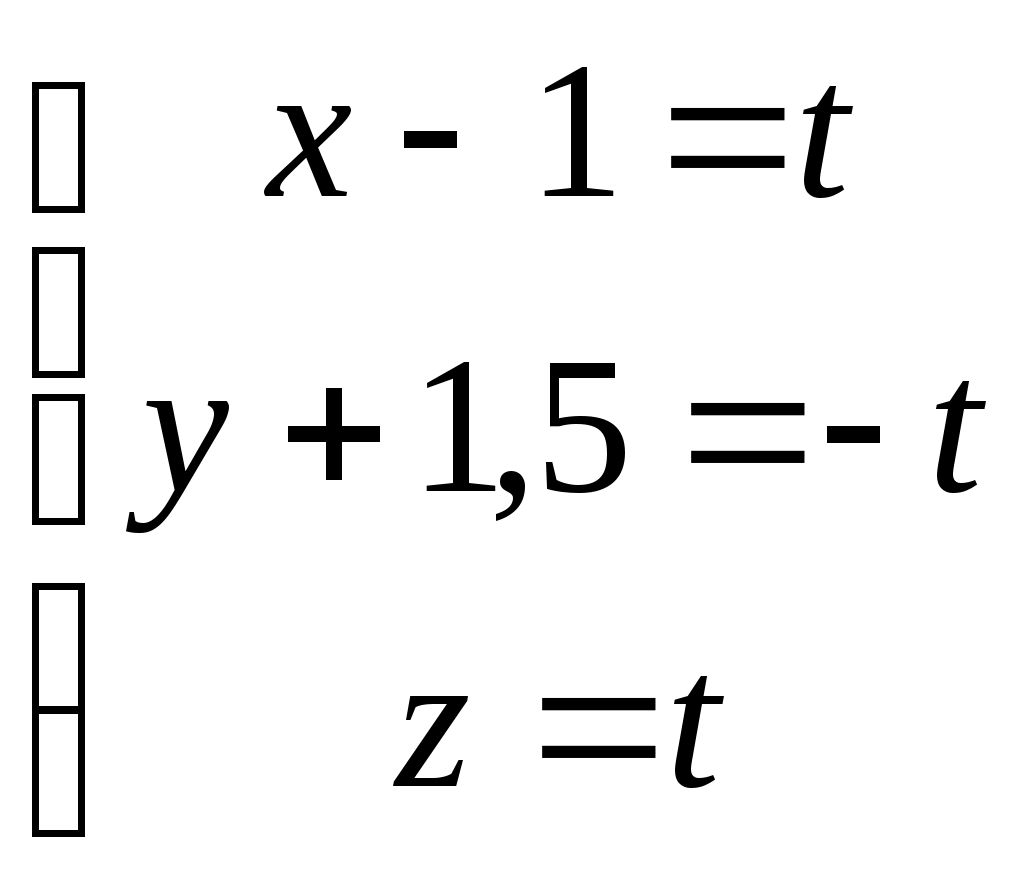имметричной точке М относительно заданной прямой.1)  ;  .2) 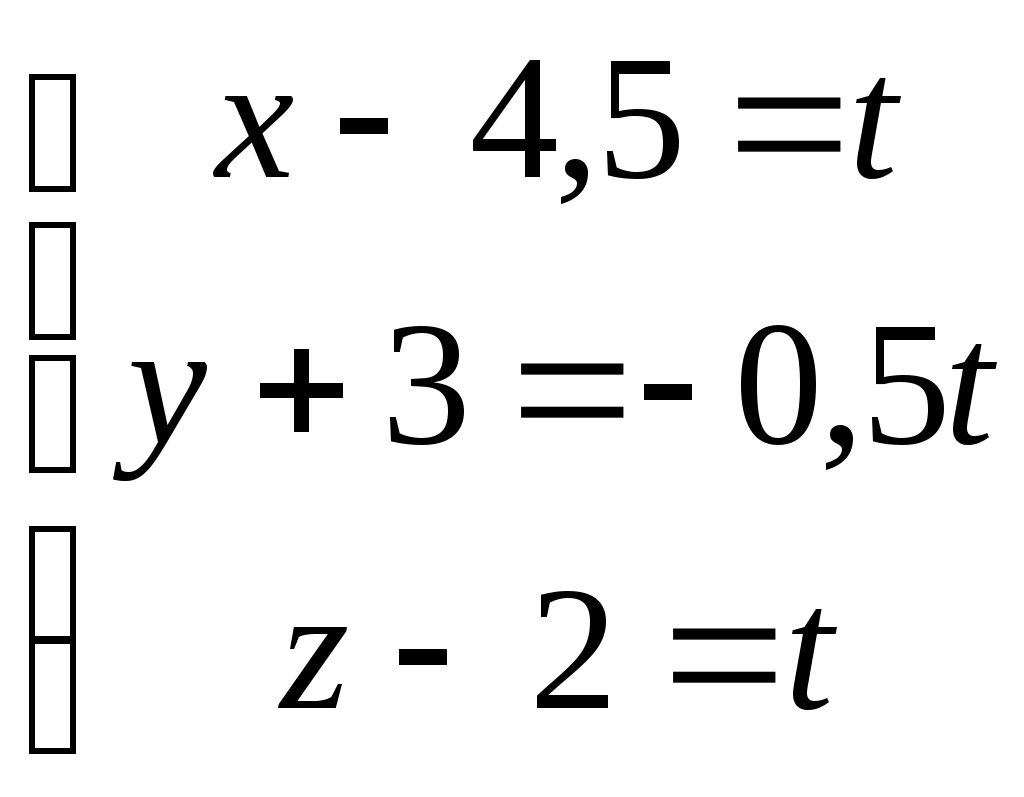 ;  .3)  ;  .4) 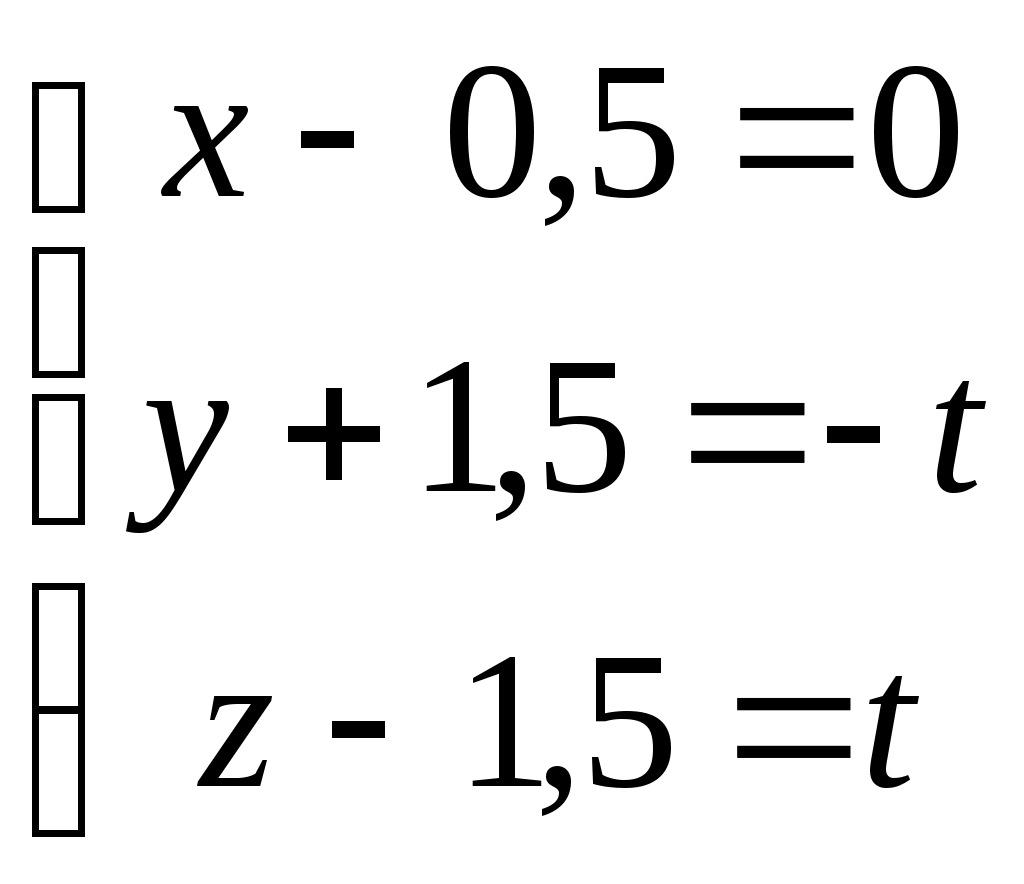 ;  .5) 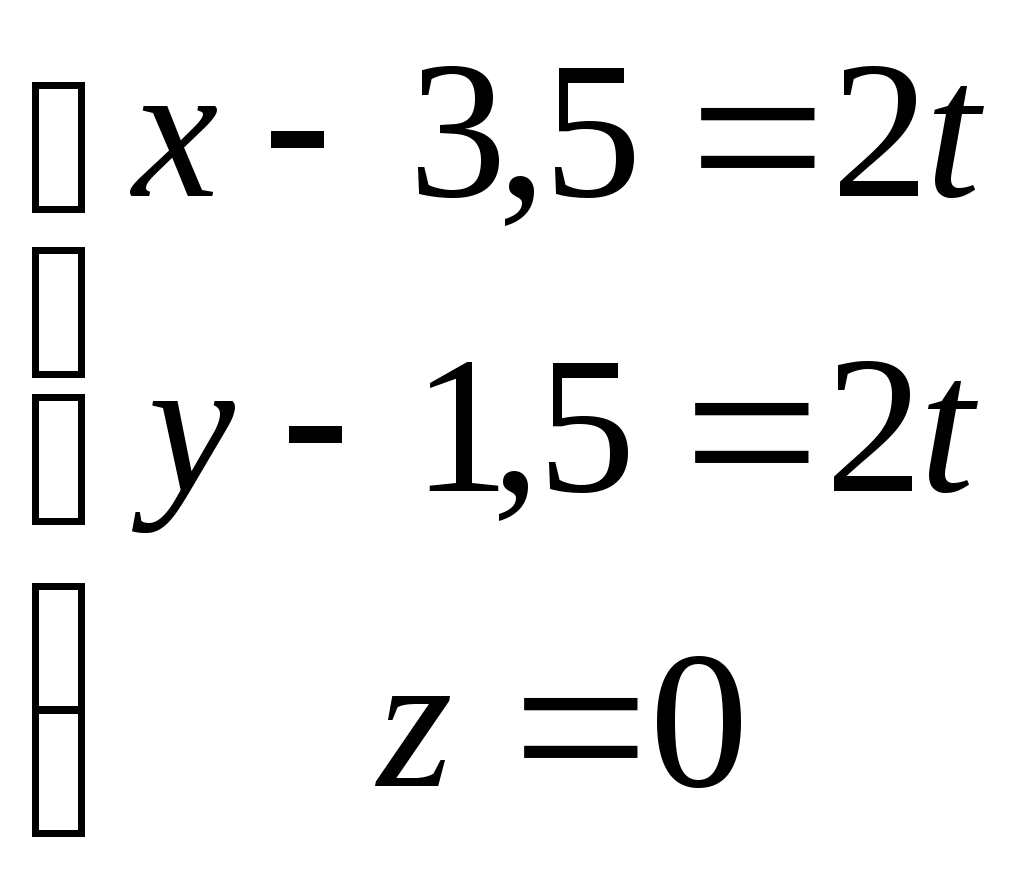 ;  .6) 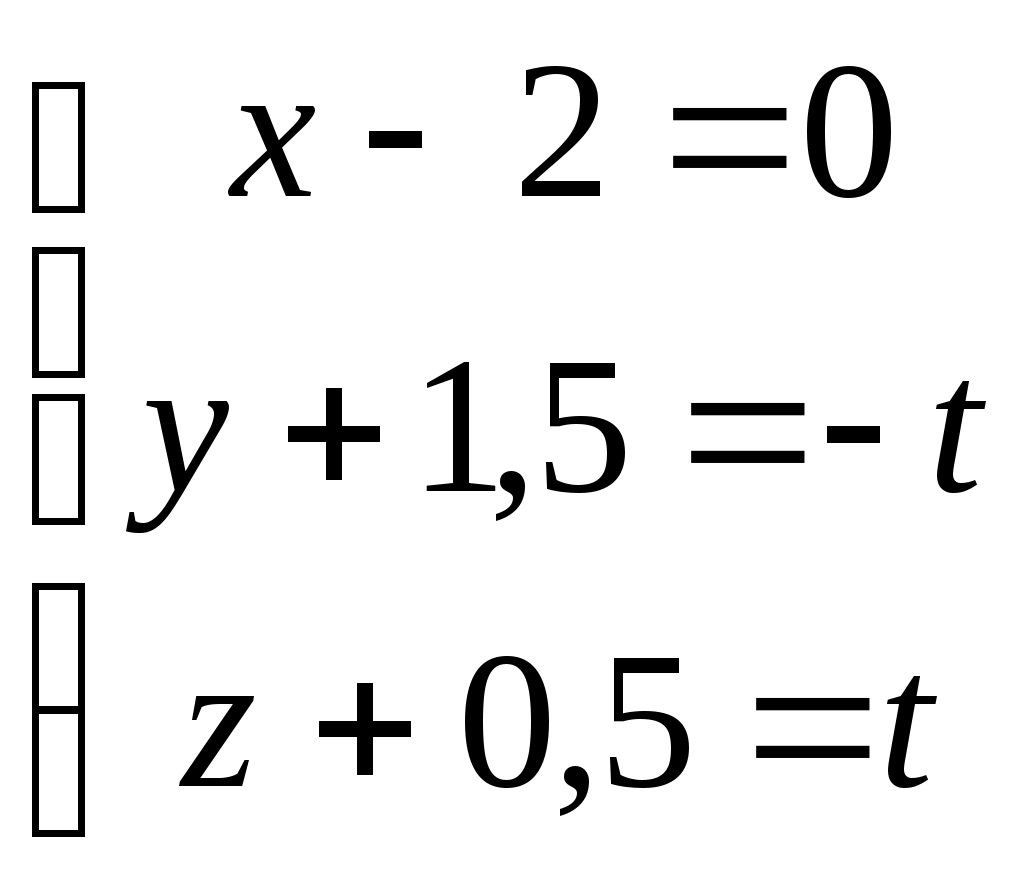 ;  .7) 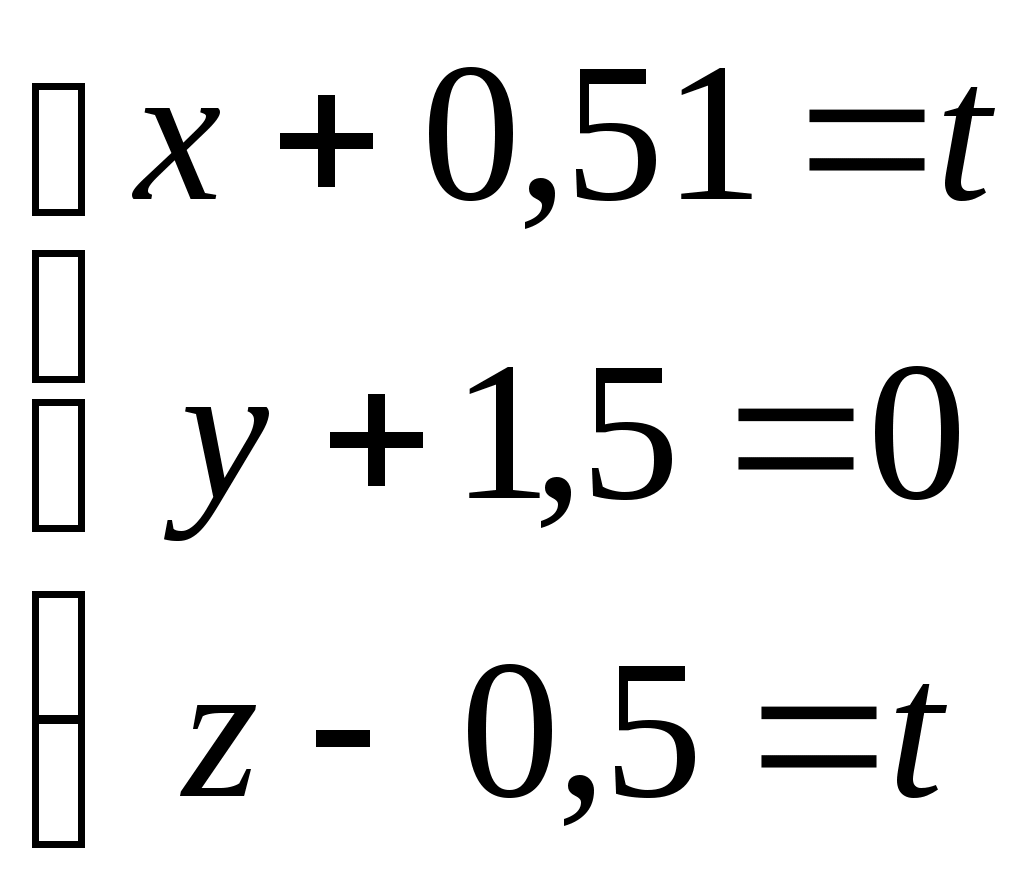 ;  .8)  ;  .9) 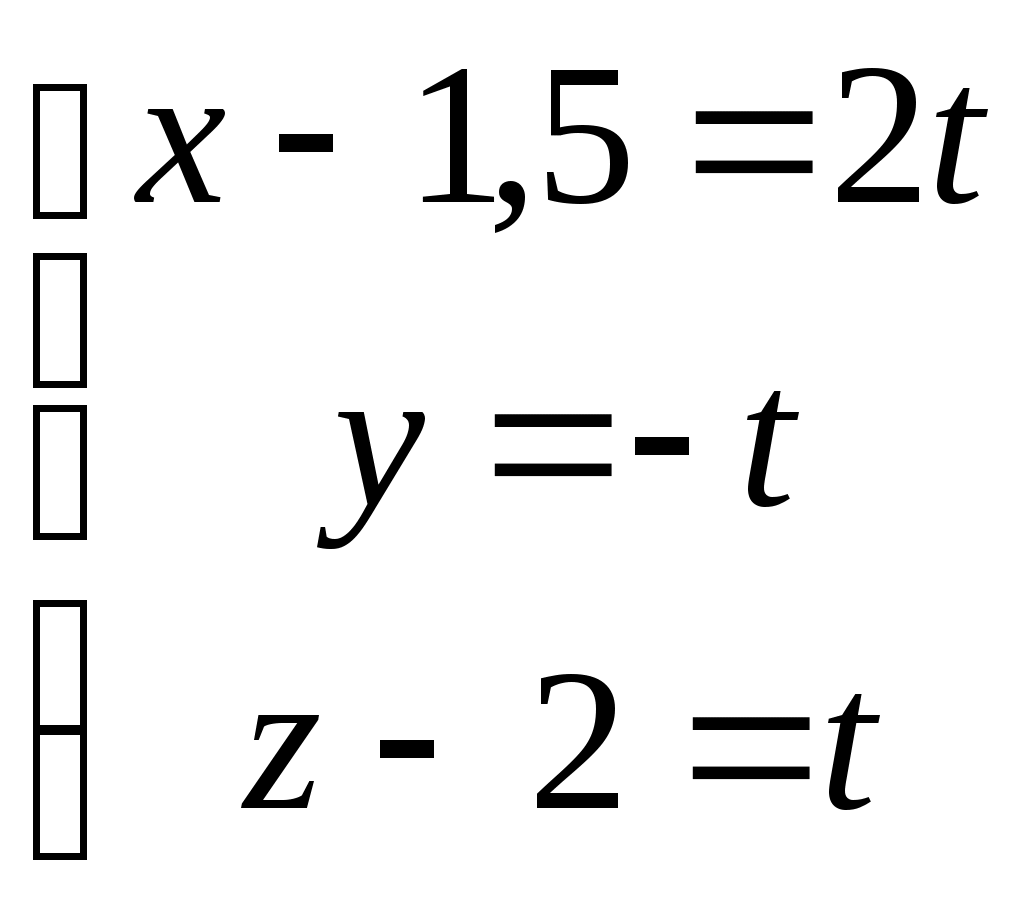 ;  .10) 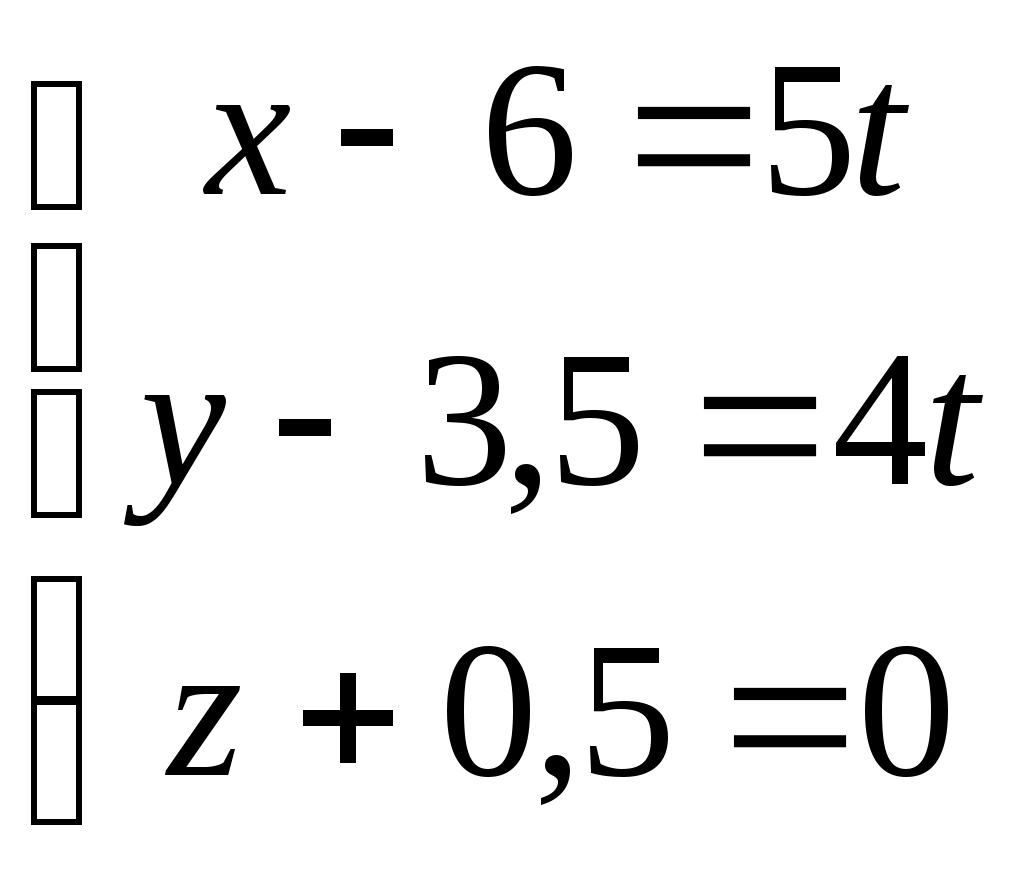 ;  .Дальше варианты заданий повторяются, т.е. вариант 11 такой же, как и 1, 12 такой же, как и 2, и т.д. Решение задачи выполнить и оформить в виде решения нижеследующих заданий: 1) Сделать схематический рисунок, на котором показать заданную точку М и заданную прямую.  2) Показать на рисунке направляющий вектор заданной прямой и выписать его координаты 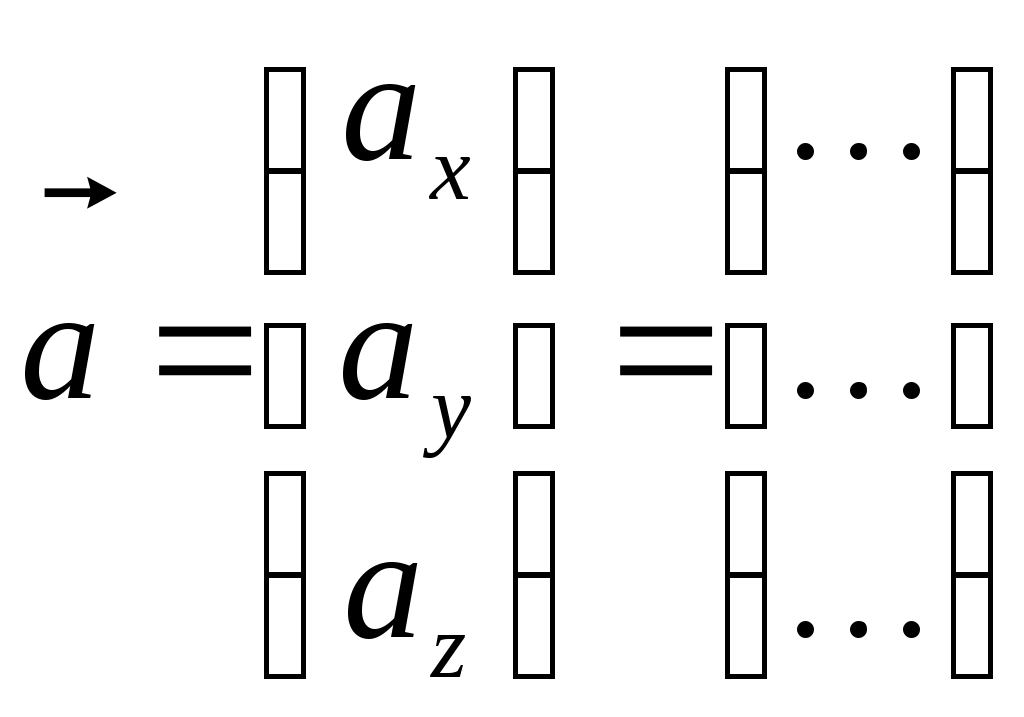 .Подсказка: Координаты направляющего вектора можно вычитать непосредственно из уравнений прямой. Это будут коэффициенты при переменной t в уравнениях этой прямой. 3) Показать на том же рисунке плоскость, проходящую через заданную точку М, перпендикулярно заданной прямой. Записать уравнение этой плоскости. Подсказка: В уравнении плоскости  ;коэффициенты при скобках являются координатами вектора нормали к плоскости. Но в условии задачи сказано, что плоскость должна быть перпендикулярна к заданной прямой. Поэтому направляющий вектор прямой одновременно оказывается нормальным вектором плоскости. Отсюда следует, что в качестве координат нормали можно взять координаты направляющего вектора прямой из п. 2, т.е. 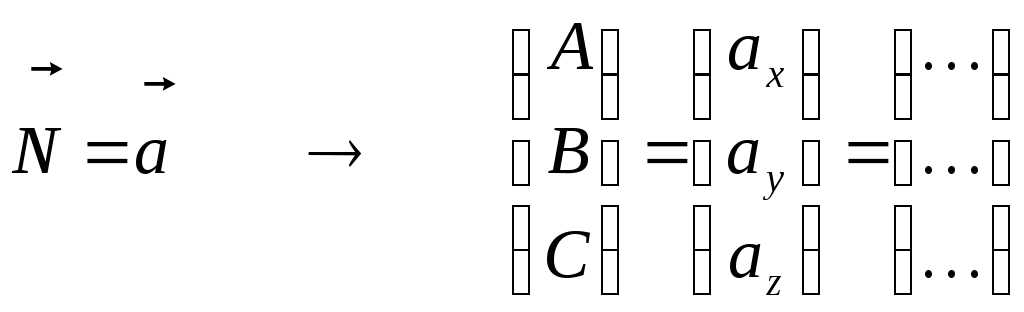 .Комментарии: Построенная плоскость будет проецирующей плоскостью, которая в пространственном случае помогает на практике произвести процедуру опускания перпендикуляра из заданной точки на заданную прямую. 4) Показать на рисунке точку К пересечения плоскости, построенной в п. 3, с заданной в условии задачи прямой. Найти координаты этой точки  .Подсказка: Координаты искомой точки пересечения должны удовлетворять и уравнению прямой, и уравнению плоскости. Следовательно, ее координаты можно найти как решения системы уравнений, составленной из уравнений прямой и добавленного к ним уравнения плоскости. Комментарии: Точка К является основанием перпендикуляра, опущенного из заданной точки на заданную прямую. 5) Показать на рисунке точку , симметричную заданной точке М относительно заданной прямой, и найти ее координаты.Указание: Из рисунка несложно увидеть, что  .Следовательно, координаты симметричной точки входят в это векторное уравнение в качестве искомых неизвестных. Остается решить это векторное уравнение относительно координат симметричной точки. |