эээж. олимп. Решение задачи выполняется от руки на листе бумаги
 Скачать 417.84 Kb. Скачать 417.84 Kb.
|
|
Муниципальный этап всероссийской олимпиады школьников по информатике Республика Алтай Задания и решения для 7-8 классов Ограничение по времени работы программы во задачах 4 и 5: 1 секунда. Эти задачи оцениваются в 100 баллов. Решение этих задач должно быть представлено в виде программы, которая считывает входные данные из текстового файла input.txt, а результат записывает в текстовый файл output.txt. Если решение проходит все тесты из условия, то оно принимается на проверку; если тест не пройден, решение не принимается на проверку и не будет оценено. Задача 1. Журнал Витя, Паша, Саша и Костя учатся в одном классе. В классном журнале они записаны под номерами 1, 2, 3 и 4 (в алфавитном порядке фамилий). Известно, что: 1) Витя и школьник с номером 3 — отличники; 2) Паша и школьник с номером 1 — троечники; 3) Школьник с номером 1 ростом выше школьника с номером 2; 4) Костя ростом ниже школьника с номером 2; 5) У Саши и Пети одинаковый рост. Определите, под каким номером каждый из школьников записан в классном журнале. Запишите ход решения задачи и ответ к ней в виде четырех цифр (без пробелов) — номера Вити, Паши, Саши, Кости. Например, ответ «4321» означает, что Витя в журнале идет четвертым, Паша — третьим, Саша — вторым, а Костя — первым. Решение задачи выполняется от руки на листе бумаги Система оценивания Задача оценивается максимум в 30 баллов при правильном ответе и записанном ходе решения. Отсутствие хода решения позволяет снизить балл до 25. Если в ответе правильно указаны номера двух мальчиков, то задача оценивается в 20 баллов. Если в ответе правильно указан номер только одного мальчика, то задача оценивается в 10 баллов. Ответ принимается на проверку, только если он является перестановкой чисел 1, 2, 3, 4, то есть ответ “1 1 1 1” недопустим. Решение Для решения задач такого типа удобно составить таблицу, в которой будем отмечать, кто кем быть не может, а кто кем быть может. Сверху запишем имена школьников, слева — их номера в журнале. В ячейки будем расставлять плюсы и минусы (если в ячейке П1 стоит минус, то это означает, что Пашин номер точно не 1). Сначала изобразим в таблице условие задачи. Поскольку Витя и школьник с номером 3 — отличники, то Витин номер точно не 3. Поскольку Паша и школьник с номером 1 — троечники, то Пашин номер — не 1 и не 3 (школьник с номером 3 — отличник) и Витин номер тоже не 1 (ведь он отличник). Из условий 3) и 4) следует, что Костин номер не 1 и не 2 (ведь он ниже). Последнее условие пока отмечать не будем.  Посмотрим на таблицу: в первой строке одна пустая клетка, следовательно, там должен стоять плюс, то есть, Сашин номер — 1 и в третьем столбце все остальные ячейки заполнены минусами. 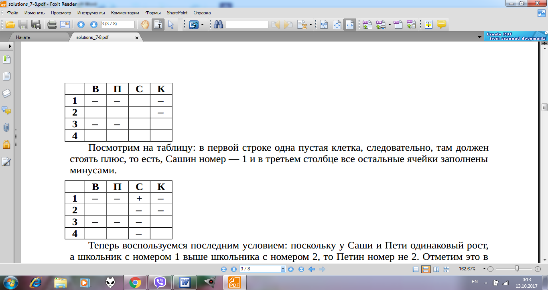 Теперь воспользуемся последним условием: поскольку у Саши и Паши одинаковый рост, а школьник с номером 1 выше школьника с номером 2, то Пашин номер не 2. Отметим это в таблице.  Тогда Пашин номер 4 и в четвертой строке все остальные ячейки заполнены минусами. Остались Витя и Костя - их номера 2 и 3.  Ответ:2413 Задача 2. Семизначное число Придумайте натуральное число, которое удовлетворяет следующим условиям: 1. Запись числа состоит из семи цифр. 2. Сумма всех цифр числа равна 39. 3. В записи числа есть хотя бы одна цифра 4. 4. В записи числа есть хотя бы одна цифра 7. 5. Запись числа является палиндромом, то есть одинаково читается как слева направо, так и справа налево (например, такими числами-палиндромами являются числа 121 и 7007, но не является число 1212). 6. Число является максимальным из всех чисел, удовлетворяющих пунктам 1-5. В ответе запишите придуманное вами число и придуманный вами способ получения числа. Решение задачи выполняется от руки на листе бумаги Система оценивания Задача оценивается максимум в 30 баллов. Для получения балла по задаче необходимо записать число, которое удовлетворяет как минимум 1-4 условиям. В этом случае за решение ставится 10 баллов. Если удалось подобрать число удовлетворяющее пунктам 1-5, то решение оценивается в 20 баллов, пунктам 1-6 – в 30 баллов. Решение Семизначное число-палиндром состоит из трех цифр в начале числа, одной цифры посередине числа, и трёх цифр в конце числа, которые совпадают с первыми тремя цифрами. Сумма всех цифр числа равна 39, и поскольку число является семизначным числом-палиндромом, то посередине десятичной записи числа стоит нечетная цифра. Значит, цифра 4 не стоит в числе посередине, и в числе содержится минимум две цифры 4 (по одной цифре среди первых трёх и среди последних трёх цифр числа). На первое место в числе поставим цифру 9, как максимальную цифру. Поскольку 9 + 4 + 7 = 20, то цифра 7 не может встречаться среди первых трех цифр числа (сумма первых трех цифр числа не может быть больше 19), значит цифра 7 стоит посередине числа. Тогда сумма первых трех цифр числа равна (39 - 7) / 2 = 16, и поскольку две цифры из первых трех уже известны (это 9 и 4), то третья цифра из первых трех равна 3. Поэтому максимальное число, удовлетворяющее условиям, равно 9437349. Задача 3. Робот рисует узор Исполнитель Робот умеет перемещаться по лабиринту, начерченному на плоскости, разбитой на клетки. Между соседними (по сторонам) клетками может стоять стена, через которую Робот пройти не может. У Робота есть четыре команды перемещения на одну клетку: вверх, вниз, влево, вправо. Если Робот получит команду передвижения сквозь стену, то он разрушится. Также у Робота есть команда закрасить, при которой закрашивается клетка, в которой Робот находится в настоящий момент. Составьте программу, с помощью которой Робот рисует узор (см. рисунок ниже). Начальное положение Робота левом верхнем углу. 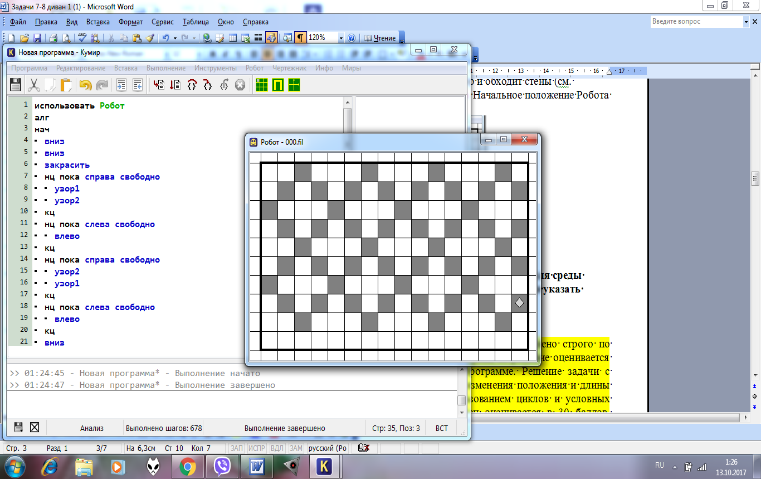 Решение_задачи_должно_быть_представлено_в_виде_файла_программы_для_среды_Кумир._Файл_необходимо_сохранить_в_папке_с_решениями_и_в_названии_указать_номер_задачи._Система_оценивания'>Решение задачи должно быть представлено в виде файла программы для среды Кумир. Файл необходимо сохранить в папке с решениями и в названии указать номер задачи. Система оценивания Задача оценивается максимум в 30 баллов. Если решение выполнено строго по приведенному рисунку с использованием линейного алгоритма, то решение оценивается максимум в 10 баллов, балл снижается за ошибки в программе. Решение задачи с использованием циклов и условных операторов оценивается в 20 баллов. Решение задачи с использованием циклов и условных операторов, и вспомогательного алгоритма оценивается в 40 баллов. Решение Один из вариантов решения с использованием вспомогательного алгоритма использовать Робот алг нач вниз вниз закрасить нц пока справа свободно узор1 узор2 кц нц пока слева свободно влево кц нц пока справа свободно узор2 узор1 кц нц пока слева свободно влево кц вниз вниз вниз закрасить нц пока справа свободно узор1 узор2 кц нц пока слева свободно влево кц нц пока справа свободно узор2 узор1 кц кон алг узор1 нач если справа свободно то вправо вверх закрасить если справа свободно то вправо вверх закрасить все все кон алг узор2 нач вниз если справа свободно то вправо закрасить вниз если справа свободно то вправо закрасить все все кон Задача 4. Лотерея в цветочном магазине В цветочном магазине лотерея. Каждому покупателю выдается еще один цветок в подарок. На круглой вращающейся полке стоят N горшков с цветами. Каждый горшок имеет порядковый номер от 1 до N. Покупатель, участвующий в лотерее, называет номер чека M и продавец считает по кругу горшки, начиная с горшка с номером 1. Тот горшок, на котором достигается число M, выдается покупателю. Определите номер цветочного горшка, который достанется покупателю. Программа получает на вход два целых положительных числа. Первое число N — количество горшков на полке. Второе число M — номер чека покупателя. Гарантировано, что M≥N (это условие проверять не нужно, в тестах к задаче оно учтено). Все числа не превосходят 2∙109. Программа должна вывести номер цветочного горшка, который получит покупатель. Пример входных и выходных данных
Решение задачи должно быть представлено в виде файла программы для среды программирования. Файл необходимо сохранить в папке с решениями и в названии указать номер задачи Система оценивания Задача оценивается максимально в 100 баллов. При решении задачи возможно использование стандартного потока ввода/вывода без использования текстовых файлов. Решение Ответом является остаток от деления числа M на число N, за единственным исключением – если остаток равен нулю, то есть M делится на N, то продавец остановит счет на последнем цветочном горшке с номером N и программа должна вывести значение N, а не 0. Это нужно рассмотреть при помощи одного условия if. Пример решения задачи на языке Free Pascal: program z04; var N,M:longint; input,output:text; begin assign(input, 'input.txt'); assign(output, 'output.txt'); reset(input); readln(input, N); readln(input, M); close(input); rewrite(output); if M mod N = 0 then writeln(output, N) else writeln(output, M mod N); close(output); end. Задача 5. Конвейер На конвейере три лотка с деталями. В левом лотке лежат X деталей, в среднем лежат Y деталей, в правом лежат Z деталей. Робот берет одну деталь из левого лотка, затем одну деталь из среднего лотка, затем из правого, среднего, левого, среднего, правого, среднего и т. д. (слева направо, затем справа налево, опять слева направо и т.д.) Если в каком-нибудь лотке детали кончились, робот останавливает конвейер и подает сигнал. Определите, сколько всего деталей возьмет робот до остановки конвейера. Программа получает на вход три целых положительных числа X, Y, Z – количество деталей в левом, среднем, правом лотке. Сумма трёх данных чисел не превосходит 2∙109. Программа должна вывести число деталей, которые возьмет робот до остановки. Пример входных и выходных данных
Решение задачи должно быть представлено в виде файла программы для среды программирования. Файл необходимо сохранить в папке с решениями и в названии указать номер задачи Система оценивания Задача оценивается максимально в 100 баллов. При решении задачи возможно использование стандартного потока ввода/вывода без использования текстовых файлов. Решение Решение, полностью моделирующее процесс взятия деталей роботом, то есть уменьшающее число деталей на 1 в каждом лотке в соответствии с описанным в условии алгоритмом, является слишком затратным по времени при больших значениях входных переменных. Для получения более быстрого решения заметим, что процесс взятия конфет содержит цикл «левый лоток, средний лоток, правый лоток, средний лоток», который затем повторяется. За один проход такого цикла число X уменьшается на 1, число Y уменьшается на 2, число Z уменьшается на 1. Посчитаем, сколько раз будет выполнен цикл — это минимум из чисел X, [Y / 2] и Z (под записью [Y / 2] подразумевается целая часть от деления Y на 2, то есть операция целочисленного деления). Запишем количество проходов цикла в переменную k и уменьшим значение переменных X и Z на k, а значение переменной Y на 2k. За k исполнений цикла суммарно будет взято 4k деталей. Следующий проход цикла не будет выполнен полностью. Посмотрим на значение переменных X, Y, Z в том порядке, в котором берутся детали из соответствующих лотков. Если X = 0, то нельзя на следующем шаге взять деталь из первого лотка, и ответом будет 4k. Если Y = 0, то будет взята деталь из первого лотка, но во втором лотке детали кончились, поэтому ответ будет 4k + 1. Если же Z = 0, то, аналогично, можно взять еще две детали из левого и среднего лотка, и ответ будет 4k + 2. Наконец, если все эти условия не выполнены, то ответ будет 4k + 3. Пример решения задачи на языке Free Pascal: program z05; var X,Y,Z,k: longint; input,output:text; begin assign(input, 'input.txt'); assign(output, 'output.txt'); reset(input); readln(input, X); readln(input, Y); readln(input, Z); close(input); rewrite(output); if X if kZ then k:=Z; writeln(k); X:=X-k; Y:=Y-2*k; Z:=Z-k; if X=0 then writeln(output, 4*k) else if Y=0 then writeln(output, 4*k+1) else if Z=0 then writeln(output, 4*k+2) else writeln(output, 4*k+3); close(output); end. |
