Решение Запишем матрицу в виде 3 4 2

• Название: Решение Запишем матрицу в виде 3 4 2
• Дата: 25.01.2022
• Размер: 93.69 Kb.
• Имя файла: 2211091.docx
• Тип: Решение; #341462
• страница: 2 из 2

Решение СЛАУ методом Гаусса.

Запишем систему в виде расширенной матрицы:

3 3 1 5 5 2 1 2 3

230 400 240

Умножим 1-ю строку на (5). Умножим 2-ю строку на (-3). Добавим 2-ю строку к 1-й:

0 0 -1 5 5 2 1 2 3

-50 400 240

Умножим 3-ю строку на (-5). Добавим 3-ю строку к 2-й:

0 0 -1 0 -5 -13 1 2 3

-50 -800 240

Теперь исходную систему можно записать так:

x₃ = -50/(-1)

x₂ = [-800 - ( - 13x₃)]/(-5)

x₁ = [240 - (2x₂ + 3x₃)]/1

Из 1-й строки выражаем x₃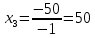



Из 2-й строки выражаем x₂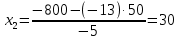



Из 3-й строки выражаем x₁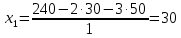


Задача 3.

Даны координаты вершин треугольника АВС. Найти:

1) длину стороны АВ.

2) уравнение стороны АВ и ее угловой коэффициент;

3) уравнение медианы, проведенной из вершины В;

4) уравнение высоты, опущенной из вершины С на сторону АВ;

5) уравнение окружности, для которой АВ – диаметр.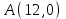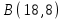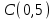

, ,

Решение: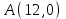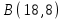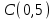

, ,

Координаты векторов находим по формуле:

X = x_j - x_i; Y = y_j - y_i;

здесь X,Y координаты вектора; x_i, y_i - координаты точки А_i; x_j, y_j - координаты точки А_j;

Например, для вектора AB

X = x₂ - x₁; Y = y₂ - y₁

X = 18-12 = 6; Y = 8-0 = 8

AB(6;8)

AC(-12;5)

BC(-18;-3)

1) длину стороны АВ.

Расстояние d между точками M₁(x₁; y₁) и M₂(x₂; y₂) определяется по формуле: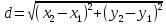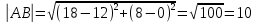





2) уравнение стороны АВ и ее угловой коэффициент;

Прямая, проходящая через точки A₁(x₁; y₁) и A₂(x₂; y₂), представляется уравнениями: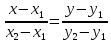



Уравнение прямой AB

Каноническое уравнение прямой: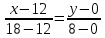



y = ⁴/₃x -16 или 3y -4x +48 = 0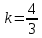



3) уравнение медианы, проведенной из вершины В;

Обозначим середину стороны AC буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам.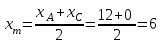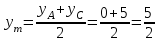





M(6;⁵/₂)

Уравнение медианы BM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана BМ проходит через точки B(18;8) и М(6;⁵/₂), поэтому:

Каноническое уравнение прямой: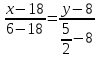



y = ¹¹/₂₄x ^-1/₄ или 24y -11x +6 = 0

4) уравнение высоты, опущенной из вершины С на сторону АВ;

Прямая, проходящая через точку N₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: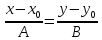



Найдем уравнение высоты через вершину C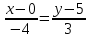



y = ^-3/₄x + 5 или 4y +3x -20 = 0

5) уравнение окружности, для которой АВ – диаметр.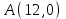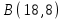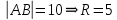

,



Обозначим середину стороны AB буквой O. Тогда координаты точки O найдем по формулам деления отрезка пополам.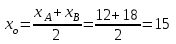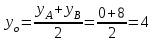





O(15;4)

Уравнение окружности с центром в точке О и радиусом 5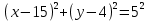



Задача 4.

Даны координаты точек 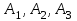, Найти:

1. 
   уравнение прямой ;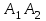
   
2. 
   уравнение плоскости ;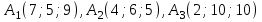
   

Решение:

Координаты векторов находим по формуле:

X = x_j - x_i; Y = y_j - y_i; Z = z_j - z_i

здесь X,Y,Z координаты вектора; x_i, y_i, z_i - координаты точки А_i; x_j, y_j, z_j - координаты точки А_j;

Например, для вектора A₁A₂

X = x₂ - x₁; Y = y₂ - y₁; Z = z₂ - z₁

X = 4-7; Y = 6-5; Z = 5-9

A₁A₂(-3;1;-4)

A₁A₃(-5;5;1)

1. 
   уравнение прямой ;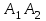
   

Прямая, проходящая через точки A₁(x₁; y₁; z₁) и A₂(x₂; y₂; z₂), представляется уравнениями: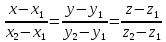



Уравнение прямой A₁A₂(-3,1,-4)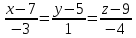

2. 
   уравнение плоскости ;
   

Если точки A₁(x₁; y₁; z₁), A₂(x₂; y₂; z₂), A₃(x₃; y₃; z₃) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:

x-x1 y-y1 z-z1 x2-x1 y2-y1 z2-z1 x3-x1 y3-y1 z3-z1

= 0

Уравнение плоскости A₁A₂A₃

x-7 y-5 z-9 -3 1 -4 -5 5 1

= 0

(x-7)(1·1-5·(-4)) - (y-5)((-3)·1-(-5)·(-4)) + (z-9)((-3)·5-(-5)·1) = 21x + 23y - 10z-172 = 0

Задача 5.

Выполните четыре арифметические действия над комплексными числами 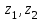, Найдите все значения .



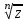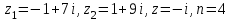Решение: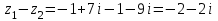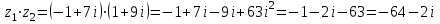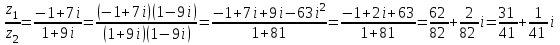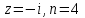











Действительная часть числа x. x = Re(z) = 0

Мнимая часть числа y. y = Im(z) = -1

Модуль комплексного числа |z|.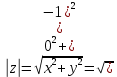



Поскольку x > 0, y < 0, то arg(z) находим как: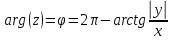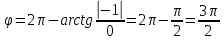





Таким образом, тригонометрическая форма комплексного числа z = -i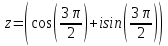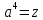





Извлекаем корни по формуле: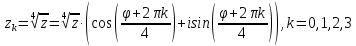



k = 0



k = 1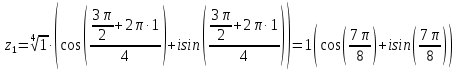



k = 2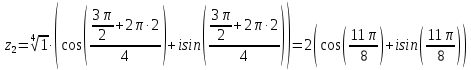



k = 3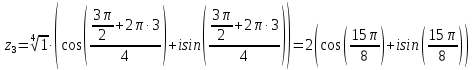



Задача 6.

Вычислить пределы.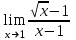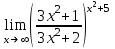



Решение: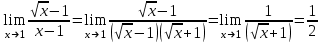





Задача 7.

Найти производную функции: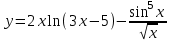



Решение: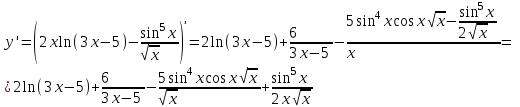



Задача 8.

Площадь, занимаемая печатным текстом, составляет на странице книги 432 см². Ширина полей вверху и внизу страницы по 2см, а ширина боковых полей по 1,5 см. Каковы должны быть размеры страницы, чтобы количество израсходованной на нее бумаги было наименьшим?

Решение:

Площадь текста S(t) = a*b = 432 кв.см.

Поля сверху и снизу - это 2 полоски шириной 2 см и длиной а см.

Поля слева и справа - это 2 полоски шириной 1,5 см и длиной b см.

Поля в углах (залиты красным) - это 4 прямоугольника 2 х 1,5 см.

Площадь полей S(p) = 2*2a + 1*1,5b + 4*2*1,5 = 4a + 3b + 12 кв.см.

Площадь листа выразим через одну переменную а

S = S(t) + S(p) = 432 + 4a + 3*432/a + 12 -> min

Возьмем производную от площади и приравняем ее к 0

S ' = 4 - 3*432/a² = 0

4 = 3*432/a²

a² = 3*432/4 = 3*3*144/4 = 3²*12²/2²

a = 3*12/2 = 36/2 = 18 см

b = 432/a = 432/18 = 24 см.

Размер листа

Длина a + 2*1,5 = a + 3 = 18 + 3 = 21 см

Высота b + 2*2 = b + 4 = 24 + 4 = 28 см.

Ответ: 21 х 28 см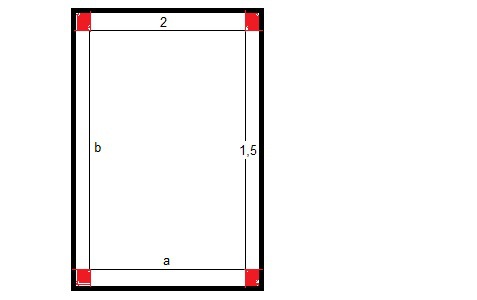


Список литературы.

1. 
   Выгодский М.Я. Справочник по высшей математике, М., АСТ Астрель, 2008 г;
   
2. 
   Гельфанд И.М. Лекции по линейной алгебре, М., Наука, 1998г;
   
3. 
   Курош А.Г. Курс высшей алгебры: Учебник для вузов. - М.: Физматкнига Лань, 2007г;
   
4. 
   Романова О. А. Математический анализ Справочное пособие для студентов экономических специальностей Иркутск 2003 . - Режим доступа http://matan.isu.ru/matan/.
   
5. 
   Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Учеб. для вузов: в 3-х томах. – 8-е изд.-М.: Физматлит. т.1 – 2001. -697 с.