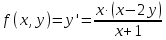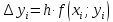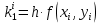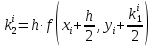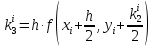Главная страница
Навигация по странице:

  • Задание 71

    		•

    Высшая математика. 2 задания по математике. Решение Заштрихованная область состоит из области D(BC) из которой нужно вырезать два участка принадлежащих D


    Скачать 106.35 Kb.
    НазваниеРешение Заштрихованная область состоит из области D(BC) из которой нужно вырезать два участка принадлежащих D
    АнкорВысшая математика
    Дата01.06.2022
    Размер106.35 Kb.
    Формат файлаdocx
    Имя файла2 задания по математике.docx
    ТипРешение
    #562466

    Задание 21

    В приведённых диаграммах Эйлера-Венна представьте заштрихованные области максимально компактными логическими выражениями, в которых бы использовалось минимальное количество операций и букв.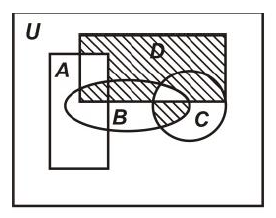


    Решение:

    Заштрихованная область состоит из области D(BC) из которой нужно вырезать два участка принадлежащих D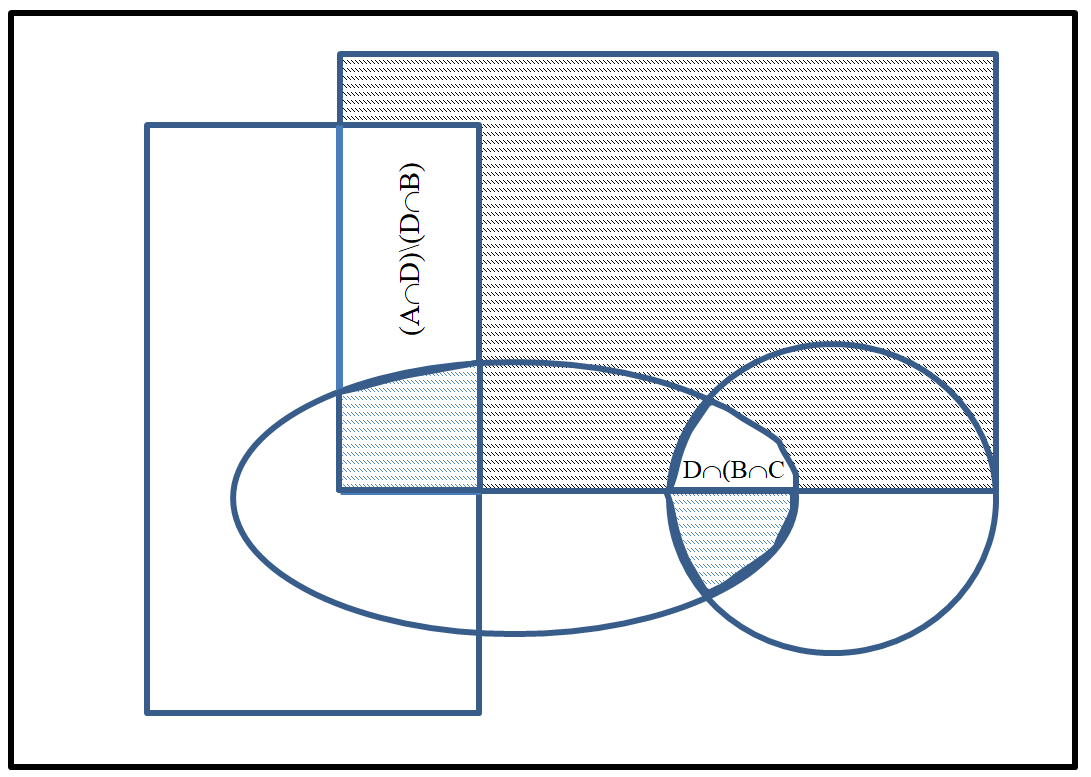

    Чтобы получить необходимое множество необходимо между этими тремя выражениями поставить операцию вычитания. В результате получаем:
    (D((BC))\(D(BC))\((AD)\(DB))


    Задание 71

    Составить на отрезке [𝑚,𝑛] таблицу значений интеграла дифференциального уравнения, удовлетворяющего начальному условию 𝑦(𝑘)=𝑎, выбрав шаг ℎ=0.1: a) методом Эйлера; б) методом Адамса.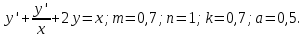


    Решение:
    Представим дифференциальное уравнение в виде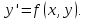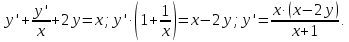





    а) решение методом Эйлера

    Значения yi интеграла дифференциального уравнения могут быть определены по формулам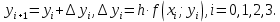



    для вычисления значений составим расчетную таблицу.


    i
    x
    y




    0
    0,7
    0,5000
    -0,1235
    -0,01235

    1
    0,8
    0,4876
    -0,0779
    -0,00779

    2
    0,9
    0,4799
    -0,0283
    -0,00283

    3
    1,0
    0,4770
    0,0230
    0,00230


    б) решение методом Адамса

    Экстраполяционная формула Адамса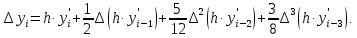



    Значения функции определяют по формуле: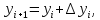



    где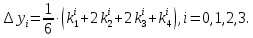

    Для начала процесса используем значения, найденные методом Рунге-Кутта: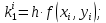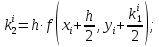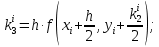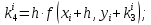









    Из условия задачи имеем 𝑦(0,7) = 0,5:

    i
    xi = x0  ih








    0
    0,7
    -0,01235
    -0,01018
    -0,01028
    -0,01027

    1
    0,8
    -0,00779
    -0,00540
    -0,00511
    -0,00510

    2
    0,9
    -0,00283
    -0,00034
    -0,00046
    -0,00045

    3
    1
    0,00230
    0,00480
    0,00467
    0,00468




    i
    xi = x0  ih
    yi
    yi
    hy'
    hy'
    2hy'
    2hy'

    0
    0,7
    0,5
    -0,01059
    -0,1235
    0.0456
    0,0040
    -0,0023

    1
    0,8
    0,48941
    -0,00585
    -0,0779
    0,0496
    0,0017



    2
    0,9
    0,48356
    -0,00432
    -0,0283
    0,0513






    3
    1
    0,47924



    0,0230










    Метод Адамса заключается в продолжении диагональной таблицы разностей с помощью формулы Адамса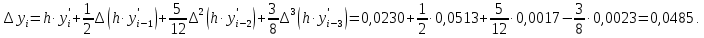

    написать администратору сайта