СИСмод. Решение злп графическим методом

• Название: Решение злп графическим методом
• Анкор: СИСмод
• Дата: 03.03.2023
• Размер: 130.18 Kb.
• Имя файла: LR2_Kurbatov_NA_IVT-323.docx
• Тип: Отчет; #966599

Министерство образования и науки Российской Федерации

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра АСУ


ОТЧЕТ

по лабораторной работе №2

По дисциплине: «Системный анализ и исследование операций»

Тема: ««Решение ЗЛП графическим методом»

Вариант 16
Выполнил:

Ст. гр. ИВТ-323 Курбатов Н.А.

Принял:

Кондратьева О.В.
Уфа 2021 г.

Цель работы: Получить навыки решения ЗЛП графическим методом.

Ход работы:

Питательные вещества	Количество питательных веществ на 1 кг			Норма
	Корма 1 вида	Корма 2 вида
Белки	4	3	12
Углеводы	1	2	12
Протеин	1	5	14
Стоимость 1 кг	5	10

x-количество продукции 1 вида;

y- количество продукции 2 вида;

ЦФ: F(x)=5*x+10*y -> min;

Система ограничений:

{4𝑥 + 3𝑦 ≥ 12

𝑥 + 2𝑦 ≥ 12

𝑥 + 5𝑦 ≥ 14

𝑥 ≥ 0; 𝑦 ≥ 0

Заменим неравенства на равенства и приведем уравнения к виду y=kx+b.

{y1= 4 – 4/3*x

y2= 6 - x/2

y3= 14/5 – x/5

𝑥 ≥ 0; 𝑦 ≥ 0

Построим прямые по 2 точкам и направляющий вектор.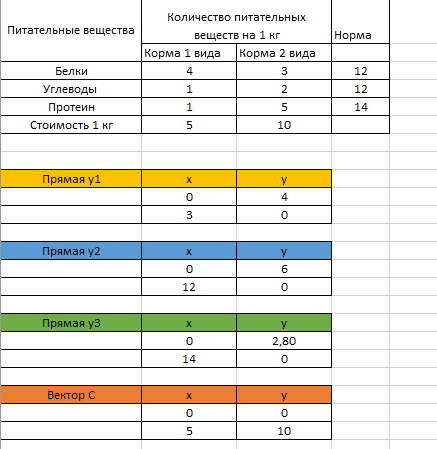



Рисунок 1 – точки прямых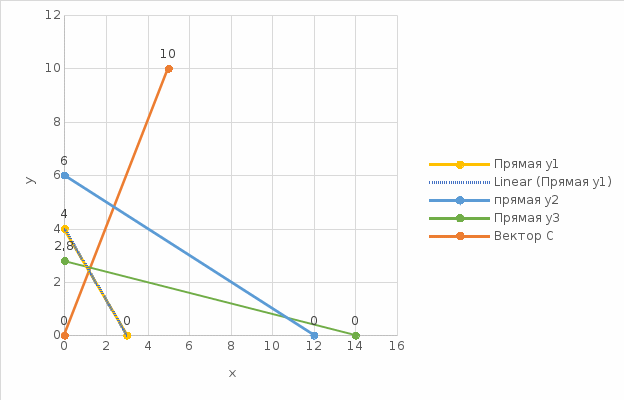



Рисунок 2 – прямые на графике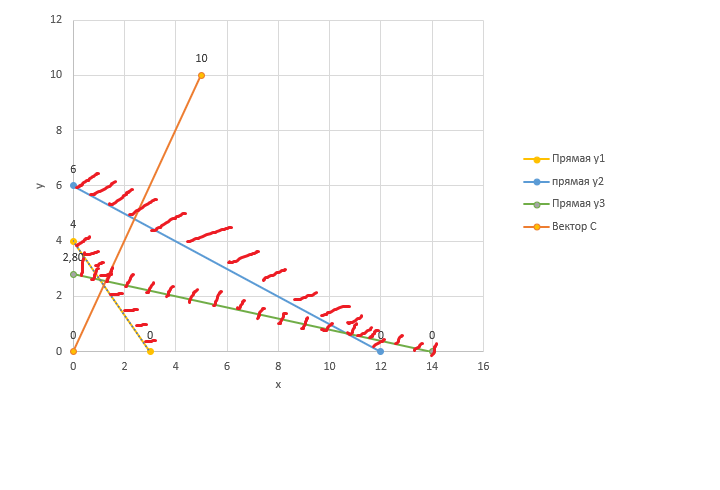



Рисунок 3 – график с одз

Точка оптимума будет находиться на ломанной ABCDE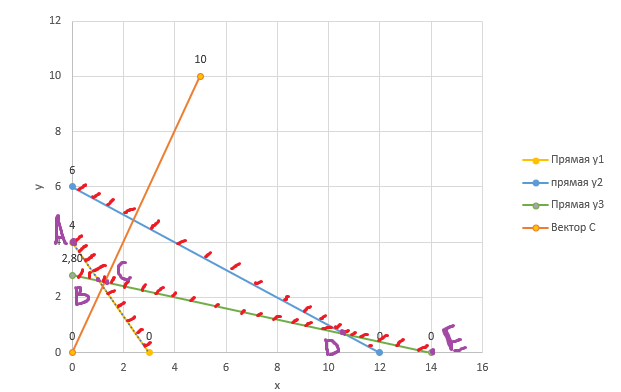



Рисунок 4 – ломанная ABCDE

Построим F(y2) и будем передвигать по оси направляющего вектора в поиске оптимального решения в направлении осей начала координат (минимизация).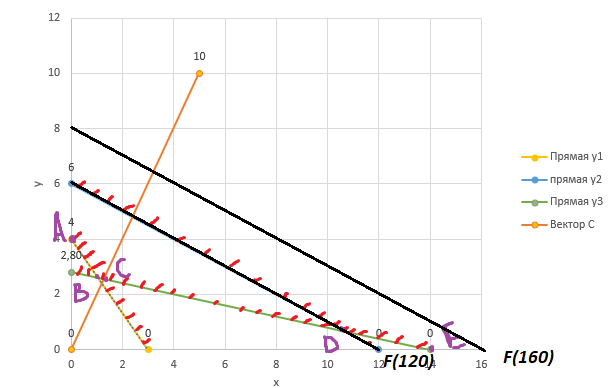



Рисунок 5 – поиск оптимального решения

Прямая перпендикулярная направляющему вектору с координатами (16;8) = 5*x+10*y=5*16+10*8=160; F(160)

(12;6)=5*12+10*6=120; F(120)

Видим, что значение функции уменьшается, ищем оптимальное решение.

Найдем точку С.

Точка С лежит на пересечении прямых y3 и направляющего вектора С решим систему неравенств