хух. Ргр Динамика вращательного движения Условие задачи
 Скачать 73.93 Kb. Скачать 73.93 Kb.
|
|
Ргр: «Динамика вращательного движения» Условие задачи Сплошной цилиндр массой 50 кг и радиусом 0,30 м вращается без начальной скорости вокруг своей оси. На него действуют пара сил с величиной момента М=21 Дж и моментом сопротивления модуль которого является функцией угловой скорости Mсопр.=k·ω2, где k=2,1 кг·м2. Сколько оборотов сделает цилиндр до того, как его угловая скорость станет равной 2 рад/с. Краткое теоретическое содержание Ось вращения тела – прямая, на которой лежат центры окружностей, по которым движутся точки твердого тела при его вращении. Окружности, по которым движутся точки тела, лежат в плоскостях, перпендикулярных к этой оси. Угловая скорость - векторная величина, характеризующая быстроту вращения, ориентацию оси вращения в пространстве и направление вращения. Модуль угловой скорости определяется формулой: Единица угловой скорости [рад/с]. Угловое ускорение – векторная величина, характеризующая изменение угловой скорости со временем. Момент инерции, величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. В механике различают М. и. осевые и центробежные. Осевым М. и. тела относительно оси z называется величина, определяемая равенством: где mi — массы точек тела, hi — их расстояния от оси z, r — массовая плотность, V — объём тела. Величина Iz является мерой инертности тела при его вращении вокруг оси. Пара сил – две равные по модулю и противоположно направленные силы, не действующие вдоль одной прямой. Момент силы – векторная величина, модуль которой равен произведению силы на плечо: 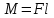 , , 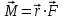 . Если на тело действует 2 момента сил, вызывающих вращение в противоположном направлении, то один из них условно считают положительным, а второй отрицательным. . Если на тело действует 2 момента сил, вызывающих вращение в противоположном направлении, то один из них условно считают положительным, а второй отрицательным.Плечо – кратчайшее расcтояние от оси вращения до линии действия силы. Законы, соотношения, использованные при решении Второй закон Ньютона для вращательного движения: 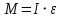 , где М – момент силы, Н•м; I – момент инерции, кг•м2; ε – угловое ускорение, рад/с2. , где М – момент силы, Н•м; I – момент инерции, кг•м2; ε – угловое ускорение, рад/с2.Число оборотов равно: 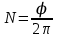 , где N – число оборотов, φ – угол поворота, рад. , где N – число оборотов, φ – угол поворота, рад.Модуль угловой скорости определяется формулой: 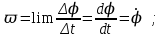 где где 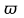 - модуль угловой скорости; - модуль угловой скорости; 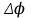 - угол, на который поворачивается тело за промежуток времени - угол, на который поворачивается тело за промежуток времени 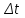 . .Угловое ускорение вычисляется по следующей формуле: 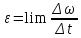 Момент инерции тела: 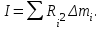 Момент инерции сплошного цилиндра: 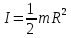 . .Модуль момента силы равен: 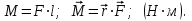 где l – плечо. где l – плечо.Пояснение ко всем величинам, входящим в формулы и соотношения: 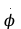 - первая производная угла по времени; [ - первая производная угла по времени; [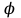 ]- рад. ]- рад. - модуль углового ускорения; [ - модуль углового ускорения; [ ]-рад/с ]-рад/с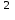 . .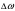 - изменение угловой скорости за время - изменение угловой скорости за время 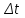 ; [ ; [ ] - рад/с. ] - рад/с.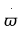 - первая производная угловой скорости по времени; [ - первая производная угловой скорости по времени; [ ] - рад/с. ] - рад/с.I - момент инерции тела; [I] - 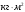 . .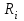 - расстояние от оси до элементарной массы; - расстояние от оси до элементарной массы;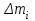 - элементарная масса; - элементарная масса;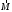 - момент силы; [ - момент силы; [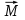 ] = Н*м. ] = Н*м.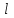 - плечо; [ - плечо; [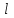 ] – м. ] – м.F– сила, действующая на тело; [F] = Н. N – число оборотов, совершаемое телом. Г 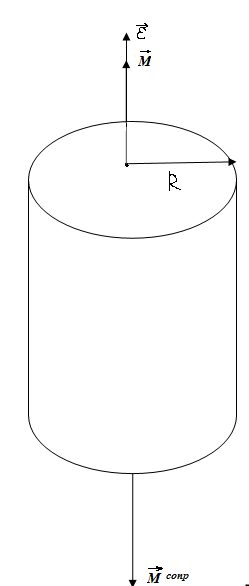 рафический материал Решение. В основе данной расчетно-графической работы лежит вращательное движение цилиндра относительно неподвижной оси, которая проходит через центр тяжести. По закону вращательного движения 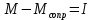 (1) (1)где  - угловое ускорение, а I - момент инерции тела. - угловое ускорение, а I - момент инерции тела.По определению угловое ускорение равно: 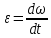 , ,где ω - угловая скорость. По условию Мсопр = k•ω2. Формулу (1) перепишем в виде: 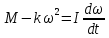 Воспользуемся соотношением 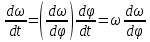 И подставим его в уравнение: 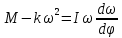 Разделим переменные в получившемся дифференциальном уравнении и проинтегрируем: 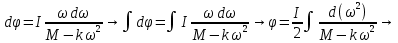 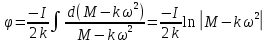 Число оборотов равно: 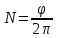 Подставляем: 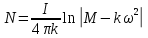 Момент инерции для цилиндра относительно оси OO1 согласно теореме Штейнера равна: 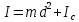 = =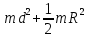 В данном случае ось проходит через образующую цилиндра, следовательно d = R, где R – радиус цилиндра. Окончательно имеем: 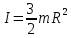 Следовательно: 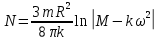 Подставим в формулу числовые значения и вычислим: 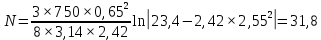 об. об.График зависимости момента силы от времени Момент силы остается равным 23,4 Дж на протяжении всего времени наблюдения. 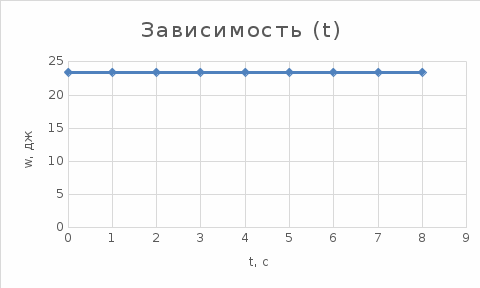 График зависимости угловой скорости от времени. Выразив угловое ускорение из основного уравнения динамики вращательного движения мы получим : 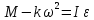 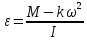 = = 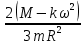 подставим ω=1рад/c и найдем угловое ускорение 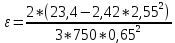 = 0,02 = 0,02Уравнение равноускоренного движения: 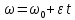 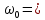 0 так как вращение происходит без начальной скорости. Найдем t конечное, подставив в формулу значение угловой скорости из условия. 0 так как вращение происходит без начальной скорости. Найдем t конечное, подставив в формулу значение угловой скорости из условия.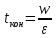 = = 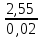 = 127,5 с = 127,5 сЗная, что 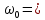 0 , мы можем построить график: 0 , мы можем построить график:Отсюда, угловое ускорение можно выразить следующим образом Вывод: Сплошной цилиндр, массой 750 кг вращающийся без начальной скорости, сделает 31,8 оборота до того, как его угловая скорость станет равной 2,55 рад/с. |
