Относительный риск и отношение шансов. Риск в эпидемиологии вероятностная мера возникновения неблагоприятного события или явления, (заболевание, смерть, возникновение эпидемии). Риск непосредственный
 Скачать 256.6 Kb. Скачать 256.6 Kb.
|
|
Риск (непосредственный, относительный) Риск - в эпидемиологии вероятностная мера возникновения неблагоприятного события или явления, (заболевание, смерть, возникновение эпидемии). Риск непосредственный - показатель, отражающий разницу заболеваемости в коллективах, подвергавшихся и не подвергавшихся действию фактора риска, но равноценных по всем другим признакам. Риск относительный - показатель, коэффициент, отражающий соотношение числа заболевших, среди относящихся к группе риска к заболевшим, не относящимся к ней, т. е. Р.отн.=(риск у подвергшихся воздействию)/(риск у не подвергшихся воздействию) Данный показатель отражает индивидуальный относительный риск и применяется при исследованиях когортных, когда регистрируется либо не регистрируется заболевание, а затем возникает необходимость наблюдать заболевших. Показатель используется с целью оценки степени вероятности того, что воздействие фактора с результатом воздействия находятся в причинной связи. ОТНОСИТЕЛЬНЫЙ РИСК Риск - это вероятность появления определенного исхода, например, болезни или травмы. Риск может принимать значения от 0 (вероятность наступления исхода отсутствует) до 1 (во всех случаях ожидается неблагоприятный исход). В медицинской статистике, как правило, изучаются изменения риска наступления исхода в зависимости от какого-либо фактора. Пациенты условно разделяются на 2 группы, на одну из которых фактор влияет, на другую – нет. Относительный риск - это отношение частоты исходов среди исследуемых, на которых оказывал влияние изучаемый фактор, к частоте исходов среди исследуемых, не подвергавшихся влиянию этого фактора. В научной литературе часто используют сокращенное название показателя - ОР или RR (от англ. "relative risk"). 1. История разработки показателя относительного риска Расчет относительного риска заимствован медицинской статистикой из экономики. Правильная оценка влияния политических, экономических и социальных факторов на востребованность товара или услуги может привести к успеху, а недооценка этих факторов - к финансовым неудачам и банкротству предприятия. 2. Для чего используется относительный риск? Относительный риск используется для сравнения вероятности исхода в зависимости от наличия фактора риска. Например, при оценке влияния курения на частоту гипертонической болезни, при изучении зависимости частоты рака молочной железы от приема оральных контрацептивов и др. Относительный риск - важнейший показатель в назначении определенных методов лечения или проведении исследований с возможными побочными эффектами. 3. Условия и ограничения применения относительного риска Показатели фактора и исхода должны быть измерены в номинальной шкале (например, пол пациента - мужской или женский, артериальная гипертония - есть или нет). Данный метод позволяет проводить анализ только четырехпольных таблиц, когда и фактор, и исход являются бинарными переменными, то есть имеют только два возможных значения (например, возраст младше или старше 50 лет, наличие или отсутствие определенного заболевания в анамнезе). Относительный риск применяется при проспективных исследованиях, когда исследуемые группы формируются по признаку наличия или отсутствия фактора риска. При исследованиях по принципу "случай-контроль" вместо относительного риска должен использоваться показатель отношения шансов. 4. Как рассчитать относительный риск? Для расчета относительного риска необходимо: Строим четырехпольную таблицу сопряженности, исходя из количества исследуемых, имеющих определенные значения факторного и результативного признаков:
Находим значение относительного риска по следующей формуле: 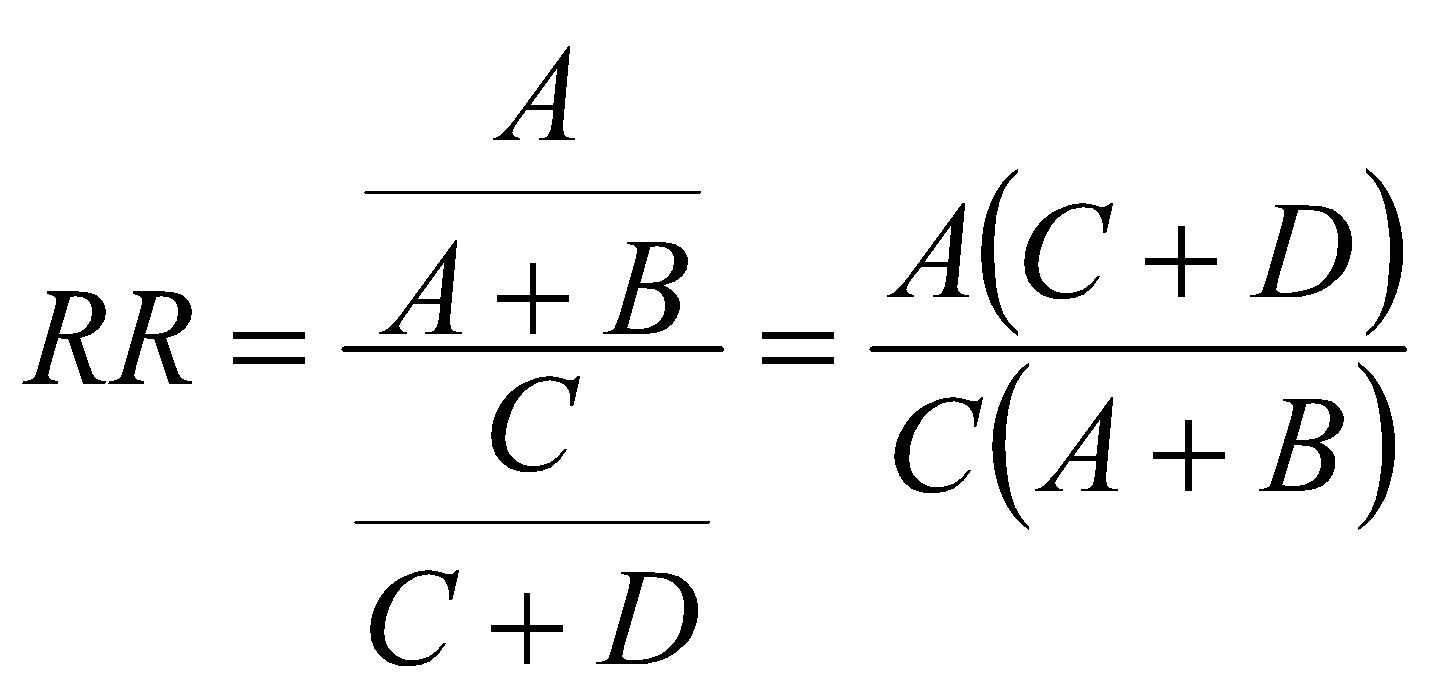 где A, B, C, D – количество наблюдений в ячейках таблицы сопряженности. Находим значения границ доверительного интервала - 95% ДИ (или 95% CI - от англ. "confidence interval"). Формула расчета верхней границы: Формула расчета нижней границы доверительного интервала: Сравниваем значения относительного риска и границ доверительного интервала с единицей. Гипотезы для равенства пропорций, выраженные в относительном риске 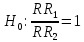 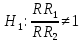 5. Как интерпретировать значение относительного риска? Показатель относительного риска сравнивается с 1 для того, чтобы определить характер связи фактора и исхода: Если ОР равен 1, можно сделать вывод, что исследуемый фактор не влияет на вероятность исхода (отсутствие связи между фактором и исходом). При значениях более 1 делается вывод о том, что фактор повышает частоту исходов (прямая связь). При значениях менее 1 - о снижении вероятности исхода при воздействии фактора (обратная связь). Также обязательно оцениваются значения границ 95% доверительного интервала. Если оба значения - и нижней, и верхней границы - находятся по одну сторону от 1, или, другими словами, доверительный интервал не включает 1, то делается вывод о статистической значимости выявленной связи между фактором и исходом с вероятностью ошибки p<0,05. Если нижняя граница 95% ДИ меньше 1, а верхняя - больше, то делается вывод об отсутствии статистической значимости влияния фактора на частоту исхода, независимо от величины показателя ОР (p>0,05). 6. Пример расчета показателя относительного риска В 1999 году в Оклахоме проводились исследования заболеваемости мужчин язвой желудка. В качестве влияющего фактора было выбрано регулярное потребление фастфуда. В первой группе находились 500 мужчин, постоянно питающихся быстрой пищей, среди которых язву желудка диагностировали у 96 человек. Во вторую группу были отобраны 500 сторонников здорового питания, среди которых язва желудка была диагностирована в 31 случае. Исходя из полученных данных была построена следующая таблица сопряженности:
Рассчитываем значение относительного риска: Находим значения верхней и нижней границ 95% доверительного интервала по формулам. Формула расчета верхней границы: Формула расчета нижней границы доверительного интервала: Сравниваем полученные значения RR и 95% ДИ с 1. Показатель относительного риска свидетельствует о наличии прямой связи между употреблением фастфуда и вероятностью развития язвы желудка. У мужчин, употребляющих картошку фри и хотдоги, риск возникновения язвы желудка в 3,1 раза выше, чем среди мужчин придерживающихся здорового питания. Уровень значимости данной взаимосвязи соответствует p<0.05, так как 95% ДИ=(2,11; 4,55) не включает в себя единицу. 7. Разность рисков Разность рисков (атрибутивный риск) – разность пропорций – выборочная (оценочная) разность рисков 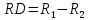 где 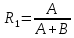 , , 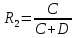 , ,95% доверительный интервал для RD: 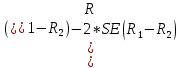 ; ; 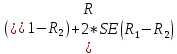 ) )где 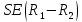 - стандартная ошибка разности двух выборочных пропорций - стандартная ошибка разности двух выборочных пропорций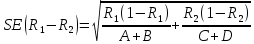 Пример: разность риска ВИЧ-инфекции для детей, рожденных от ВИЧ-положительных матерей, которые принимали AZT, по сравнению с теми, кто не принимал. Используем данные клинического испытания антиретровирусного лечения как средства профилактики передачи ВИЧ-инфекции от матери к ребенку. Дизайн исследования – «рандомизированное двойное-слепое плацебо-контролируемое испытание эффективности и безопасности зидовудина (AZT) в снижении риска вертикальной передачи ВИЧ-инфекции (от матери к ребенку)» – 363 ВИЧ-инфицированные беременные женщины были случайным образом распределены в экспериментальную (AZT) или контрольную (плацебо) группу. Результаты: 1) среди 180 женщин в группе AZT 13 женщин родили детей, которые имели положительный результат теста на ВИЧ-инфекцию в течение 18 месяцев после рождения 2) среди 183 женщин в контрольной (плацебо) группе AZT 40 женщин родили детей, которые имели положительный результат теста на ВИЧ-инфекцию в течение 18 месяцев после рождения. • Случайное распределение воздействия (лечения) – Способствует тому, что две группы могут быть сравнимыми – Пациент и врач не могут влиять на получение определенного лечения. • Двойное-слепое – Ни пациент, ни врач не знают, какое лечение предоставляется. (Источник: *Conner, E., et al. (1994). Reduction of maternal-infant transmission of human immunodeficiency virus type 1 with zidovudine treatment, New England Journal of Medicine 331: 18.) • AZT 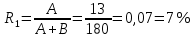 , ,• Плацебо 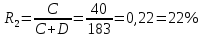 , ,Тогда разность рисков будет равна 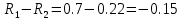 Интерпретация, оценка выборки – Если AZT будут принимать 1000 ВИЧ-инфицированных беременных женщин, это позволит сократить число инфицирования рожденных детей ВИЧ-инфекцией на 150 случаев (по сравнению к числу ВИЧ инфицированных детей, рожденных от 1000 женщин, не принимавших AZT). 95% доверительный интервал: исследование AZT Поскольку, 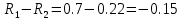 , то 95%ДИ будет: , то 95%ДИ будет:(-0,15-2*0,036; -0,15+2*0,036)=(-0,222; -0,078) где 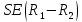 - стандартная ошибка разности двух выборочных пропорций - стандартная ошибка разности двух выборочных пропорций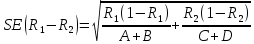 = =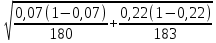 =0,036 =0,036Интерпретация 95% ДИ – Результаты исследования предполагают, что снижение числа случаев ВИЧ-инфекции среди детей, родившихся от 1000 ВИЧ-инфицированных беременных женщин, получавших AZT, может варьировать от 75 до 220 по сравнению с числом случаев среди детей, рожденных от 1000 женщин, не получавших AZT. Абсолютное уменьшение пропорции ВИЧ-инфицированных детей, рожденных от ВИЧ- положительных матерей, ассоциированное с приемом AZT, оценивается от 7,8% до 22,2%. ОТНОШЕНИЕ ШАНСОВ Отношение шансов – статистический показатель (на русском его название принято сокращать как ОШ, а на английском - OR от "odds ratio"), один из основных способов описать в численном выражении то, насколько отсутствие или наличие определённого исхода связано с присутствием или отсутствием определённого фактора в конкретной статистической группе. 1. История разработки показателя отношения шансов Термин "шанс" пришел из теории азартных игр, где при помощи данного понятия обозначали отношение выигрышных позиций к проигрышным. В научной медицинской литературе показатель отношения шансов был впервые упомянут в 1951 году в работе Дж. Корнфилда. Впоследствии данным исследователем были опубликованы работы, в которых отмечалась необходимость расчета 95% доверительного интервала для отношения шансов. (Cornfield, J. A Method for Estimating Comparative Rates from Clinical Data. Applications to Cancer of the Lung, Breast, and Cervix // Journal of the National Cancer Institute, 1951. - N.11. - P.1269–1275.) 2. Для чего используется показатель отношения шансов? Отношение шансов позволяет оценить связь между определенным исходом и фактором риска. Отношение шансов позволяет сравнить группы исследуемых по частоте выявления определенного фактора риска. Важно, что результатом применения отношения шансов является не только определение статистической значимости связи между фактором и исходом, но и ее количественная оценка. 3. Условия и ограничения применения отношения шансов Результативные и факторные показатели должны быть измерены в номинальной шкале. Например, результативный признак - наличие или отсутствие врожденного порока развития у плода, изучаемый фактор - курение матери (курит или не курит). Данный метод позволяет проводить анализ только четырехпольных таблиц, когда и фактор, и исход являются бинарными переменными, то есть имеют только два возможных значения (например, пол - мужской или женский, артериальная гипертония - наличие или отсутствие, исход заболевания - с улучшением или без улучшения). Сопоставляемые группы должны быть независимыми, то есть показатель отношения шансов не подходит для сравнения наблюдений "до"-"после". Показатель отношения шансов используется в исследованиях по типу "случай-контроль" (например, первая группа - больные гипертонической болезнью, вторая - относительно здоровые люди). Для проспективных исследований, когда группы формируются по признаку наличия или отсутствия фактора риска (например, первая группа - курящие, вторая группа - некурящие), обычно рассчитывается относительный риск. 4. Как рассчитать отношение шансов? Отношение шансов - это значение дроби, в числителе которой, находятся шансы определённого события для первой группы, а в знаменателе шансы того же события для второй группы. Шансом является отношение числа исследуемых, имеющих определенный признак (исход или фактор), к числу исследуемых, у которых данный признак отсутствует. Гипотезы для равенства пропорций, выраженные в отношении шансов 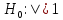 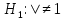 Например, была отобрана группа пациентов, прооперированных по поводу панкреонекроза, число которых составило 100 человек. Через 5 лет из их числа в живых осталось 80 человек. Соответственно, шанс выжить составил 80 к 20, или 4,0. Удобным способом является расчёт отношения шансов со сведением данных в таблицу 2х2:
Для данной таблицы отношение шансов рассчитывается по следующей формуле: OR= 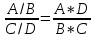 Очень важно оценить статистическую значимость выявленной связи между исходом и фактором риска. Связано это с тем, что даже при невысоких значениях отношения шансов, близких к единице, связь, тем не менее, может оказаться существенной и должна учитываться в статистических выводах. И, наоборот, при больших значениях OR, показатель оказывается статистически незначимым, и, следовательно, выявленной связью можно пренебречь. Для оценки значимости отношения шансов рассчитываются границы 95% доверительного интервала (используется аббревиатура 95% ДИ или 95% CI от англ. "confidence interval"). Формула для нахождения значения верхней границы 95% CI: Формула для нахождения значения нижней границы 95% CI: 5. Как интерпретировать значение отношения шансов? Если отношение шансов превышает 1, то это означает, что шансы обнаружить фактор риска больше в группе с наличием исхода. Т.е. фактор имеет прямую связь с вероятностью наступления исхода. Отношение шансов, имеющее значение меньше 1, свидетельствует о том, что шансы обнаружить фактор риска больше во второй группе. Т.е. фактор имеет обратную связь с вероятностью наступления исхода. При отношении шансов, равном единице, шансы обнаружить фактор риска в сравниваемых группах одинакова. Соответственно, фактор не оказывает никакого воздействия на вероятность исхода. Дополнительно в каждом случае обязательно оценивается статистическая значимость отношения шансов исходя из значений 95% доверительного интервала. Если доверительный интервал не включает 1, т.е. оба значения границ или выше, или ниже 1, делается вывод о статистической значимости выявленной связи между фактором и исходом при уровне значимости p<0,05. Если доверительный интервал включает 1, т.е. его верхняя граница больше 1, а нижняя - меньше 1, делается вывод об отсутствии статистической значимости связи между фактором и исходом при уровне значимости p>0,05. Величина доверительного интервала обратно пропорциональна уровню значимости связи фактора и исхода, т.е. чем меньше 95% ДИ, тем более существенной является выявленная зависимость. 6. Пример расчета показателя отношения шансов Представим две группы: первая состояла из 200 женщин, у которых был диагностирован врожденный порок развития плода (Исход+). Из них курили во время беременности (Фактор+) - 50 человек (А), являлись некурящими (Фактор-) - 150 человек (С). Вторую группу составили 100 женщин без признаков ВПР плода (Исход -) среди которых курили во время беременности (Фактор+) 10 человек (B), не курили (Фактор-) - 90 человек (D). 1. Составим четырехпольную таблицу сопряженности:
2. Рассчитаем значение отношения шансов: OR=(A*D)/(B*C)=(50*90)/(150*10)=3. 3. Найдем границы 95% CI. Формула для нахождения значения верхней границы 95% CI: Формула для нахождения значения нижней границы 95% CI: Значение нижней границы, рассчитанной по указанной выше формуле составило 1,45, а верхней - 6,21. Таким образом, исследование показало, что шансы встретить курящую женщину среди пациенток с диагностированным ВПР плода в 3 раза выше, чем среди женщин без признаков ВПР плода. Наблюдаемая зависимость является статистически значимой, так как 95% CI не включает 1, значения его нижней и верхней границ больше 1. |
