Приложение. Приложение А. Рисунок 1 Структурная схема установки
 Скачать 215.99 Kb. Скачать 215.99 Kb.
|
|
Приложение А. Проверка основных результатов работы посредством схемотехнического моделирования Для проверки основных результатов расчетов, выполненных в курсовой работе, проведем имитационное моделирование подлежащего дискретизации сигнала, непосредственно самой процедуры дискретизации и последующего восстановления сигнала заданным фильтром. Для этого воспользуемся симулятором Electronic Workbench и методическими указаниями [2]. Структурная схема установки представлена на рисунке 1. 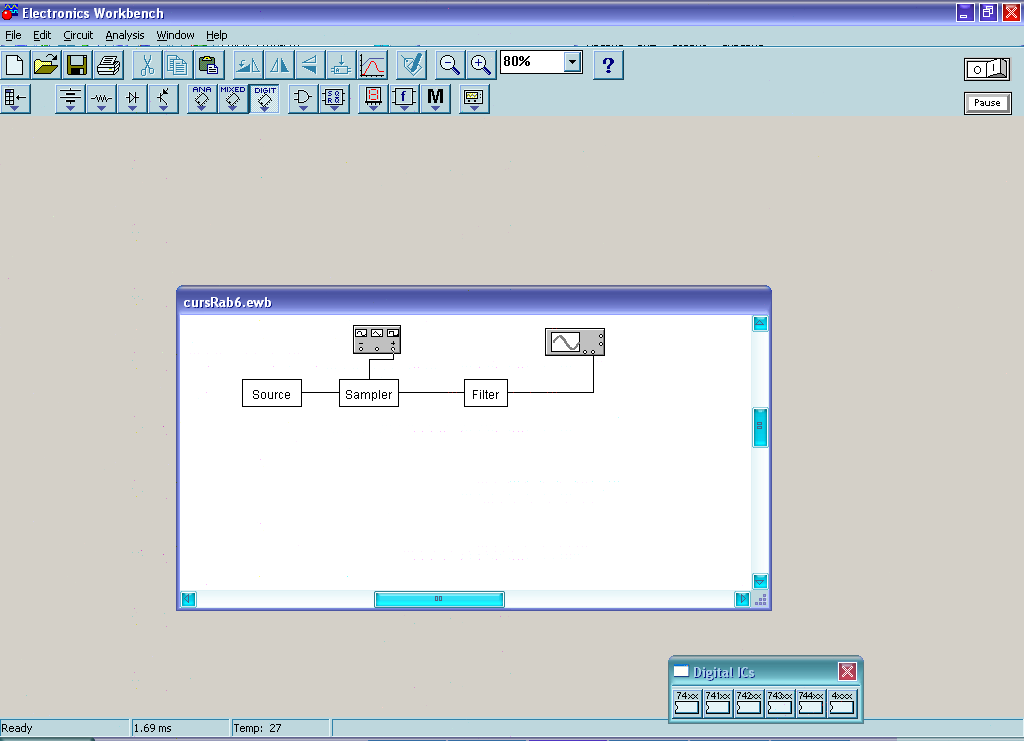 Рисунок 1 - Структурная схема установки Будем выполнять моделирование поэтапно. 1 Моделирование сигнала подлежащего дискретизации (блок Source) Поскольку заданный сигнал (рисунок 1 в расчетно-пояснительной записке - РПЗ) представлен двумя разными по характеру функциями – сложной на интервале времени от нуля до половины длительности импульса, и полиномиальной - на оставшемся интервале, то его моделирование выполним методами функционального нелинейного преобразования стандартных сигналов (для сложной функции) и интегрирования и коммутаций сигнала включения (для полиномиальной части). На рисунке 2 изображена полученная схема, на рисунке 3 – смоделированный сигнал. 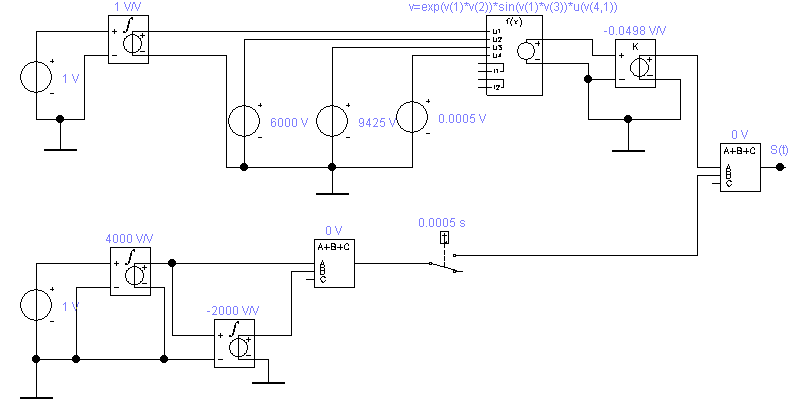 Рисунок 2 – блок Source, моделирующий исходный сигнал 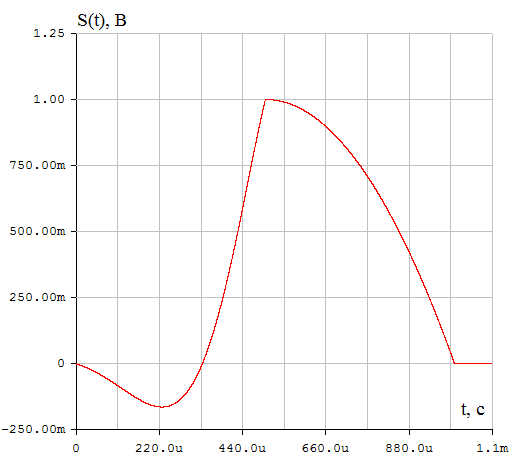 Рисунок 3 – исходный непрерывный сигнал Сопоставляя рисунок 3 с рисунком 1 (РПЗ), приходим к выводу, что эти сигналы совпадают. С помощью команды "Fourier Analysis…" построим спектральную плотность амплитуд исходного сигнала (рисунок 4). 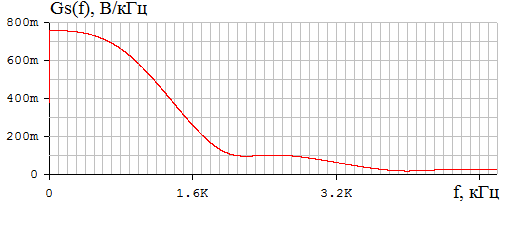 Рисунок 4 - спектральная плотность амплитуд исходного непрерывного сигнала Поскольку анализ спектральных характеристик в программе Electronic Workbench ориентирован преимущественно на исследование периодических сигналов, то при сопоставлении спектральных плотностей, моделированной и рассчитанной теоретически (рисунок 4 в РПЗ), будем получать отличие их масштабов в два раза. В симуляторе спектральная плотность амплитуд строится на основе амплитудного спектра, который всегда вдвое больше комплексного. Следует заметить, что данное отличие не играет важной роли, так как изменение масштаба не есть искажение. Таким образом, первый этап моделирования завершен – схема, реализующая заданный сигнал собрана. 2 Моделирование процедуры дискретизации Дискретизированный сигнал можно реализовать путем стробирования исходного непрерывного сигнала периодической последовательность малых по длительности импульсов, повторяющихся с частотой дискретизации. Тогда получим схему, представленную на рисунке 5. 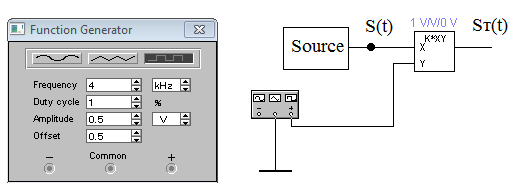 Рисунок 5 – Схема дискретизатора На рисунках 6 и 7 изображены соответственно временные диаграммы исходного и дискретизированного сигналов и спектральная плотность амплитуд дискретизированного сигнала. 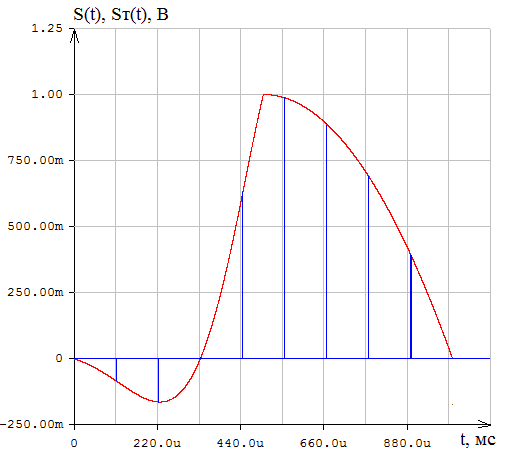 Рисунок 6 - временные диаграммы исходного и дискретизированного сигналов 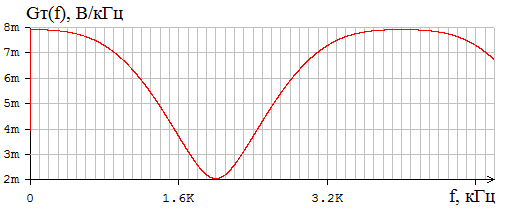 Рисунок 7 - спектральная плотность амплитуд дискретизированного сигнала Таким образом, анализируя рисунки 6 и 7, приходим к выводу, что моделирование совпадает с расчетом. Второй этап завершен. 3 Имитация процесса восстановления непрерывного сигнала по его дискретным отсчетам Процесс восстановления сигнала обеспечивается путем его фильтрации фильтром нижних частот. Смоделируем ФНЧ по заданной передаточной функции фильтра, определяемой выражением 1. 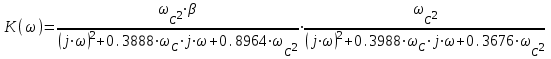 (1) (1)Для этого можно использовать два звена Transfer Function Block. Значения коэффициентов первого и второго звеньев приведены ниже. А01= 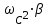 А01= А01=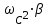 B01= 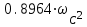 B01= B01=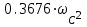 (2) (2)B11= 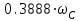 B11= B11=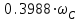 B21=1 B21= 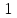 На рисунке 8 приведена структурная схема фильтра, на рисунке 9 – его АЧХ. 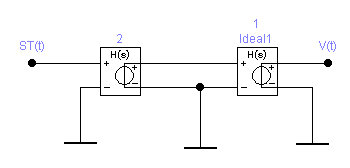 Рисунок 8 – схема восстанавливающего фильтра 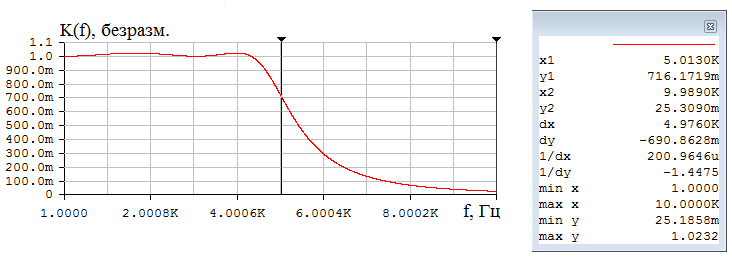 Рисунок 9 – АЧХ восстанавливающего фильтра Рисунок 9 – АЧХ восстанавливающего фильтраПолученная АЧХ совпадает с рассчитанной теоретически. Это подтверждает правильность исследований. Таким образ, полная виртуальная лабораторная установка смоделирована и изображена на рисунке 10. 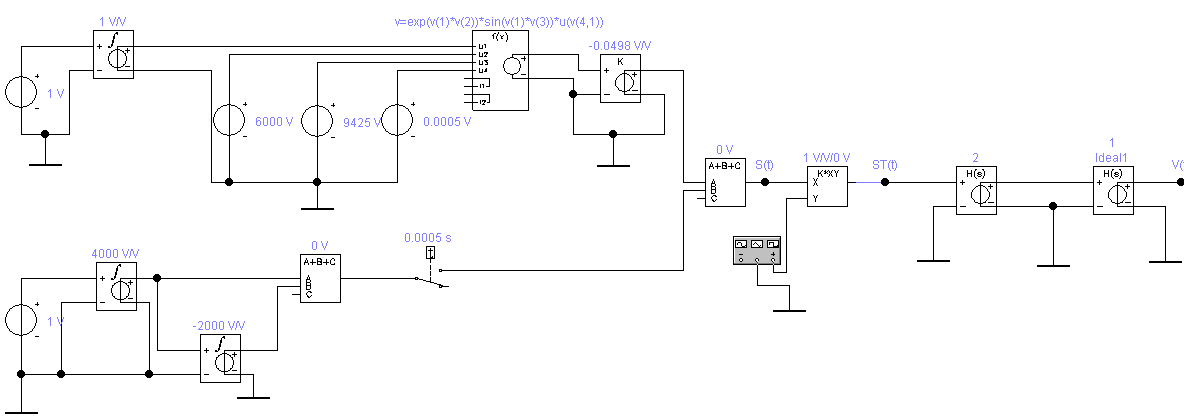 Рисунок 10 – виртуальная лабораторная установка С помощью собранной установки проверим теоретические расчеты восстановленного сигнала, пронаблюдав сигнал на выходе фильтра. Временные диаграммы восстановленного и исходного сигналов изображена на рисунке 11. 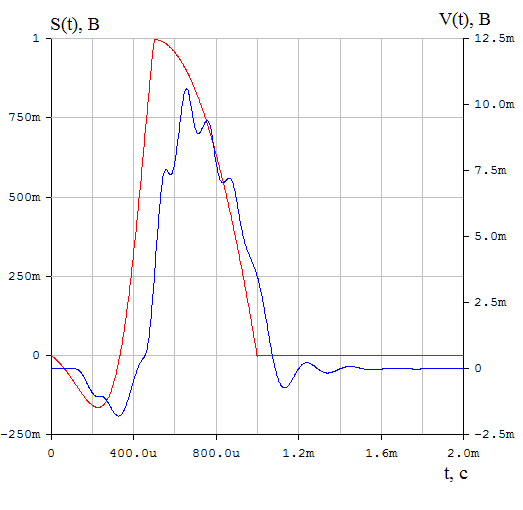 Рисунок 11 - Временные диаграммы восстановленного и исходного сигналов Если сравнивать рисунки 11 и 23(РПЗ), то различия в формах восстановленных сигналов не наблюдаются. Таким образом, моделирование подтверждает правильность расчетов. Данная установка позволяет также исследовать погрешность восстановления при изменении частоты дискретизации. Для этого сначала увеличим в два раза, а затем уменьшив в такое же количество раз, частоту дискретизации и пронаблюдаем осциллограммы входного и выходного сигналов. Результаты изображены на рисунках 12 и13. 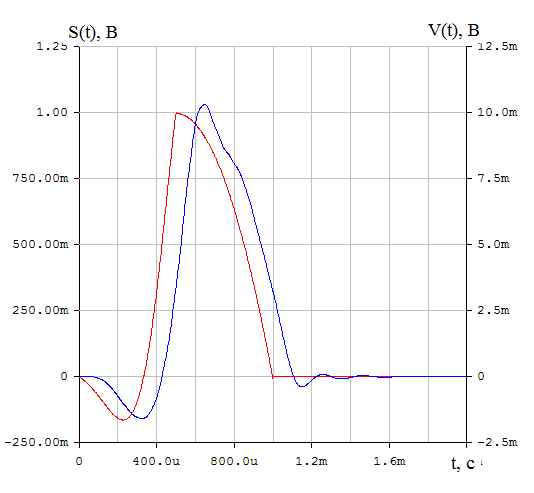 Рисунок 12 – осциллограммы входного и выходного сигналов при увеличенной вдвое частоте дискретизации 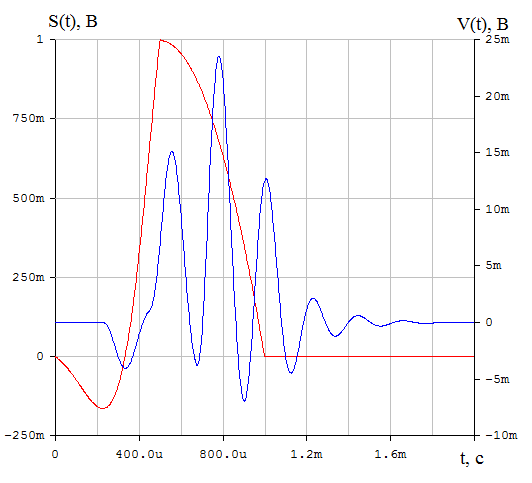 Рисунок 13 – осциллограммы входного и выходного сигналов при уменьшенной вдвое частоте дискретизации Как видно из рисунков, качество восстановления сигнала улучшается при увеличении частоты дискретизации. К такому же выводу пришли ранее, при расчетах. Проверим предположение теории, что при увеличении длительности отсчетных импульсов качество восстановления сигнала должно ухудшиться. Для этого в модели Function Generator коэффициент заполнения периода, увеличив его до двадцати процентов. Посмотрем осциллограммы напряжений на выходах трех блоков. Полученные временные диаграммы изображены на рисунке 14. 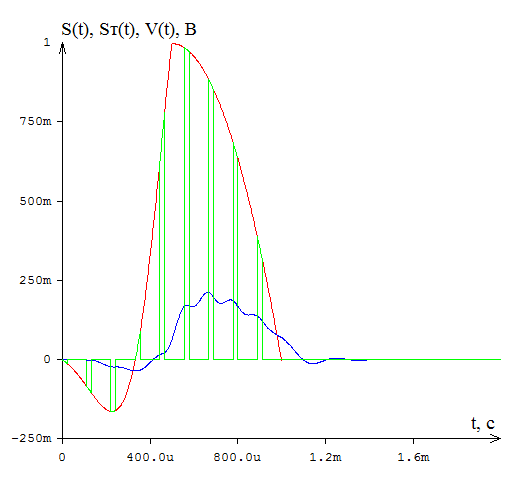 Рисунок 14 – временные диаграммы исходного, дискретизированного и восстановленного сигналов Таким образом, глядя на рисунок 14, можно заключить, что предположение теории подтвердилось – качество восстановления сигнала ухудшилось. |
