маи. БорзенковаМА_ИСТ2018_ПЗ3. Российский государственный социальный университет Факультет информационных технологий практическое задание 3 по дисциплине Математика
 Скачать 2.02 Mb. Скачать 2.02 Mb.
|
ПРАКТИЧЕСКОЕ ЗАДАНИЕ 3 по дисциплине «Математика» Вариант 5
Москва 2019 Задача 1 2. В контрольной точке на морской акватории из придонного слоя отобрали 8 проб воды и определили в них содержание растворенного кислорода, получив следующие значения (мл/л): 5 4 6 2 5 3 4 3 Найти оценку математического ожидания и несмещенную оценку дисперсии. 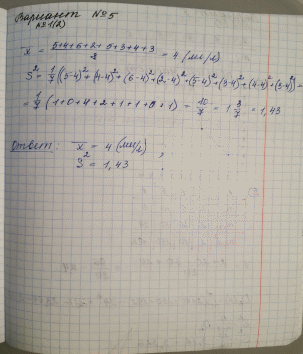 Задача 2 По данному распределению выборки из нормальной совокупности xi 1 4 5 8 mi 2 5 10 3 а) построить полигон относительных частот; б) рассчитать x и 2 s ; в) построить доверительный интервал для M(X) с надежностью 0.95 . 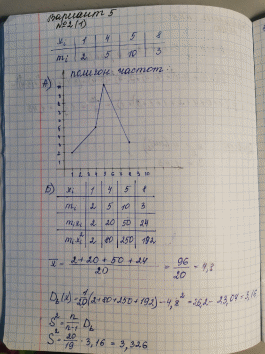 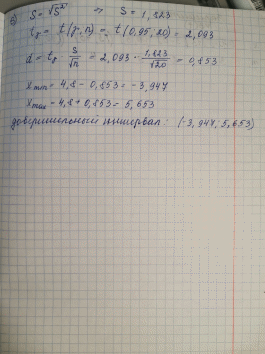 Задача 3 8. В результате эксперимента получены следующие 25 значений 12 13 5 9 -7 7 3 15 1 3 13 1 -10 14 7 -3 2 3 -9 11 4 11 13 4 -3 а) составить интервальный статистический ряд, разбив отрезок [-10; 15] на 5 промежутков равной длины; б) построить гистограмму относительных частот; в) перейти к статистическому ряду, заменив интервалы их серединами, и вычислить x и 2 s ; г) построить доверительный интервал для M(X) с надежностью 0.95 . 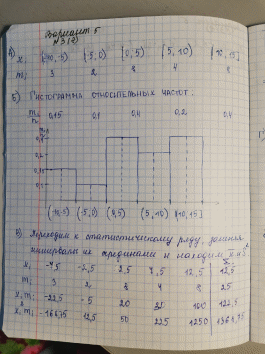 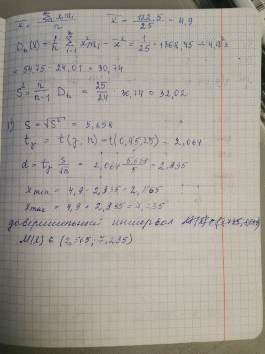 Дополнительное задание 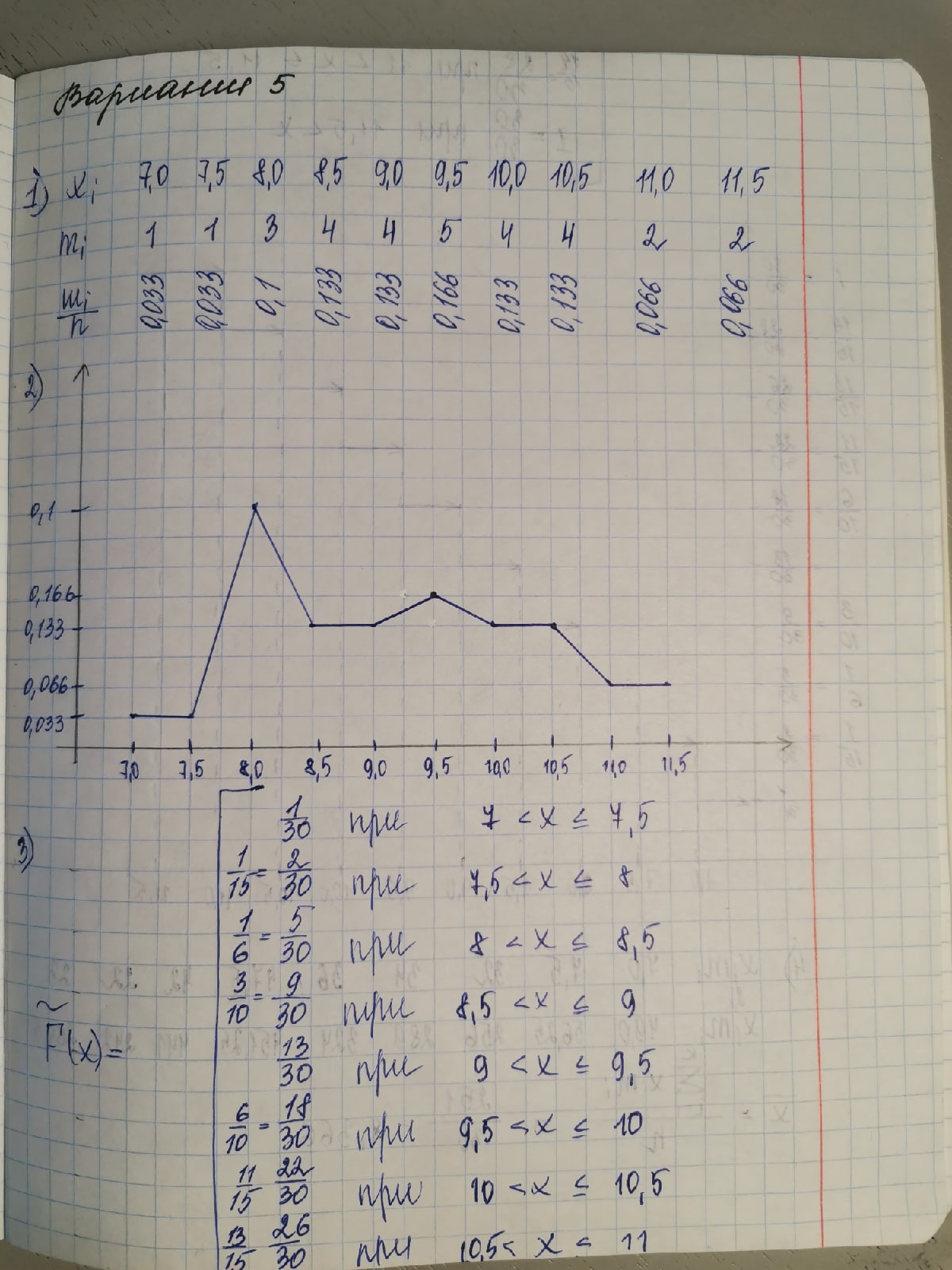 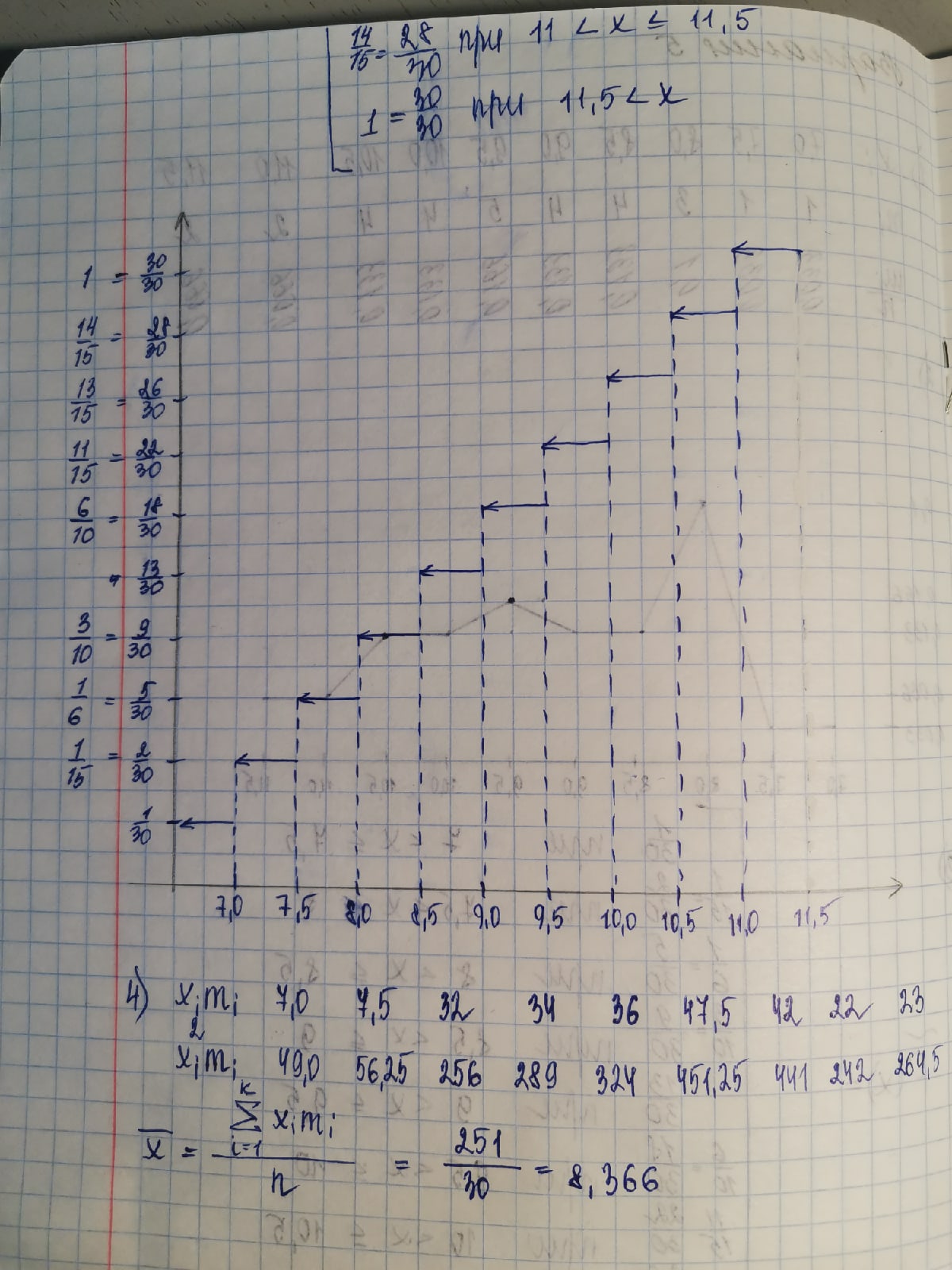  |

