ать определение показателю адиабаты γ. Как его можно рассчитать через степени свободы молекул газа. ЗР-1_Физика_. Российский государственный социальный университет задание к разделу 1 по дисциплине Физика

• Название: Российский государственный социальный университет задание к разделу 1 по дисциплине Физика
• Анкор: ать определение показателю адиабаты γ. Как его можно рассчитать через степени свободы молекул газа
• Дата: 11.01.2022
• Размер: 55.22 Kb.
• Имя файла: ЗР-1_Физика_.docx
• Тип: Документы; #327913

Российский государственный социальный университет

ЗАДАНИЕ К РАЗДЕЛУ 1

по дисциплине «Физика»
Дать определение показателю адиабаты γ.
Как его можно рассчитать через степени свободы молекул газа?
(тема задания к разделу 1)
Вариант: 11

ФИО студента	Демидов Владимир Сергеевич
Направление подготовки	Программная-инженерия
Группа	ПИН-Б-0-Д-2020-1

Москва 2021

Оглавление

Введение 3

Основная часть 4

Заключение 9

Список использованной литературы 10

Введение

Показатель адиабаты (иногда называемый коэффициентом Пуассона) — отношение теплоёмкости при постоянном давлении (Ср) к теплоёмкости при постоянном объёме (Сv). Иногда его ещё называют фактором изоэнтропийного расширения. Обозначается греческой буквой γ (гамма) или k (каппа). Буквенный символ в основном используется в химических инженерных дисциплинах. В теплотехнике используется латинская буква К. Переходя к адиабатическому процессу Cv – это процесс, протекающий в термодинамической системе без теплообмена с окружающей средой. Термодинамической системой является система, содержащая огромное количество частиц. Например, газ, число молекул которого сравнимо с числом Авогадро 6,02∙10²³ 1/моль. Хотя движение каждой частицы подчиняется законам Ньютона, но их так много, что решить систему уравнения динамики для определения параметров системы невозможно. Поэтому состояние системы характеризуют термодинамическими параметрами, такими как давление P, объем V, температура T.

Основная часть

Согласно первому началу термодинамики, являющемуся законом сохранения энергии в термодинамических процессах, теплота Q, подводимая к системе, расходуется на совершение работы А и на изменение внутренней энергии Δ U

Q = A + D U. (1)

Теплота – это количество энергии хаотического движения, передаваемое термодинамической системе. Подвод теплоты приводит к повышению температуры:   , где n – количество газа, С − молярная теплоемкость, зависящая от вида процесса. Внутренняя энергия идеального газа — это кинетическая энергия молекул. Она пропорциональна температуре:   , где C_v– молярная теплоемкость при изохорическом нагревании. Работа элементарного изменения объема силами давления равна произведению давления на изменение объема: dA= PdV.

Для адиабатического процесса, происходящего без теплообмена (Q = 0), работа совершается за счет изменения внутренней энергии, A = − D U. При адиабатическом расширении работа газа положительна, поэтому внутренняя энергия и температура понижаются. При сжатии – наоборот. Все быстро протекающие процессы можно достаточно точно считать адиабатическими.

Выведем уравнение адиабатического процесса идеального газа. Для этого применим уравнение первого начала термодинамики для элементарного адиабатического процесса dA= − dU, которое принимает вид РdV =−n С_vdT . Добавим к этому дифференциальному уравнению еще одно, полученное дифференцированием уравнения Менделеева–Клапейрона (PV=νRT): PdV +VdP =nR dT. Исключая в двух уравнениях один из параметров, например, температуру, получим соотношение для двух других параметров 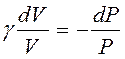  . Интегрируя и потенцируя, получим уравнение адиабаты через давление и объем:

P V ^g = const.

Аналогично:

T V ^g -1 = const, P ^g -1 T^--g = const. (2)

Здесь 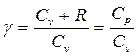  – показатель адиабаты, равный отношению теплоемкостей газа при изобарическом и изохорическом нагревании.

Получим формулу для показателя адиабаты в молекулярно-кинетической теории. Молярная теплоемкость по определению — это количество теплоты, необходимое для нагревания одного моля вещества на один Кельвин 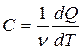  . При изохорическом нагревании теплота расходуется только на повышение внутренней энергии   . Подставив теплоту, получим   .

Приизобарическом нагревании газа в условиях постоянного давления дополнительно часть теплоты расходуется на работу изменения объема 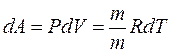  . Поэтому количество теплоты, (dQ = dU + dA) полученное при изобарическом нагревании на один Кельвин будет равно   . Подставив в формулу теплоемкости, получим   .

Тогда показатель адиабаты может быть определен теоретически по формуле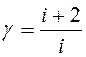

 . (3)

 

Здесь i – число степеней свободы молекул газа. Это число координат, достаточное для определения положения молекулы в пространстве или число составляющих компонентов энергии молекулы. Например, для одноатомной молекулы кинетическая энергия может быть представлена как Cvмма трех компонентов энергии, соответствующих движению вдоль трех осей координат, i = 3. Для жесткой двухатомной молекулы следует добавить еще два компонента энергии вращательного движения, так как энергия вращения относительно третьей оси, проходящей через атомы, отCvтствует. Итак, для двухатомных молекул i = 5. Для воздуха как для двухатомного газа теоретическое значение показателя адиабаты будет равно g = 1,4.

Показатель адиабаты можно определить экспериментально методом Клемана – Дезорма. В баллон нагнетают воздух, сжимая до некоторого давления Р₁ , немного больше атмосферного. При сжатии воздух несколько нагревается. После установления теплового равновесия баллон на короткое время открывают. В этом процессе расширения 1–2 давление падает до атмосферного Р₂=Р_атм, а исследуемая масса газа, которая до этого занимала часть объема баллона V₁, расширяется, занимая весь баллон V₂ (рис.1). Процесс расширения воздуха (1−2) происходит быстро, его можно считать адиабатическим, происходящим по уравнению (2)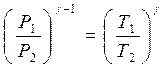

 . ( 4)

 

В адиабатическом процессе расширения воздух охлаждается. После закрытия клапана охлажденный воздух в баллоне через стенки баллона нагревается до температуры лаборатории Т ₃= Т₁. Это изохорический процесс 2–3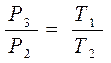

 . (5)

 

Решая совместно уравнения (4) и (5), исключая температуры, получим уравнение, 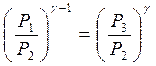  , из которого следует определить показатель адиабаты γ. Датчик давления измеряет не абсолютное давление, которое записано в уравнениях процессов, а избыточное над атмосферным давлением. То есть Р₁ = ΔР₁+ Р₂, и Р₃ =ΔР₃+Р₂.

Для понимания этого соотношения можно рассмотреть следующий эксперимент. Закрытый цилиндр с закреплённым неподвижно поршнем содержит воздух. Давление внутри равно давлению снаружи. Этот цилиндр нагревается до определённой, требуемой температуры. До тех пор, пока поршень закреплён в неподвижном состоянии, объём воздуха в цилиндре остаётся неизменным, в то время как температура и давление возрастают. Когда требуемая температура будет достигнута, нагревание прекращается. В этот момент поршень «освобождается» и, благодаря этому, начинает перемещаться под давлением воздуха в цилиндре без теплообмена с окружающей средой (воздух расширяется адиабатически).

Совершая работу, воздух внутри цилиндра охлаждается ниже достигнутой ранее температуры. Чтобы вернуть воздух к состоянию, когда его температура опять достигнет упомянутого выше требуемого значения (при всё ещё «освобождённом» поршне) воздух необходимо нагреть. Для этого нагревания извне необходимо подвести примерно на 40 % (для двухатомного газа — воздуха) большее количество теплоты, чем было подведено при предыдущем нагревании(с закреплённым поршнем).

В этом примере количество теплоты, подведённое к цилиндру при закреплённом поршне, пропорционально Cv, тогда как общее количество подведённой теплоты пропорционально Ср. Таким образом, показатель адиабаты в этом примере равен 1,4. Другой путь для понимания разницы между Ср и Cv состоит в том, что Ср применяется тогда, когда работа совершается над системой, которую принуждают к изменению своего объема (то есть путём движения поршня, который сжимает содержимое цилиндра), или если работа совершается системой с изменением её температуры (то есть нагреванием газа в цилиндре, что вынуждает поршень двигаться). Cv применяется только если совершённая газом работа — равна нулю.

Рассмотрим разницу между подведением тепла при закреплённом поршне и подведением тепла при освобождённом поршне. Во втором случае давление газа в цилиндре остаётся постоянным, и газ будет как расширяться, совершая работу над атмосферой, так и увеличивать свою внутреннюю энергию (с увеличением температуры); теплота, которая подводится извне, лишь частично идёт на изменение внутренней энергии газа, в то время как остальное тепло идёт на совершение газом работы.

Заключение

Подводя итоги всему вышесказанному, мы рассмотрели показатель адиабаты, а так же, как определяется соотношения с использованием количества степеней свободы. Так же в ходе работы было продемонстрированно, где применяется показатель адиабаты и основной принцип его работы.

Список использованной литературы

1. Иродов И.Е. Физика макросистем. Основные законы: Учебное пособие для физич. и инж.-технич. спец. вузов. – 4-е изд. – М.: БИНОМ. Лаборатория знаний, 2019. – 207 с.

2. Савельев И.В. Курс общей физики в 4-х томах. Механика. Молекулярная физика и термодинамика. – М.: КноРус, 2017. – Т.1. – 528 с.

3. Сивухин Д.В. Общий курс физики. Термодинамика и молекулярная физика. – М.: ФИЗМАТЛИТ, 2018. – Т.2. – 544 с. 5. Трофимова Т.И. Курс физики. – 20-е изд., стер. – М.: Изд-во «Академия», 2018. – 560 с. 6. Яворский Б.М., Детлаф А.А. Курс физики. – 9-е изд., стер. – М.: Изд-во «Академия», 2014. – 720 с.