Курсовая. Курсовая термех. Российский университет дружбы народов
 Скачать 21.69 Kb. Скачать 21.69 Kb.
|
|
Федеральное государственное бюджетное учреждение высшего образования РОССИЙСКИЙ УНИВЕРСИТЕТ ДРУЖБЫ НАРОДОВ (РУДН) ИНЖЕНЕРНАЯ АКАДЕМИЯ Направление 21.03.01 «Нефтегазовое дело» Курсовая работа по Теоретической и прикладной механике Выполнил: студент 2 курса Группы ИНГбд-02-20 Хуршидов Эсат Расимович Студ.номер 1032203677 Проверил: Ольфати Р.С. Москва 2022 Тема «Сопротивление материалов. Расчёт статически неопределимого бруса на растяжение (сжатие)». Вариант 8
Для стального бруса (см. рисунок), нагруженного силой F и собственным весом (γ = 7, 85 г/см3 ), требуется: 4. Определить опорные реакции в заделках. 5. Построить эпюры нормальных сил и нормальных напряжений по длине бруса. 6. Указать положение наиболее опасного сечения и величину нормального напряжения в этом сечении. 7. Проверить эпюру нормальных напряжений (площадь эпюры со знаком (+) должна равняться площади эпюры со знаком (-)). Принять, что материал бруса имеет модуль продольной упругости E = 2 ∙ 105 МПа. Решение: Выбираем основную систему, которая должна представлять собой статически определимую неизменяемую систему. Основная система получается из заданной системы путем отбрасывания лишних связей и замены их действия неизвестными реакциями. Принятая основная система показана на рис. 2 б. Строим эпюру нормальных сил N для основной системы, для чего определяем нормальные силы в соответствующих сечениях (Рис.2 б). 𝑁̅𝑎−𝑎 = 𝐴 ∙ 𝛾 ∙ 𝑐 = 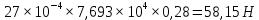 𝑁̅в−в = 𝑁̅𝑎−𝑎 + 𝐹 = 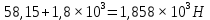 𝑁̅г−г = 𝑁̅в−в + 𝐴 ∙ 𝛾 ∙ 𝑏 = 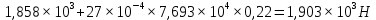 𝑁̅д−д = 𝑁̅г−г + 2 ∙ 𝐹 = 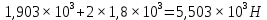 𝑁̅е−е = 𝑁̅д−д + 𝐴 ∙ 𝛾 ∙ 𝑎 = 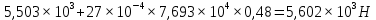 2) Определяем перемещение нижнего конца стального стеnржня основной системы: 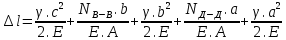 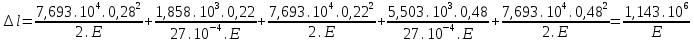 Таким образом, если в статически неопределимом брусе (Рис.2 а) убрать одну нижнюю опору, то нижнее опорное сечение переместится вниз на величину ∆𝑙, но этого в реальном брусе не может быть, следовательно, на опоре В должна действовать опорная реакция 𝑅𝐵, от которой будет возникать линейная деформация ∆𝑙𝐵, равная по величине ∆𝑙, но противоположная по знаку: 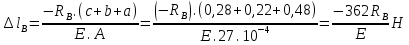 Уравнение перемещений будет иметь вид: ∆𝑙 + ∆𝑙𝐵 = 0 → 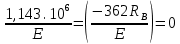 Из данного выражения находим 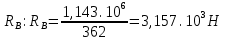 Опорная реакция 𝑅𝐵, вызывает в брусе сжатие, следовательно эпюра , нормальных сил от действия только опорной реакции 𝑅𝐵, будет иметь вид прямоугольника (Рис.2 г). Для получения эпюры нормальных сил для статически неопределимого бруса (рис. 2 а) следует сложить две эпюры: эпюру нормальных сил в основной системе и эпюру нормальных сил от действия опорной реакции 𝑅𝐵. Сложение эпюр проводим, складывая значения нормальных сил двух эпюр в соответствующих точках (рис.2 д). 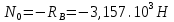 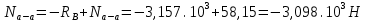 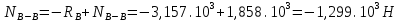 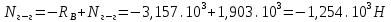 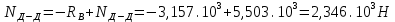 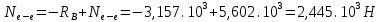 Вычисляем нормальные напряжения и строим их эпюры: 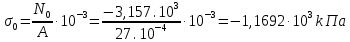 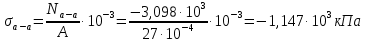 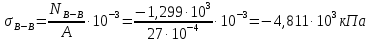 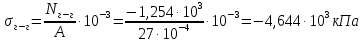 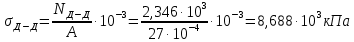 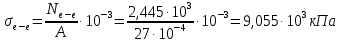 Эпюра нормальных напряжений σ показывает, что самое большое сжимающее нормальное напряжение будет в нижнем опорном сечении (𝜎𝑐,𝑚𝑎𝑥 = 𝜎0 = 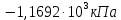 ) , а самое большое растягивающее напряжение - в верхнем опорном сечении (𝜎𝑡,𝑚𝑎𝑥 = 𝜎е−е = ) , а самое большое растягивающее напряжение - в верхнем опорном сечении (𝜎𝑡,𝑚𝑎𝑥 = 𝜎е−е =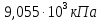 ). ). По эпюре нормальных сил находим опорную реакцию в верхней заделке 𝑅𝑐 = 𝑁е−е =  . . Критерием правильности вычислений является равенство нулю площади эпюры нормальных напряжений, т.е 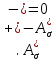 или или , где: , где: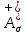 -площадь части эпюры нормальных напряжений со знаком «плюс». -площадь части эпюры нормальных напряжений со знаком «плюс».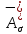 - площадь части эпюры нормальных напряжений со знаком «минус». - площадь части эпюры нормальных напряжений со знаком «минус». 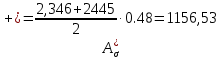 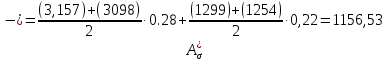 В нашем случае, 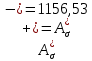 , следовательно, расчёт выполнен правильно. , следовательно, расчёт выполнен правильно. Ответ. 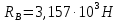 , , 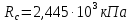 , , 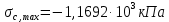 , , 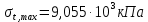 |
