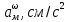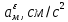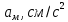механика Применение основных теорем динамики к исследованию движения материальной точки. Применение основных теорем динамики к исследованию движения мате. Российской федерации федеральное государственное бюджетное
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
|
1.4. Теорема о кинетической энергии материальной точки Кинетической энергией движущейся материальной точки называется скалярная величина, равная половине произведения массы движущейся точки на квадрат ее скорости. Кинетическая энергия имеет размерность работы и измеряется в системе СИ в Джоулях [Дж]. Теорема: Изменение кинетической энергии движущейся материальной точки равно работе приложенной к ней силы не пройденном этой точкой пути. Доказательство: Пусть материальная точка М массы  движется под действием силы движется под действием силы  по некоторой криволинейной траектории (рис.20.4). по некоторой криволинейной траектории (рис.20.4).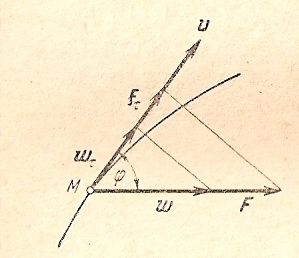 Рис.20.4. Рис.20.4.Напишем основное уравнение динамики, выражающее второй закон Ньютона:  . Проектируя это векторное равенство на направление скорости . Проектируя это векторное равенство на направление скорости  , получим: , получим: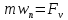 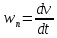 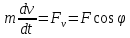 Где φ – угол между векторами  и и  . Умножая обе части этого равенства на . Умножая обе части этого равенства на 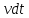 получим: получим: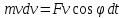 Или 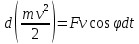 Правая часть этого равенства представляет собой элементарную работу силы  . Следовательно, дифференциал кинетической энергии материальной точки равен элементарной работе силы, действующей на эту точку. . Следовательно, дифференциал кинетической энергии материальной точки равен элементарной работе силы, действующей на эту точку.Этот результат выражает теорему о кинетической энергии в дифференциальной форме. Интегрируя, полученное уравнение в соответствующих пределах, получим: 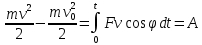 1.5. Понятие о потенциальной энергии Пусть материальная точка, движущаяся в потенциальном силовом поле, находится в точке М(х,у,z), в которой силовая функция имеет значение U,и пусть точка М(0)(х(0),у(0),z(0)) будет какая-либо произвольно выбранная неподвижная (нулевая) точка, в которой силовая функция имеет значение: 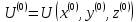 Работа, производимая силой поля при перемещении материальной точки из положения М в «нулевую точку» М(0), называется потенциальной энергией в точке М. 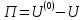 В нулевой точке М(0) потенциальная энергия равна нулю. За нулевую точку можно принять любую точку поверхности уровня, на которой силовая функция имеет значение 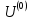 . .Пусть материальная точка находится в поле силы тяжести. Примем произвольно взятую горизонтальную плоскость за нулевую и будем считать потенциальную энергию на этой плоскости равной нулю. Потенциальная энергия в точке М, находящейся на высоте 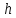 над этой нулевой плоскостью равна над этой нулевой плоскостью равна 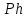 , где Р – вес данной материальной точки. , где Р – вес данной материальной точки.Так как 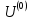 величина постоянная, то: величина постоянная, то: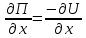 , , 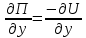 , , 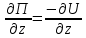 Отсюда: 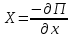 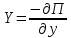 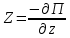 Проекции силы потенциального поля на координатные оси равны взятым с обратным знаком частным производным от потенциальной энергии по соответствующим координатам. 1.6. Закон сохранения энергии Пусть М1 и М2 – два различных положения материальной точки, движущейся в потенциальном силовом поле, и 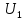 и и 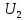 - соответствующие значения силовой функции в этих точках. Изменение кинетической энергии точки будет равно работе приложенной к ней силы: - соответствующие значения силовой функции в этих точках. Изменение кинетической энергии точки будет равно работе приложенной к ней силы: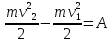 Где 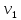 и и 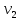 - скорости движущейся точки в положениях М1 и М2. Но так как работа А равна разности значений силовой функции в конечном и начальном положениях движущейся точки, то - скорости движущейся точки в положениях М1 и М2. Но так как работа А равна разности значений силовой функции в конечном и начальном положениях движущейся точки, то 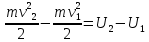 Потенциальная энергия в точках М1 и М2 будет равна: 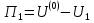 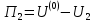 Откуда: 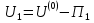 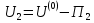 Подставляя эти значения в уравнение кинетической энергии, получим: 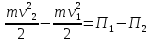 Или 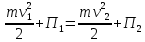 Т.е. 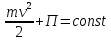 При движении материальной точки в потенциальном силовом поле сумма кинетической и потенциальной энергии остается постоянной. Этот результат, выражающий закон сохранения механической энергии, представляет собой частный случай общего физического закона сохранения энергии. Практическая часть Дано: 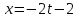 ; ; 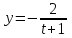 ; ; 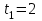 с сНайти: уравнение траектории точки, а также для момента времени t = t1 (с) определить положение точки на траектории, ее скорость, полное, касательное и нормальнее ускорения, радиус кривизны траектории в соответствующей точке РЕШЕНИЕ: 1. Уравнение траектории. Определим уравнение траектории точки в координатной форме, исключив время из уравнений движения. Из первого уравнения 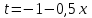 Подставляем найденное выражение во второе уравнение и получаем уравнение траектории 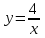 Это уравнение гиперболы. Положение точки при 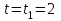 с: с: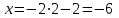 (см), (см), 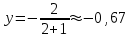 (см) (см)2. Скорость точки. Скорость найдем по ее проекциям на координатные оси: 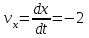 , , 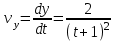 При 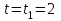 с: с: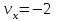 (см/с), (см/с), 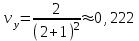 (см/с) (см/с)Модуль скорости: 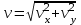 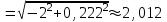 (см/с) (см/с)3. Ускорение точки. Находим аналогично: 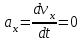 , , 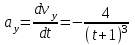 При 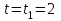 с: с: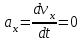 , , 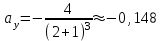 (см/с2) (см/с2)Модуль ускорения: 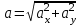 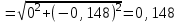 (см/с2) (см/с2)4. Касательное ускорение. Используем формулу 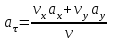 При 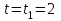 с: с: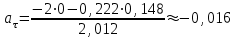 (см/с2) (см/с2)5. Нормальное ускорение. 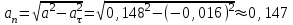 (см/с2) (см/с2)6. Радиус кривизны траектории. 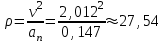 (см) (см)
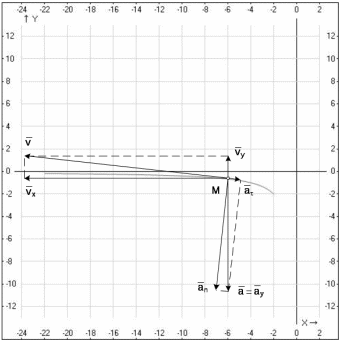 Задача 2 «Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях» Движение груза 1 должно описываться уравнением 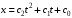 , ,где 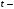 время (с), c0, с1, с2, -некоторые постоянные. время (с), c0, с1, с2, -некоторые постоянные. В начальный момент времени (t=0) положение груза определяется координатой 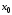 , и он имеет скорость , и он имеет скорость 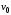 . Учесть, что в момент времени . Учесть, что в момент времени 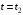 координата груза равна координата груза равна 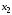 . .Определить коэффициенты С0,С1,С2, при которых осуществляется требуемое движения груза 1. Определить также момент времени t=t1 скорость и ускорение груза и точки М одного из колес механизма. Схема см. (Приложение А, Рисунок 3): Дано: 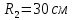 , , 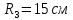 , , 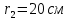 , , 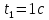 , , 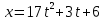 Найти уравнения движения груза, а также скорости и ускорения груза и точки М в момент времени 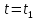 . .Решение: 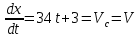 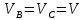 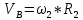 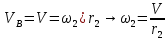 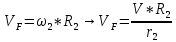 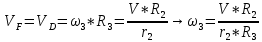 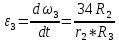 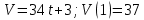 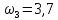 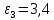 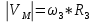 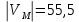 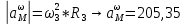 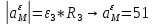 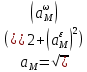 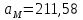
Дано: Точка М движется относительно тела D. Уравнение относительного движения т. М: 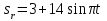 (см). Уравнение движения тела (см). Уравнение движения тела 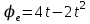 (рад). t=2/3 с; =30о. (рад). t=2/3 с; =30о.Найти: Для заданного момента времени определить абсолютную скорость и абсолютное ускорение т.М. РЕШЕНИЕ: П 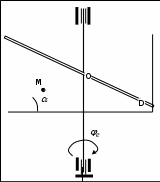 оложение т.М на теле D определяется расстоянием оложение т.М на теле D определяется расстоянием 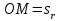 . . При t=2/3с 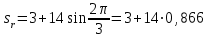 =15,1 (см). =15,1 (см).Абсолютную скорость т.М найдем как геометрическую сумму относительной и переносной скоростей: 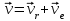 Относительная скорость 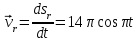 При 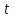 =2/3с =2/3с 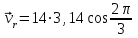 = 22(см/с) – вектор направлен в сторону отрицательных значений = 22(см/с) – вектор направлен в сторону отрицательных значений 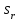 . .Модуль относительной скорости 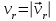 =22 см/с. =22 см/с.М 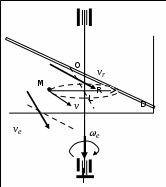 одуль переносной скорости одуль переносной скорости 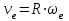 , , где R - радиус окружности L, описываемой той точкой тела, с которой совпадает в данный момент т.М 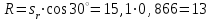 (см); (см); | ||||||||||||||||||||||||||||||||||||||||||||||

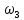 рад/с
рад/с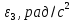
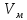 ,см/с
,см/с