Тип. расчет №8 (11-20). Розрахунок 8 теорія ймовірностей варіант 11. Класичне визначення ймовірності

• Название: Розрахунок 8 теорія ймовірностей варіант 11. Класичне визначення ймовірності
• Анкор: Тип. расчет №8 (11-20).doc
• Дата: 16.08.2018
• Размер: 423.5 Kb.
• Имя файла: Тип. расчет №8 (11-20).doc
• Тип: Розрахунок; #23089

Донбаська державна академія будівництва та архітектури

Напрям: 0921 “Будівництво” Семестр IV

Навчальний предмет: “Вища математика”

Типовий розрахунок №8

ТЕОРІЯ ЙМОВІРНОСТЕЙ

Варіант 11.
1. Класичне визначення ймовірності.

В урні 12 куль, які нічим, крім кольору, не відрізняються. Серед цих куль 5 чорних і 7 білих. Яка ймовірність того, що дві вийнятих кулі однокольорові? Різнокольорові?

2. Теореми додавання та множення.
Робітник обслуговує 4 станки. Ймовірність того, що протягом години перший станок не вимагатиме уваги робітника дорівнює 0,7, для другого станка ця ймовірність дорівнює 0,8, для третього - 0,9, для четвертого – 0,85. Знайти ймовірність того, що:

а) рівно один станок вимагатиме уваги робітника;

б) хоча б один вимагатиме уваги.

3. Формула повної ймовірності і формула Байєса.
Дві перфораторщиці набили на різних перфораторах по однаковому комплекту перфокарт. Ймовірність, що перша перфораторщиця припустила помилку дорівнює 0,05, для другої ця ймовірність дорівнює 0,1. Виявлена помилка. Знайти ймовірність того, що помилилась перша перфораторщиця?

4. Формула Бернуллі. Теорема Лапласа.

Ймовірність попадання в мішень при одному пострілі 0,8. Знайти ймовірності:

а) при 8 пострілах буде 6 влучень;

б) при 100 пострілах влучень 82;

в) при 200 пострілах влучень більше 150.

5. Дискретні випадкові величини.

Випадкова величина має розподіл:

	0	1	3	4
	0,3	0,2	0,1

Знайти:, , , ,, , , .

6. Неперервні випадкові величини.

Випадкова величина 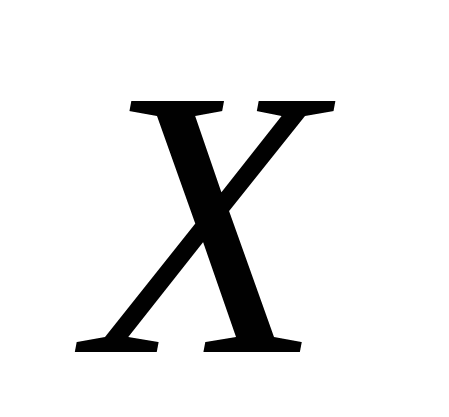задана щільністю розподілу:

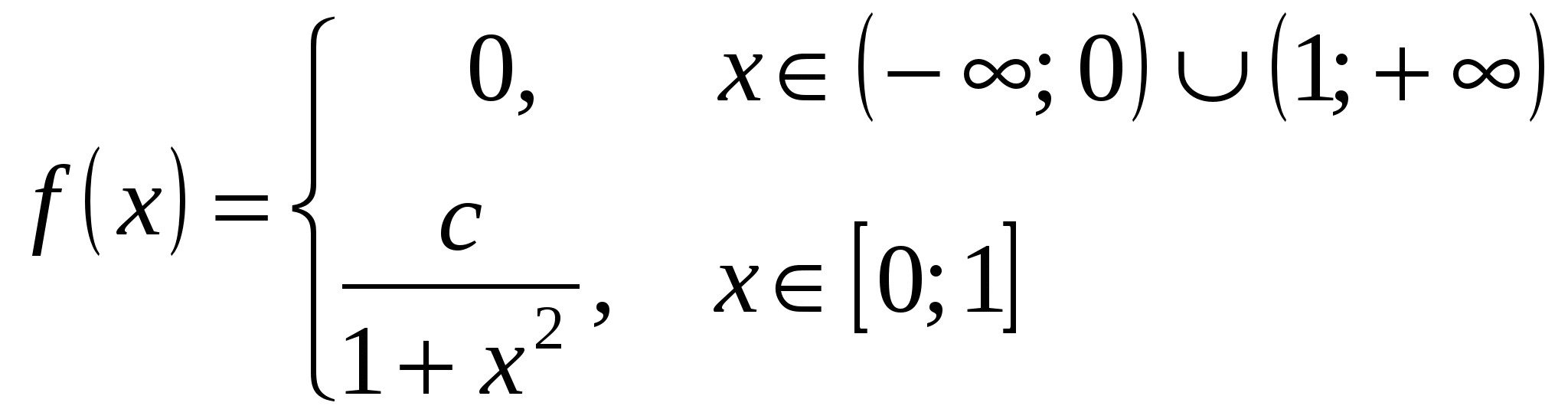
Обчислити: константу , ,, .

7. Нормальний розподіл.

Функція розподілу випадкової величини 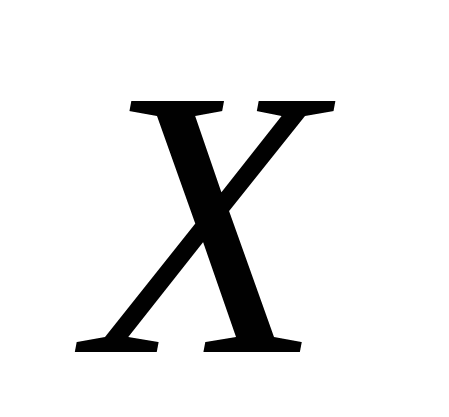має вигляд:

Знайти: ,, , .

Затверджено навчально-методичною комісією кафедри ВМіЕ протокол №3 від 22.02.2000 р.

Донбаська державна академія будівництва та архітектури

Напрям: 0921 “Будівництво” Семестр IV

Навчальний предмет: “Вища математика”

Типовий розрахунок №8

ТЕОРІЯ ЙМОВІРНОСТЕЙ

Варіант 12.
1. Класичне визначення ймовірності.

В коробці 15 куль: 5 червоних, 3 зелених, 7 білих. Випадково виймаються три з них. Знайти:

а) ймовірність того, що кулі різного кольору;

б) ймовірність того, що кулі мають однаковий колір;

в) серед куль дві червоних.

2. Теореми додавання та множення.

Формула існує в першому довіднику з ймовірністю 0,7, другому з ймовірністю 0,9, в третьому - з ймовірністю 0,6. Яка ймовірність того, що:

а) формула існує у всіх довідниках;

б) формула існує рівно в двох довідниках;

в) формула існує хоча б в одному довіднику.

3. Формула повної ймовірності і формула Байєса.
Існує двадцять екзаменаційних білетів. Якщо студент витягне один з перших 12 білетів, то він отримає відмітку “відмінно” з ймовірністю 0,6; якщо один з решти, то отримає відмітку “відмінно” з ймовірністю 0,3. Знайти:

а) ймовірність того, що студент отримає відмітку “відмінно”;

б) студент отримає відмітку “відмінно. Яка ймовірність того, що він витягнув один з перших 12 білетів?

4. Формула Бернуллі. Теорема Лапласа.

Подія в експерименті виникне з ймовірністю 0,3.

а) яка ймовірність того, що в 8 експериментах подія виникне 4 рази?

б) яка ймовірність того, що в 80 експериментах подія виникне рівно 30 разів?

в) яка ймовірність того, що в 80 експериментах подія виникне менше 30 разів?

5. Дискретні випадкові величини.

Закон розподілу випадкової величини 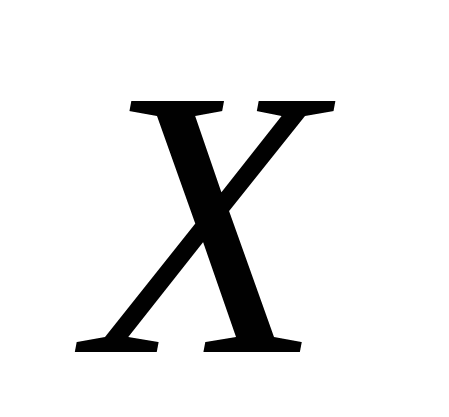має вигляд:

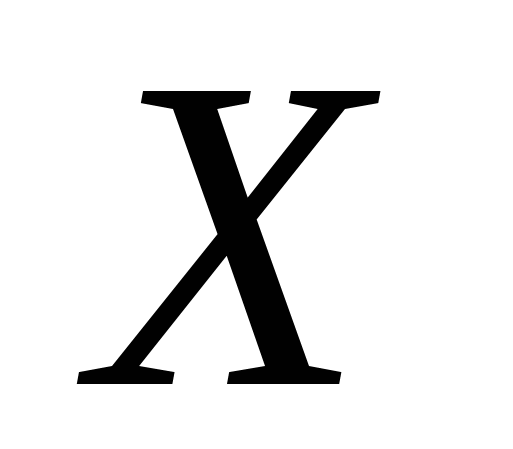
	-3	-2	-1	0	1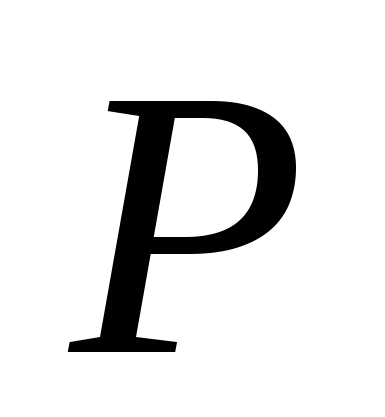
	0,2	0,1	0,2	0,3	0,2

Знайти: , , ,, , .

6. Неперервні випадкові величини.

Функція розподілу випадкової величини 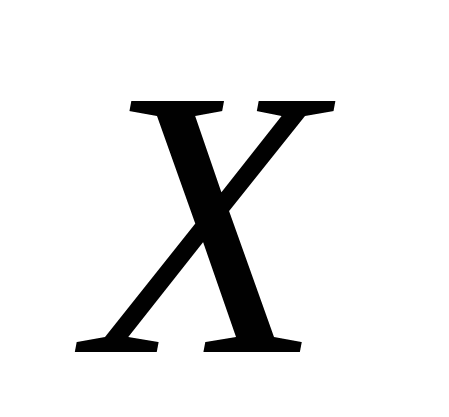має вигляд:

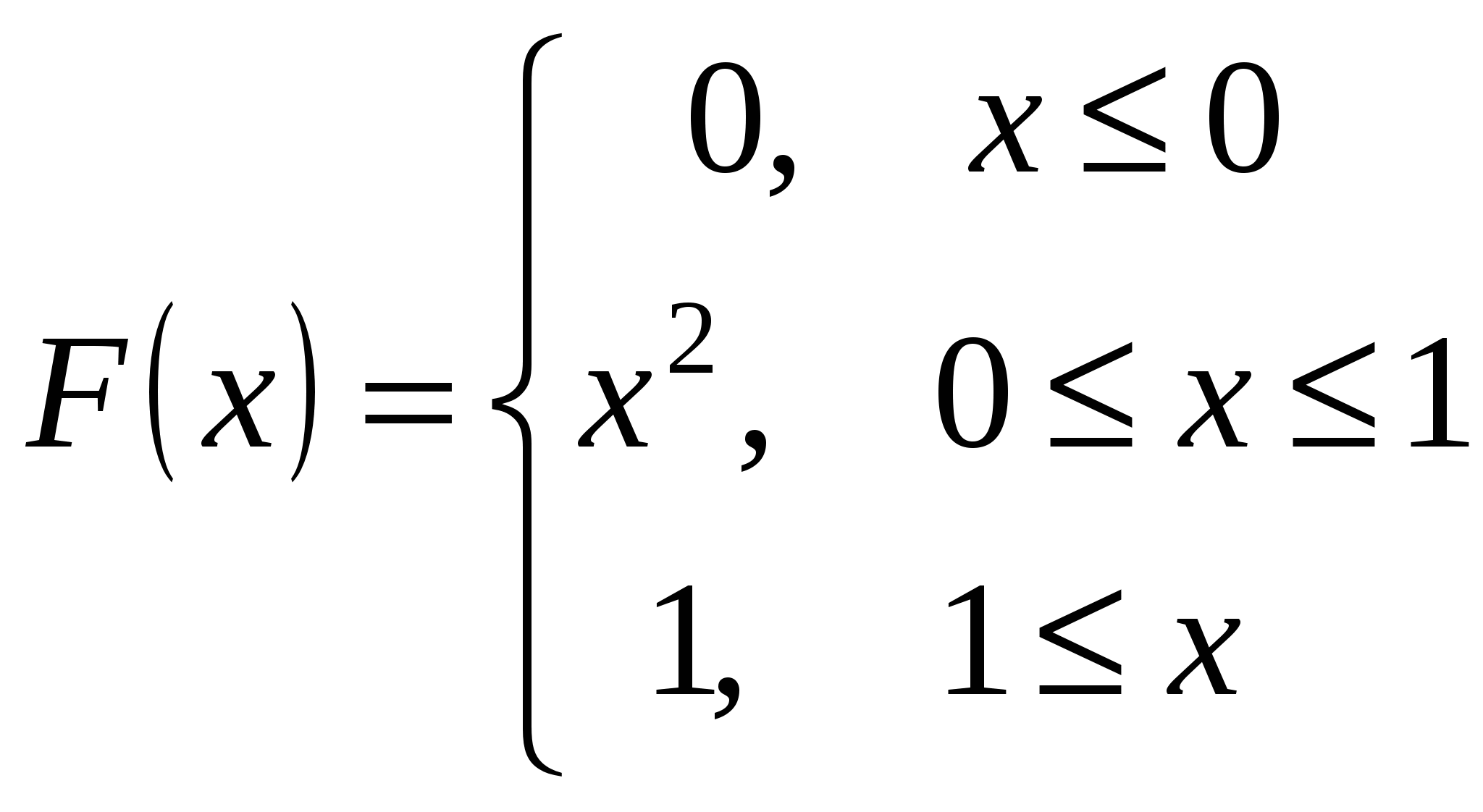
Знайти: щільність розподілу , ,, , .

7. Нормальний розподіл.
Випадкова величина має нормальний розподіл з параметрами , . Знайти:

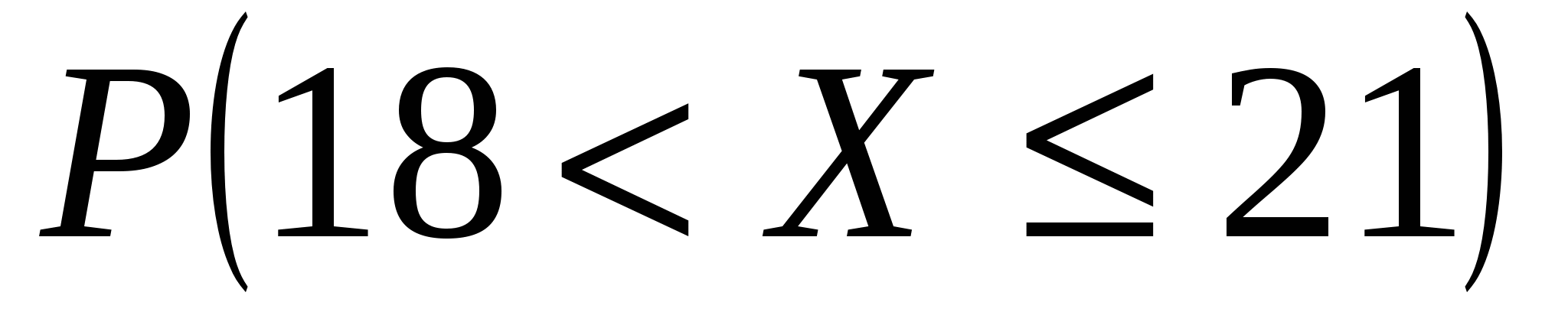а) ; б) .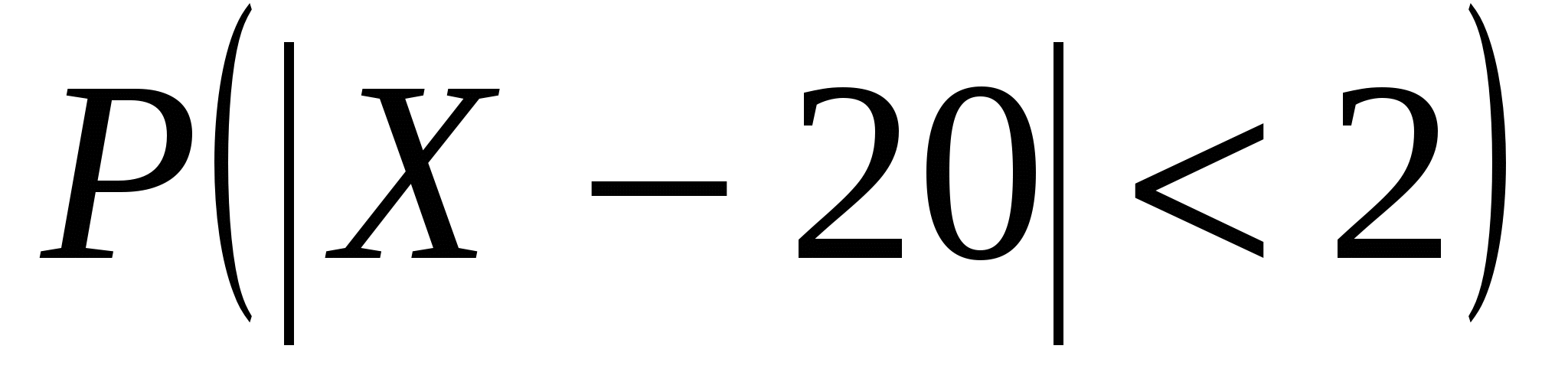

Затверджено навчально-методичною комісією кафедри ВМіЕ протокол №3 від 22.02.2000 р.

Донбаська державна академія будівництва та архітектури

Напрям: 0921 “Будівництво” Семестр IV

Навчальний предмет: “Вища математика”

Типовий розрахунок №8

ТЕОРІЯ ЙМОВІРНОСТЕЙ

Варіант 13.
1. Класичне визначення ймовірності.

З коробки, в якій лежать 10 шоколадних цукерок, 28 карамельок навмання виймають 5 цукерок. Знайти ймовірність, що серед цих п`яти цукерок буде:

а) 2 шоколадні цукерки;

б) 3 шоколадні цукерки;

в) хоча б одна шоколадна цукерка.

2. Теореми додавання та множення.

Три стрільці стріляють по цілі. Ймовірність, що в ціль попаде перший 0,7, другий - 0,6, третій - 0,3. Знайти ймовірність:

а) в ціль попаде тільки один з них;

б) всі попадуть в ціль;

в) хоча б один попаде в ціль.

3. Формула повної ймовірності і формула Байєса.
Електролампи виготовляються на 3 заводах. Перший завод виробляє 45% загальної кількості електроламп, другий – 40% , третій – 15%. Вироби першого заводу містять 70% стандартних ламп, другого – 80%, третього – 81%. В магазини надходить вироби всіх трьох заводів. Яка ймовірність, що куплена в магазині лампа виявиться стандартною?

а) знайти ймовірність того, що навмання взята деталь виявиться бракованою?

б) взята бракована деталь. Яка ймовірність того, що вона виготовлена першим заводом?

4. Формула Бернуллі. Теорема Лапласа.

Виріб стандартний з ймовірністю 0,7. Знайти ймовірності:

а) з 5 виробів 4 стандартні;

б) з 60 виробів 40 стандартних;

в) з 100 виробів стандартними виявиться більше 80 виробів.

5. Дискретні випадкові величини.

Закон розподілу випадкової величини має вигляд:

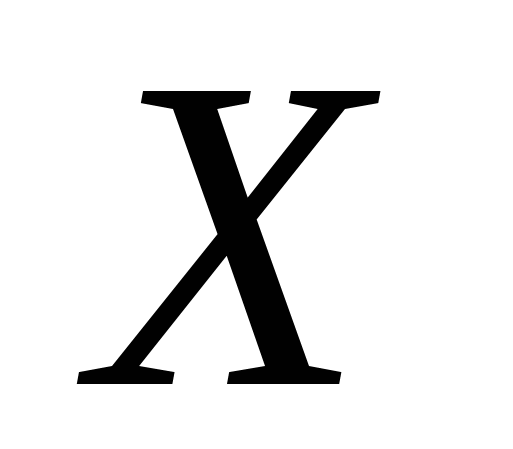
	-4	-1	0	4	9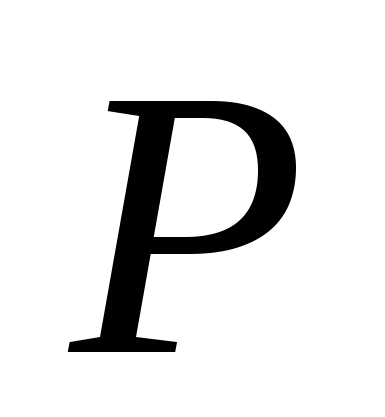
	0,2	0,1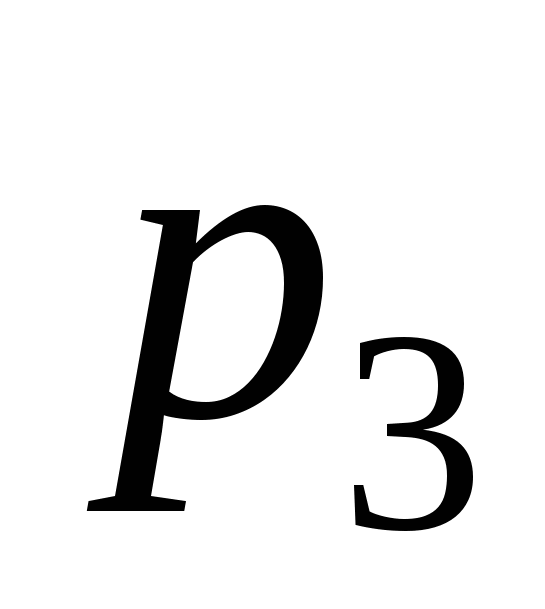		0,2	0,1

Знайти: , ,, , , ,, .

6. Неперервні випадкові величини.

Функція розподілу випадкової величини має вигляд:

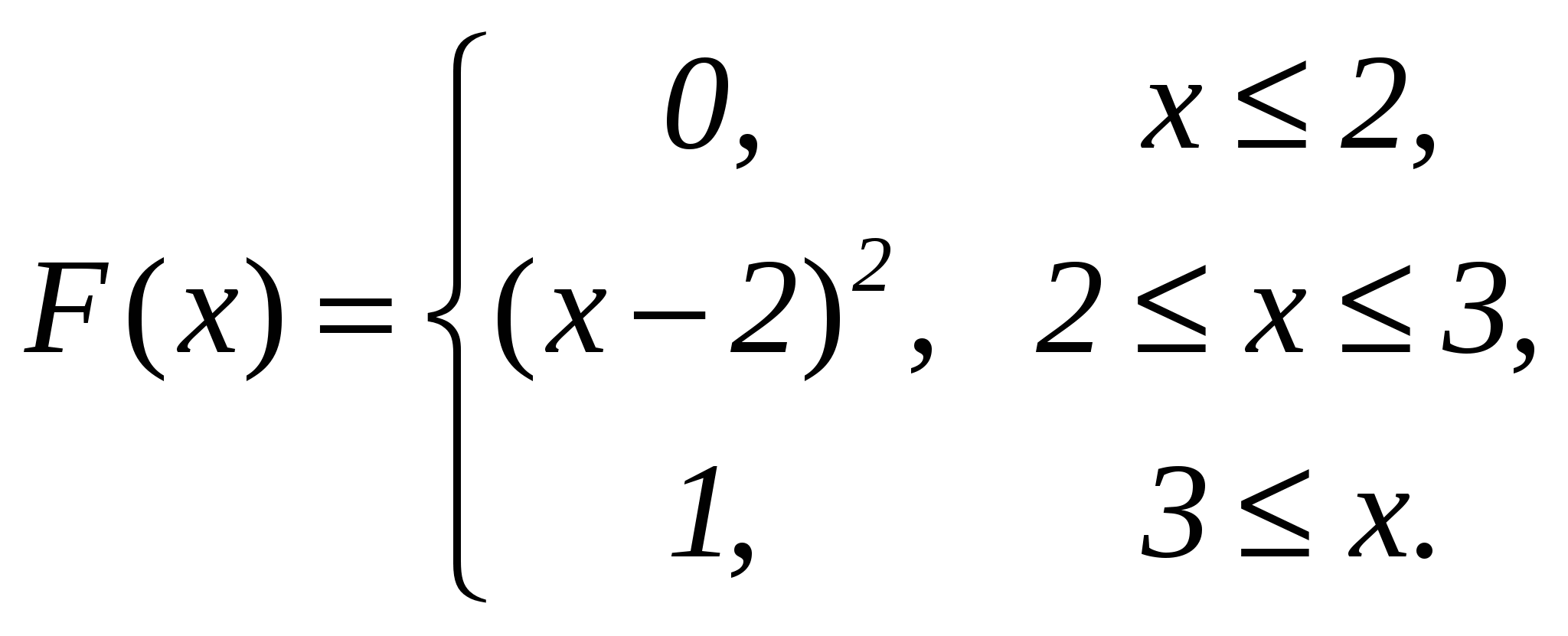
Знайти: , , .

7. Нормальний розподіл.
Вага виробу представляє собою випадкову величину, маючи нормальний розподіл з середнім значенням 900 г і середнім квадратичним відхиленням 10г. Знайти ймовірності, що: а) вага виробу знаходиться в межах від 880 до 910г.;

б) вага виробу відрізняється від середнього не більше, ніж на 5 г.

Затверджено навчально-методичною комісією кафедри ВМіЕ протокол №3 від 22.02.2000 р.

Донбаська державна академія будівництва та архітектури

Напрям: 0921 “Будівництво” Семестр IV

Навчальний предмет: “Вища математика”

Типовий розрахунок №8

ТЕОРІЯ ЙМОВІРНОСТЕЙ

Варіант 14.
1. Класичне визначення ймовірності.

В коробці 12 деталей, 3 з яких виготовлені заводом А, 4 - заводом В, решта - заводом С. Навмання виймають 5 деталей. Знайти ймовірність того, що:

а) 2 деталі виготовлені заводом А, 1  заводом В, 2 - заводом С;

б) три деталі виготовлені заводом С.

2. Теореми додавання та множення.

Ймовірність того, що шукана книжка існує в 1-й бібліотеці 0,8, в другій - 0,7, в третій - 0,4. Знайти ймовірності:

а) книжка існує в двох бібліотеках;

б) книжка існує тільки в одній бібліотеці;

в) книжка існує хоча б в одній бібліотеці.

3. Формула повної ймовірності і формула Байєса.
На складання потрапляють деталі з 3-х автоматів. Відомо, що перший автомат дає 0,3% браку, другий - 0,2% браку, третій - 0,4%. З першого автомату надійшло 1000, з другого - 2000 і з третього - 2500 деталей. Знайти ймовірності:

а) на складання потрапила бракована деталь;

б) відомо, що на складання потрапила бракована деталь.

Знайти ймовірність того, що вона надійшла з другого автомату.

4. Формула Бернуллі. Теорема Лапласа.

Ймовірність того, що покупець зробить покупку в магазині 0,3. Знайти ймовірності:

а) з 7 покупців покупку зроблять троє;

б) з 40 покупців покупку зроблять 14;

в) з 60 покупців покупку зроблять менше 20 покупців.

5. Дискретні випадкові величини.

Закон розподілу випадкової величини має вигляд:

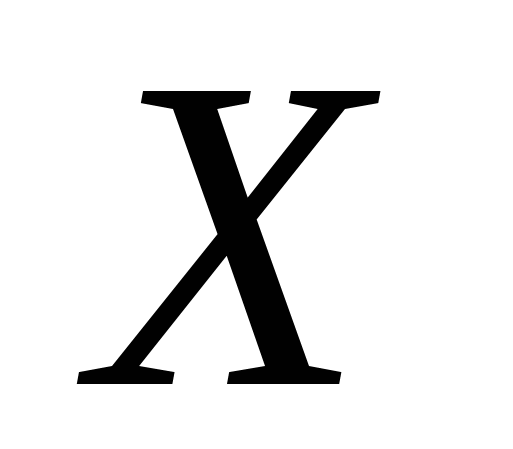
	-3	0	2	3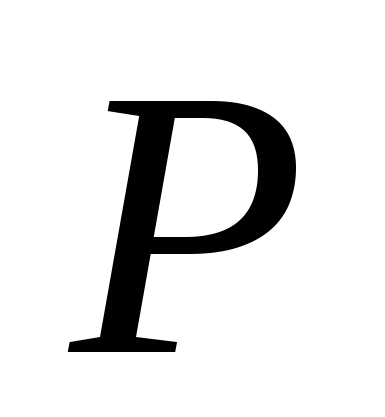
	0,2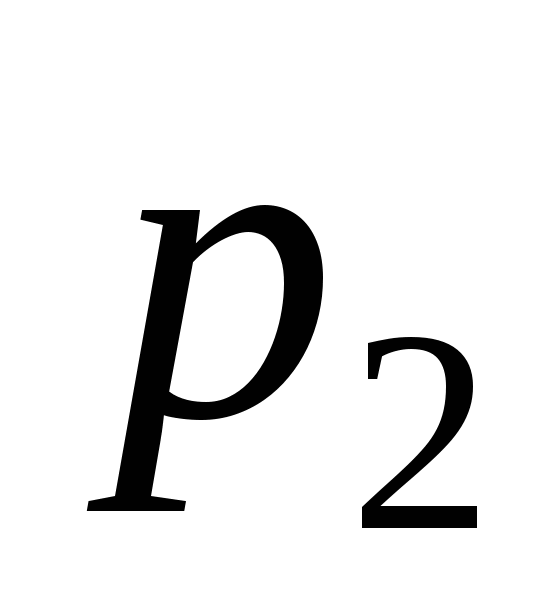		0,3	0,2

Знайти: , ,, ,, .

6. Неперервні випадкові величини.

Щільність розподілу випадкової величини має вигляд:

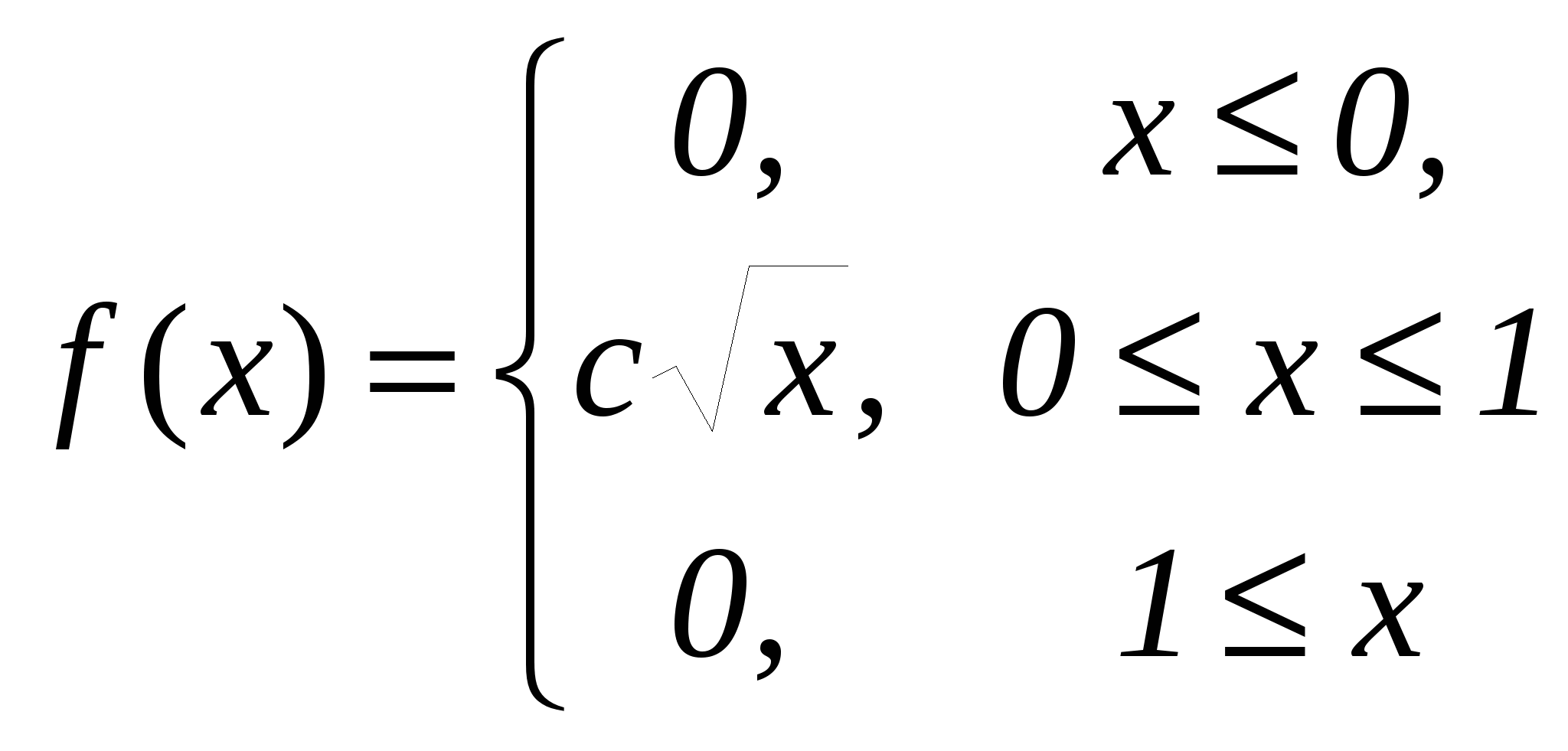
Знайти: параметр , ,, .

7. Нормальний розподіл.

Випадкова величина 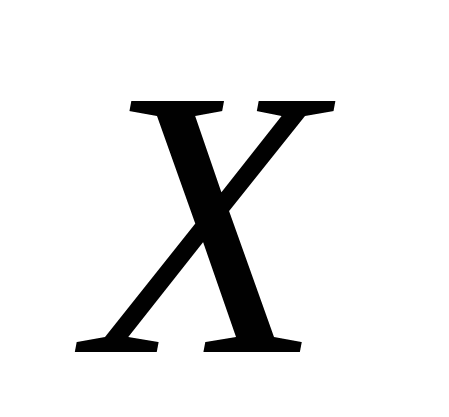має нормальний розподіл з середнім значенням 90 і дисперсією 9. Знайти ймовірність:

а) 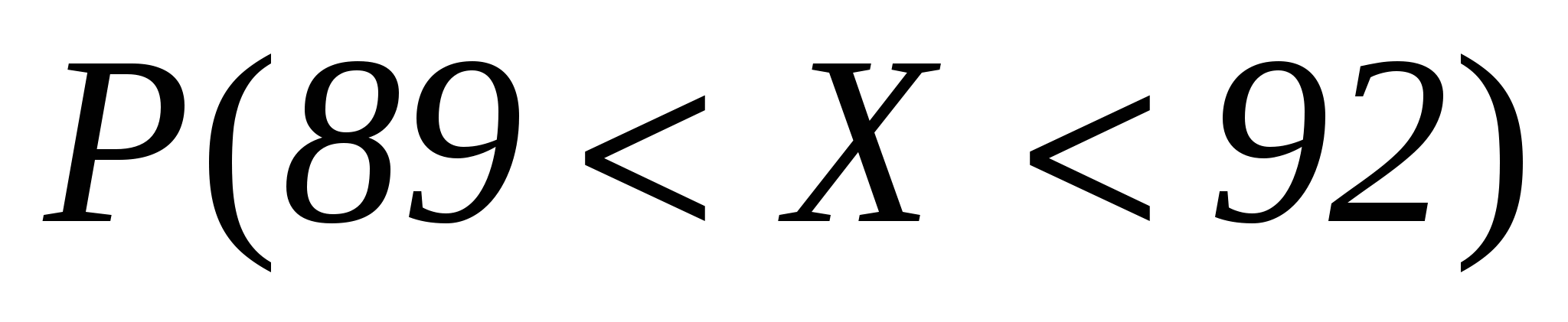; б) .

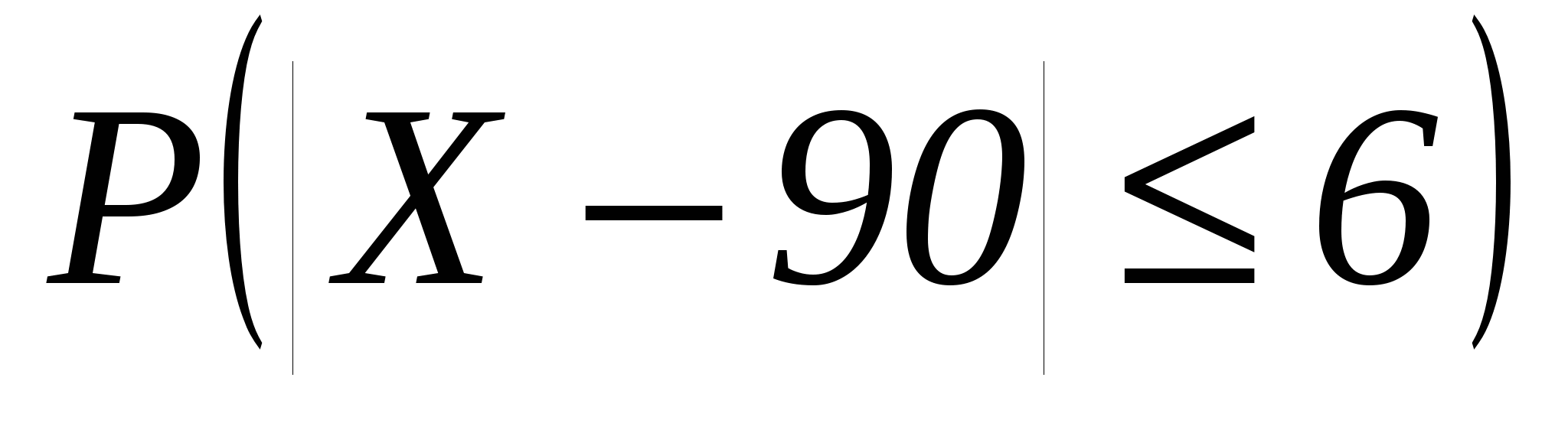Затверджено навчально-методичною комісією кафедри ВМіЕ протокол №3 від 22.02.2000 р.

Донбаська державна академія будівництва та архітектури

Напрям: 0921 “Будівництво” Семестр IV

Навчальний предмет: “Вища математика”

Типовий розрахунок №8

ТЕОРІЯ ЙМОВІРНОСТЕЙ

Варіант 15.
1. Класичне визначення ймовірності.

Серед 15 деталей 5 виготовлені 1-м заводом, 4 - другим і 6 - третім. Навмання беруть 3 деталі. Знайти ймовірності:

а) деталь виготовлена різними заводами;

б) деталі виготовлені одним заводом;

в) серед деталей рівно одна виготовлена першим заводом.

2. Теореми додавання та множення.

В магазині знаходиться 1 чоловік і 2 жінки. Чоловік купує товар з ймовірністю 0,1, жінка - з ймовірністю 0,5. Знайти ймовірності:

а) тільки один покупець купує товар;

б) всі покупці куплять товари;

в) хоча б один покупець купить товар.

3. Формула повної ймовірності і формула Байєса.
На склад надходять вироби 3 фабрик. Причому виріб першої фабрики складає 20%, другої - 46% і третьої - 34%. Відомо також, що середній процент нестандартних виробів для першої фабрики дорівнює 3%, для другої – 2% і для третьої – 1%. Знайти ймовірність того, що навмання взятий виріб виготовлено на першій фабриці, якщо він виявився нестандартним.
4. Формула Бернуллі. Теорема Лапласа.

Ймовірність того, що виріб придатний, дорівнює 0,85. Знайти ймовірності:

а) з 5 виробів всі придатні;

б) з 40 виробів 35 придатні;

в) з 100 виробів більше 80 придатні.

5. Дискретні випадкові величини.

Закон розподілу випадкової величини має вигляд:

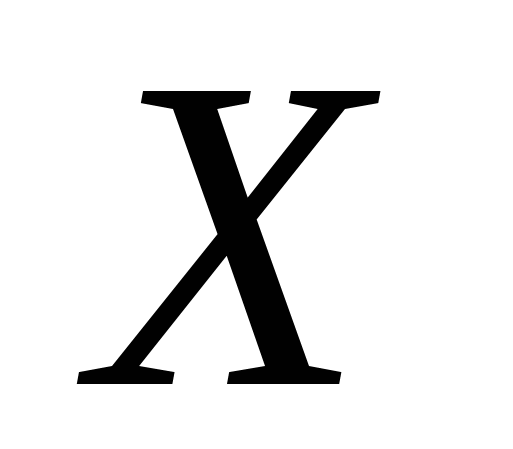
	-2	-1	0	1	2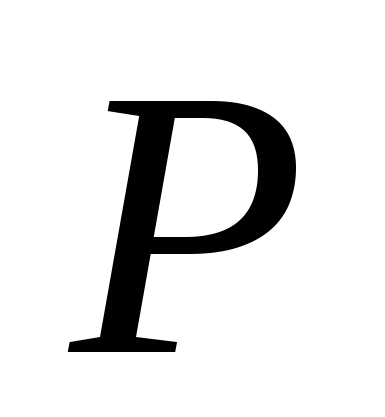
	0,3	0,1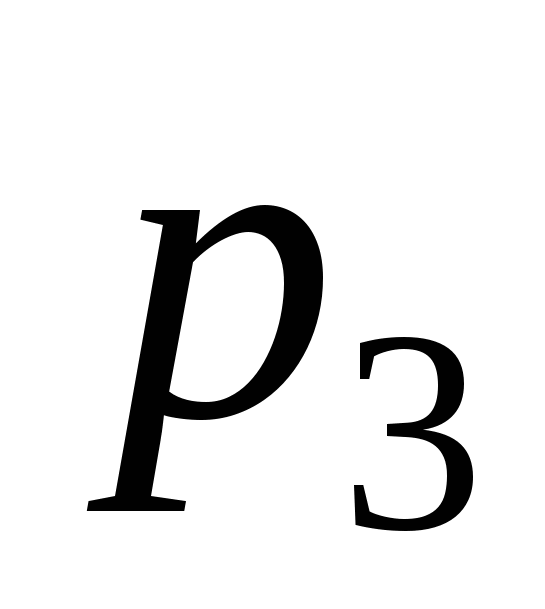		0,1	0,3

Знайти: , ,, , , .

6. Неперервні випадкові величини.

Щільність розподілу випадкової величини має вигляд:

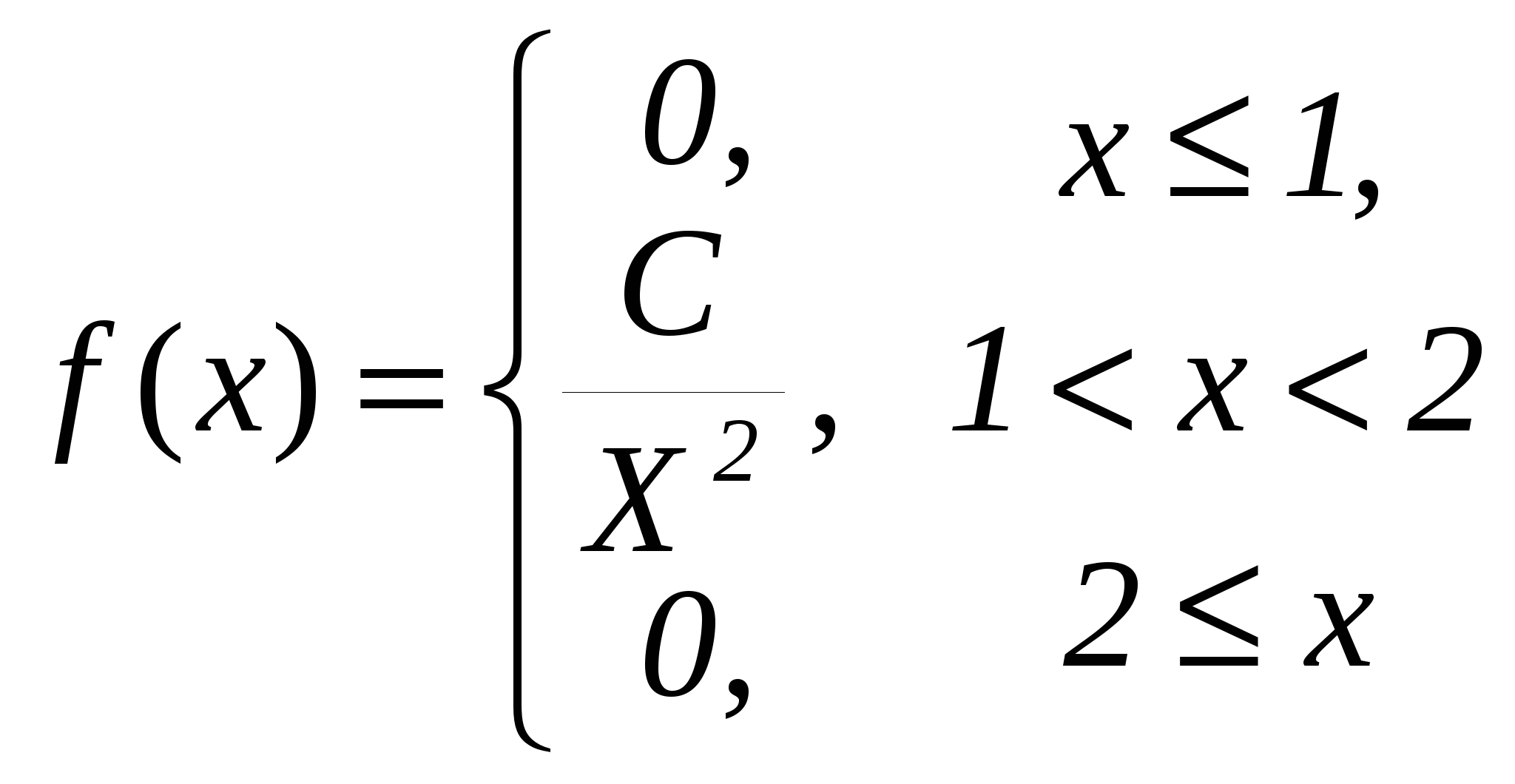
Знайти: параметр , ,, , .

7. Нормальний розподіл.
Випадкова величина має нормальний розподіл з параметрами ,. Знайти ймовірність того, що:

а) ;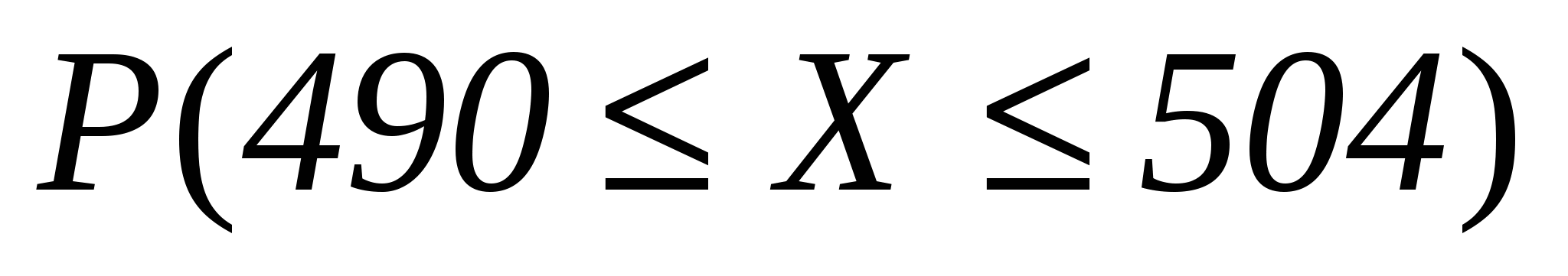

б) .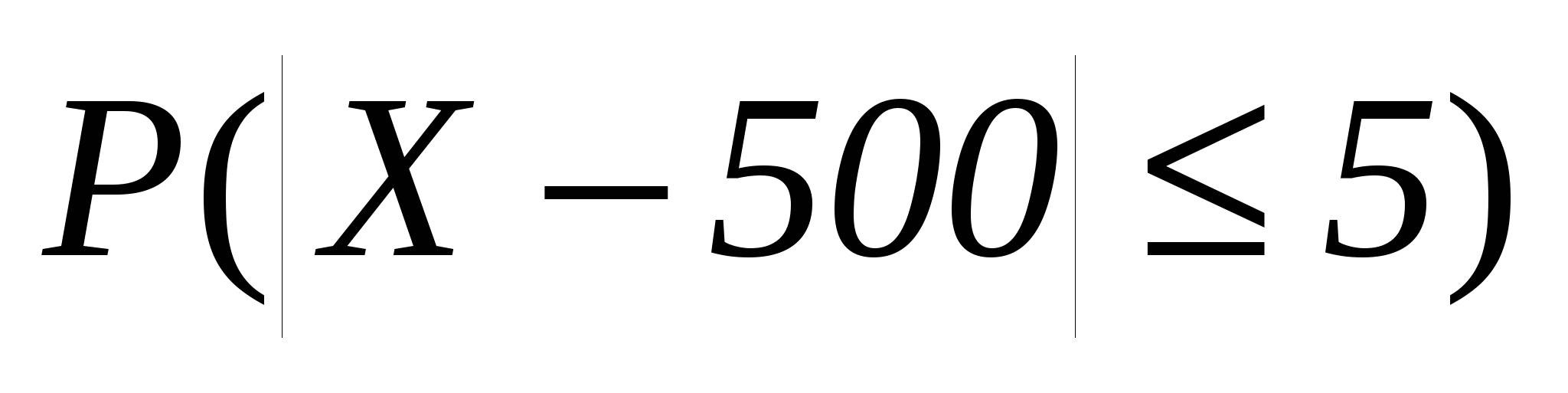

Затверджено навчально-методичною комісією кафедри ВМіЕ протокол №3 від 22.02.2000 р.

Донбаська державна академія будівництва та архітектури

Напрям: 0921 “Будівництво” Семестр IV

Навчальний предмет: “Вища математика”

Типовий розрахунок №8

ТЕОРІЯ ЙМОВІРНОСТЕЙ

Варіант 16.
1. Класичне визначення ймовірності.

В партії, складеній з 20 виробів, існує 3 дефектних. Для контролю обрали 5 виробів. Знайти ймовірності:

а) один виріб з перевірених виявився дефектним;

б) два вироби виявилися дефектними.

2. Теореми додавання та множення.
Робітник обслуговує три станки, які працюють незалежно один від одного. Ймовірність того, що протягом години не вимагатиме уваги перший станок 0,9, другий – 0,8, третій – 0,85. Знайти ймовірність того, що протягом години хоча б один станок вимагатиме уваги робітника.

3. Формула повної ймовірності і формула Байєса.
На складання потрапляють деталі з 3-х автоматів. Відомо, що перший автомат дає 0,3% браку, другий - 0,2% браку, третій - 0,4%. Знайти ймовірність потрапляння на складання бракованої деталі, якщо з першого автомату надійшло 1000, з другого - 2000 і з третього - 2500 деталей.

4. Формула Бернуллі. Теорема Лапласа.

Ймовірність народження дівчинки 0,49. Знайти ймовірності:

а) серед 5 немовлят 3 дівчинки;

б) серед 20 немовлят 8 дівчаток;

в) серед 100 немовлят дівчин більше 40, але не менше 55.

5. Дискретні випадкові величини.

Розподіл випадкової величини 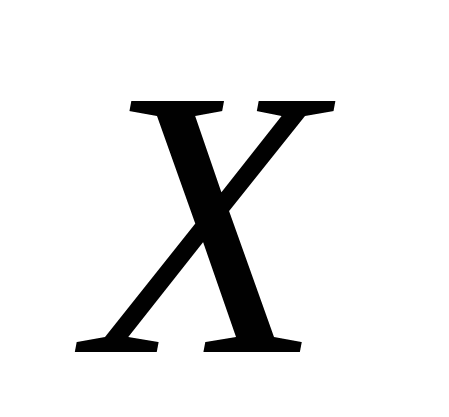має вигляд:

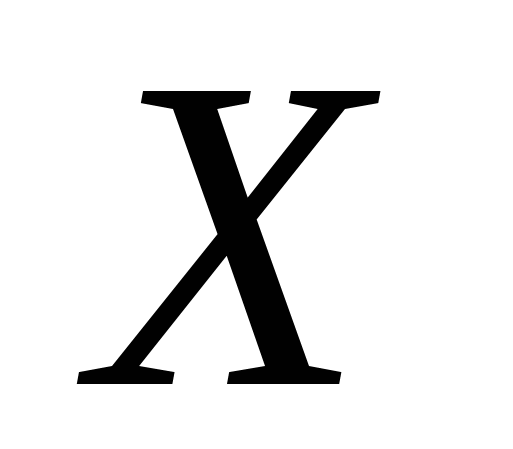
	-3	-1	0	2	4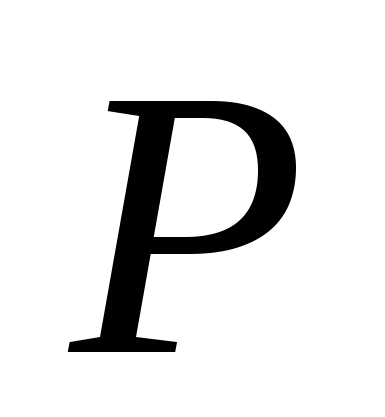
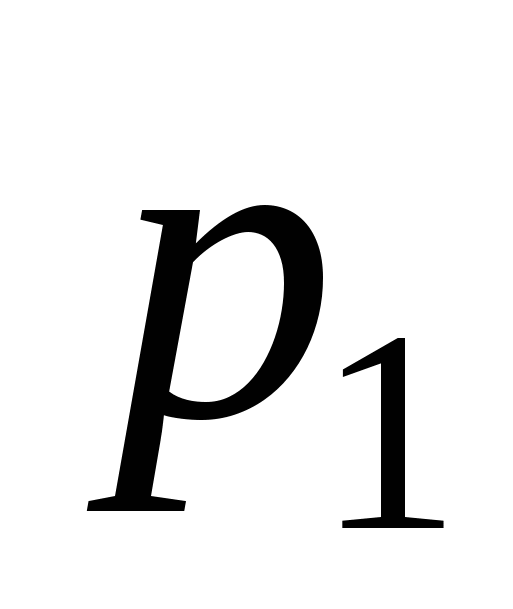
		0,2	0,15	0,25	0,2

Знайти: , ,, , , .

6. Неперервні випадкові величини.

Щільність розподілу випадкової величини має вигляд:

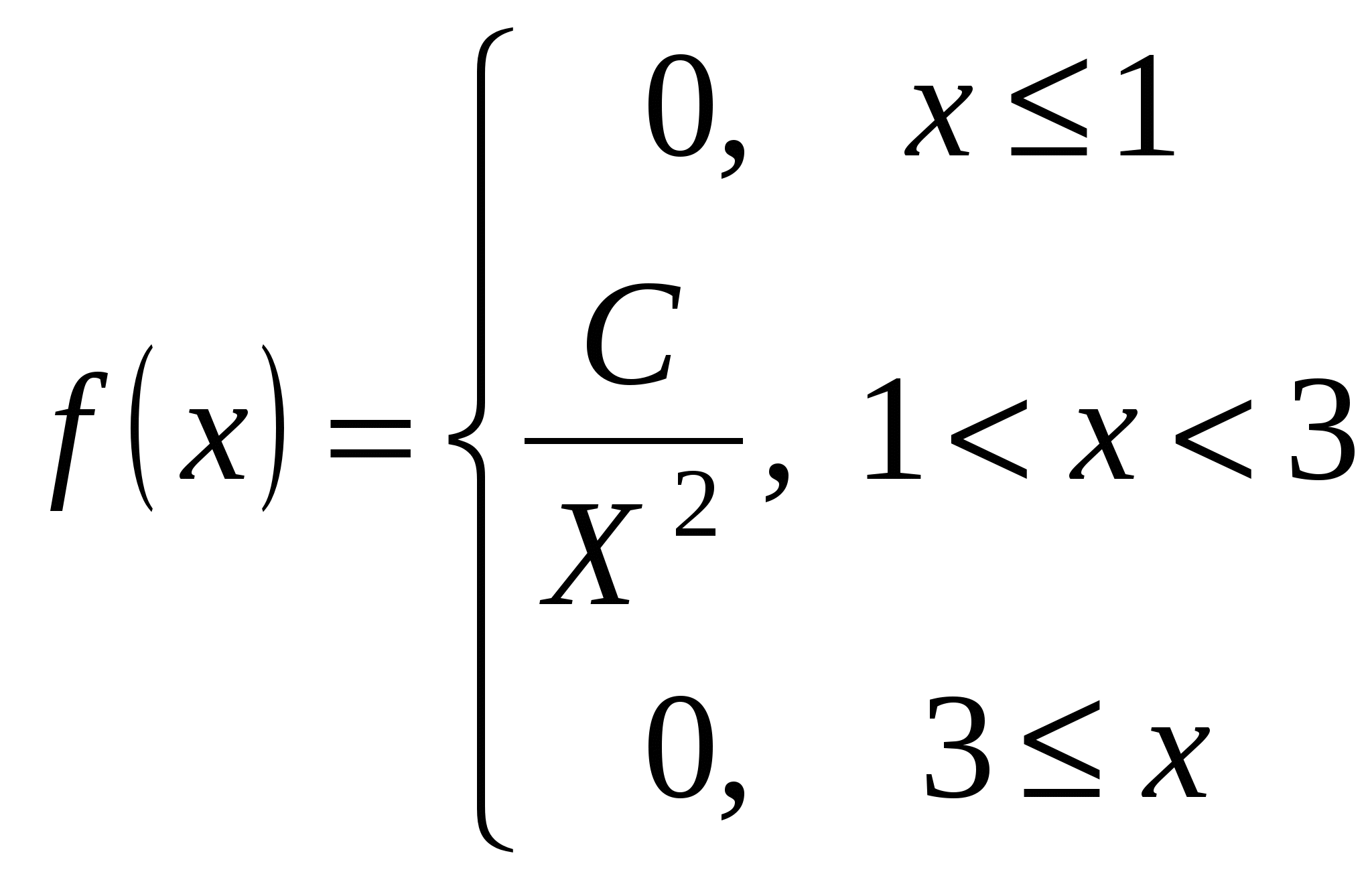
Знайти: параметр , ,, , .
7. Нормальний розподіл.

Випадкова величина 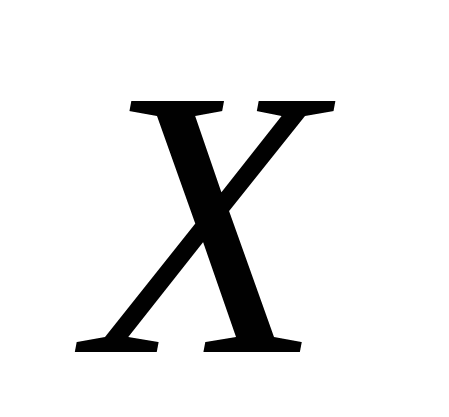має щільність розподілу:

Знайти: , , , , .

Затверджено навчально-методичною комісією кафедри ВМіЕ протокол №3 від 22.02.2000 р.

Донбаська державна академія будівництва та архітектури

Напрям: 0921 “Будівництво” Семестр IV

Навчальний предмет: “Вища математика”

Типовий розрахунок №8

ТЕОРІЯ ЙМОВІРНОСТЕЙ

Варіант 17.
1. Класичне визначення ймовірності.

В урні 3 білих, 3 червоних і 4 чорних кулі. Навмання виймають 3 з них. Знайти ймовірність події:

а) кулі різного кольору;

б) кулі одного кольору;

в) серед куль 2 чорних;

г) існує хоча б одна чорна.

2. Теореми додавання та множення.

Три мисливця одночасно стріляють в зайця. Ймовірність влучення для них відносно дорівнює 0,1; 0,4; 0,3. Знайти ймовірність того, що заєць вбитий, якщо для цього достатньо одного влучення.

3. Формула повної ймовірності і формула Байєса.
Робітник обслуговує 3 станка, на яких оброблюються однотипні деталі. Ймовірність браку для першого станка дорівнює 0,02, для другого – 0,03, для третього – 0,04. Оброблені деталі складаються в один ящик. Продуктивність першого станка в 3 рази більша, ніж другого, а третього - в 2 рази менша, ніж другого. Знайти ймовірність того, що взята навмання деталь буде бракованою.

4. Формула Бернуллі. Теорема Лапласа.

Подія відбудеться в досліді з ймовірністю 0,3. Знайти ймовірність подій.

а) в 6 дослідах відбудеться 2 події;

б) в 40 дослідах відбудеться 15 подій;

в) в 60 дослідах відбудеться більше 20 разів.

5. Дискретні випадкові величини.

Розподіл випадкової величини 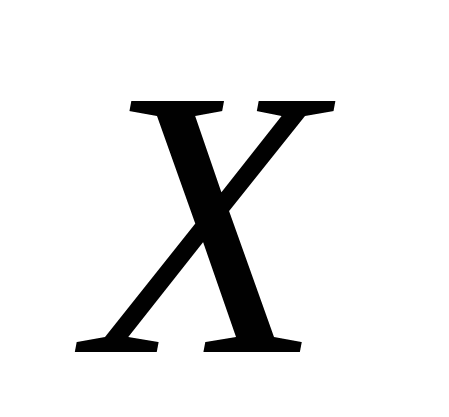має вигляд:

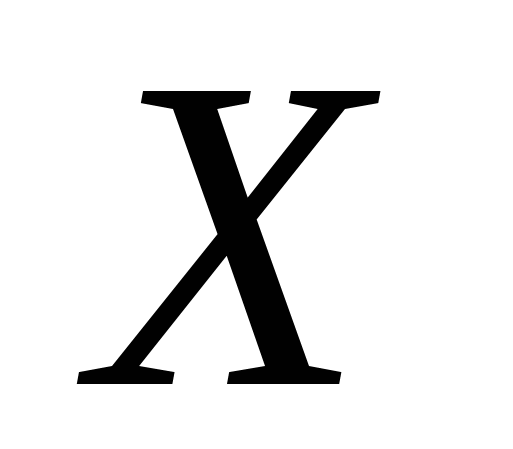
	2	3	8	10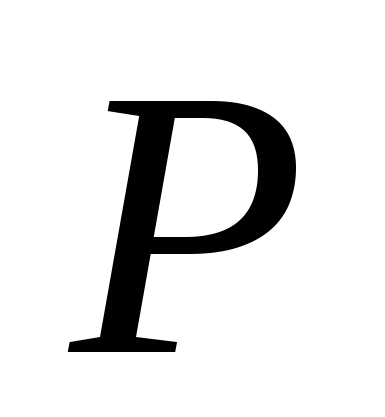
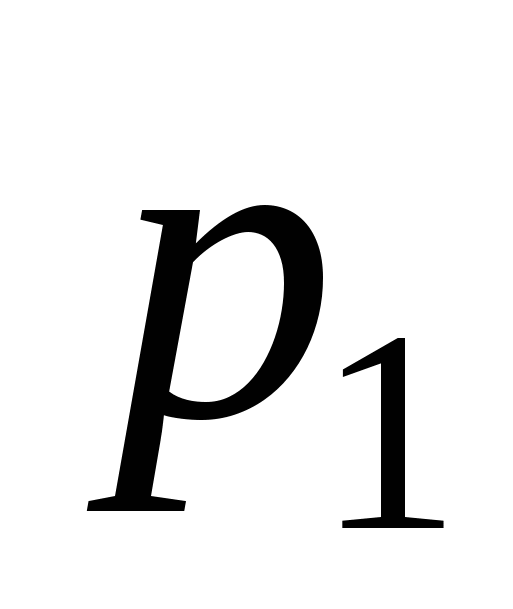
		0,2	0,1	0,4

Знайти: , , , , , .

6. Неперервні випадкові величини.

Щільність розподілу випадкової величини має вигляд:

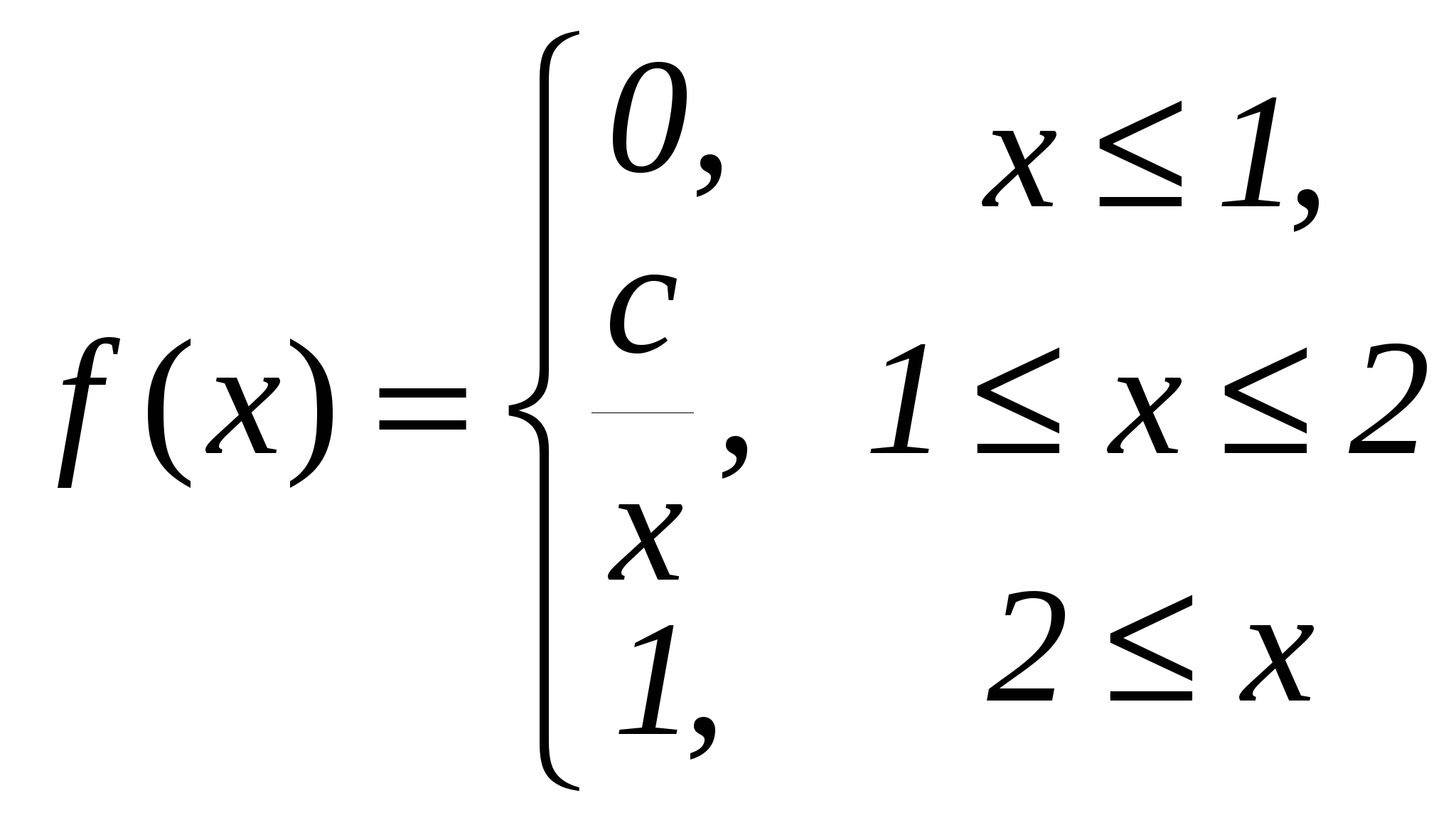
Знайти: параметр , ,, , .

7. Нормальний розподіл.

Щільність розподілу випадкової величини має вигляд:



Знайти: ,, , , .


Затверджено навчально-методичною комісією кафедри ВМіЕ протокол №3 від 22.02.2000 р.

Донбаська державна академія будівництва та архітектури

Напрям: 0921 “Будівництво” Семестр IV

Навчальний предмет: “Вища математика”

Типовий розрахунок №8

ТЕОРІЯ ЙМОВІРНОСТЕЙ

Варіант 18.
1. Класичне визначення ймовірності.

В коробці 12 куль: 4 білих, 6 червоних, 2 зелених. Виймають 3 з них. Знайти ймовірності:

а) всі кулі одного кольору;

б) всі кулі різного кольору;

в) вийняли 2 червоні кулі.

2. Теореми додавання та множення.

Три стрільці стріляють по цілі. Ймовірність попадання в ціль для першого дорівнює 0,75, для другого - 0,8, для третього - 0,9. Визначити ймовірності:

а) яка ймовірність того, що в ціль попадуть рівно 2 стрільці;

б) знайти ймовірність того, що в ціль попаде хоча б 1 стрілець;

3. Формула повної ймовірності і формула Байєса.

Виріб перевіряється на стандартність одним з двох контролерів. Ймовірність того, що виріб буде визнано стандартним першим контролером 0,9, а другим - 0,98. Знайти ймовірність того, що:

а) виріб при перевірці буде визнано стандартним;

б) виріб стандартний. Яка ймовірність того, що виріб перевірив другий контролер?

4. Формула Бернуллі. Теорема Лапласа.

Ймовірність, що покупець зробить покупку в магазині 0,3. Знайти ймовірності:

а) з 7 покупців покупку зроблять троє;

б) з 40 покупців покупку зроблять 14;

в) з 60 покупців покупку зроблять менше 20 покупців.

5. Дискретні випадкові величини.

Закон розподілу випадкової величини має вигляд:

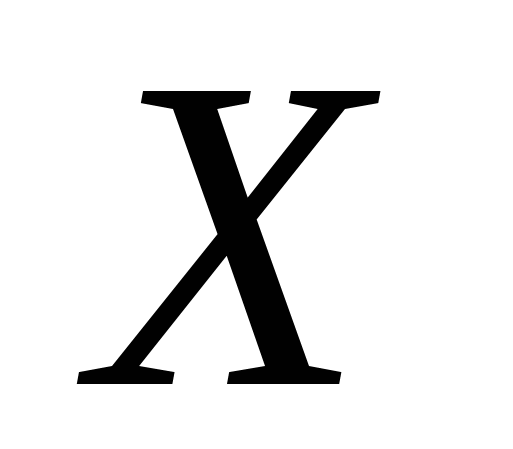
	-4	-1	0	4	9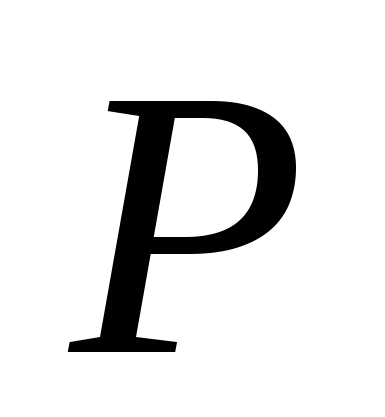
	0,2	0,1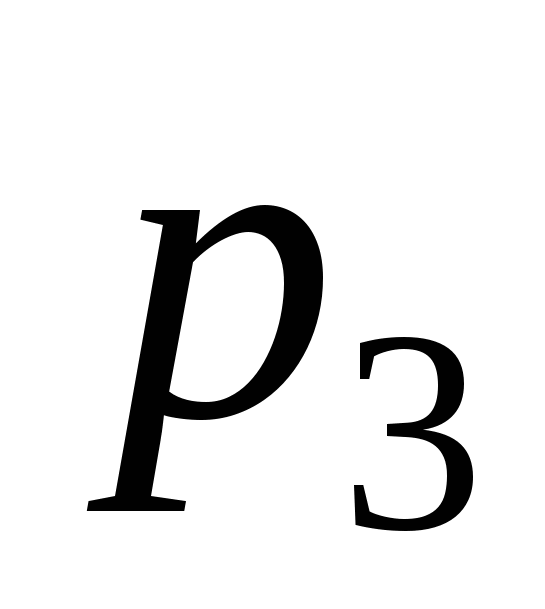		0,2	0,1

Знайти: , ,, , , , .

6. Неперервні випадкові величини.

Функція розподілу випадкової величини має вигляд:

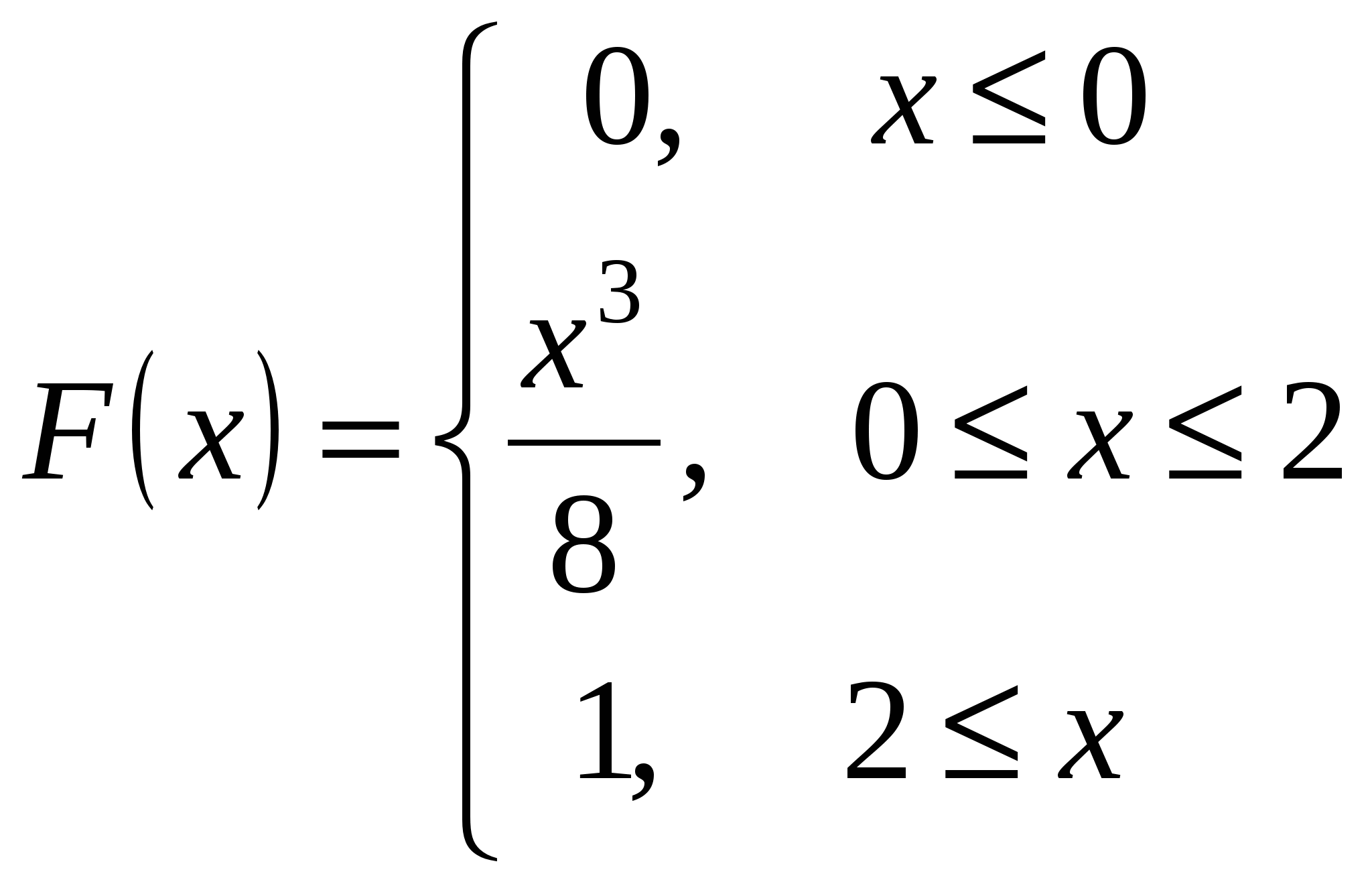
Знайти: ,, , .

7. Нормальний розподіл.

Випадкова величина має нормальний розподіл з щільністю:



Знайти: , , , .
Затверджено навчально-методичною комісією кафедри ВМіЕ протокол №3 від 22.02.2000 р.

Донбаська державна академія будівництва та архітектури

Напрям: 0921 “Будівництво” Семестр IV

Навчальний предмет: “Вища математика”

Типовий розрахунок №8

ТЕОРІЯ ЙМОВІРНОСТЕЙ

Варіант 19.
1. Класичне визначення ймовірності.

З партії, в якій 31 деталь без дефектів і 6 з дефектами, беруть навмання 3 деталі.

Чому дорівнює ймовірність в наступних випадках:

а) всі три деталі без дефектів;

б) хоча б одна деталь без дефекту.

2. Теореми додавання та множення.

Перший стрілець влучить в ціль з ймовірністю 0,7, другий - 0,8, третій - 0,75. Визначити ймовірності:

а) всі стрільці влучать в ціль?

б) тільки один влучить в ціль?

в) хоча б один влучне в ціль.

3. Формула повної ймовірності і формула Байєса.

Відомо, що з 100 деталей 60 виготовлені першим заводом, 40 - другим. На першому заводі 5% виробів браковані, на другому - 3% :

а) знайти ймовірність того, що навмання вийнята деталь виявиться бракованою;

б) вийнята бракована деталь. Яка ймовірність того, що вона виготовлена 1-м заводом?

4. Формула Бернуллі. Теорема Лапласа.

Де-хто кидає гральний кубик. Знайти ймовірність:

а) при 7 кидках рівно 2 рази випаде 6 очок;

б) при 40 кидках 6 очок випаде 15 разів;

в) при 70 кидках 6 очок випаде не менше 10 разів.

5. Дискретні випадкові величини.

Закон розподілу дискретної випадкової величини має вигляд:

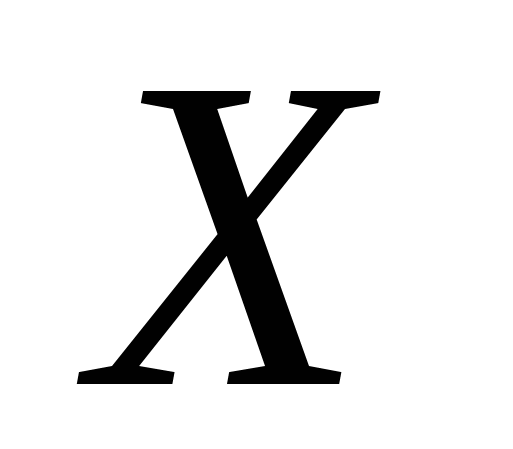
	1	5	9	13	18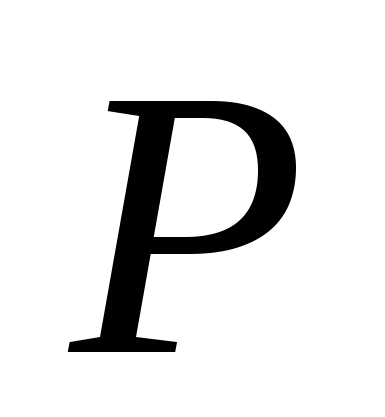
	0,1	0,36	0,35	0,14

Знайти: , ,, , , , .
6. Неперервні випадкові величини.

Щільність розподілу випадкової величини має вигляд:

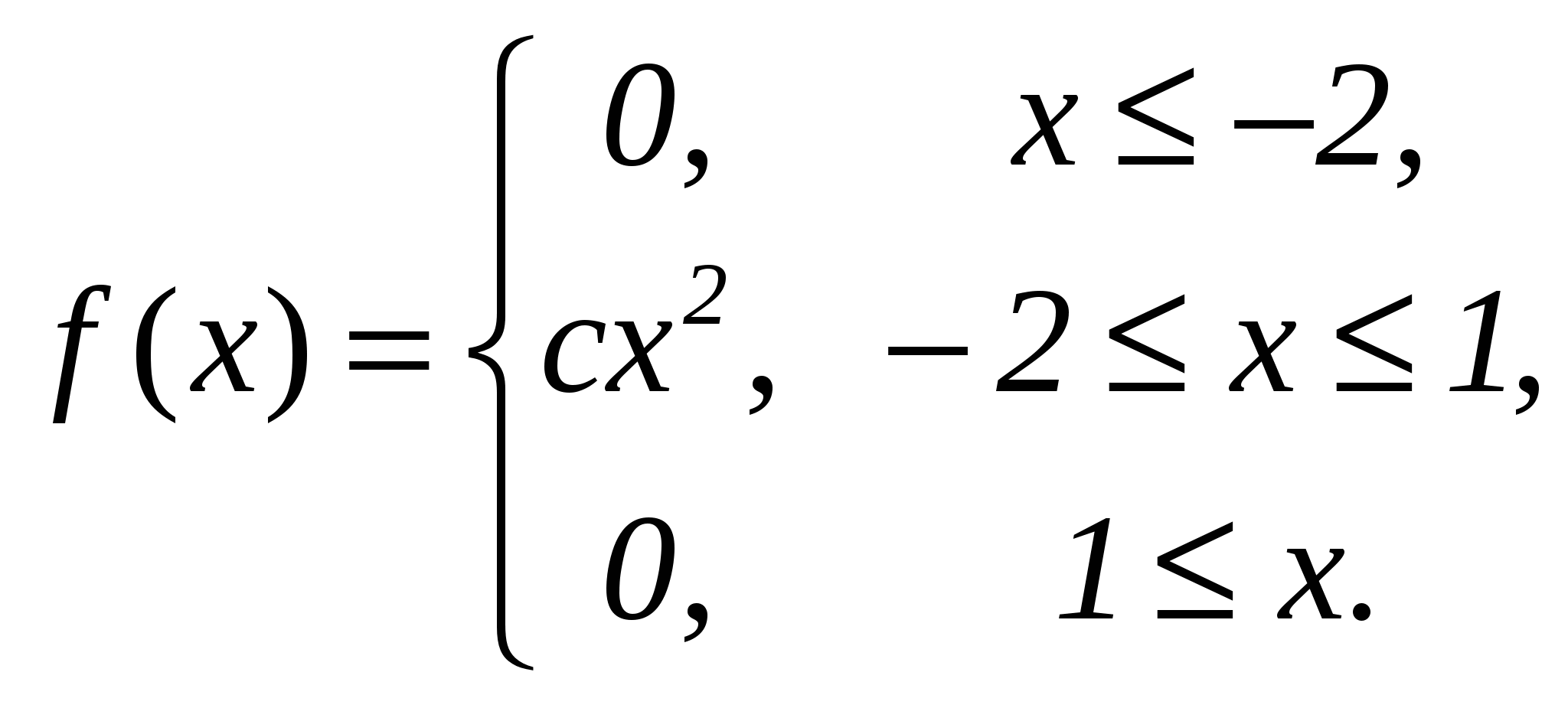
Знайти: параметр , , , .

7. Нормальний розподіл.
Довжина виробу виявляється випадковою величиною з середнім значенням мм і середнім квадратичним відхиленням мм.

Знайти ймовірності:

а) довжина виробу більш 1480 мм і менше 1510 мм;

б) довжина виробу відрізняється від середнього не більше, ніж на 5 мм.

Затверджено навчально-методичною комісією кафедри ВМіЕ протокол №3 від 22.02.2000 р.

Донбаська державна академія будівництва та архітектури

Напрям: 0921 “Будівництво” Семестр IV

Навчальний предмет: “Вища математика”

Типовий розрахунок №8

ТЕОРІЯ ЙМОВІРНОСТЕЙ

Варіант 20.
1. Класичне визначення ймовірності.

В студентський групі вчиться 14 чоловік: 8 хлопців і 6 дівчат. На профспілкову конференцію вибирають делегацію з 5 чоловік. Знайти ймовірності:

а) серед делегатів буде 3 хлопці і 2 дівчини.

б) серед делегатів будуть тільки хлопці;

в) серед делегатів буде хоча б один хлопець.

2. Теореми додавання та множення.

Бензин є на першій бензоколонці з ймовірністю 0,6; на другій з ймовірністю 0,3; на третій – 0,7. Знайти ймовірності:

а) бензин є рівно на двох колонках;

б) бензин відсутній на всіх колонках;

в) бензин є хоча б на одній колонці.

3. Формула повної ймовірності і формула Байєса.
На складання потрапляють деталі з 3-х автоматів. Відомо, що перший автомат дає 0,3% браку, другий - 0,2% браку, третій - 0,4%. З першого автомату надійшло 1000, з другого - 2000 і з третього   2500 деталей. Знайти ймовірності:

а) на складання потрапила бракована деталь;

б) відомо, що на складання потрапила бракована деталь. Знайти ймовірність, що вона потрапила з другого автомату.

4. Формула Бернуллі. Теорема Лапласа.

Двадцять відсотків всіх чоловіків носить взуття 43 розміру. Знайти ймовірності:

а) серед 7 чоловіків 2 носять взуття 43 розміру;

б) серед 60 рівно 20 носять взуття 43 розміру;

в) не менше 15 серед 80 носять взуття 43 розміру.

5. Дискретні випадкові величини.

Випадкова величина 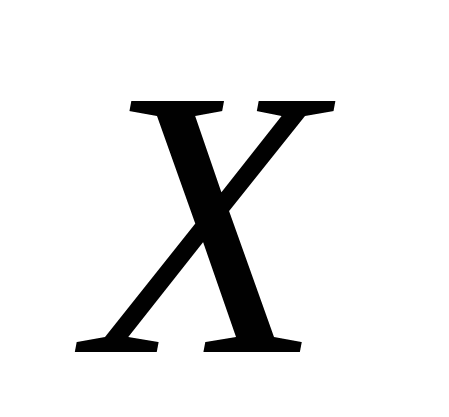має розподіл:

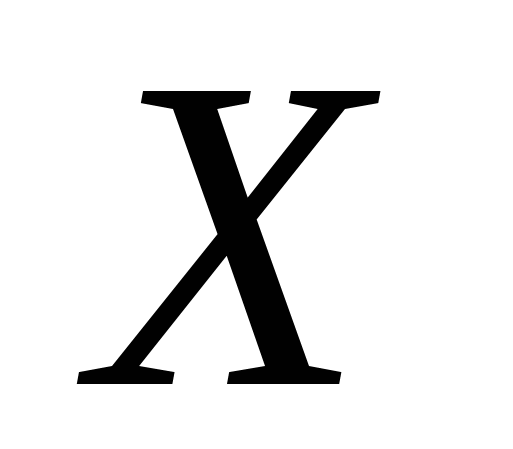
	-3	0	1	3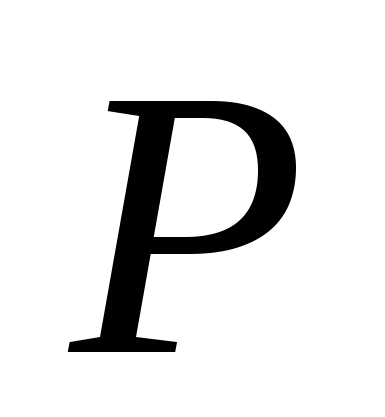
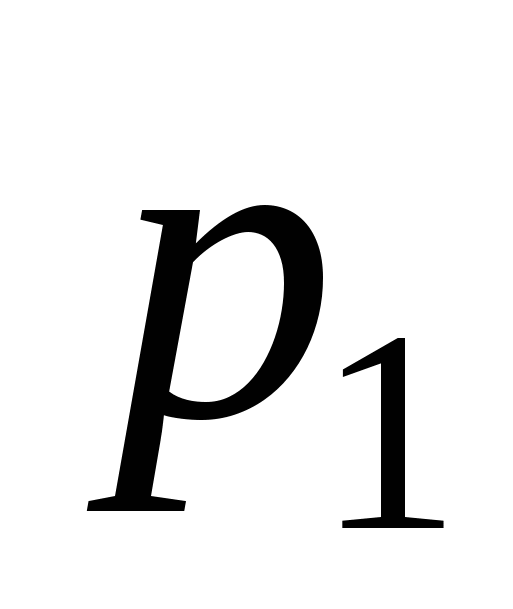
		0,2	0,1	0,3

Знайти: , , , , , .

6. Неперервні випадкові величини.

Випадкова величина 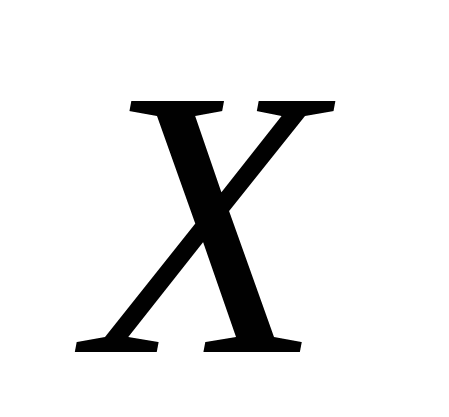має щільність розподілу:

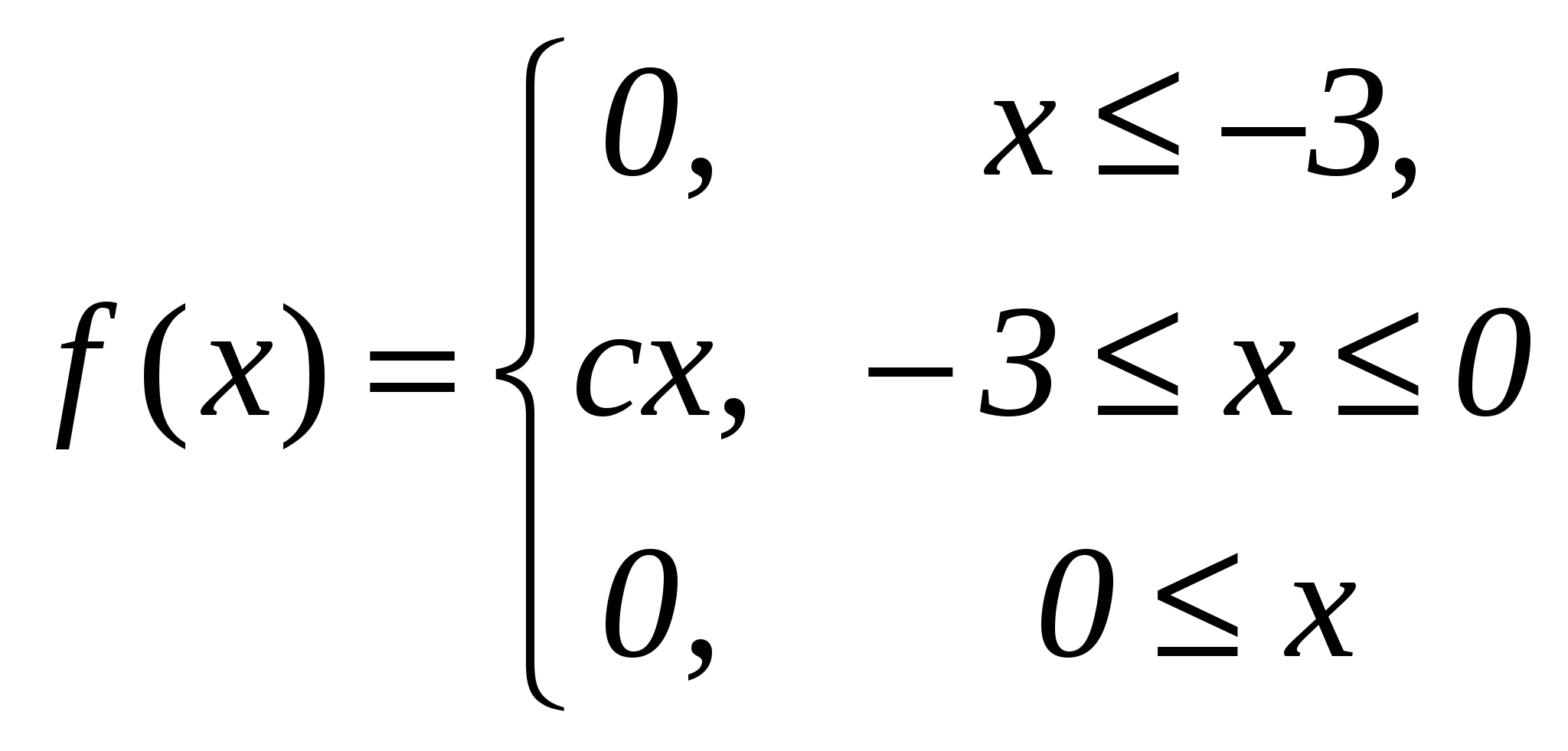
Знайти: параметр , ,, , .

7. Нормальний розподіл.

Випадкова величина має нормальний розподіл з параметрами =, = .

Знайти:

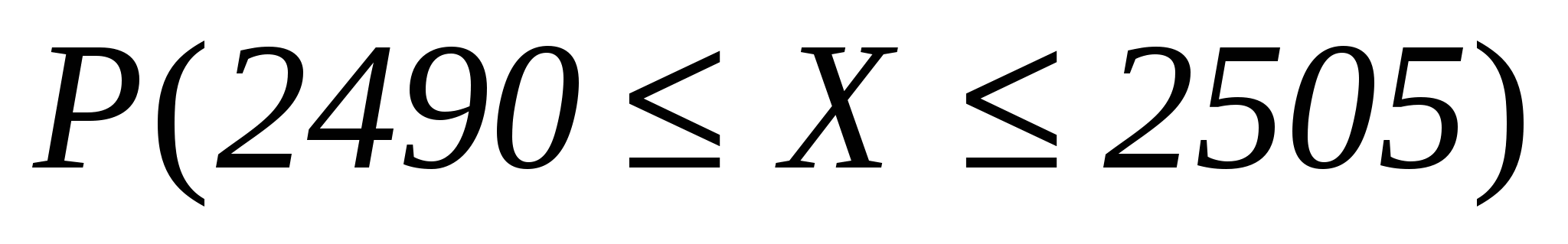а) ; б) .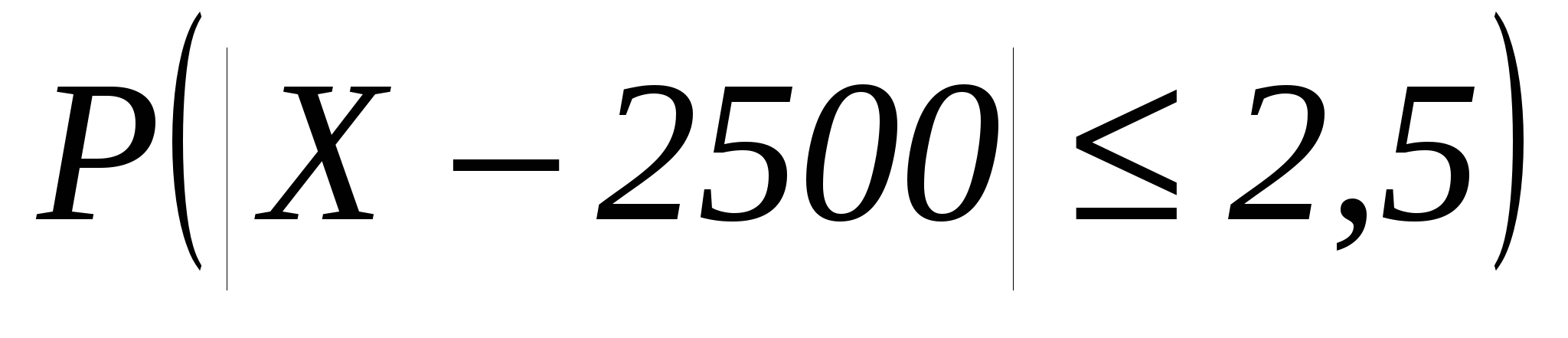

Затверджено навчально-методичною комісією кафедри ВМіЕ протокол №3 від 22.02.2000 р.