Руководитель проекта А. Н. Надольский 2021 г. Пояснительная записка к курсовой работе по дисциплине Теоретические основы радиоэлектроники Тема Расчет спектральных характеристик радиотехнических сигналов Проверил
 Скачать 450.04 Kb. Скачать 450.04 Kb.
|
1.2.3 Модулированные колебанияМодулированные сигналы – это гармонические колебания высокой частоты, один или несколько параметров которых изменяются по закону несущего колебания. Такие сигналы называют ещё радиосигналами. Амплитудная модуляция: s(t) = U(t)cos( 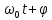 ) ) Угловая модуляция: s(t) = Ucos( 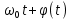 ) ) 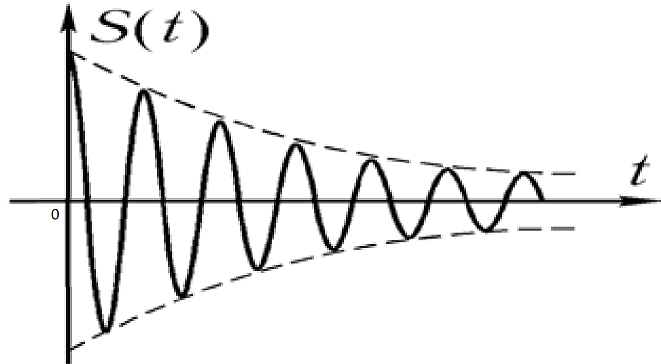 Рисунок 1.6 Модулированное колебание Также в радиоэлектронике часто пользуются такими сигналами как: - дельта-функция Рисунок 1.6 Модулированное колебание Также в радиоэлектронике часто пользуются такими сигналами как: - дельта-функция - функция единичного скачка (функция Хевисайда). 1.2.4 Дельта-функция Дельта-функция - функция единичного скачка (функция Хевисайда). 1.2.4 Дельта-функция Дельта-функция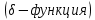 – это математическая модель не существующего сигнала, который имеет бесконечную по величине амплитуду и нулевую длительность (рис. 1.7). – это математическая модель не существующего сигнала, который имеет бесконечную по величине амплитуду и нулевую длительность (рис. 1.7). 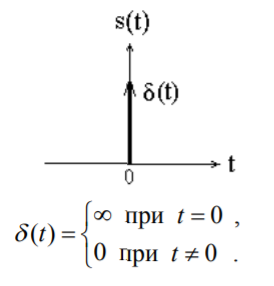 Рисунок 1.7 – Дельта функция Рисунок 1.7 – Дельта функция Свойства δ- функции: 1. Площадь сигнала, описываемого δ- функцией, равна 1, т.е. 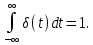 2. Селектирующее свойство: 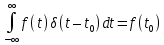 , где f(t)- произвольная функция. , где f(t)- произвольная функция.δ- функция относится к числу испытательных сигналов, т.к. реакция устройства на сигнал, описывающий δ- функцию, есть импульсная характеристика устройства. 1.2.5 Функция единичного скачка Функция единичного скачка (функция Хевисайда) описывает процесс резкого перехода физического устройства из одного состояния в другое. На рис 1.8 приведен график этой функции. 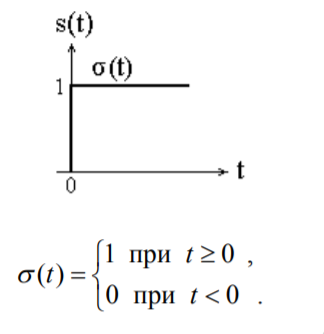 Рисунок 1.8 – Функция единичного скачка 1.2.6Основные характеристики сигналов Для сигнала, существующего в интервале Рисунок 1.8 – Функция единичного скачка 1.2.6Основные характеристики сигналов Для сигнала, существующего в интервале 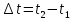 ,наиболее важными являются следующие характеристики (предполагаем, что сигнал представлен в комплексной форме): 1.Среднее значение сигнала ,наиболее важными являются следующие характеристики (предполагаем, что сигнал представлен в комплексной форме): 1.Среднее значение сигнала 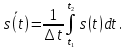 Среднее значение сигнала – это по существу его постоянная составляющая. 2.Мгновенная мощность сигнала Среднее значение сигнала – это по существу его постоянная составляющая. 2.Мгновенная мощность сигнала 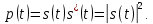 3.Энергия сигнала 3.Энергия сигнала 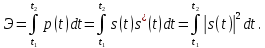 4.Средняя мощность сигнала 4.Средняя мощность сигнала 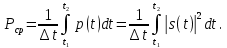 Для периодического сигнала ,энергия которого равна бесконечности, среднее значение и энергетические характеристики определяются в пределах одного периода: 1.Среднее значение сигнала Для периодического сигнала ,энергия которого равна бесконечности, среднее значение и энергетические характеристики определяются в пределах одного периода: 1.Среднее значение сигнала 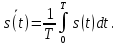 2.Мгновенная мощность сигнала 2.Мгновенная мощность сигнала 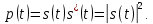 3.Энергия сигнала 3.Энергия сигнала 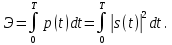 4.Средняя мощность сигнала 4.Средняя мощность сигнала 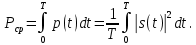 В этом разделе мы рассмотрели классификацию и виды радиотехничес- ких сигналов, также основные характеристики сигналов. В этом разделе мы рассмотрели классификацию и виды радиотехничес- ких сигналов, также основные характеристики сигналов. 2 СПЕКТРАЛЬНЫЙ АНАЛИЗ РАДИОТЕХНИЧЕСКИХ СИГНАЛОВ 2.1 Спектральный анализ непериодических сигналов 2.1.1 Спектральные характеристики непериодических сигналов В радиотехнике в качестве непериодических сигналов рассматривают обычно одиночные импульсные сигналы. Для спектрального анализа таких сигналов используются преобразования Фурье [1]: 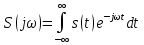 ; ; 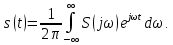 (1.1) (1.1)2.1.2 Амплитудный и фазовый спектры непериодического сигнала Для спектральной плотности сигнала справедливы все свойства комплексных чисел. Выполним некоторые преобразования. 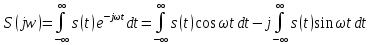 , ,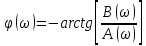 - фазовый спектр сигнала; - фазовый спектр сигнала;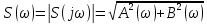 – амплитудный спектр сигнала; – амплитудный спектр сигнала;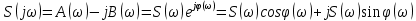 , ,где 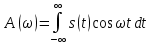 –действительная часть спектра; –действительная часть спектра;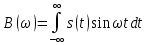 – мнимая часть спектра; – мнимая часть спектра;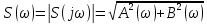 – амплитудный спектр сигнала; – амплитудный спектр сигнала;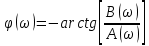 - фазовый спектр сигнала; - фазовый спектр сигнала;Как видно из полученных выражений, 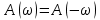 и и 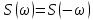 , ,т.е. действительная часть спектра и амплитудный спектр-функции четные; 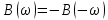 и и 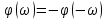 , ,т.е. мнимая часть спектра и фазовый спектр –функции нечетные. При 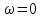 выражение (1.1.1) приобретает вид. выражение (1.1.1) приобретает вид.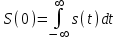 . .Отсюда можно сделать вывод, что спектральная плотность любого сигнала на нулевой частоте равна площади под кривой графика сигнала. Учитывая, что амплитудный спектр 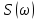 -функция четная, следовательно можно записать -функция четная, следовательно можно записатьВ тригонометрической форме можно представить также формулу (1.1.2): 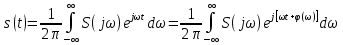 , ,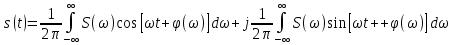 . .Учитывая, что амплитудный спектр 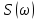 - функция четная, следовательно можно записать: - функция четная, следовательно можно записать: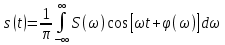 . .Полученные выражения используются для расчета соответствующих характеристик сигнала. 2.1.3 Спектральная плотность четного и нечетного сигналов Пусть 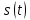 – четный сигнал, т.е. – четный сигнал, т.е. 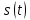 = =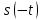 ,тогда ,тогда 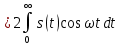 . .Следовательно, спектральная плотность четного сигнала содержит только действительную часть, подынтегральная функция которой также четная. Пусть 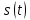 – нечетный сигнал, т.е. – нечетный сигнал, т.е. 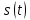 = =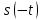 ,тогда ,тогда 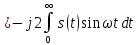 . .Следовательно, спектральная плотность нечетного сигнала содержит только мнимую часть, подынтегральная функция которой четная. 2.2 Спектральный анализ периодических сигналов 2.2.1 Спектральные характеристики периодических сигналов Гармонический спектральный анализ периодических сигналов предполагает разложение сигнала в ряд Фурье по тригонометрическим функциям – синусам и косинусам. Эти функции описывают гармонические колебания , которые сохраняют свою форму в процессе преобразований линейными устройствами (изменяются только амплитуда и фаза), что позволяет использовать теорию колебательных систем для анализа свойств радиотехнических цепей. Ряд Фурье можно представить так 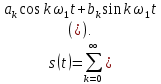 Для того чтобы коэффициенты 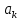 определялись по одной и той же формуле для определялись по одной и той же формуле для 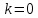 и и 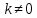 , ряд Фурье принято записывать следующим образом: , ряд Фурье принято записывать следующим образом: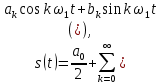 (2.1) (2.1) где 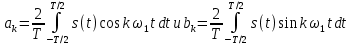 . (2.2) . (2.2)Полученные результаты позволяют сделать следующие выводы: 1.Периодический сигнал можно представить в виде суммы бесконечного числа гармонических составляющих (синусоидальных и косинусоидальных) каждая из которых характеризуется своей амплитудой и частотой. Совокупность этих составляющих называют спектром сигнала, а совокупность их амплитуд – амплитудным спектром сигнала. 2.Составляющая 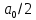 – это “нулевая ” (постоянная) составляющая с частотой , равной 0. – это “нулевая ” (постоянная) составляющая с частотой , равной 0.3.Амплитуды составляющих определяются по формулам (2.2). 4.Частоты составляющих дискретны ,т.e. имеют значения , кратные основной частоте - частоте сигнала:0, 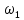 , ,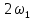 , ,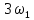 ,… .Таким образом, спектр периодического сигнала является дискретным. ,… .Таким образом, спектр периодического сигнала является дискретным.Определение спектров периодических сигналов сводится по существу к нахождению коэффициентов ряда Фурье. Решение этой задачи иногда значительно упрощается , если учитываются особенности сигналов. Наиболее часто пользуются, другой более компактной формой записи ряда Фурье, называемой комплексной формой. 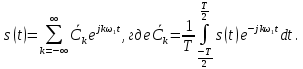 2.2.2 Амплитудный и фазовый спектры периодических сигналов Практическое применение имеет другая форма записи тригонометрического ряда Фурье. Известно, что 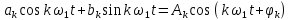 , ,где 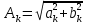 и и 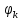 = =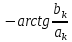 . .Тогда ряд (2.1) можно записать так: 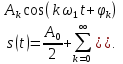 Таким образом, периодический сигнал любой формы представляется постоянной составляющей 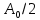 и бесконечной совокупностью гармонических составляющих с амплитудами и бесконечной совокупностью гармонических составляющих с амплитудами 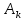 и начальными фазами и начальными фазами 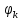 . .Совокупность составляющих 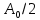 и амплитуд и амплитуд 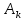 называют амплитудным спектром , а совокупность фаз называют амплитудным спектром , а совокупность фаз 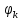 – фазовым спектром сигнала. – фазовым спектром сигнала.Для комплексного ряда Фурье: 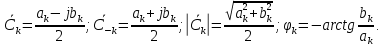 Для комплексной формы - спектр амплитуд 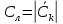 и спектр фаз и спектр фаз 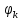 . . 2.2.3 Спектры четных и нечетных сигналов Определение спектров периодических сигналов сводится по существу к нахождению коэффициентов ряда Фурье. Решение этой задачи иногда значительно упрощается , если учитываются особенности сигналов. Спектр четных сигналов Если сигнал 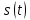 четный , то коэффициенты четный , то коэффициенты 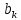 равны 0, т.к. подынтегральная функция равны 0, т.к. подынтегральная функция 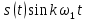 является нечетной (интеграл от нечетной функции по симметричному промежутку равен 0). При этом ряд Фурье содержит только косинусы и постоянную составляющую, т.е. является нечетной (интеграл от нечетной функции по симметричному промежутку равен 0). При этом ряд Фурье содержит только косинусы и постоянную составляющую, т.е. 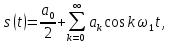 где коэффициенты 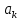 равны: равны: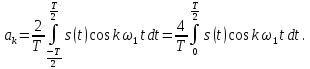 Таким образом, для определения коэффициентов ряда Фурье четных сигналов достаточно иметь сигнал , заданный на половине периода. Спектр нечетных сигналов Если сигнал 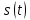 нечетный , то коэффициенты нечетный , то коэффициенты 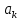 равны 0, т.к. подынтегральная функция равны 0, т.к. подынтегральная функция 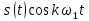 является нечетной. При этом ряд Фурье содержит только синусы является нечетной. При этом ряд Фурье содержит только синусы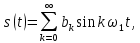 где коэффициенты 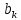 равны равны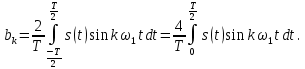 В данном случае также для определения коэффициентов Фурье достаточно иметь сигнал заданный на половине периода. В этом разделе мы рассмотрели спектральный анализ радиотехнических сигналов. В дальнейшем будем использовать формулы полученные в данном разделе для нахождения спектральных характеристик сигнала заданного в курсовом проекте. 3 СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬЕ Формулы прямого и обратного преобразования Фурье позволяют по сигналу s(t) определить его спектральную плотность S( 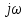 ) и, если в этом есть необходимость, по известной спектральной плотности S( ) и, если в этом есть необходимость, по известной спектральной плотности S(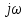 ) определить сигнал s(t). Соответствие между сигналом и его спектром принято записывать следующим образом: ) определить сигнал s(t). Соответствие между сигналом и его спектром принято записывать следующим образом:s(t)↔ S( 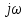 ). ).С помощью свойств преобразований Фурье можно определить спектр измененного сигнала, преобразуя спектр первоначального сигнала. Основные свойства: 1. Линейность: s1(t)↔ S1( 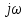 ) )⁞ ⁞ (3.1) sn(t)↔ Sn( 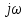 ) )___________________________ 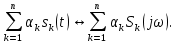 Вывод: прямое преобразование Фурье является линейной операцией, обладает свойствами однородности и аддитивности. Поэтому спектр суммы сигналов равен сумме спектров. 2. Спектр сигнала, сдвинутого во времени: s(t)↔ S( 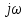 ) )_____________________ (3.2) 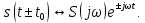 Вывод: сдвиг сигнала во времени на величину ±t0 приводит к изменению фазового спектра на величину ± 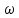 t0. Амплитудный спектр не изменяется. t0. Амплитудный спектр не изменяется.3. Изменение масштаба во времени: s(t)↔ S( 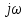 ) )___________________ (3.3) 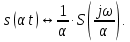 Вывод: при сжатии (расширении) сигнала во времени в определенное число во столько же раз расширяется (сжимается) его спектр, т.е. длительность сигнала и ширина спектра находятся в обратной пропорциональности между собой. 4. Спектр производной от сигнала: s(t)↔ S( 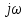 ) )_____________________ (3.4) ds(t)/dt↔ 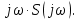 Вывод: спектр производной сигнала равен спектру исходного сигнала, умноженному на 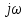 . При этом амплитудный спектр изменяется пропорционально изменению частоты ω, а к фазовой характеристике исходного сигнала добавляется постоянная составляющая, равная π/2. . При этом амплитудный спектр изменяется пропорционально изменению частоты ω, а к фазовой характеристике исходного сигнала добавляется постоянная составляющая, равная π/2.5. Спектр интеграла от сигнала: s(t)↔ S( 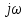 ) )______________________ (3.5) 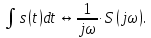 Вывод: спектр сигнала, равного интегралу от исходного сигнала, равен спектру исходного сигнала, деленному на 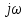 . При этом амплитудный спектр изменяется обратно пропорционально изменению частоты . При этом амплитудный спектр изменяется обратно пропорционально изменению частоты 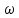 , т.е. амплитудный спектр равен S( , т.е. амплитудный спектр равен S(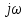 )/ )/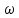 , а к фазовой характеристике исходного сигнала добавляется постоянная составляющая, равная -π/2. , а к фазовой характеристике исходного сигнала добавляется постоянная составляющая, равная -π/2.6. Спектр радиоимпульса: sв(t)↔ Sв( 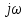 ) )___________________________________________ (3.6) sв(t)cos 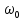 t↔ t↔ 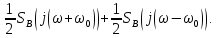 Вывод: обратим внимание, что спектр видеоимпульса отображается в области низких частот – низкочастотный сигнал, а спектр радиоимпульса – высоких частот – высокочастотный сигнал. 7. Спектр произведения двух сигналов: s1(t)↔ S1( 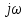 ) )s2(t)↔ S2( 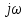 ) )_____________________________ (3.7) s1(t)s2(t)↔ 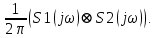 Вывод: Спектр произведения двух сигналов равен свертке их спектров, умноженной на коэффициент 1/(2π). В данном разделе мы рассмотрели свойства преобразования Фурье. Данные свойства в дальнейшем будут использоваться для расчета спектральных характеристик сигнала 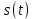 , заданным в курсовом проекте. , заданным в курсовом проекте. |
