Руководство по боевой работе подразделений оптической разведки артиллерии 2001
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
Прямая засечка42. Определение координат НП прямой засечкой (рис. 5) заключается в измерении углов на двух контурных точках или пунктах геодезической сети и НП. Угол засечки (угол при точке НП) должен быть от 5-00 до 25-00. Порядок вычисления прямой засечки изложен в Приложении 5. В том случае, если измерены все три угла (на двух исходных точках и на НП), угловая невязка треугольника не должна превышать 0-03. Обратная засечка43. Обратной засечкой называется способ определения координат точки, когда измерения производятся на привязываемой точке. Различают следующие разновидности обратной засечки: по измеренным углам; по дирекционным углам (ориентированным прибором); по измеренным углу и расстояниям; по измеренным расстояниям. 44. При засечке по измеренным углам координаты привязываемой точки определяют по углам между направлениями на четыре исходных пункта (точки) (рис.6).  Р (НП) Хр=16599 Ур=24400  α=11-46 β=11-92       А ХА=14600 УА=23400 В ХВ=14460 УВ=24900 Рис. 5. Определение координат НП прямой засечкой  С ХC=27320 УC=77752          D ХD=26738 УD=77355  β=6-66 А ХА=27180 УА=74727  =7-68 =3-67     P Хр=27079 Ур=76004 Рис. 6. Определение координат НП обратной засечкой по измеренным углам Пункты (точки) А, В, С являются исходными для вычислений координат точки Р, а пункт D - контрольным. При выборе исходных пунктов (точек) А, В и С необходимо учитывать, что задача решается надежно, если привязываемая точка Р (рис. 6) находится : внутри треугольника АВС; вне треугольника против одной из его вершин; против одной из сторон треугольника. Задача не решается, если привязываемая точка Р находится на окружности, проходящей через пункты (точки) А, В и С. Если точка Р находится вблизи окружности, то задача решается, но точность засечки резко снижается. 45. Обратная засечка по измеренным углам при использовании контурных точек в качестве исходных может решаться графическим или смешанным методом по карте. Графически обратная засечка решается способом Болотова. Для этого на листе кальки накалывают точку Р (НП) и из нее прочерчивают прямую линию, от которой последовательно строят углы , и . Прочерченные направления обозначают названиями местных предметов или: левое - А, затем - В, С и D. После этого кальку накладывают на карту (аэроснимок) и, поворачивая ее, совмещают направления на кальке с соответствующими точками карты (аэроснимка). После совмещения всех направлений перекалывают точку Р с кальки на карту (рис. 6). При смешанном методе после измерения углов и между направлениями с НП (точка Р) на контурные точки А, В и С с известными координатами (рис. 7) на карте измеряют расстояние между исходными точками АВ и ВС и рассчитывают вспомогательные величины: R1= Пример (рис. 7). Определить величины R1 и R2. Решение. Переводят значения и из делений угломера в доли градуса: =7-68, 0=46,08о, =6-66, о=39,96о. Рассчитывают величины R1 и R2: R1 = Раствором циркуля, равным величине R1, из точек А и В делают засечку вспомогательной точки О1 и, не меняя раствора циркуля, из точки О1 проводят дугу в районе определяемой точки. Аналогично раствором циркуля, равным R2, из точек В и С делают засечку точки О2, из которой проводят вторую дугу. Пересечение дуг, проведенных радиусами R1 и R2 из точек О1 и О2, является искомой точкой Р. 46. При засечке по дирекционным углам (обратная засечка ориентированным прибором) вместо измерения углов , и с привязываемой точки Р (рис. 8) определяют дирекционные углы. 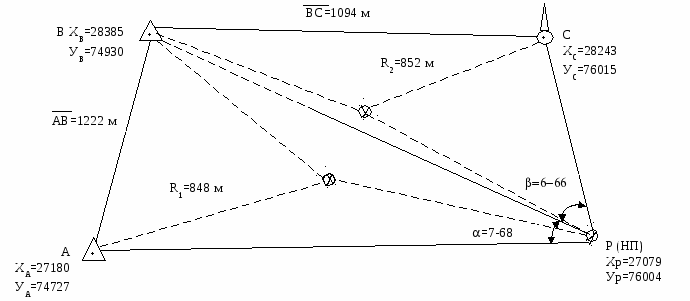  Рис. 7. Определение координат НП решением обратной засечки смешанным методом (вариант)    AP=26-48        А ХА=27180 УА=74728  BP=26-79   В Хв=25738 Ув=75355 С Хс=24321 Ус=76753      CP=39-91   Р Хр=23879 Ур=76004 Рис. 8. Определение координат НП обратной засечкой по обратным дирекционным углам При использовании контурных точек в качестве исходных координаты НП можно определять графическим или смешанным методом по карте, при этом: изменяют каждый дирекционный угол на 30-00, получая обратные дирекционные углы AP, BP и CP (рис. 8); на карте (аэроснимке) или на ПУО, на котором предварительно нанесены исходные точки, прочерчивают направления с исходных точек на НП по дирекционным углам AP, BP и CP и на пересечении этих направлений получают положение НП. Обратная засечка считается выполненной правильно, если наибольшая сторона треугольника погрешностей не превышает 3 мм. За место положения НП принимают центр треугольника погрешностей. 47. Обратной засечкой по измеренным углу и расстояниям называется способ определения координат привязываемой точки Р по измеренным на этой точке углу Р () между направлениями на два исходных пункта А и В и расстояниям до этих пунктов РА и РВ (рис. 9). Обратную засечку вычисляют в следующем порядке: а) Из решения треугольника АВР по измеренным сторонам АР и ВР и углу Р () определяют углы А, В и сторону АВ. б) Определяют сторону АВ и дирекционный угол (АВ) решением обратной геодезической задачи по координатам пунктов (точек) А и В. Для контроля сравнивают значения стороны АВ, найденные из решения треугольника АВР и из решения обратной геодезической задачи. Разность значений AB не должна превышать 20 м. в) Определяют дирекционные углы (АР) и (ВР) по формулам: (AP) = (AB) + ; (BP) = (BA) - . г) Дважды вычисляют координаты привязываемой точки решением прямых геодезических задач, используя в качестве исходных точек пункты А и В, при этом разность координат точки Р не должна превышать 20 м. За окончательные координаты привязываемой точки принимают их средние значения. При работе ориентированным прибором определяют дирекционные углы (АР) и (РВ), угол Р вычисляют как разность дирекционных углов (ВР) и (АР). Пример (рис. 9). При геодезической привязке НП измерен угол между направлениями на контурные точки А и В и расстояний до них, РА (1) и РВ (2) соответственно. Дано: =2-49, РА=3468 м, РВ=7128 м. Вычислить координаты НП. Решение. Значения угла переводят в градусную меру: =2-49 . 6о=14,942о. Решением треугольника АВР определяют углы А, В и сторону АВ: А=К1+К2=82,529о+69,210о=151,739о=25-30; В=К1-К2=82,529о-69,210о=13,319о=2-21; Определяют величину стороны АВ=3882-3882=0 м, что удовлетворяет условию АВ20 м. Определяют дирекционные углы (АР) и (ВР): (АР)=(АВ)+А=12,722о+151,739о=164,461о=27-41; (ВР)=(ВА)-В=192,722о-13,319о=179,403о=29-90. Определяют координаты НП (точки Р) решением прямой геодезической задачи относительно точек А и В соответственно: ХрА =ХА+d1.cos(АР)=12229+3468.cos(164,461о)=8888; УрА =УА+d1.sin(АР)=41182+3468.sin(164,461о)=42111; ХрВ =ХВ+d2.cos(ВР)=16016+7128.cos(179,403о)=8888; УрВ =УА+d2.sin(ВР)=42037+7128.sin(179,403о)=42111. Координаты НП: Хнп=08888, Унп=42111. 48. Обратной засечкой по измеренным расстояниям называется способ определения координат привязываемой точки Р по измеренным на этой точке расстояниям РА, РВ и РС до пунктов А, В и С, координаты которых известны (рис.9). Координаты НП по измеренным расстояниям определяют в следующем порядке: с НП измеряют дальномером или другим способом расстояние до трех исходных точек, положение которых на карте (аэроснимке) и их координаты известны; на карте (планшете, аэроснимке) с контурных точек прочерчивают с помощью измерителя дуги радиусами, соответствующими измеренным расстояниям (в масштабе карты, планшета или аэроснимка); пересечение дуг дает местоположение НП. При получении треугольника погрешностей за положение НП принимают центр треугольника. Если наибольшая сторона треугольника погрешностей превышает 3 мм, то координаты пункта определяют повторно.   В Хв=16016 Ув=42037      (АВ)=2-12 (АР)=27-41     В    АВ  РВ=d2=7128м Р()=2-49  РА=d1= =3468 м  Р (НП) Хр=08888 Ур=42111  А ХА=12229 УА=41182  РС=d3=1835 м  С Хс=82211 Ус=39918 Рис. 9. Засечка по измеренным расстояниям (d1 и d2) и углу (); засечка по измеренным расстояниям (d1, d2, d3) |
