Вопрос 1: Векторный способ задания движения.
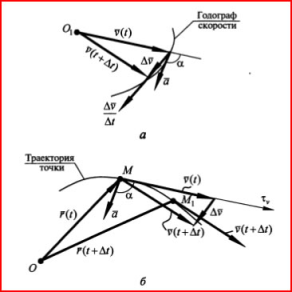
Траектория определяется годографом радиус-вектора точки.
Положение точки М определено, если радиус-вектор rиз центраО выражен функцией времени tr= r(t) задан способ определения модуля вектора и его направления, если имеется система координат. Скорость и ускорение:
tr(t), тогда
(t+Δt)r(t+Δt), получаем
Δr=r(t+Δt)-r(t)
Vср=Δr/Δt. V=lim(Δr/Δt)=dr/dt.
aср=ΔV/Δt. a=lim(Δv/Δt)=dV/dt= d²r(t)/dt².
Переход от векторной формы к координатной:
r(t)=x(t)i+y(t)j+z(t)k.
Обратно:
x=r(t)×i, y=r(t)×j, z=r(t)×k.
|
Вопрос 2:
Движение в декартовой системе координат.
Вектор r можно разложить по базису I, j, k: r=xi+yj+zk.
Движение материальной точки полностью определено, если заданы три непрерывные и однозначные функции от времени t: x=x(t), y=y(t), z=z(t), описывающие изменение координат точки со временем. Эти уравнение называются кинематическими уравнениями движения точки. Радиус-вектор r является функцией переменных x, y, z, которые, в свою очередь, являются функциями времени t. Поэтому производная r׳(t) может быть вычислена по правилу
dr/dt=∂r/∂x∙dx/dt+∂r/∂y∙dy/dt+∂r/∂z∙dz/dt.
Отсюда вытекает, что v=vxi+vyj+vzk.
V=√(vx²+vy²+vz²)
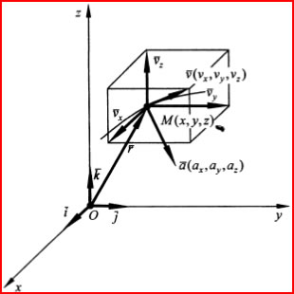
Ускорением точки в данный момент времени назовем вектор а, равный производной от вектора скорости v по времени. А=x׳׳(t)I+y׳׳(t)j+z׳׳(t)k.
А=√((x׳׳(t))²+(y׳׳(t))²+(z׳׳(t))²).
|
Вопрос 3:
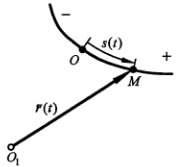
Естественный способ задания движения.
Если задана траектория движения точки, выбрано начало и положительное направление отсчета и известна S=S(t) зависимость пути от времени, то такой способ задания движения точки называется естественным. V=dr/dt∙dS/dS=S׳(t)∙dr/dS=S׳(t)∙τ= =vτ∙τ. Dr/dS=τ. Τ направлена всегда в «+» направлении отсчетаS.
A=dv/dt=S׳׳(t)∙τ+S׳(t)∙dτ/dt=S׳׳∙τ+ (S׳)²n/ρ. Aτ=S׳׳-тангенциальное ускорение, an=(S׳)²/ρ-нормальное (центростремительное) ускорение, ρ-радиус кривизны.
A=√((aτ)²+(an)²).
|
Вопрос 4:
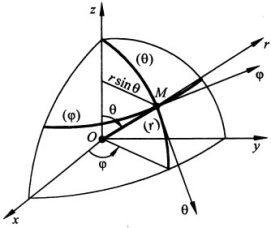
Движение в полярной системе координат.
Ox – полярная ось, φ – полярный угол, r – полярный радиус. Если задан закон r=r(t), φ=φ(t), то задано движение в полярной системе координат. Пусть r=rºr, rº - единичный вектор, pº┴rº - единичный вектор. Тогда v=dr/dt=r׳rº+
rdrº/dt=r׳rº+rφ׳pº=vrrº+vppº. vp и vr – трансверсальная и радиальная составляющая скорости. A=dv/dt=d(r׳rº+rφ׳pº)/ dt=r׳׳rº+r׳drº/dt+r׳φ׳pº+rφ׳׳pº+rφ׳∙
dpº/dt=(r׳׳-(rφ׳)²)rº+(rφ׳׳+2r׳φ׳)pº= ar∙rº+appº.
r²=x²+y², φ=arctg(y/x).
vr=r׳=(xvx+yvy)/r,
vp=rφ׳=(xvy-yvx)/r.
|
Вопрос 5:
Криволинейные координаты. Координатные линии и оси.
Устанавливают закон выбора 3 чисел q1, q2, q3 – криволинейные координаты (обобщенные координаты). Функция координат: r=r(q1,q2,q3) (из точки О).
Возьмем точку М0 с координатами q1,q10,q20.
X=X(q1,q20,q30);
Y=Y(q1,q20,q30);
Z=Z(q1,q20,q30);
r=r(q1, q2, q3)
q=q(t)
Определяют кривую (переменная только q1). Кривая – координатная линия, соответствующая изменению q1 (аналогично q2 и q3). Касательные к координатным линиям, проведенные в точке M0 в сторону возрастания соответствующих координат – координатные оси: [q1], [q2], [q3].
Вдоль каждой из координатных линий изменяется только одна криволинейная координата, а две другие сохраняют постоянные значения, соответствующие рассматриваемой точке.
H1=|∂r/∂q1|=sqrt( (∂x/∂q)^2+(∂y/∂q)^2+(∂z/∂q)^2)- kоэффициент Ламе.
e1=(∂r/∂q1)/H1.
Аналогично Н2, Н3, е2, е3.
|
Вопрос 6:
Скорость точки в криволинейных координатах.
При движении точки ее радиус вектор через обобщенные координаты зависит от времени:
r=r[q1(t),q2(t),q3(t)]
V=dr/dt=(∂r/∂q1)∙dq1/dt+(∂r/∂q2)∙dq2/dt+(∂r/∂q3)∙dq3/dt.
(qi)’=dqi/dt – обобщенная скорость точки.
v=(dq1/dt)H1e1+(dq2/dt)H2e2+(dq3/dt)H3e3.
v=√(dq1/dt)²H1²+(dq2/dt)²H2²+(dq3/dt)²H3². vq1=(dq1/dt)H1, vq2=(dq2/dt)H2, vq3=(dq3/dt)H3.
Пример:
1) скорость в цилиндрической системе.
Т.к. x=ρcosφ, y=ρsinφ, z=z, то
H1=1, H2=ρ, H3=1.
vρ=dρ/dt, vφ=ρdφ/dt, vz=dz/dt.
2) Движение по винтовой.
ρ=R=const, φ=kt, z=ut.
vρ=0, vφ=kR, vz=u.
|
Вопрос 7:
Поступательное движение твердого тела. Траектории, скорости и ускорение точек тела.
Существует 5 видов движения – поступательное, вращательное вокруг неподвижной оси, плоское (плоскопараллельное), сферическое, общий случай. Поступательное движение твердого тела – движение, при котором любая прямая этого тела при движении остается параллельной самой себе.
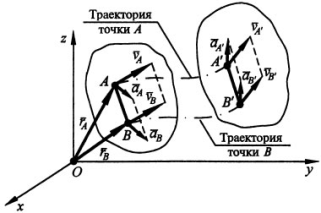
Траектории, скорости и ускорения любой точки тела, совершающего поступательное движение, одинаковы.
Радиус – вектор любой точки движущегося поступательно тела равен rB=rA+AB, AB=const. drB/dt=drA/dt+ dAB/dt=drA/dt =>vB=vA, aB=aA.
Мгновенное поступательное движение – движение твердого тела, для которого векторы скоростей точек равны только в один момент времени.
Поступательное движение полностью характеризуется движением одной точки тела: x=f1(t); y=f2(t);z=f3(t);
|
Вопрос 8:
Вращение твердого тела вокруг неподвижной оси. Скорости и ускорение точек тела.
Вращение твердого тела вокруг неподвижной оси – такое его движение, при котором две точки тела остаются неподвижными в течении всего времени движения.
φ=φ(t) – угол поворота, n=1 степень свободы. Для задания вращения вокруг неподвижной оси необходимо выбрать ось, начало отсчета угла поворота и его положительное направление и задать зависимость угла поворота от времени. ω=dφ/dt – угловая скорость(рад/с). ε=dω/dt= d²φ/dt² - угловое ускорение(рад/с2). Скорость любой точки тела, не лежащей на оси v=ωxr, ускорение a=dv/dt=(dω/dt)xr+ ωxdr/dt=εxr+ωx(ωxr), где aτ=εxr.
Tga=|at|/an=E/ω2 – угол между полным ускорение и радиусом вращения.
Скорость точек тела при вращении вокруг неподвижной оси пропорциональны их кратчайшим расстояниям до этой оси.
U=h*ω – модуль скорости точки.
Частные случаи:
1) ω=const – равномерное вращение (φ=φº+ωt ).
2) ε=const – равноускоренное вращение (ω=ωº+εt, φ=φº+ωt+ εt²/2).
|
Вопрос 9:
Теорема о проекции скоростей двух точек твердого тела на прямую, проходящую через эти точки.
Проекции скоростей двух точек абсолютно твердого тела на прямую, проходящую через эти точки, равны между собой.
Доказательство: Для абсолютно твердого тела имеем:
VB=VA+[Q,AB]
Проектируем это равенство на прямуюLM, проходящую через точки A и B.
ПрLM(VB)= ПрLM(VA)+ ПрLM([Q,AB])
ПрLM([Q,AB])=0 , так как вектор [Q,AB] перпендикулярен прямой LM.
Следовательно, ПрLM(VB)= ПрLM(VA), что и требовалось доказать.
|
Вопрос 10:
Соотношение между скоростями двух точек плоской фигуры при плоском движении твердого тела.
Плоским (плоскопараллельным) назыв. такое движение, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости.
Скорости точек тела при плоском движении: ; , vBA= w×BA, т.е. скорость какой-либо точки В плоской фигуры равна геометрической сумме скорости полюса А и скорости точки В при вращении плоской фигуры вокруг полюса А. Теорема: при плоском движении проекции скоростей двух точек тела на ось, проходящую через эти точки, равны между собой: vAcosa = vBcosb.
|
Вопрос 14:
Соотношение между ускорениями двух точек плоской фигуры при плоском движении.
Ускорение какой-либо точки плоской фигуры при плоском движении равно векторной сумме ускорения полюса и ускорения этой точки от вращательного движения плоской фигуры вокруг полюса.
vB=vA+ωxAB.
aB=dvB/dt=dvA/dt+(dω/dt)xAB+ ωx(dAB/dt)=aA+εxAB+ωx(ωx
AB).
Считая, что εхАВ=(aBA)τ;
(aBA)n=ω²∙AB, окончательно получим:
aB=aA+(aBA)τ+(aBA)n
aA– ускорение полюса;
aBA – ускорение движения вокруг полюса.
|
Вопрос *:
Число степеней свободы твердоготела в общем и частных случаях его движения.
n=3N-k, где n-число степеней свободы, N-число точек, к-число связей. n =6-для свободного тв.тела
Для тела, кот-е совершает сферич.дв-е достаточно 3 коор-ты, поскольку оно имеет 3 степени свободы.
|
Вопрос 11:
Способы определения угловой скорости и ускорения при плоском движении.
Для характеристики вращательной части плоского движения твердого тела вокруг подвижной оси, проходящей через выбранный полюс, аналогично случаю вращения твердого тела вокруг неподвижной оси можно ввести понятие угловой скорости wи углового ускорения E:
w = |dф/dt|; E = |dw/dt| = |d2ф/dt2|.
Угловая скорость и ускорение не зависят от выбора полюса.
Следовательно, для они одинаковы относительно подвижной оси, проходящей через любую точку фигуры.
При плоском движении угловую скорость и ускорение можно считать векторами, направленными по подвижной оси, перпендикулярной плоскости фигуры, и проходящей через выбранный полюс.
wи E– свободные векторы.
|
Вопрос 12:
Мгновенный центр скоростей. Способы нахождения.
При плоском движении твердого тела в каждый момент времени существует точка, скорость которой равна нулю. vP=vO+vPO=0, vO=ω∙OP=>OP= vO/ω.
Если мгновенный центр скоростей известен, то скорости точек плоской фигуры при ее движении в своей плоскости вычисляют так же, как и в случае вращения фигуры в рассматриваемый момент вокруг своего мгновенного центра скоростей с угловой скоростью w.
Если известны скорости двух точек плоской фигуры, мгновенный центр скоростей находится на пересечении перпендикуляров к скоростям этих точек.
Способы нахождения:
на основе физического условия задачи.
На основе предварительного определения скорости двух точек.
|
Вопрос 13:
Определение скоростей точек плоской фигуры с помощью МЦС.
Зная положение МЦС и скорость какой-либо точки фигуры, можно найти скорости всех точек плоской фигуры. Пусть P – МЦС и известна скорость какой-либо точки фигуры vА, тогда ω= vА/AP. vB= vАPB/PA. Соединив конец вектора vB с точкой Р, получим распределение скоростей вдоль отрезка РВ.
Если мгновенный центр скоростей известен, то скорости точек плоской фигуры при ее движении в своей плоскости вычисляют так же, как и в случае вращения фигуры в рассматриваемый момент вокруг своего мгновенного центра скоростей с угловой скоростью w.
|
Вопрос 15:
Способы определения углового ускорения при плоском движении.
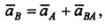 т. е. ускорение какой-либо точки плоской фигуры при плоском движении равно векторной сумме ускорения полюса и ускорения этой точки при вращательном движении плоской фигуры вокруг полюса. т. е. ускорение какой-либо точки плоской фигуры при плоском движении равно векторной сумме ускорения полюса и ускорения этой точки при вращательном движении плоской фигуры вокруг полюса.
Ускорение точки В вокруг А состоит из касательной и нормальной составляющих: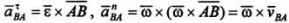
, модули которых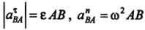
Касательное ускорение направлено перпендикулярно отрезку АВ в сторону, указанную дуговой стрелкой углового ускорения.Нормальное ускорение направлено от точки В к полюсу А. Таким образом,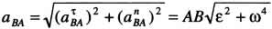
Обозначив угол между ускорением точки В вокруг А и отрезком АВ через "альфа", найдем: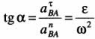
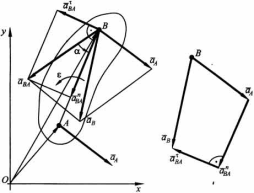
|
Вопрос 16:
Мгновенный центр ускорений. Способы нахождения.
МЦУ – точка плоской фигуры, ускорение которой в данный момент времени равно нулю.
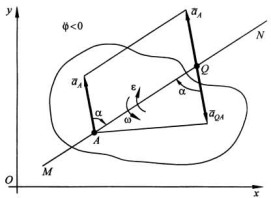
aQ=aA+aAQ=0. Угол между aQA и QAtgα=aBAτ/aBAn=ε/ω², aAQ=√aAQτ+aAQn=AQ√ ε²+ω4
- 1 способ нахождения МЦУ:
Отложить от точки А под углом α=arctg(ε/ω²) к aA отрезок AQ=aA/√(ε²+ω4 в направлении круговой стрелки ε.
- 2 способ нахождении МЦУ основан на условии задачи – если ускорение какой-либо точки по условию задачи равно нулю, то эта точка является МЦУ.
Ускорения точек плоской фигуры при плоском движении можно определить так же, как и при вращательном движении плоской фигуры вокруг мгновенного центра ускорений с угловой скоростью w и угловым ускорение E.
В общем случае мгновенный центры скоростей и ускорений являются различными точками плоской фигуры.
|
Вопрос 17:
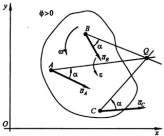
Определение ускорений точек плоской фигуры с помощью МЦУ.
Если МЦУ — точку Q выбрать за полюс, то ускорение любой точки А плоской фигуры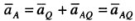 , так как aQ = 0. Тогда , так как aQ = 0. Тогда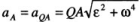 Ускорение аА составляет с отрезком QA, соединяющим эту точку с МЦУ, угол "альфа", откладываемый от QA в сторону, противоположную направлению дуговой стрелки углового ускорения. Ускорения точек фигуры при плоском движении пропорциональны расстояниям от МЦУ до этих точек. Ускорение аА составляет с отрезком QA, соединяющим эту точку с МЦУ, угол "альфа", откладываемый от QA в сторону, противоположную направлению дуговой стрелки углового ускорения. Ускорения точек фигуры при плоском движении пропорциональны расстояниям от МЦУ до этих точек.
Таким образом, ускорение всякой точки фигуры при ее плоском движении определяется в данный момент времени так же, как и при вращательном движении фигуры вокруг МЦУ.
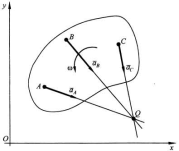
1) Пусть известны направления ускорений двух точек плоской фигуры, ее угловые скорость и ускорение. Тогда МЦУ лежит на пересечении прямых линий, проведенных к векторам ускорений точек фигуры под одним и тем же острым углом:,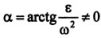 отложенным от векторов ускорений точек в направлении дуговой стрелки углового ускорения. отложенным от векторов ускорений точек в направлении дуговой стрелки углового ускорения.
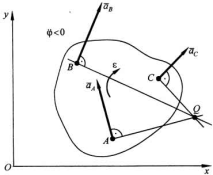
2) Пусть известны направления ускорений хотя бы двух точек плоской фигуры, ее угловое ускорение = 0, а угловая скорость не равна 0.
3) Угловая скорость = 0, угловое ускорение не равно 0. Угол прямой.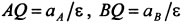
|
Вопрос 18:
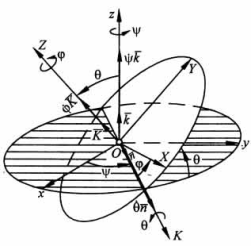
Вращение твердого тела вокруг неподвижной точки. Углы Эйлера.
Движение твердого тела, у которого одна точка неподвижна, называется сферическим. Количество степеней свободы n=3. (XA, YA, ZA).
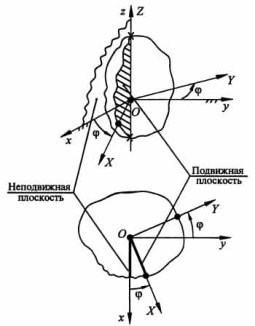
Положение тела определяется с помощью углов Эйлера. Определение: свяжем с телом подвижную систему координат Oxyz. Плоскость xOy пересекает неподвижную плоскость x1Oy1 по прямой ОК – линии узлов.
Ψ – угол прецессии;
φ – угол собственного вращения
θ – угол нутации.
Все углы против часовой стрелке.
Если заданы функции Ψ=f1(t); φ=f2(t); θ=f3(t) то движение полностью определено.
|
Вопрос 19:
Скорости и ускорения точек тела при его вращении вокруг неподвижной точки.
VA=ω×rA. Пусть точка М лежит на мгновенной оси вращения.
i j k
VM=ω×rM= ωxωyωz
XMYMZM
X/ωx=Y/ωy=Z/ωz – мгновенная ось вращения.
aA=dv/dt=dω/dt×rA+ω×drA/dt=ε×rA+ω×vA=aAвр+aAос.
aAвр=ε×rA – вращательное ускорение точки.
aAос=ω×vA – осестремительное ускорение точки.
Формула Ривальса: aAoc=ωvAsin(ω, vA). aвр направлен перпендикулярно плоскости (ε,r) в сторону, откуда переход от ε к r виден против часовой стрелки.
aвр направлен по перпендикуляру к плоскости (ω,v).
Скоросте точек тела пропорциональны рассточниям от этих точек до мгновенной оси.
| |
 Скачать 1.21 Mb.
Скачать 1.21 Mb.