теормех шпоры. Вопрос 1 Векторный способ задания движения

• Название: Вопрос 1 Векторный способ задания движения
• Анкор: теормех шпоры
• Дата: 08.12.2022
• Размер: 1.21 Mb.
• Имя файла: Termekh_shpory_1.doc
• Тип: Документы; #835510
• страница: 2 из 3

Вопрос 20:

Скорости и ускорения точек твердого тела при его свободном движении.

Разложение общего вида движения на поступательное, связанное с точкой О и вращательное относительно О.

Переносное движение - поступательное движение вместе с полюсом. (Ve)

Относительное движение - вращательное движение относительно полюса. (Vr)
Поступательное:

X_1o=f₁(t); Y_1o=f₂(t); Z_1o=f₃(t).

Вращательное:

Ψ=f₄(t); φ=f₅(t); θ=f₆(t).

Таким образом, число степеней свободы при свободном движении твердого тела равно 6.

ρ_A=ρ_о+rv_A=dρ/dt+dr/dt=v_o+ω×r.

a_A=dv_A/dt=dv_o/dt+dω/dt×r+ω×dr/dt=a_o+ε×r+ω²r=a_o+a_A^вр+a_A^ос.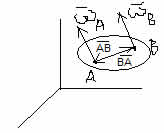



1) Полюс - т. А: vB = vA + ωS*AB

2) Полюс - т. В: vA = vB + ωB*BA = vB - ωB*AB

1) + 2) : (vB + vA) = (vA + vB) + ω*AB- ωB*AB

(ωA - ωB)*AB = 0

Вопрос 21:

Сложное движение точки. Основные понятия.

Сложное движение – движение по отношению к системе координат, выбранной за основную (абсолютную).

Относительное движение – движение точки по отношению к подвижной системе координат.

Переносное движение – движение подвижной системы координат относительно неподвижной. Установление связи между этимидвижениями позволяет решать различные задачи.

Положение точки М в подвижной системе координат O'XYZ характеризует радиус-вектор с началом в точке О'. Траектория точки М в подвижной системе отсчета называется относительной траекторией и представляет собой годограф радиус-вектора Скорость движения точки М по отношению к осям подвижной системы координат называется относительной скоростью и обозначается Vr. Вектор Vr определяет скорость изменения с течением времени радиус-вектора в подвижной системе O'XYZ и поэтому выражается его относительной, или локальной, производной по времени,

Ускорение точки М в этом движении называется относительным ускорением и обозначается аr. Вектор аr характеризует скорость изменения вектора относительной скорости Vr в подвижной системе O'XYZ и поэтому выражается относительной, или локальной, производной по времени от Vr:

Движение подвижной системы O'XYZ по отношению к неподвижной Oxyz является для точки М переносным движением, а скорость и ускорение той неизменно связанной с подвижной

системой отсчета точки А, с которой в данный момент времени совпадает точка М, называют переносными скоростью и ускорением точки М и обозначают Ve и ае.

Переносные скорость и ускорение точки М определяются по формулам: , где вектора Vo' и ao' - скорость и ускорение точки О' подвижной системы координат.

Вопрос 22:

Полная и локальная производные вектора. Формула Бура.

Рассмотрим изменение вектора b(t) по отношению к двум системам координат — подвижной O'XYZ и неподвижной Oxyz.

Абсолютной, или полной, производной вектора b по аргументу t назьшается вектор определяющий изменение вектоpa b(t) в неподвижной системе Oxyz.

Относительная, или локальная, производная определяет измененине вектора b(t) в подвижной системе O'XYZ.

Формула Бура (получается из зависимости между полной и локальной производными):

Рассомтрим частные случаи.

1) угловая скорость = 0, то

2) вектор b не меняется в подвижной системе отсчета =0), то

3) , т.е. вектор b все время параллелен вектору угловой скорости ( ), то = . В частности, если , то , т.е. вектор угловой скорости изменяется одинаково для подвижной и неподвижной систем координат.

Выведение формулы Бура:

Найдем зависимость между полной и локальными производными. Если воспользоваться проекциями вектора b(t) на оси подвижной системы O'XYZ, то можно записать: , где I, J, К — орты, не изменяемые в этой системе отсчета. Поэтому локальная производная , а полная производная с учетом изменения также ортов I, J , К имеет вид: . В правой части уравнения первые три слагаемых выражают локальную производную, а производные от ортов I, J, K определяются формулами Пуассона ( ), т.е. . С учетом получаем: .

Вопрос 23:

Скорости и ускорения точки при сложном движении.

ρ = r0 + r

dp/dt = d(r0+r)/dt = dr0/dt + dr/dt

dp/dt = v0 + dr/dt + ω*r = v0 + vr + ω*r

v = v0 + ω*r + vr = ve + vr

a = dv/dt = d(v0 + ω*r +vr)/dt = a0 + (dω/dt)*r + ω*(dr/dt) + dvr/dt

dr/dt = d()r/dt + ω*r = vr + ω*r

dvr/dt = d()vr/dt + ω*vr = ar + ω*vr

a = a0 + ε*r + ω*vr + ω*vr + ω*(r*ω) + ar + ω*vr = a0 + a(вр) + ω*vr + ω*vr + а(ос) + ar + ω*vr

a = a0 + ε*r + ω*(r*ω) + ar + + 2*ω*vr, где 2*ω*vr - добавочное (поворотное) ускорение, a0 + ε*r + ω*(r*ω) - (ае) переносное ускорение.

Опр-е ускорения точки в сложном движении

V_M=V_O+[ ωr]+ V_r

W_M=dV_M/dt=(dV_O/dt)+[ εr]+[ ω(dr/dt)]+dV_r/dt

dr/dt=[ ωr]+ V_r

W_M=W_o+[ εr]+ [ω[ωr]]+[ ωV_r]+ [ ωV_r]+W_r

dV_r/dt=[ ωV_r]+ W_r

W_k=2[ωV_r]

W_M=W_L+W_r+W_K – кинематическая теорема Кариолиса

Абсолютное ускорение точки –это есть сумма переносного ускорения, относительного ускорения и ускорения Кариолиса

Переносное ускорение хар-етизмен-е переносной скорости в переносном движении.

Относительное ускорение хар-етизм-е относительнойскоростив в относительном движении. Ускорение Кариолисахар-етизм-е относительной скорости в переносном движении

Ускорение Кариолиса.

Согласно правилу векторного произведения, вектор ускорения Кариолиса┴пл-ти, в кот-й лежат вектора ω и V_r и направлена в ту сторону,что с конца этого вектора кратчайшее совмещение первого вектора ко второму ω к V_r кажется видным против хода часовой стрелки.

Вопрос 24:

Ускорение Кориолиса. Правило Жуковского.

Кинематическая теорема Кориолиса: абсолютное ускорение точки является векторной суммой трех ускорений - относительного, переносного и ускорения Кориолиса.

Ускорение Кориолиса равно удвоенному векторному произведению угловой скорости переносного движения на относительную скорость точки: , следовательно по модулю ускорение Кориолиса: (sin90=1).

Кориолисово ускорение обращаетсяв нуль, когда:

1) переносное движение - поступательное, т.е. омега переносное равно нулю;

2) в те моменты времени, когда в относительном движении точка останавливается, например.при изменении направления относительного движения.

Частные случаи:

А) ω0 – смена знака

Б) v_r0 – относительный покой (смена знака движения).

В) sin(ω,v_r)0, ω||v_r.

Правило Жуковского: Кориолисово ускорение можно получить, спроецировав вектор радиальной скорости на плоскость, перпендикулярную вектору омега переносное, увеличив полученную проекцию радиальной скорости в 2*(омега переносное) раз и повернув ее на 90 градусов в направлении переносного вращения.

Вопрос 25:

Сложное вращение твердого тела вокруг пресекающихся осей.

В случае вращательных относительного и переносного движений твердого тела, когда оси их вращений пересекаются в точке О (рис. 7.2), абсолютное движение будет движением твердого тела вокруг неподвижной точки О (сферическим движением) с угловой скоростью, определяемой согласно



Нетрудно убедиться, что скорости всех точек, лежащих на линии, по которой направлен вектор угловой скорости, равны нулю. В самом деле, например, скорость находящейся на этой линии точки А тела (по свойству произведения коллинеарных векторов "омега" и r). Таким образом, прямая, на которой расположен вектор угловой скорости, является мгновенной осью вращения тела.

Скорость любой точки М тела в данном случае можно определить так: или , где

Модули составляющих, а также абсолютной скорости точки М равны модулям соответствующих векторных произведений и могут быть вычислены по формулам: , где - кратчайшие расстояния от точки М до соответствующих осей вращения.

Вопрос 26:

Сложное вращение твердого тела вокруг параллельных осей.

Если оси вращательных движений тела параллельны, то вектор результирующей угловой скорости ω тела в неподвижной системе координат будет коллинеаренω_е и ω_r. Положение мгновенной оси вращения тела как оси, проходящей в данный момент времени через точку Р – МЦС в плоскости П, перпендикулярной осям вращений, можно определить из анализа: v_rP=ω_r×O_rP, v_eP=ω_e×O_eP, O_r, O_e – точки пересечений П с соответствующими осями вращения. v_P=v_eP+v_rP=0v_eP= -v_rPv_eP= v_rPω_rO_rP=ω_eO_eP.

В зависимости от взаимного расположения и численного значения векторов ω_r и ω_e можно выделить 3 случая сложения вращательных движений:

А) При совпадении направлений векторов ω_e и ω_r абсолютное движение будет плоским. Абсолютная угловая скорость в этом случае будет иметь направление, совпадающее с направлениями её составляющих, а её модуль ω=ω_r+ω_e. Положение точки Р можно найти из пропорции ω_e/O_rP=ω_rO_eP=ω/O_eO_r. Скорость любой точки тела может быть найдена по формуле v=ω×PM.

Б) При противоположных направлениях векторов ω_e и ω_r, когда ω_r≠ω_e, абсолютное движение будет плоским. Абсолютная угловая скорость имеет направление, совпадающее с направлением большей по модулю составляющей угловой скорости, а её модуль ω=|ω_r-ω_e|. Пропорции для нахождения точки Р имеют тот же вид, что и в пункте А.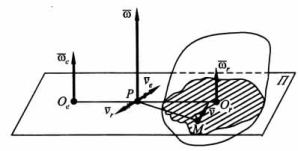

Вопрос 27:

Пара вращений.

При противоположных направлениях векторов ω_e и ω_rи равенстве их модулей (ω_e = ω_r), если условие ω_e=-ω_r выполняется на отрезке времени t₂-t₁, абсолютное движение будет поступательным. Такой случай сложения вращательных движений называется парой вращений.

Действительно, ω=ω_e+ω_r=

-ω_r+ω_r=0, и для любой точки тела справедливы соотношения: v=ω_e×r₁+ω_r×r₂=ω_e×(r₁-r₂)=ω_e×O_eO_r=ω_r×O_rO_e;

Следовательно, скорости всех точек тела в данном случае одинаковы и равны скорости поступательного движения.

Вопрос 28:

Аксиомы статики.

1. 
   2 силы, приложенные к абс. твердому телу будут эквивалентны 0 тогда и только тогда, когда они равны по модулю, действуют на одной прямой и направлены в противоположные стороны.
   

Следствие. Сумма всех внутренних сил всегда равна нулю.

2. 
   Действие данной системы сил на абсолютно твердое тело не изменится, если к ней добавить или отнять систему сил, эквивалентную 0 => точку приложения силы можно переносить вдоль линии её действия.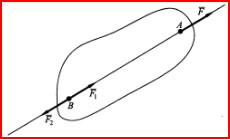
   

3. 
   Если к телу приложены 2 силы, исходящие из одной точки, то их можно заменить равнодействующей (любую силу можно разложить на составляющие бесконечное число раз).
   
4. 
   Силы взаимодействия двух тел равны по модулю и противоположны по направлению.
   
5. 
   Механическое состояние системы не изменится, если освободить ее от связей, приложив к точкам системы силы, равные реакциям связей.
   

Действие связей можно заменить действием сил – реакций связи.

Вопрос 29:

Основные виды связей и их реакции.

Связи – ограничения, накладываемые на свободное твердое тело (занимает произвольное положение в пространстве). Реакция связи направлена в сторону, противоположную той, куда связь не дает перемещаться телу.

1. 
   Гладкая поверхность – по общей нормали.
   

2. 
   Нить – вдоль к точке закрепления.
   

3. 
   Цилиндрический шарнир (подшипник)
   

4. 
   Сферический шарнир – по любому радиусу.
   

5. 
   Подпятник, подшипник – любое направление.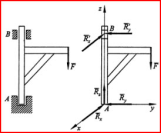
   

6. 
   Невесомый стержень с шарнирами на концах. Реакция прямолинейного невесомого стержня с шарнирами на концах направлена вдоль оси стержня. В отличае от нити такой стержень может передавать как силы растяжения, так и силы сжатия.
   

Дополнительно:

А) Скользящий;

Б) Внутренний.

Вопрос 30:

Система сходящихся сил. Условия равновесия.

Система сил называется сходящейся, если линии всех сил пересекаются в одной точке. Попарно поочередно сложим эти силы, перенесенные к точке пересечения. Тогда R=∑F_k – главный вектор, так как R₁₂=F₁+F₂, R₁₃=R₁₂+F₃ и т. д.

R_x=∑F_ixR=√(R_x²+R_y²+R_z²), cos(x,R)=R_x/R – аналитический способ задания.

Условия равновесия.

Система находится в равновесии когда главный вектор R=0.

А) Векторная форма: R=∑F_k=0;

Б) Аналитическая форма: R_x=F_kx=0, R_y=F_ky=0, R_z=F_kz=0;

В) Графическая форма: замкнут многоугольник сил.

Система сходящихся сил эквивалентна одной равнодействующей силе, которую можно определить замыкающим вектором R* силового многоугольника, построенного на векторах-сипах системы сходящихся сил. Другими словами, равнодействующая системы сходящихся сил равна их геометрической сумме.



Многоугольник OABCD называется силовым многоугольником

Вопрос 31:

Алгебраический и векторный моменты силы относительно точки.

Алгебраическим моментом М=+-F*d( пара ). Он не меняется при перемещении сил вдоль линии их действия ( ни плечо, ни направления вращения не меняются).

Векторный момент – вектор М=М(F,F*), направлен перпендикулярно плоскости пары в ту сторону, откуда видно стремление пары повернуть тело против часовой стрелки, его модуль равен алгебраическому моменту пары.
Момент относительно точки.

Алгебраическим моментом силы Fотносительно точки О называется взятое со знаком «+» или «-» произведение |F| на ее плечо: M₀(F)=+-Fh. «+» - против часовой стрелки. Характеризует вращательный эффект F.

Свойства:

А) Не меняется при переносе точки приложения вдоль линии действия силы ( т.к. |F|sinA=const).

Б) М=0 если т.О лежит на линии действия силы. Плоскость действия М -через F и О.

Векторный момент силы Fотносительно точки О – вектор M₀(F)=r*F (r–радиус вектор из А в О). |M₀(F)=|F|*|r|*sinA=Fh.|

ijk

M_O(F)= x_Ay_Az_A=>

F_xF_yF_z

• 
  M_Ox(F)=yF_z-zF_y
  
• 
  M_Oy(F)=zF_x-xF_z
  

M_Oz(F)=xF_y-yF_x

Теорема Вариньона - момент равнодействующий относительно какой-либо точки равен сумме моментов сил ее составляющих.

Вопрос 32:

Момент силы относительно оси.

Момент силы относительно оси – алгебраический момент проекции этой силы на ось, перпендикулярную оси z, взятого относительно точки A пересечения оси с этой плоскостью. Характеризует вращательный эффект относительно оси.

M_z(F)=2S_ΔABC=F_┴∙h.

Если M_z(F)=0, то сила F либо параллельна оси z, либо линия её действия пересекает ось z.

Второе правило определения момента силы относительно оси: Момент силы относительно оси называется произведение проекции силы на плоскость перпендикулярную оси на плечо этой проекции относительно точки пересечения плоскости с осью.

Момент силы относительно оси Z: M0z(F) = ±hп * Fп
Частные случаи: момент силы относительно оси = 0.

а) Fп = 0



б) hп = 0 (сила пересекает ось)

Момент силы относительно оси = 0, если сила и ось находятся в одной плоскости.

Момент сил относительно декартовых осей координат (проекции момента силы на эти оси).
| i j k |

M0(F) = r * F = | x y z | = (y*Fz - z*Fy)*i + (z*Fx - x*Fz)*j + (x*Fy -

| FxFyFz |

y*Fx)*k = Mox(F)*i + Moy(F)*j + Moz(F)*k
Mox(F)=y*Fz - z*Fy

Moy(F)=z*Fx - x*Fz

Moz(F)=x*Fy - y*Fx

Вопрос 33:

Связь векторного момента силы относительно точки с моментом силы относительно оси, проходящей через эту точку.

Момент силы F относительно оси z равен проекции на эту ось вектора момента силы Fотносительно произвольной точки О на этой оси.

Доказательство:

Пусть О – произвольная точка на оси z. Момент силы F относительно точки О перпендикулярен плоскости ОАВ

M_O(F)┴(OAB). Пусть угол междуM_O(F) и осью z равен α. Тогда Пр_zM_O(F)=2S_{ΔO’A’B’}= 2S_ΔOAB∙cosα =>M_z(F) = |M_O(F)|cosα.

Ч.т.д.
2*S(OA'B') = 2*S(OAB)*cosα

| Moz(F) | = | Mo(F) |*cosα

MCOO = проекции на эту ось векторному МСОТ

Вопрос 34:

Аналитические выражения для моментов силы относительно осей координат.

Используя связь момента силы относительно оси с векторным моментом силы относительно точки на оси, можно получить формулы для вычисления моментов относительно осей координат, если даны проекции силы на оси координат и координаты точки приложения силы.

i j k

M_O(F)= x_Ay_Az_A=>

F_xF_yF_z

• 
  M_Ox(F)=yF_z-zF_y
  
• 
  M_Oy(F)=zF_x-xF_z
  

M_Oz(F)=xF_y-yF_x

По этим формулам получают необходимые знаки для M_Ox(F), M_Oy(F), M_Oz(F) если проекция силы Fна оси координат и координаты x,y,zточки приложения силы подставлять в них со знаками этих величин.

При решении задач момент силы относительно какой-либо оси часто получают, используя его определение, т.е. проецируя силу на плоскость, перпендикулярную оси, и вычисляя затем алгебраический момент этой проекции относительно точки пересечения оси с этой плосколстью.

Вопрос 35:

Пара сил. Теорема о сумме моментов сил, составляющих пару, относительно произвольной точки.

Пара сил - система двух сил равных по модулю и противоположных по направлению.



F1 = -F2

R* = F1 - F2 = 0

AC/F2 = BC/(R*) (стремится к бесконечности)

(F1,F2) не эквивалентны 0

Момент пары сил - произведение одной из сил на ее плечо.

M(F1,F2) = M12 = ±F1*d = ±F2*d

Векторный момент пары сил.



MA = AB * F2

MA = F2 * AB * sinα = F2d

MB = BA * F1 = F1 * d

M = MA = MB = S(ACBD)
Теорема о сумме моментов сил, составляющих пару, относительно произвольной точки: Сумма моментов сил, входящих в состав пары сил относительно любой точки не зависит от ее выбора и равна моменту этой пары сил.



F1 = -F2

Mo(F2) + Mo(F1) = r2*F2 + r1*F1 = r2*F2 - r1*F2 = (r2 - r1)*F2 = AB * F2 = M(F1,F2)

Теорема Пуассо: Произвольная система сил, действующих на твердое тело, можно привести к какому-либо центру О, заменив все действующие силы главным вектором системы сил R, приложенным к точке О, и главным моментом M_O системы сил относительно точки О.

Доказательство:

Пусть О – центр приведения. Переносим силы F₁, F₂,…,F_n в точку О: FO=F₁ +F₂+…+F_n= ∑F_k. При этом получаем каждый раз соответствующую пару сил (F₁,F₁”)…(F_n,F_n”), Моменты этих пар равны моментам этих сил относительно точки О. M₁=M(F₁,F₁”)=r₁xF₁=M_O(F₁). На основании правила приведения систем пар к простейшему виду M_O=M₁+…+M₂=∑M_O(F_k)= ∑r_kxF_k => (F₁, F₂,…,F_n) (R,M_O) (не зависит от выбора точки О).

Вопрос 36:

Векторный и алгебраический моменты пары сил.

Алгебраический момент M=F∙d (пара). M=dF₁=dF₂=2S_ΔABC= S_ٱ. Он не меняется при перемещении сил вдоль линии их действия (ни плечо, ни направление вращения не меняются).

Векторный момент – вектор M=M(F,F’), направлен перпендикулярно плоскости пары в ту сторону, откуда видно стремление пары повернуть тело против часовой хода стрелки, его модуль равен алгебраическому моменту пары.

M(F₁,F₂)=BAxF₁=ABxF₂.

Моменты относительно точки.

Алгебраическим моментом силы F относительно точки О называется взятое со знаком «+» или «-» произведение |F| на её плечо: M_O(F)=Fh=2S_ΔOAB∙ M_O(F). «+» - против часовой стрелки. Характеризует вращательный эффект F.

Свойства:

А) Не меняется при переносе точки приложения вдоль линии действия силы. (т.к. |F|sinα= const).

Б) Ь=0 если т. О лежит на линии действия силы.

Плоскость действия M – через F и O.

Векторный момент силы F относительно точки О – вектор M_O(F)=rxF (r – радиус- вектор из А в О). |M_O(F)|=|F|∙|r|∙sinα=Fh.

ijk

M_O(F)= x_Ay_Az_A=>

F_xF_yF_z

• 
  M_Ox(F)=yF_z-zF_y
  
• 
  M_Oy(F)=zF_x-xF_z
  

M_Oz(F)=xF_y-yF_x

Вопрос 37:

Эквивалентность пар. Сложение пар. Условия равновесия пар сил.

Эквивалентность: А) 2 пары, имеющие равные моменты, эквивалентны. Пару сил можно перемещать, поворачивать в плоскости действия, перемещать в параллельную плоскость, менять одновременно силу и плечо.

Б) 2 пары, лежащие в одной плоскости, можно заменить на одну пару, лежащую в той же плоскости с моментом, равным сумме моментов этих пар.

M=M(R,R’)=BA×R=BA×(F₁+F₂)=BA×F₁+BA×F₂. При переносе сил вдоль линии действия момент пары не меняется BA×F₁=M₁, BA×F₂=M₂, M=M₁+M₂.

СЛОЖЕНИЕ. 2 пары, лежащие в пересекающихся плоскостях, эквивалентны 1 паре, момент которой равен сумме моментов двух данных пар.

Дано: (F₁, F₁’), (F₂, F₂’)

Доказательство:

Приведем данные силы к плечу АВ – оси пересечения плоскостей. Получим пары:

(Q₁,Q₁’) и (Q₂,Q₂’). При этом M₁=M(Q₁,Q₁’)=M(F₁, F₁’),

M₂=M(Q₂,Q₂’)=M(F₂, F₂’).

Сложим силы R=Q₁+Q₂, R’=Q₁’+Q₂’. Т. к. Q₁’= - Q₁, Q₂’= - Q₂R= -R’. Доказано, чтосистемадвухпарэквивалентнасистеме (R,R’). M(R,R’)=BA×R=BA×(Q₁+Q₂)= BA×Q₁+BA×Q₂=M(Q₁,Q₁’)+ M(Q₂,Q₂’)=M(F₁,F₁’)+ M(F₂,F₂’) M=M₁+M₂.

УСЛОВИЯ РАВНОВЕСИЯ:

Система находится в равновесии, если суммарный момент всех пар сил, действующих на тело, равен нулю.

M₁+ M₂+…+M_n=0.

Вопрос 38:

Лемма о параллельном переносе силы.

Сила, приложенная к какой-либо точке твердого тела, эквивалентна такой же силе, приложенной к любой другой точке тела, и паре сил, момент которой равен моменту данной силы относительно новой точки приложения.



Доказательство: пусть дана сила F. Приложим к какой-либо точке В систему F’ и F”.

|F|=|F’|=|F”|. F(F,F’,F”), т.к. (F’,F”) 0, то

F (F,F’,F”) (F,F’,F”) (F’,M(F,F”)).

НоM(F,F”)=BAxF=M_B(F).

Получаем:

F (F’,M(F,F”))

Ч. т. д.

Вопрос 39:

Теорема о приведении произвольной системы сил к силе и паре сил - основная теорема статики.

Теорема Пуассо: Произвольная система сил, действующих на твердое тело, можно привести к какому-либо центру О, заменив все действующие силы главным вектором системы сил R, приложенным к точке О, и главным моментом M_O системы сил относительно точки О.



Доказательство:

Пусть О – центр приведения. Переносим силы F₁, F₂,…,F_n в точку О: FO=F₁ +F₂+…+F_n= ∑F_k. При этом получаем каждый раз соответствующую пару сил (F₁,F₁”)…(F_n,F_n”), Моменты этих пар равны моментам этих сил относительно точки О. M₁=M(F₁,F₁”)=r₁xF₁=M_O(F₁). На основании правила приведения систем пар к простейшему виду M_O=M₁+…+M₂=∑M_O(F_k)= ∑r_kxF_k => (F₁, F₂,…,F_n) (R,M_O) (не зависит от выбора точки О).
При приведении системы сил к заданому центру возникает главный вектор R равный сумме всех сил и главный момент Мо, равный сумме моментов всех сил относительно центра приведения.

Вопрос 41:

Главный вектор и главный момент системы сил.

Пусть дана система сил (F₁, F₂,…,F_n).

Главным вектором системы сил называется вектор, равный векторной сумме этих сил.

R=∑F_k.

R_x=∑F_kx; cos(x,R)=R_x/R;

R_y=∑F_ky; cos(y,R)=R_y/R;

R_z=∑F_kz; cos(z,R)=R_z/R;



Главный момент системы сил – сумма моментов сил относительно какого-либо полюса (центра приведения).

L_x=∑M_x(F_k)
R0 - главный вектор

L0 - главный пучок моментов сил

Главный вектор не зависит от точки приведения, а главный момент зависит.

Главный момент системы сил относительно точки О называют сумму векторных моментов всех сил системы относительно этой точки.

Вопрос 42:

Условия равновесия произвольной системы сил. Частные случаи.

R=0 и L_o=0 –ур-я равновесия. Им соотв-ют 6 скалярных алгебраических ур-1 равновесия для простр.системы сил:

F_kх=0 F_kу=0 F_kz=0 М_х(Fk)=0 Му(Fk)=0 Мz(F_k)=0 – аналитическое условие равновесия для произвольной системы сил.

Пусть все силы пл-тихоу, тогда: F_kх=0 F_kу=0 Мо(Fk)=0 условие равновесия для произвольной плоской системы сил.

Условие равновесия для плоской системы параллельных сил.

Пустьсилы оси оу, тогда F_kх=0 Мо(Fk)=0

Условие равновесия для пространственной системы параллельных сил.

F₁, F₂, F₃,…,F_n оси оz, тогда: F_kz=0 М_х(Fk)=0 Му(Fk)=0