Вторая форма условия равновесия для пороизвольной плоской системы сил:
МА(Fk)=0 МВ(Fk)=0 МС(Fk)=0 – причемт.А, т,В, т.С одной прямой.
- Докажем необходимость этих условий:
Допустим, система сил нах-ся в равновесии. Тогда очевидно, что моментов всех сил относительно любой точки пл-ти=0, т.е. выполняются эти 3 условия.
- Докажем достаточность этих условий:
Доказать достоточность – это значит доказать, что при выполнении этих усл-й система нах-ся в равновесии. Доказывать будем методом от противного, поэтому предположим, что эти усл-я выполняются, но система не нах-ся в равновесии, т.е. существует R*0 эквив.даннойсист.сил.
Рассмотрим усл-е первое и 2-е: для того, чтобы они выполнялись необходимо, чтобы R* проходил через т.А и т.В. Согласно третьему условию hR=0. Поскольку т.С прямой АВ это может выполняться только в случае R*=0, т.е. наше предположение не верно и система действительно нах-ся в равновесии.
Третья форма усл-я равновесия для произвольной плоской системы сил.
Fkz=0 МА(Fk)=0 МВ(Fk)=0 – причем ось ох не перпендикулярна АВ.
- Необходимость этого усл-я очевидна, т.к.если система нах-ся в равновесии, то главный вектор и главный момент =0 относительно любой точки.
- Докажем достаточность этих условий:
Предположим, что система не нах-ся в равновесии и сущ-ет, т.е. сущ-етR* и R* 0 является равнодействующей данной системы сил. Для того, чтобы выполнялось усл-е 2 и 3 необходимо, чтобы R* проходил через АВ.
Потребуем выполнения усл-я R*cos=0, поскольку х не перпендикулярна АВ , то R* должно быть равно 0, т.о. мы доказали, что эти усл-я достаточны для того чтобы система находилась в равновесии.
На основании двух изложенных форм ур-й равновесия для плоской системы параллельных сил можно записать еще один вид ур-я равновесия для плоской системы параллельных сил:
МА(Fk)=0 МВ(Fk)=0, АВ не параллельнаF1, F2, F3,…,Fn
Вопрос 43:
Теорема Вариньона о моменте равнодействующей силы.
Если данная система сил имеет равнодействующую, то момент равнодействующей относительно произвольной точки О равен сумме моментов относительно той же точки.
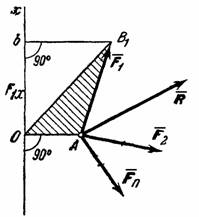
Пусть система сил (F1, F2,…,Fn) приводит к равнодействующей R, проходящей через точку С пересечения линий действия сил. Возьмем произвольную точку О, тогда:
MO(R)=rxR=rx∑Fi=∑(rxFi)= ∑MOi(Fi).
Ч. т. д..
|
Вопрос 44:
Зависимость между главными моментами системы сил относительно двух центров приведения.
Главный момент системы сил относительно второго центра приведения О1 равен вектору главного момента системы сил относительно первого центра приведения О, плюс векторный момент главного вектора, приложенного в первом центре приведения относительно второго центра.
Доказательство:
Момент относительно любой точки O1 MO1=∑(rO1ixFi). Момент относительно первого центра приведения ОMO=∑(rOixFi). ПричемrO1i=O1O+rOi.
MO1=∑(O1O+rO1)xFi=O1O∑Fi+ ∑(rOixFi)=MO+O1OxR= MO+MO1(R).
MO1= MO+MO1(R) (1)
|
Вопрос 45 (1):
Инварианты системы сил. Частные случаи приведения.
Инвариант системы сил – векторные и скалярные величины, не зависящие от точки приведения системы сил.
Главный вектор R=∑Fi=const.
Скалярное произведение главного вектора и главного момента LOR=const=FxMx+ FyMy+FzMz.
Доказательство: Умножим обе части выражения (1) на R:
MO1R= MOR+(O1OxR)RПрR(LO1)= ПрR(LO)=LO1R∙ ∙cos(LO1^R)= LO2Rcos(LO2^R).
LO1xRx+ LO1yRy +LO1zRz =LO2xRx +LO2yRy +LO2zRz
Приведение к простейшему виду:
MO=0, R0 к равнодействующей, равной R, проходящей через О.
R=0, MO0 к паре с моментом MO(независимо от О).
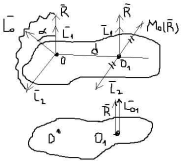
R0, MO0, MO┴Rк равнодействующей, равной R, проходящей через О1: ОО1=d= |MO| / |R|. Доказательство: R и пара сил с моментом MO лежат в одной плоскости
силы R и R” уравновешиваются, систему можно заменить равнодействующей R’.
MOR0, R0, MO0, R не перпендикулярна MO – приводится к динаме.
Доказательство: Разложим MO на 2 составляющих: M1 иM2. M2 представим в виде пары сил R’ и R”. Силы Rи R” уравновешиваются, а M1перенесем в точку O1 (свободы).
В результате получили винт R’,M1, проходящий через точку О1.
Прямая, проходящая через точку О1 – ось динамы.
|
Вопрос 45 (2):
Инварианты системы сил. Частные случаи приведения.
Инварианты в статике, такие величины, для рассматриваемой системы сил, которые не изменяются при изменении центра приведения.
Виды инвариантов:
1) Векторный инвариант - главный вектор системы сил (R);
2) Скалярный инвариант.
L0 * R = L01 * R
L01 = L0 + O1O * R
L01 * R = L0 * R + (O1O * R) * R = L0*R + (R * R) * O1O
L01 * R = L0 * R
Скалярное произведение главного вектора на главный момент не зависит от центра приведения.
L01 * R * cosα = L0 * R * cosα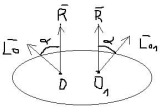
L01 * cosα = L0 * cosα
Проекция главного момента на шлавный вектор не зависит от центра приведения.
Частные случаи приведения системы сил:
1) Приведение к паре сил.
В этом случае система сил приводится к одной паре.
R0 = R = 0
L01 = L0 + O1O * R
2) Приведение к равнодействующей.
а) Если L0 = 0, то R = R*.

Линия действия проходит через центр приведения.
б) Если R≠0 , L0≠0, но R перпендикулярен L0.
OY перпендикулярен (L0,R)
d= L0 / R = OO1
| M01(R) | = d * R = L0
Отбросим (L,M0(R)), т.к. 0 и останется R*.
Плоская система сил всегда может быть приведена к равнодействующей.
Приведение к динамическому винту (к динаме).

Динамический винт - такая совокупность главного момента и главного вектора, когда векторы параллельны.
L0 = L1 + L2
|L1| = L0 * cosα
L2 = L0 * sinα
d = L2 / R
M01(R) = O1O * R
L0 * R = L0 * R * cosα = LxRx + LyRy + LzRz
L0 = Lxi + Lyj + Lzk
R = Rxi + Ryj + Rzk
cosα = (RxLx + RyLy + RzLz)/(L0*R)
|
Вопрос 46:
Трение скольжения. Законы Кулона. Угол и конус трения.
Между движущимися телами в плоскости их соприкосновения возникает сила трения скольжения. Обусловлено это прежде всего шероховатостью соприкасающихся поверхностей и наличием сцепления у прижатых тел.
В инженерных расчетах обычно пользуются установленными опытным путем закономерностями, которые с некоторой степенью точности отражают действие силы трения. Эти закономерности называют законами трения скольжения (Кулона). Их можно сформулировать следующим образом:
1)Сила трения скольжения лежит в интервале 0FтрFмах;
2) Сила трения скольжения не зависит от площади соприкасающихся тел, а зависит лишь от силы давления этого тела на поверхность
3)Сила тр.скольженияопр-ся по ф-ле: Fтр=fN, N-сила реакции опоры =Р, f-коэф-т трения скольжения
4)Коэф-т трения скольжения завис.от шероховатостей пов-тей трущихся тел, от температуры, от физич.состояния материала.
Тангенс угла трения равняется коэффициенту трения. Полная реакция неидеальной связи при равновесии имеет направление в пределах угла трения.
Конус трения.
Рассмотрим равновесие невесомого тела на горизонтальной шероховатой плоскости под действием наклонной силы F1, стремящейся его сдвинуть.
П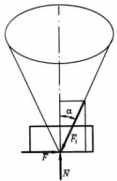 оворачивая вокруг вертикали вектор силы F1 и сохраняя при этом предельное равновесие, опишем конус, называемый конусом трения. Если свойства соприкасающихся поверхностей во всех направлениях одинаковы, то угол а будет постоянным, а конус трения круговым. Конус трения обладает тем замечательным свойством, что если действующая на тело сила находится внутри него, то тело всегда будет находиться в равновесии. Этим объясняются известные явления заклинивания, или самоторможения тел. оворачивая вокруг вертикали вектор силы F1 и сохраняя при этом предельное равновесие, опишем конус, называемый конусом трения. Если свойства соприкасающихся поверхностей во всех направлениях одинаковы, то угол а будет постоянным, а конус трения круговым. Конус трения обладает тем замечательным свойством, что если действующая на тело сила находится внутри него, то тело всегда будет находиться в равновесии. Этим объясняются известные явления заклинивания, или самоторможения тел.
Тело будет сдвинуто только тогда, когда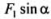 >Fmax = >Fmax =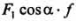 . Предельному случаю равновесия соответствует такой угол . Предельному случаю равновесия соответствует такой угол
наклона a, при котором выполняется равенство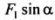 = =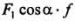 , или tgα = f. Если tgα<=f, то как бы не возрастала сила F1, тело сдвинуть с места невозможно. Возрастающей сдвигающей силе , или tgα = f. Если tgα<=f, то как бы не возрастала сила F1, тело сдвинуть с места невозможно. Возрастающей сдвигающей силе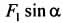 будет противостоять пропорционально ей увеличивающаяся сила трения будет противостоять пропорционально ей увеличивающаяся сила трения . .
|
Вопрос 47:
Трение качения. Коэффициент трения качения.
Круглое тело вдавливается в опорную поверхность (дуга CD). Трение качения – сопротивление, возникающее при качении одного тела по поверхности другого. Полная реакция N’ опорной поверхности препятствует качению.
Нам нужен момент сопротивления качению => заменим N’ и представим в виде Fтр. и N, приложенных в точкеВ, смещенной от центра на δ. Условия равновесия: N=P, F=Q. QmaxR=δN. Mтр.max=δ∙N. Момент сопротивления качению 0кк.max (не зависит от радиуса). Коэффициент трения качения δ при предельном состоянии равновесия (при Qmax) N (сила нормального давления) отстает на δ от вертикального радиуса. δ не зависит от материала, из которого сделано тело. Определяется экспериментально.

|
Вопрос 48:
Центр системы параллельных сил. Формула для радиус-вектора и координат центра системы параллельных сил.
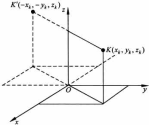
На каждую частицу тела, находящегося вблизи поверхности Земли, действует направленная вертикально вниз сила, которая называется силой тяжести. Силы тяжести каждой частицы тела, строго говоря, направлены по радиусам к центру Земли и не являются параллельными. Но для тел, размеры которых малы по сравнению с размерами Земли, непараллельность настолько незначительна, что в расчетах с большой точностью силы тяжести их частиц можно считать параллельными, сохраняющими свои значения, точки приложения и параллельность при любых поворотах тела. Поэтому, обозначив силу тяжести частицы через Рк , можно, согласно формулам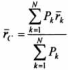 и и 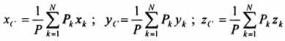 , найти точку С, которая неизменно связана с телом и называется центром системы параллельных сил тяжести. , найти точку С, которая неизменно связана с телом и называется центром системы параллельных сил тяжести.
Таким образом, центром тяжести твердого тела называется центр системы параллельных сил тяжести частиц данного тела.
Дано :F1 || F2 .
R=F1+F2. MC(R)=MC(F1)+MC(F2)=0
F1∙CA1=F2∙CA2. ПовернемF1 и F2 на угол α, при этом Rповернется тоже на угол α. С – центр параллельных сил.
То же самое, если сил несколько и не по одной прямой. R=∑Fi, R||Fi (точка С принадлежит R) MO(R)=∑MO(Fi), rC×R=∑(ri×Fi).
Введем единичный вектор eFk=Fk∙eR=∑Fk∙e.
rC×∑Fi∙e=∑ri×(Fi∙e). ∑FirC×e=∑Firi×e.
(∑FirC-∑Firi)×e=0
rC=∑Firi/∑Fi.
Координаты центра системы параллельных сил:
XC=∑Fixi/R; YC=∑Fiyi/R;
ZC=∑Fizi/r
|
Вопрос 49:
Центр тяжести тела. Методы нахождения центра тяжести.
Центр тяжести – центр системы параллельных сил тяжести частиц тела. Его радиус-вектор rC=∑Piri/P.
XC=∑Pixi/P; Yc=∑Piyi/P; ZC=∑Pizi/P
Вес тела P=∑Pi, Pi – сила тяжести частицы.
Методы определения координат центра тяжести тела.
Свойства симметрии: если тело имеет плоскость, ось или центр симметрии, то центр тяжести лежит на них.
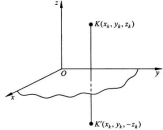 
Разбиение: Если известны центры тяжести отдельных частей тела, то
rC=(V1rC1+V2rC2+…+VnrCn)/V
Отрицательные массы:
rC=VсплrC-V1rC1-…-VnrCn, где Vk, rCk – объемы и радиус-векторы пустот тела.
Интегрирование: если тело нельзя разбить)
XC=(∫xdV)/V, YC=(∫ydV)/V,
ZC=(∫zdV)/V
К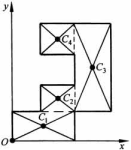 огда тело нельзя разбить на составные части, центры тяжести которых известны, используют метод интегрирования, являющийся универсальным. огда тело нельзя разбить на составные части, центры тяжести которых известны, используют метод интегрирования, являющийся универсальным.
|
Вопрос **:
Способы определения углового ускорения при плоском движении твердого тела.
Если задана зависимость ула поворота плоского тела от времени φ=φ(t), то ε=φ׳׳(t);
Если известна зависимость угловой скорости от времени ω=ω(t), то, так как ω=vτ/R, то ε=ω׳(t)=d/dt(vτ/R)=1/R∙dvτ/dt= aτ/R.
Из условия задачи.
Например,
Y
 
B
C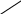


AX
Если известны по модулю aA и (aBA)n, то, проецируя векторное равенство aB=aA+(aBA)τ+(aBA)n на ось Ох, получим:
εAB∙AB∙sinφ=aA+(ωAB)²∙AB∙cosφ
|
Вопрос ***:
Полная и локальная производные вектора. Формула Бура.
Пусть задан вектор b(t)=bxi+byj +bzk в подвижной системе отсчета. Орты i, j, k не меняются в подвижной системе отсчета. Поэтому локальная производная db/dt=dbx/dt∙i+dby/dt∙j+dbz/dt∙k, а полная производная с учетом изменения также ортов i, j, kпримет вид: db/dt= dbx/dt∙i+dby/dt∙j+dbz/dt∙k+bxdi/dt+ bzdj/dt+ bzdk/dt.= db/dt+ω×(bxi+ byj+bzk)= db/dt+ω×b.
db/dt=db/dt+ω×b – формула Бура.
Частные случаи:
А) ω=0db/dt= db;
Б) Если вектор b не меняется в подвижной системе отсчета, то db/dt=ω×b;
В) Если b все время параллелен вектору
|
|
 Скачать 1.21 Mb.
Скачать 1.21 Mb.