практическая работа. пр 1 11С. Практическая работа 1 Определение равнодействующей системы сил
 Скачать 460.46 Kb. Скачать 460.46 Kb.
|
|
Практическая работа №1 Определение равнодействующей системы сил. Определить равнодействующую плоской системы сходящихся сил аналитическим и геометрическим способами (рис. П1.1). Дано: 1. Определить равнодействующую аналитическим способом (рис. П1.1a). 2. Определить равнодействующую графическим способом. 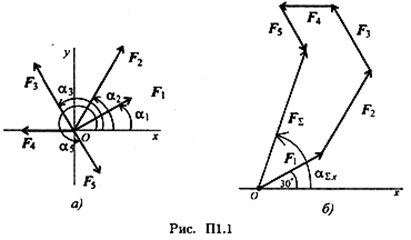  С помощью транспортира в масштабе 2 мм = 1 кН строим многоугольник сил (рис. П1.1б). Измерением определяем модуль равнодействующей силы и угол наклона ее к оси Ох. Результаты расчетов не должны отличаться более чем на 5%: Расчетно-графическая работа №1. Определение равнодействующей плоской системы сходящихся сил аналитическим и геометрическим способами
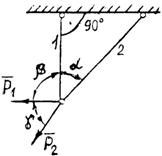
Задание 1. Используя схему рис. П1.1а, определить равнодействующую системы сил геометрическим способом Практическая работа № 2. Определение усилий в стержнях стержневой конструкции. Тема: Статика. Плоская система сходящихся сил. Цель работы: Научится определять усилия в стержнях конструкции аналитическим методом. Задание: Определить усилия в стержнях заданной конструкции аналитическим способом. Схему выбрать в соответствии с номером студента по списку журнала. Порядок выполнения: 1. Изобразить заданную схему в соответствии с вариантом. 2. Выделить материальную точку, к которой приложена внешняя сила. 3. Определить тип связей, удерживающих точку. 4. Отбросить связи, заменить их действие силами реакции. 5. Составить расчетную схему, выделив точку, находящуюся в равновесии. Приложить к ней все действующие силы. 6. Выбрать оси координат. 7. Записать уравнения равновесия: 8. Из уравнений равновесия найти величину сил реакции. 9. Записать величину усилий в стержнях. 10. Вычертить многоугольник сил, приложенных к точке. 11 .Вывод. Пример 1. Стержни АС и ВС (рис. 1,а) соединены между собой шарниром С, а с вертикальной стеной — посредством шарниров А и В. В шарнире С приложена сила F = 1260 Н. Требуется определить реакции N1 и N2 стержней действующие на шарнир С, если 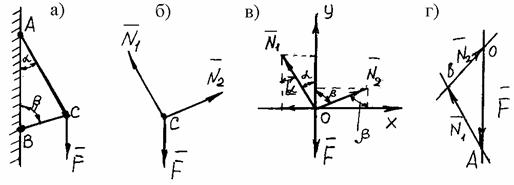 Рис. 1 Решение. Рассматриваем равновесие точки С, которая считается несвободной, так как на нее наложены связи в виде стержней АС и ВС. Освобождаем точку С от связей и заменяем их силами реакций связей, считая, что стержень АС растягивается, а стержень ВС сжимается под действием силы F. Обозначим реакцию стержня АС через N1, а реакцию стержня ВС через N2. В итоге точка С становится свободной, находясь под действием плоской системы трех сходящихся сил: активной силы F и сил реакций N1 и N2 (рис. 1, б). Приняв точку О за начало координат, перенесем силы F, N1 и N2 параллельно самим себе в эту точку (рис. 1, в) и составляем уравнения проекций сил на оси координат: или и Умножим уравнение (1) на После сложения уравнений (3) и (4) получим откуда 2N2 = F или Графический метод. Для решения задачи этим методом выбираем масштаб силы F (например, 10 Н = 1 мм) и строим замкнутый треугольник сил (рис. 1, г). Из произвольной точки О проводим прямую, параллельную вектору F, и откладываем на этой прямой в выбранном масштабе вектор Ответ: N1 = 1089,9 H; N2 = 630 H Пример 2. Два жестких стержня АВ и АС имеют общую шарнирную точку А и шарнирные опоры В и С (рис. 1, а). Сила F= 500 Н приложена к шарнирному валику в точке А. Стержни АВ и АС образуют углы 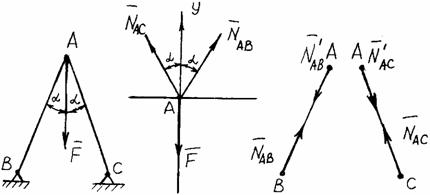 а) б) в) Рис. 1 Решение. Сила F приложена в точке А, которая находится в равновесии под действием силы F и реакции стержней АВ и АС. Реакции стержней направлены вдоль их осей. Рассмотрим равновесие точки А. Отбросив связи точки А и заменив их реакциями стержней АВ и АС (рис. 1, б), получим систему сходящихся сил. Из точки А проведём координатные оси. Ось Х направим перпендикулярно силе F. Составим уравнение равновесия (сумма проекций всех сил на ось Х равна нулю): откуда NAB = NAC. Сумма проекций всех сил на ось Y также равна нулю: откуда В данном примере силы NAC и NAB получились со знаком «плюс» (+), следовательно, действительное направление сил совпадает с тем, которое предполагалось при составлении уравнения. Если сила получится со знаком «минус» (-), то это значит, что ее действительное направление противоположно тому, которое было намечено при составлении уравнений равновесия. Мы определили величину, а также направление реакций стержней, приложенных к точке A. К верхним концам стержней приложены такие же по величине силы, но противоположно направленные. К нижним концам стержней приложены силы реакции опор В и С, равные по величине силам, приложенным к верхним концам, и направленные им навстречу (рис. 1, в). Следовательно, оба стержня сжимаются силами NAC = NAB = 288,7 H. Ответ: NAC = NAB = 288,7 H. 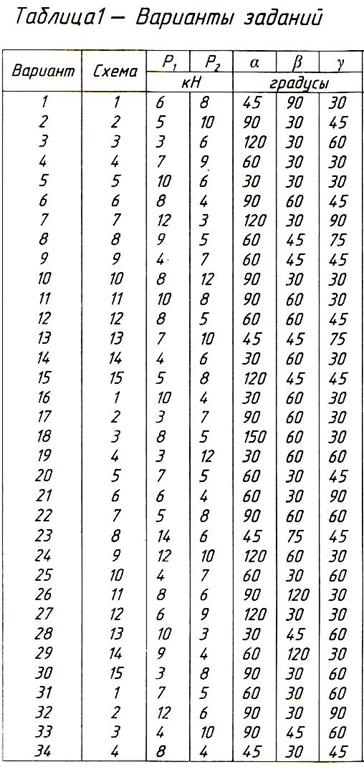 Задания к практической работе № 2
Практическая работа № 3 Определение реакций опор балки на двух опорах. Тема: Статика. Плоская система произвольно расположенных сил. Цель работы: Научится определять реакции опор балки установленной на двух опорах. Задание: Определить реакции опор балки на двух опорах. Схему выбрать в соответствии с номером студента по списку в журнале. Принять: Порядок выполнения. 1. Изобразить схему в соответствии с вариантом. 2. Заменить распределенную нагрузку ее равнодействующей Q=q·l. Приложить равнодействующую к балке в центре тяжести соответствующего прямоугольника. 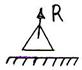 3. Заменить опоры их реакциями. Реакцию шарнирно-подвижной опоры направить перпендикулярно к опорной поверхности. 3. Заменить опоры их реакциями. Реакцию шарнирно-подвижной опоры направить перпендикулярно к опорной поверхности.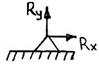 Реакцию шарнирно-подвижной опоры разложить на две составляющие, направленные по осям координат. Реакцию шарнирно-подвижной опоры разложить на две составляющие, направленные по осям координат.4. Составить расчетную схему балки. 5. Выбрать оси координат и центры моментов. 6. Составить уравнение равновесия: 7. Из уравнений равновесия найти неизвестные реакции опор. 8. Провести проверку правильности решения, составив уравнения 9. Записать ответы. 10. Вывод. Пример.Определить реакции опор горизонтальной балки от заданной нагрузки. Дано: Схема балки (рис. 1). P = 20 кН, G = 10 кН, М = 4 кНм, q = 2 кН/м, a=2 м, b=3 м, ___________________________________ Определить реакции опор в точках А и В. 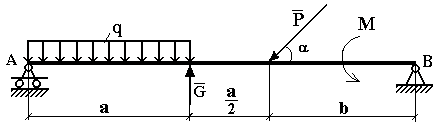 Рис. 1 Решение: Рассмотрим равновесие балки АВ (рис. 2). К балке приложена уравновешенная система сил, состоящая из активных сил и сил реакции. Активные (заданные) силы: Величина Линия действия силы Силы реакции (неизвестные силы): Реакция Расчетная схема 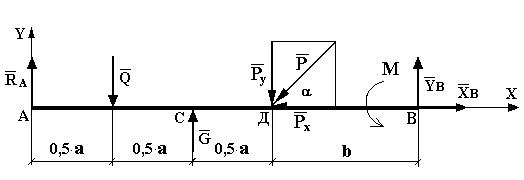 Рис. 2 Для полученной плоской произвольной системы сил можно составить три уравнения равновесия: Задача является статически определимой, так как число неизвестных сил ( Поместим систему координат XY в точку А, ось AX направим вдоль балки. За центр моментов всех сил выберем точку В. Составим уравнения равновесия: 1) 2) 3) Решая систему уравнений, найдем 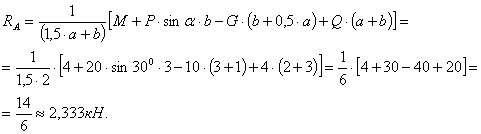 Определив В целях проверки составим уравнение Если в результате подстановки в правую часть этого равенства данных задачи и найденных сил реакций получим нуль, то задача решена - верно. 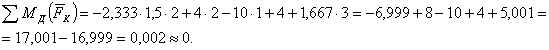 Реакции найдены верно. Неточность объясняется округлением при вычислении Ответ: Задания к практической работе № 2
|

 1
1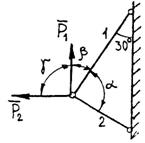 2
2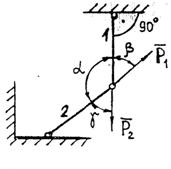 3
3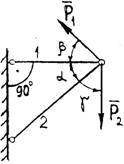 4
4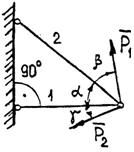 5
5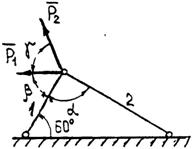 6
6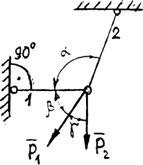 7
7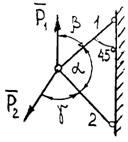 8
8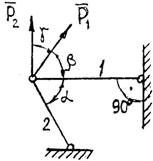 9
9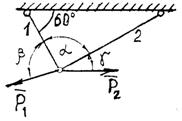 10
10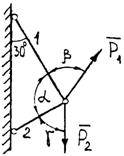 11
11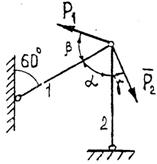 12
12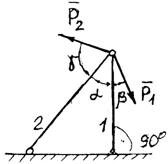 13
13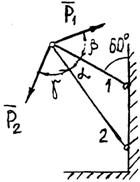 14
14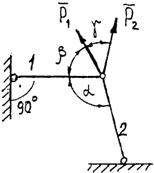 15
15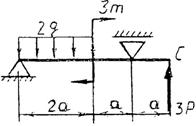 1
1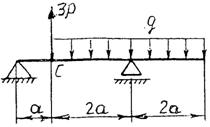 2
2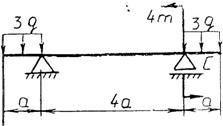 3
3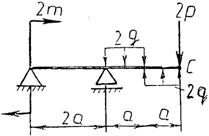 4
4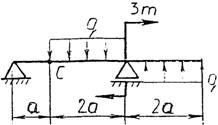 5
5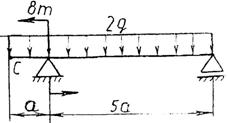 6
6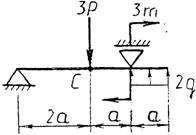 7
7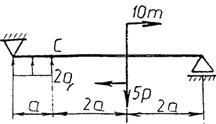 8
8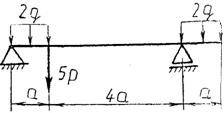 9
9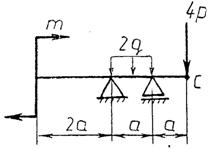 10
10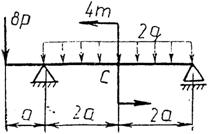 11
11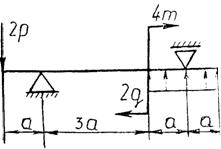 12
12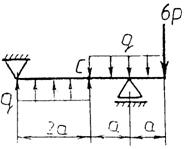 13
13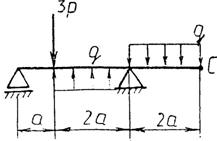 14
14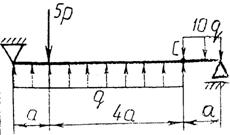 15
15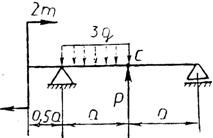 16
16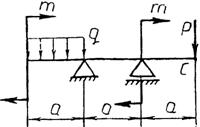 17
17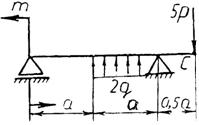 18
18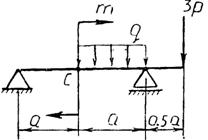 19
19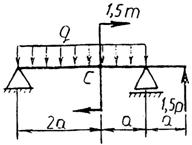 20
20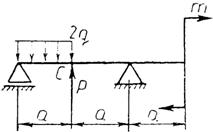 21
21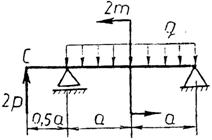 22
22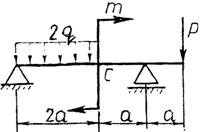 23
23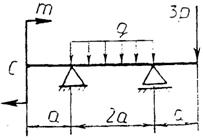 24
24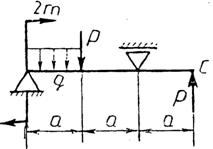 25
25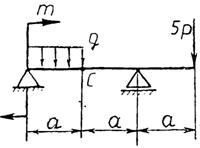 26
26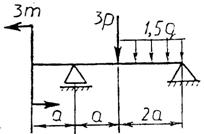 27
27