|
|
Учебное пособие. Содержание. В 4 5 6 10 13 14 14 16 20 25 26 28 29 30 31 34 36 37

a)
Учебный военный центр
Основные элементы вычислений прямоугольных
координат, дирекционных углов и дальностей.
Учебное пособие.
Содержание.
В
4
5
6
10
13
14
14
16
20
25
26
28
29
30
31
34
36
37
38
39
40
41
42
43
44
45
45
46
ведение.
Основные правила вычислений.
Мера измерения углов. Перевод градусной меры в деления угломера и обратно.
Зависимость между линейной и угловой величинами.
Азимуты и дирекционный угол.
Прямой и обратный дирекционный угол.
Определение величины горизонтального угла по дирекционным углам направлений, составляющих этот угол, и наоборот.
Переход от истинного азимута к дирекционному углу. Определение сближения меридианов.
Переход от магнитного азимута к дирекционному углу и обратно. Определение поправки буссоли по данным карты.
Тригонометрические функции острого угла.
Решение треугольника.
Определение превышений и абсолютных высот.
Приведение наклонных расстояний к горизонту.
Определение расстояний засечкой с помощью базы.
Прямая геодезическая задача.
Обратная геодезическая задача.
Заключение.
Приложения:
Таблица перевода градусов и минут в деления угломера.
Таблица перевода делений угломера в градусы и минуты.
График для определения сближения меридианов.
График и таблица для определения поправки .
Таблица натуральных значений тригонометрических функций
sin и cos (в градусной мере).
Таблица натуральных значений тригонометрических функций
sin и cos (в делениях угломера).
Таблица определения расстояний засечкой с помощью базы.
Таблица поправки .
Таблица поправок Д за приведение наклонных дальностей к горизонту (м).
Таблица для расчета топографической дальности и дирекционного угла цели (таблица Кравченко).
ВВЕДЕНИЕ.
Топогеодезическая привязка элементов боевого порядка артиллерийских подразделений слагается из полевых измерений и обработки материалов полевых измерений. Обработка результатов полевых измерений может выполняться графическим методом или путем вычислений (аналитическим методом).
Успешное и быстрое получение результата привязки и точность этого результата, во многом зависит от качества графических и вычислительных работ. Небрежное отношение к вычислениям, несоблюдение основных правил их выполнения, могут загубить весь результат быстро и точно сделанных полевых измерений.
Аналитический метод обработки результатов полевых измерений наиболее точный и представляет собой числовое решение некоторых типовых задач, по основным формулам геодезии, в которые входят тригонометрические функции. Вычисления, производимые по основным формулам геодезии, называют основными элементами геодезических вычислений, которые включают: определение величины горизонтального угла по дирекционным углам направлений, составляющий этот угол; решение треугольника; определение сближения меридианов; переход от истинного или магнитного азимута к дирекционному углу и обратно; определение превышений; решение прямой и обратной геодезической задачи.
Вычисления можно выполнять по таблицам (логарифмов, приращений координат, натуральных значений тригонометрических функций и др.), с помощью логарифмической линейки, СТМ, инженерного микрокалькулятора или ЭВМ. Основные правила вычислений приведены в настоящем пособии.
В данном пособии дается понятие об артиллерийской мере измерения углов, а также предлагаются некоторые рациональные приемы и правила расчета прямоугольных координат, дирекционных углов, дальностей, и некоторых других величин с помощью таблиц, графиков и микрокалькулятора. Наличие большого количества рисунков, типовых примеров и задач должно способствовать лучшему усвоению изложенного на лекциях и групповых занятиях материала.
Пособие содержит много приложений в виде таблиц и графиков, которые окажу помощь в решении задач на практических занятиях и при подготовке к зачетам и экзаменам в процессе обучения. Некоторые из таблиц и графиков разработаны на кафедре и печатаются впервые с расчетом на то, что они облегчат процесс обработки результатов полевых измерений, и найдут свое практическое применение.
Основные правила вычислений.
Для быстрого и, по возможности, безошибочного выполнения вычислений, необходимо строжайшим образом соблюдать следующие правила:
Все исходные величины, на которых основаны дальнейшие вычисления (координаты точек, угловые и линейные величины) должны тщательно проверяться.
Вычисления следует проводить по возможности на бланках. При ведении записей необходимо соблюдать определенную последовательность.
Цифры необходимо писать четко, разборчиво и без исправлений. Числа следует располагать так, чтобы цифры одного и того же разряда находились строго одна над другой.
Если при записи числа, полученного в результате вычислений, возникает сомнение в его правильности, то проверка данного числа обязательна. Лучше лишний раз проверить результат промежуточных вычислений, чем искать причину ошибки окончательного результата.
В ходе вычислений необходимо контролировать полученный результат. Если искомый результат может быть получен по разным формулам, то часть из них должны быть использованы в качестве контрольных.
Перед производством вычислений должны быть подготовлены и проверены вычислительные средства. Вычисления производить с практически необходимой точностью.
При вычислениях некоторые величины могут иметь знак «+» или «–». На знаки необходимо обращать особое внимание, так как пренебрежение знаками приводит к грубейшим ошибкам и полному искажению конечного результата. Чтобы не допустить ошибки, необходимо обязательно обозначать не только знак «–», но и знак «+».
В ходе вычислений необходимо придерживаться общепринятых правил округления чисел. Если в отбрасываемой части числа цифра высшего разряда меньше "5", то последняя сохраняемая цифра остается без изменения, если же она больше "5", то последняя сохраняемая цифра увеличивается на единицу.
Необходимо помнить, что отыскание ошибок, допущенных при вычислениях и обнаруженных при контроле конечного результата, является весьма трудной задачей, часто отнимающей больше времени, чем сами вычисления. Поэтому, никогда не следует экономить время на вычисления за счет несоблюдения приведенных выше правил.
Мера измерения углов. Перевод градусной меры
в деления угломера и обратно.
При топогеодезических работах на местности измерение углов может вестись, в зависимости от прибора, в градусной мере или в делениях угломера. А за единицу меры угловых величин в артиллерии принято деление угломера. Поэтому, для уверенной работы на топогеодезических приборах, стоящих на вооружении в артиллерийских частях, для перехода от величины угла, выраженной в градусной мере к делениям угломера и наоборот необходимо знать меру измерения углов, применяемую в артиллерии.
Градусная мера. Основная единица – градус (1/90 прямого угла):
1 = 60; 1 =60
Пример записи угла:
= 5412 48 (в градусах, минутах и секундах);
= 5412,8 (в градусах, минутах и десятичных долях минут);
= 5413 (в градусах и минутах);
= 54,2133…( в градусах и десятичных долях градусов);
Артиллерийская мера. Основная единица – деление угломера (тысячная) – центральный угол, стягиваемый дугой, равной 1/6000 части длины окружности. Длина дуги в одно деление угломера равна, примерно, 1/1000 радиуса, отсюда и название – тысячная, (рис. 1.).
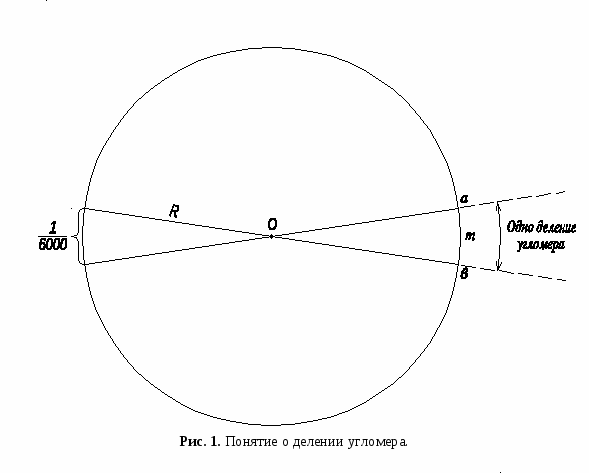
Чтобы представить этот угол, возьмем булавку и закрепим ею две нити, длина которых 1м (1000 мм) каждая. Сведем эти две нити на расстояние 1мм друг от друга. Образовавшийся угол будет равен одной тысячной (0-01).
Если окружность радиуса R разделить на 6000 равных частей и точки деления соединить с центром окружности, то получим 6000 центральных углов (рис. 1).
Возьмем длину дуги атв, соответствующей одному делению угломера, в долях радиусаR:
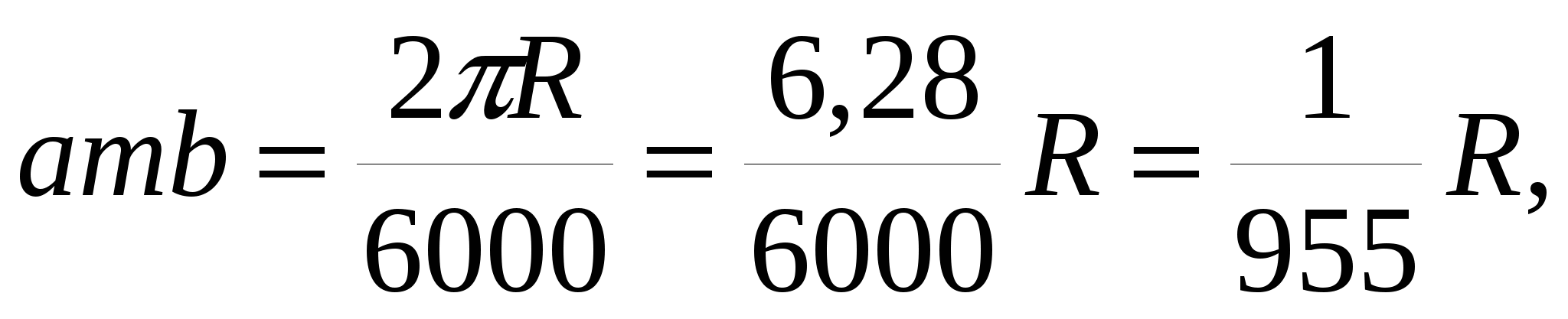 (1) (1)
т. е. 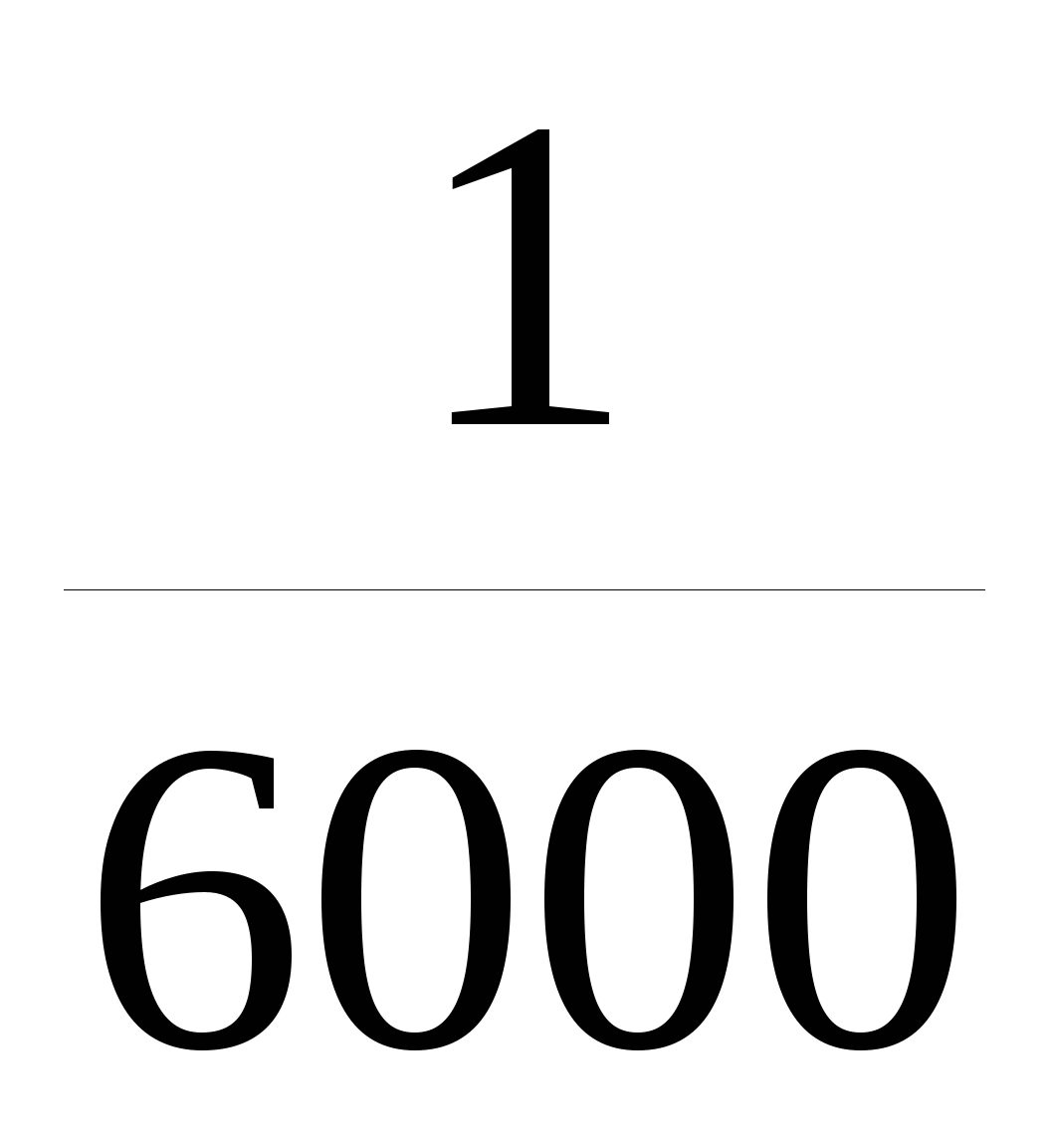 дуги окружности равна дуги окружности равна  данной окружности. При практических расчетах удобно считать, что данной окружности. При практических расчетах удобно считать, что 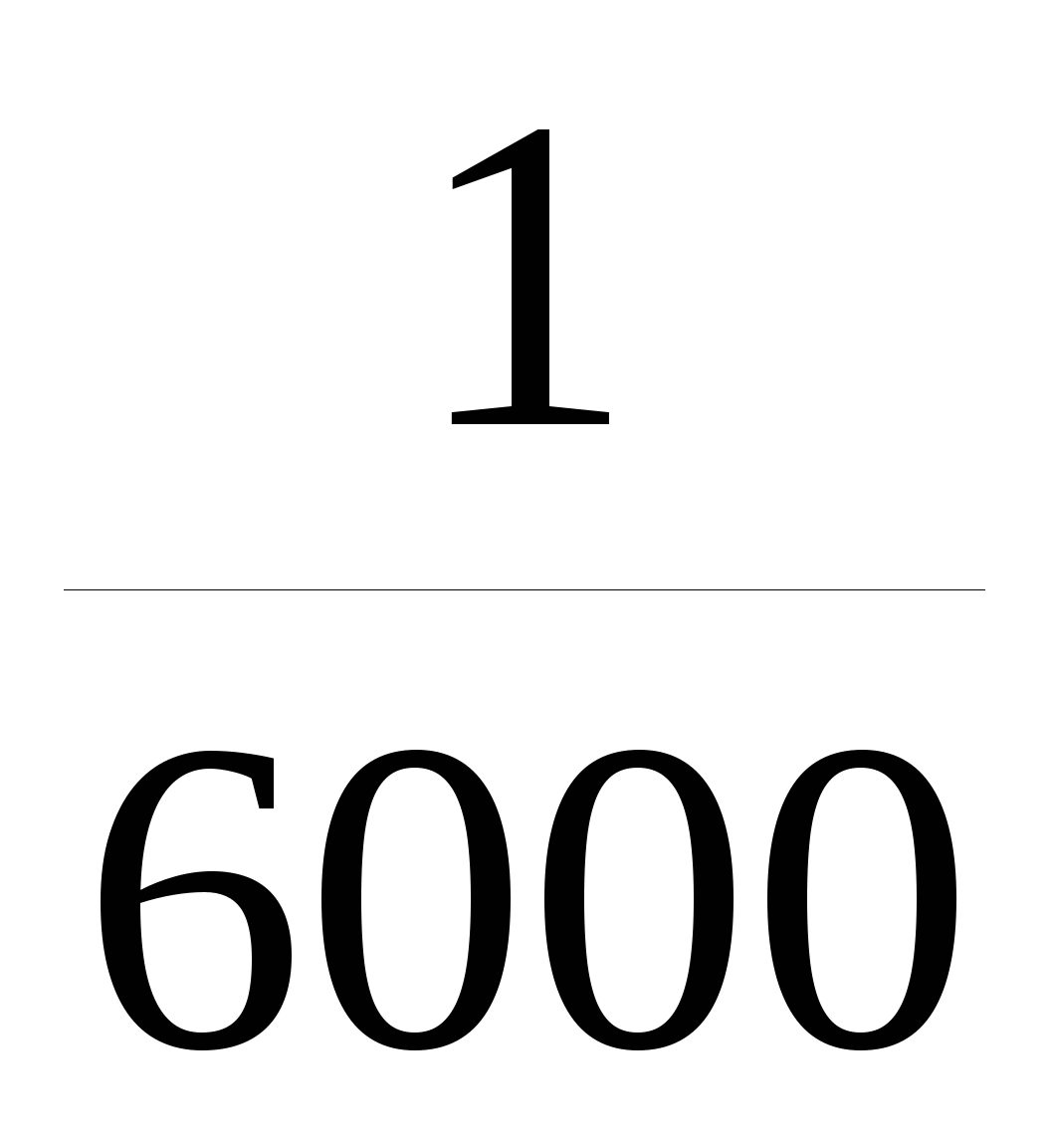 дуги окружности равна дуги окружности равна 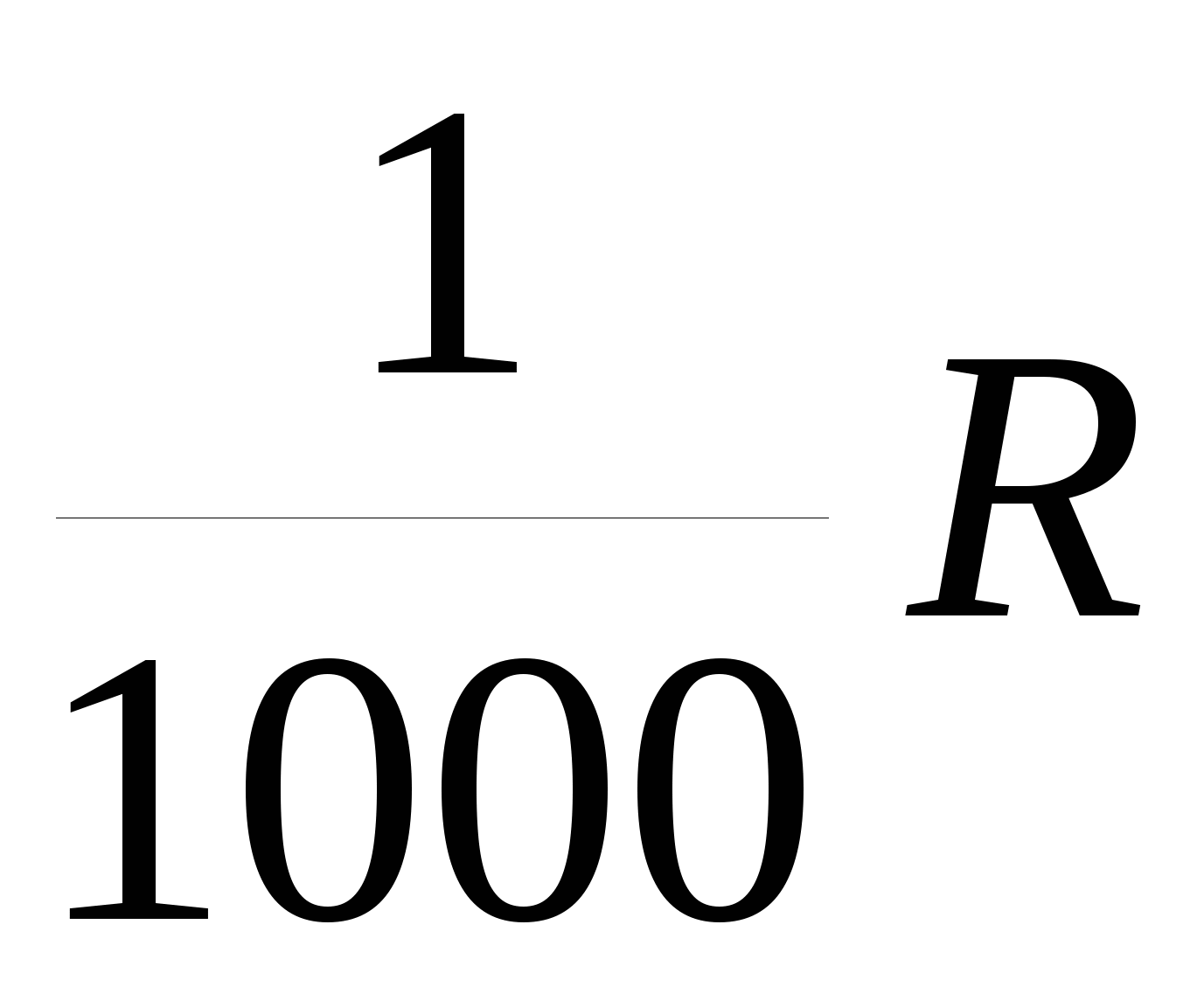 данной окружности, но при этом допускается некоторая ошибка (Е): данной окружности, но при этом допускается некоторая ошибка (Е):
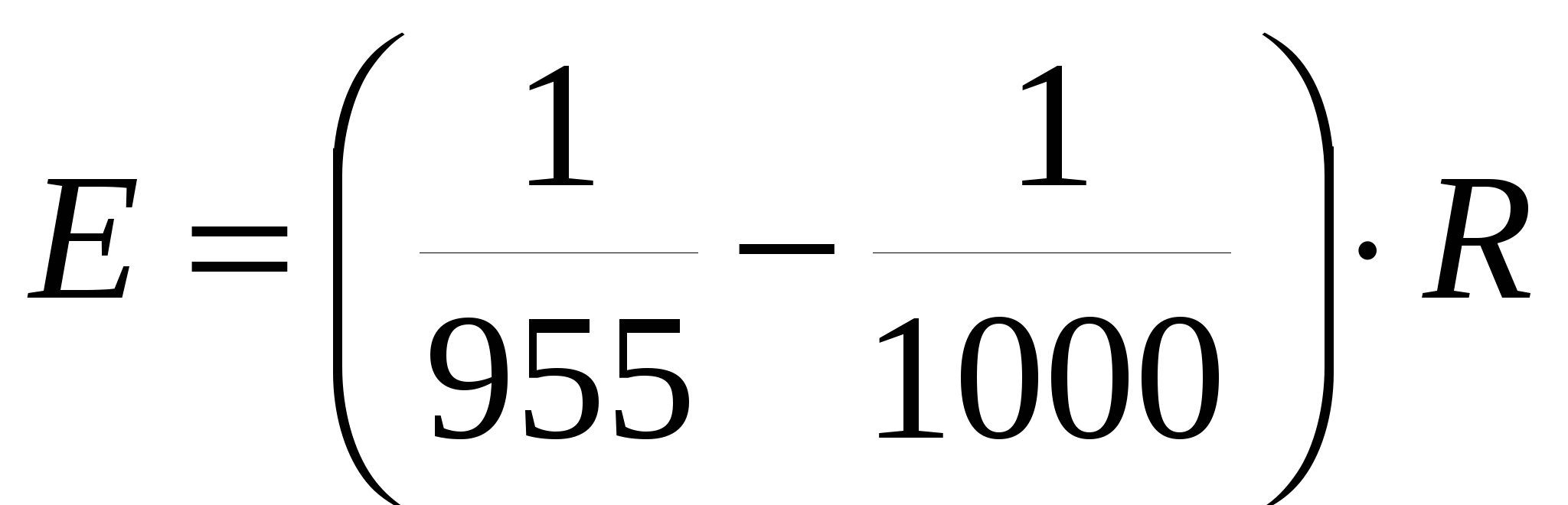 (2) (2)
Таким образом, окружность содержит 6000 делений угломера (дел. угл.) или 6000 "тысячных" радиуса или просто "тысячных".
В практике иногда применяют термины: "малое деление угломера", "большое деление угломера".
Малым делением угломера называют одно деление угломера – одну "тысячную дальности".
Большим делением угломера называют 100 малых делений угломера (100 "тысячных" , 1-00).
При измерении углов в делениях угломера (тысячных) принято записывать через черточку (дефис) большие и малые деления и читать раздельно:
-
Угол, тыс.
|
Запись
|
Читается
|
4379
|
43-79
|
Сорок три семьдесят девять
|
1500
|
15-00
|
Пятнадцать, ноль
|
1250
|
12-50
|
Двенадцать, пятьдесят
|
251
|
2-51
|
Два, пятьдесят один
|
35
|
0-35
|
Ноль, тридцать пять
|
1
|
0-01
|
Ноль, ноль один
|
В градусной мере одна тысячная (или одно деление угломера) равна:
0-01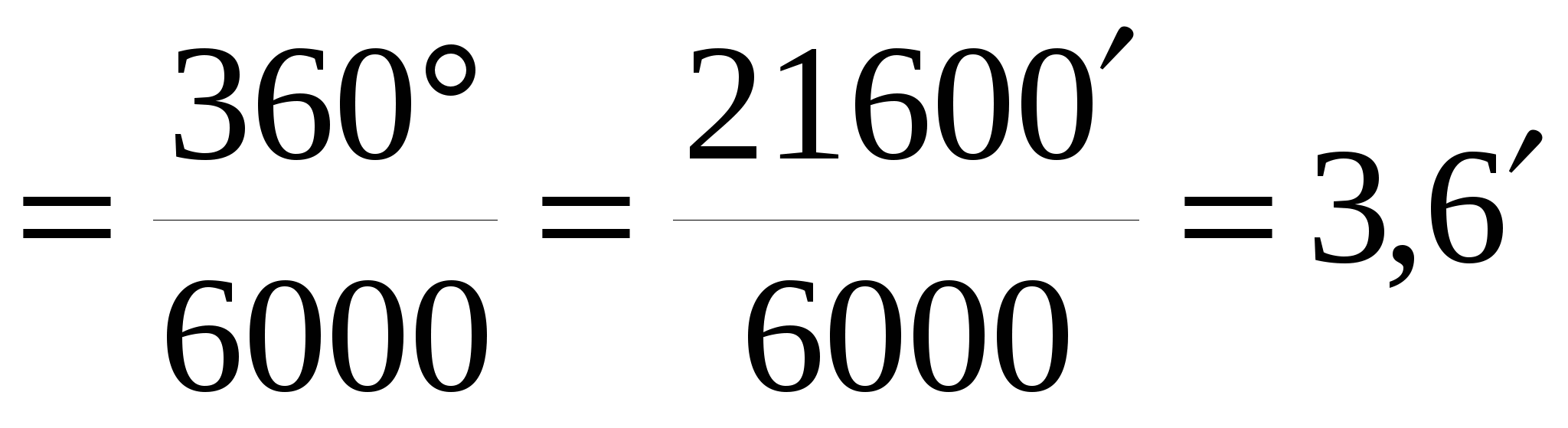
Одно большое деление угломера равно: 1-00 =
Один градус равен:  0-16,7; 0-16,7;
10 = 0-02,8;
1 = 0-00,3;
Данными соотношениями пользуются для перевода величины углов, выраженных в делениях угломера, в величины, выраженные в градусах и минутах (и наоборот).
Перевод градусной меры в деления угломера.
Большинство артиллерийских задач связано с вычислениями углов и дальностей. При этом углы в артиллерии обычно выражаются в делениях угломера. Однако выпускаемые нашей промышленностью и импортные инженерные микрокалькуляторы производят математические операции с углами, выраженными в градусах (DEG), градах (GRAD) и радианах (RAD). Грады и радианы в артиллерии при вычислениях практически не применяются. Поэтому при решении многих артиллерийских задач приходится делать перевод углов, заданных в делениях угломера, в градусную меру и наоборот.
Перевод градусной меры в деления угломера производится по таблице перевода градусов и минут в деления угломера (Приложение 1). Перевод делений угломера в градусную меру производится по таблице (Приложение 2).
Пример 1. Преобразовать дирекционный угол с градусной меры = 21337 в деления угломера:
Р е ш е н и е: Из таблицы 180= 30-00,0
33 = 5-50,0
37 = 0-10,3
––––––––––––––
21337= 35-60,3
Пример 2. Преобразовать дирекционный угол с делений угломера в градусную меру = 35-60,3
Р е ш е н и е: Из таблицы 35-00 = 210
0-60 = 336
0-00,3 3,6 1
––––––––––––––
35-60,3 = 21337
Перевод градусной меры в деления угломера и обратно можно также выполнить с помощью микрокалькулятора. Для перевода угла , заданного в делениях угломера, в градусную меру с помощью микрокалькулятора применяется коэффициент КГ = 6. Значение этого коэффициента определено на основании известного в артиллерии соотношения:
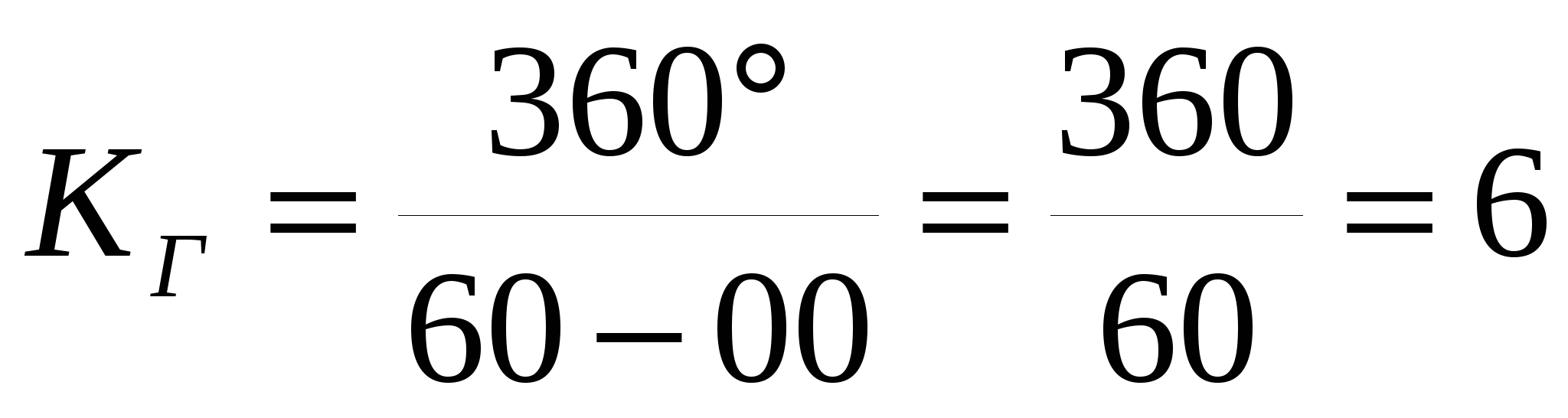 . .
Для получения угла в градусной мере угол, введенный в микрокалькулятор в делениях угломера, отделяя при этом большие деления от малых делений запятой, нужно умножить на число 6, т. е.
= 6 (3)
Пример 3. Дирекционный угол цели ц= 6-73. определить значение этого угла в градусах.
Р е ш е н и е. 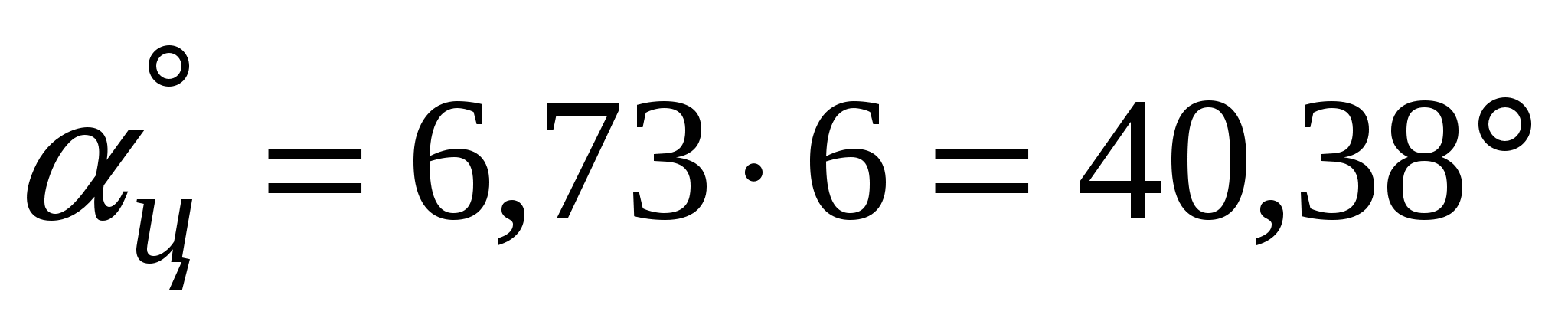 . .
Обратная задача – перевод угла из градусной меры в деления угломера – решается с помощью этого же коэффициента КГ = 6 по формуле:
= 6. (4)
Пример 4. При определении топографических данных по цели с помощью микрокалькулятора получен топографический дирекционный угол цели в градусах определить значение этого угла в делениях угломера. определить значение этого угла в делениях угломера.
Р е ш е н и е. 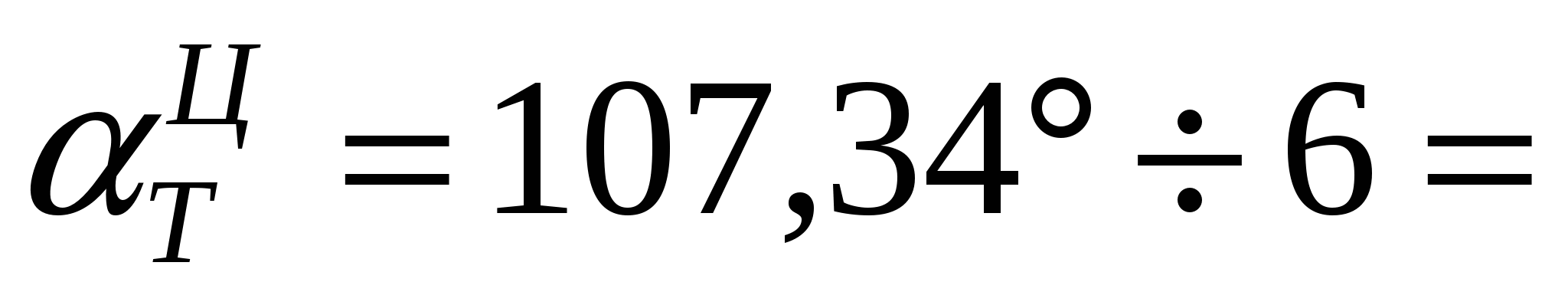 17,89 = 17-89. 17,89 = 17-89.
Переход от угловых минут и секунд к десятичным долям градуса и наоборот.
Если угол задан в градусах, минутах и секундах, то прежде чем перейти к делениям угломера необходимо сначала перевести его в градусы и десятичные доли градуса. Переход от угловых минут и секунд к десятичным долям градуса производится по формуле:
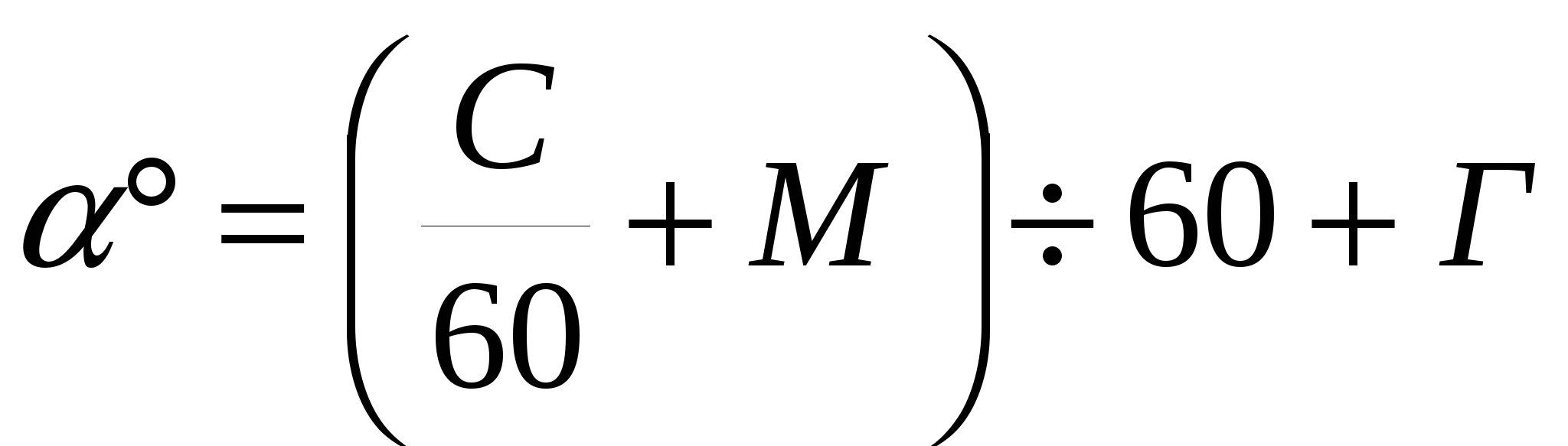 , (5) , (5)
где – угол в градусах и десятичных долях градуса;
С – число секунд;
М – число минут;
Г – число градусов.
Пример 5. Используя формулу (5), перевычислить угол = 171524, выраженный в градусах минутах и секундах в десятичные доли градуса.
Р е ш е н и е. 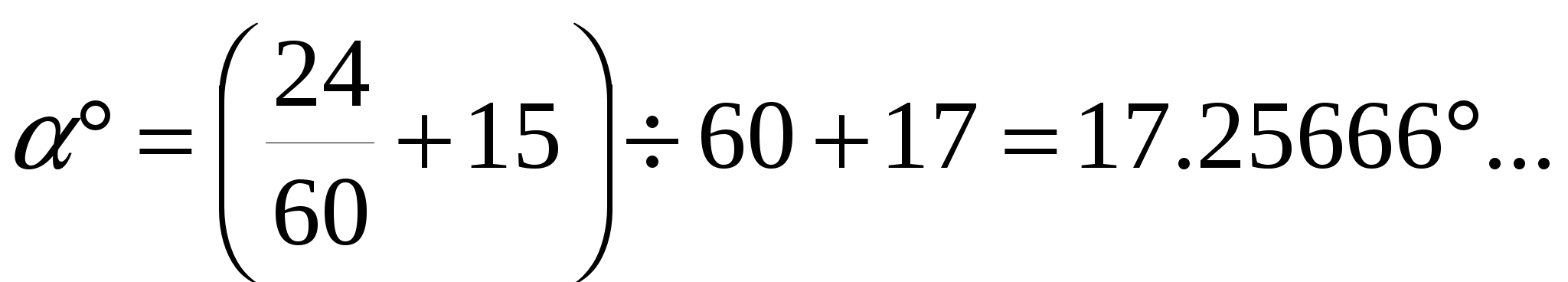
На многих недорогих микрокалькуляторах импортного производства имеется кнопка перевода углов заданных в градусах, минутах и секундах в градусы и десятичные доли градуса.
 
или – кнопка перевода в градусы и десятичные доли градуса.
С помощью этой кнопки перевод значительно упрощается.
Для перевода необходимо набрать на калькуляторе значение угла в виде: градусы, запятая минуты и секунды без разделения (17,1524), а затем нажать кнопку перевода. На калькуляторе высветится угол в градусах и десятичных долях градуса (17,25666…).
Переход от градусов и десятичных долей градуса к градусам минутам и секундам выполняется в следующей последовательности:
переводят десятичные доли градуса в минуты и десятичные доли минуты по формуле:
М= (–Г) 60; (6)
переводят десятичные доли минуты в секунды по формуле:
С = (М– М) 60; (7)
где М– число минут и десятых долей минуты;
С– число секунд;
Пример 6. Перевычислить дирекционный угол = 17,25666 заданный в градусах и десятичных долях градуса в градусы, минуты и секунды:
Р е ш е н и е: М= (17,25666– 17) 60 = 15,3999…;
С = (15,39999 – 15) 60 = 23,9999…= 24;
Следовательно, угол в градусах, минутах и секундах будет: 171524.
И
2ndF
ли набрать угол в градусах и десятичных долях градуса (17,25666…), а затем нажать кнопки . Высветится 17,1524; Т.е. 171524.
Перевод с градусной меры в деления угломера на микрокалькуляторе.
Пример 7. Преобразовать дирекционный угол с градусной меры = 5413 в деления угломера и обратно.
Р е ш е н и е : Градусы дел. угломера = (13 60 + 54) 6 = 9,036…= 9-03,6 е ш е н и е : Градусы дел. угломера = (13 60 + 54) 6 = 9,036…= 9-03,6
или набрать 54,13 , а затем нажать кнопку получим 54,21666…
54,21666… 6 = 9,036…= 9-03,6
Дел. угломера градусы, набрать 9,036 6 = 54,216
54,216– 54 = 0,216 60 = 12,96 13
Ответ: = 54139-03,65413
|
|
|
|
 Скачать 1.19 Mb.
Скачать 1.19 Mb.
 0-16,7;
0-16,7; 


 е ш е н и е : Градусы дел. угломера = (13 60 + 54) 6 = 9,036…= 9-03,6
е ш е н и е : Градусы дел. угломера = (13 60 + 54) 6 = 9,036…= 9-03,6

