Учебное пособие. Содержание. В 4 5 6 10 13 14 14 16 20 25 26 28 29 30 31 34 36 37
 Скачать 1.19 Mb.
|
|
Определение превышений и абсолютных высот. Высоты точек местности в России измеряются от среднего уровня Балтийского моря. C 1946 года для всей территории страны принята Балтийская система высот, по которой счет ведется от нуля Кронштадского футштока. Абсолютная высота (Н) – это расстояние по вертикали какой-либо точки на поверхности Земли до среднего уровня моря (уровенной поверхности). Относительная высота ( h ) – это высота какой-либо точки земной поверхности относительно высоты другой точки. Относительная высота – это превышение одной точки местности над другой и определяется как разность их абсолютных высот (рис.19). При подготовке данных для стрельбы артиллерии могут определяться: превышение НП (ОП) над контурной точкой – при определении высот НП (ОП); превышение цели над ОП – для определения установок для стрельбы; превышение цели над НП – при определении высоты цели. Превышение может быть определено по карте масштаба 1:25000 – 1:100000, как разность абсолютных высот точек местности (высоты определяются интерполированием относительно ближайших горизонталей). Д 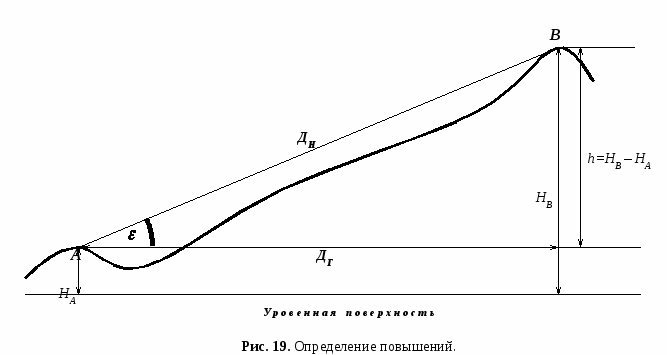 ля определения превышения на местности измеряют угол наклона (угол места цели) при наблюдении с одной точки на другую и расстояние между ними ДН (или по топографической карте ДГ).Превышение h вычисляют по формуле:  или,  (49)  (50)где,  – наклонное расстояние; – расстояние между точками, приведенное к горизонту;Вычисление превышений может выполняться аналитически, с помощью таблиц, а так же графическим построением на бумаге или ПУО с обязательным соблюдением единого масштаба дальности и превышения. Приведение наклонных расстояний к горизонту. В зависимости от вида топогеодезической привязки и требуемой точности определения координат для измерения расстояний применяют: квантовый топографический дальномер КТД-1, КТД-2; лазерным прибором разведчика (ЛПР); дальномеры ДДИ и ДДИ-3; дальномер ДСП-30; теодолит с дальномерной рейкой; буссоль с дальномерной рейкой; мерную ленту. Если измеренные расстояния имеют углы наклона, превышающие 2 при определении координат на геодезической основе или 5 при определении координат по карте, то их приводят к горизонту. Поправку Д за приведение к горизонту расстояний, измеренных квантовыми дальномерами, оптическими дальномерами по горизонтальной рейке, с помощью мерной ленты, определяют по таблице (приложение 2) « Руководства по боевой работе топогеодезических подразделений ракетных войск и артиллерии Сухопутных войск» или (приложение 9), настоящего пособия. Если расстояние измерялось оптическим дальномером по вертикальной рейке, то поправку Д, определенную по таблице, удваивают. Поправку Д всегда вычитают из измеренного расстояния. Если необходимо знать поправку Д, то ее абсолютное значение вычисляют по формуле: 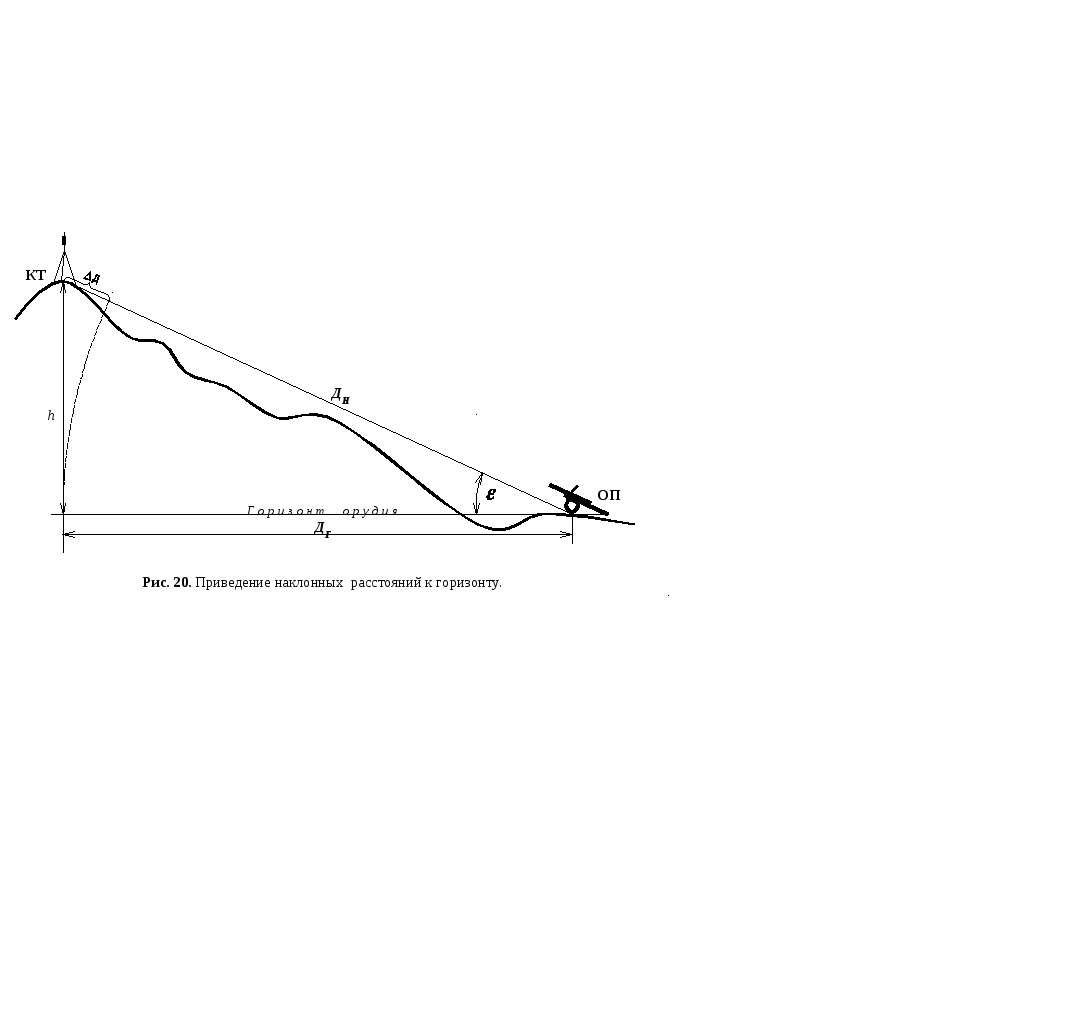 (51)   При отсутствии таблицы поправок привести линию к горизонту можно по формуле: ДГ = ДН cos (52) где ДН – дальность наклонная, измеренная на местности; – вертикальный угол (угол места цели). Определение расстояний засечкой с помощью базы. Определение расстояния засечкой с помощью базы заключается в измерении самой базы и углов на ее концах. Величину базы выбирают не менее 1/20 от определяемого расстояния и кратную 10 м. Базу, как правило, располагают под прямым углом к определяемому расстоянию.  При расположении базы Б перпендикулярно к измеряемой линии АС (рис. 21) искомое расстояние определяют с помощью таблицы (приложение 7), которая рассчитана для Б = 100 м. Входом в таблицу является угол или , если измерялся параллактический угол в точке С. Если длина базы отличается от 100 м, то дальность, определенную по таблице Дтабл., умножают на коэффициент К= Б 100, т. е. Д = Дтабл. К . Пример 1. 15-00; 13-87; Б = 90 м. Р е ш е н и е: Д = 841,1 (90 100) = 841,1 0,9 = 757 м. При отсутствии таблицы, если =15-00, расстояние достаточно просто вычислить по формуле:  (53)где, = 30-00 – ( + ); (54) В том случае, когда угол при базе не прямой, т. е. 15-00, искомое расстояние Д можно вычислить по формуле:  (55)Пример 2. =15-37; 13-45 (8042); Б = 120 м. Р е ш е н и е: + = 15-37 +13-45 = 28-82 (17255,2)  Прямая геодезическая задача. Прямая геодезическая задача (ПГЗ) на плоскости заключается в нахождении координат определенной точки по известным прямоугольным координатам заданной (исходной) точки, расстоянию между ними и дирекционному углу с заданной точки, на определяемую. На рисунке 22 показаны ОХ и ОY – координатные оси с началом координат в точке О. Через точку А и В проведем линии, параллельные осям координат, которые с линией АВ образуют прямоугольный треугольник АВС. К 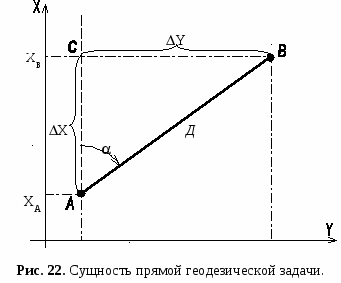 атеты прямоугольного треугольника являются проекциями прямой АВ на оси координат, которые обозначим, соответственно и , и называются приращениями координат. (ХА,YA) – известные координаты точки А. (ХВ,YB) – определяемые координаты точки В. – дирекционный угол с точки А на точку В. Д – расстояние (дальность). Прямая геодезическая задача может решаться графическим или аналитическим методом. Выбор метода и средств, для решения прямой геодезической задачи зависит от вида топогеодезической привязки и требуемой точности определения координат. Решение прямой геодезической задачи графическим методом может быть выполнено на карте (аэроснимке), планшете или на приборе управления огнем. При аналитическом решении прямой геодезической задачи приращения координат и можно определить с помощью таблиц натуральных значений тригонометрических функций, по таблицам приращений координат, на артиллерийской логарифмической линейке ЛА-14, на счислителе топографическом малом (СТМ), с помощью номограммы инструментального хода (НИХ), с помощью микрокалькулятора (ЭКВМ, ЭВМ, в т.ч. специализированных); ПГЗ решают в следующей последовательности:
 (56)
 (57)Формулы (52) и (53) являются математическим выражением прямой геодезической задачи. Прямая геодезическая задача на плоскости может быть решена вышеперечисленными способами (за исключением с помощью микрокалькулятора, ЭВМ, ЭКВМ) в том случае, когда дирекционный угол расположен в пределах первой четверти (рис. 23) , т. е. имеет значение от 0 до 90. В зависимости от расположения определяемой точки относительно заданной, направление между ними может находиться в различных четвертях окружности. Для того, чтобы в процессе вычисления приращений координат было удобно пользоваться таблицами натуральных значений тригонометрических функций, которые, как правило, составлены для острых углов первой четверти, а также на логарифмической линейке или СТМ, необходимо от исходного (заданного) дирекционного угла перейти к значению острого угла в первой четверти (рис. 23).  Знаки приращений координат ΔХ и ΔY зависят от взаимного расположения точек А и В, а следовательно, и от знаков функций синуса и косинуса дирекционного угла направления, по которому вычисляется приращение координат. На рисунке 23 также показана зависимость знаков приращений координат ΔХ и ΔY от расположения определяемой точки в четвертях окружности. Самым распространенным способом решения прямой геодезической задачи в последнее время является с помощью микрокалькулятора. Пример 1. Пусть известны прямоугольные координаты контурной точки А, дирекционный угол (в градусах) с точки А на точку В, и расстояние Д между точками А и В: XА= 67 880; YА= 18 550; = 7439; Д =1420 м. Р е ш е н и е:
= 1420 sin 74,65= +1369 м
YВ = 18 550+1369 =19 919; О т в е т: XВ = 68 256; YВ = 19 919; Пример 2. Пусть известны прямоугольные координаты контурной точки А, дирекционный угол (в дел. угломера) с точки А на точку В, и расстояние Д между точками А и В: XА= 67 630; YА= 18 290; = 26-71; Д =754 м. Р е ш е н и е:
= 754 sin 160,26 = +255 м
YВ = 18 290 + 255 = 18 545; О т в е т: XВ = 66 920; YВ = 18 545;
Обратная геодезическая задача. Обратная геодезическая задача (ОГЗ) на плоскости заключается в нахождении дирекционного угла α направления с одной точки на другую и расстояния Д между ними по прямоугольным координатам данных точек. И  з рисунка 24 и формулировки обратной геодезической задачи известны:XА,YА; XВ,YВ – прямоугольные координаты точек А и В. Требуется определить: α – дирекционный угол направления с точки А на точку В; Д – расстояние (дальность) между точками А и В. В прямоугольном треугольнике АСВ катеты АС и СВ соответствуют приращениям координат: АС = ΔХ ; СВ = ΔY; Таким образом, в прямоугольном треугольнике АСВ известны два катета, по которым можно определить все его остальные элементы: острый угол САВ, равный дирекционному углу α, и гипотенузу Д (дальность). Обратная геодезическая задача решается теми же способами и средствами, что и прямая геодезическая задача. ОГЗ решают в следующей последовательности: Пусть в точке А находится огневая позиция (ОП), а в точке В – цель (Ц). 1. По известным координатам ОП и цели вычисляют приращения координат ΔХ и ΔY:  (58)2. Определить острый угол α´ (рис. 22) по формуле:  (59)
 (60)Пример 1. По прямоугольным координатам огневой позиции XОП = 79 790, YОП = 16 350 и цели XЦ = 82 145, YЦ = 17 610 вычислить дирекционный угол α с ОП на Ц и расстояние между ними Д. Р е ш е н и е:
= 17 610 –16 350 = +1260;
 4-69;
дирекционный угол будет = 4-69;
О т в е т: = 4-69; Д = 2671 м.
|
