Учебное пособие. Содержание. В 4 5 6 10 13 14 14 16 20 25 26 28 29 30 31 34 36 37

• Название: Учебное пособие. Содержание. В 4 5 6 10 13 14 14 16 20 25 26 28 29 30 31 34 36 37
• Анкор: Uch_posobie_OEV.doc
• Дата: 05.10.2017
• Размер: 1.19 Mb.
• Имя файла: Uch_posobie_OEV.doc
• Тип: Учебное пособие; #9215
• страница: 3 из 11

Таким образом, из формулы (19) видно, что абсолютная величина сближения меридианов изменяется в зависимости от широты В и от удаленности точки от осевого меридиана. Для точек, находящихся на экваторе В=0, sin В = 0, - сближение меридианов  = 0, на осевом меридиане (L - L₀) = 0, следовательно  = 0.

Значение сближения меридианов, полученное по приведенной формуле (19), может иметь погрешность до 5. Однако, столь незначительная ошибка для топографических работ, а также для обозначения величины  на карте, значения не имеет.

Переход от магнитного азимута к дирекционному углу и обратно.

Определение поправки буссоли по данным карты.
Зависимость между магнитным азимутом и дирекционным углом, в общем виде, может быть показана на рисунке: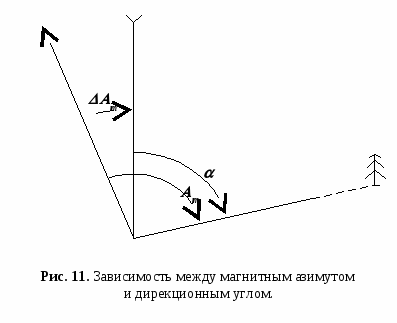




_т




_т



Для перехода от магнитного азимута к дирекционному углу легко найти выражение:

 =  _m  (_m) (22)

Формула находит практическое применение при определении дирекционного угла с помощью магнитной стрелки буссоли. Этот способ ориентирования дает возможность из непосредственных наблюдений получить магнитный азимут ориентирного направления, а зная поправку буссоли, можно вычислить дирекционный угол того же направления.

Формула перехода от дирекционного угла к поправке буссоли применяется при определении _m на местности по известному дирекционному углу на ориентир.

_m =  _m   (23)

П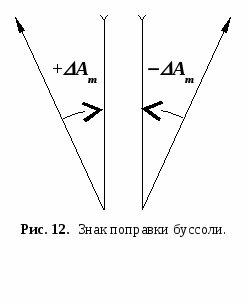оправка буссоли (А_m) – это горизонтальный угол между северным направлением магнитного меридиана (магнитной стрелки) и вертикальной линией километровой сетки.

Поправка буссоли может быть положительна «+» и отрицательна «–», (рис. 12).

«+» – если вертикальная линия координатной сетки находится восточнее магнитного меридиана.

«–» – если вертикальная линия координатной сетки находится западнее магнитного меридиана.

Составными элементами поправки буссоли являются сближение меридианов , магнитное склонение , инструментальная ошибка :

А_m=  –  +  (24)

Магнитное склонение – это горизонтальный угол между северным направлением истинного меридиана и магнитным меридианом в данной точке. Обозначается буквой  (дельта).

Инструментальная ошибка является результатом непараллельности визирной оси монокуляра и линии, соединяющей индексы ориентир-буссоли при нулевых отсчетах на буссольном кольце и барабане.

В случае, когда инструментальная ошибка прибора будет равна нулю, то поправка буссоли будет равна алгебраической разности:

А_m=  –  (25)
Определение поправки буссоли А_m по данным карты.

1. 
   Выписать склонение магнитной стрелки на год издания карты _к; Склонение выписывается в делениях угломера (западное «–», восточное «+»).
   
2. 
   Вычислить склонение магнитной стрелки на текущий год ₂₀₀₄. Для этого годовое изменение магнитного склонения , указанное на карте, необходимо умножить на количество лет п, прошедших с момента издания карты, и полученную величину алгебраически суммировать со значением склонения магнитной стрелки, указанным на карте:
   

₂₀₀₄ = _к+  n , (26)

формула верна, если годовое изменение склонения  берется в делениях угломера;

где, ₂₀₀₄ – склонение магнитной стрелки на текущий год;

_к – склонение магнитной стрелки на год издания карты;

 – годовое изменение магнитного склонения;

n – количество лет, прошедших с момента издания карты;
Для уменьшения ошибки округления, особенно при большом промежутке времени с момента издания карты, годовое изменение склонения , рекомендуется брать с карты в угловых минутах. Тогда склонение на текущий год будет:

₂₀₀₄ =_к +(  n)  3,6 (27)

3. 
   Выписать сближение меридианов  с карты в делениях угломера (восточное «+», западное «–»).
   
4. 
   Вычислить поправку буссоли на текущий год
   

А_m=  – ₂₀₀₄ (28)

Пример. Определить поправку буссоли по данным карты У-34-37-В (СНОВ).

1. 
   Склонение с карты на 1986 год: _к = +1-04
   
2. 
   Склонение на текущий год будет: ₂₀₀₄ = _к +(  n)  3,6  =
   

= +1-04 +(+002 18)  3,6 = +1-04 + 36   3,6 = +1-04 + 0-10 = +1-14

3. 
   Сближение меридианов  = – 0-39
   
4. 
   А_m=  – ₂₀₀₄ = – 0-39 – 1-14 = – 1-53
   

Для облегчения вычислений поправки буссоли на топографической карте рядом с данными о склонении магнитной стрелки и сближении меридианов под южной стороной рамки каждого листа крупного масштаба помещена схема взаимного расположения истинного, магнитного меридианов и вертикальной линии сетки. На схеме показаны и углы, связывающие эти направления, т.е.:

• 
  магнитное склонение _к ( в градусной мере);
  
• 
  среднее сближение меридианов  ( в градусной мере);
  
• 
  поправка буссоли А_m на год издания карты с учетом знака (в делениях угломера).
  

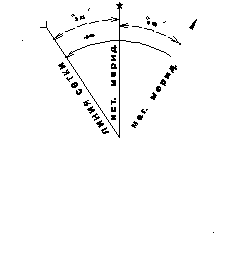Склонение на 1986 г. восточное 615 (1-04). Среднее сближение меридианов западное 221 (0-39). При прикладывании (компаса) к вертикальным линиям координатной сетки среднее отклонение магнитной стрелки восточное 836 (1-43). Годовое изменение склонения восточное 002 (0-01). Поправка в дирекционный угол при переходе к магнитному азимуту минус (1-43).

Примечание. В скобках показаны деления угломера (одно деление угломера = 3,6).

Рис. 13. Данные о склонении магнитной стрелки и

сближении меридианов, помещаемых на картах.
На листе карты У-34-37-В (СНОВ), на схеме поправка буссоли на год издания карты (на 1986 г.) составляла А_m = – 1-43

Для получения поправки буссоли на текущий год, необходимо учесть только годовое изменение склонения, а именно, в какую сторону и на сколько делений угломера переместилась магнитная стрелка за прошедшие годы.

Если годовое изменение склонения восточное, то магнитная стрелка смещалась на восток, если годовое изменение склонения западное, то – на запад.
Величину смещения в делениях угломера вычислим, умножив годовое изменение склонения в минутах на количество лет, и разделим на 3,6.

(  n)  3,6  = (2 18)  3,6 = 0-10

И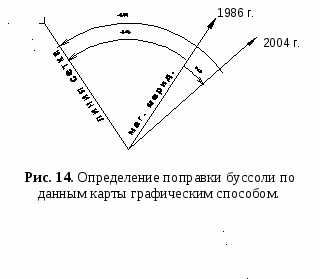з рисунка 14 видно, что поправка буссоли в 2004 году, по модулю, увеличится на 0-10, сохранив знак «–», т. е. составит –1-53.
Таким образом, поправку буссоли легче получить графическим методом, по схеме, задаваемой на карте, а при отсутствии схемы по формулам.

Изменение поправки буссоли при перемещении на местности

в новый район.
Известно, что величину поправки буссоли А_m составляют сближение меридианов , магнитное склонение  и инструментальная ошибка .

А_m=  –  +  (24*)

Инструментальная ошибка  является постоянной (систематической) ошибкой данного прибора и может достигать значительной величины. Наличие инструментальной ошибки вызывает необходимость определить поправку буссоли каждого прибора и исключает возможность пользоваться поправкой буссоли, определенной для данной местности другим прибором. Но так как эта ошибка является постоянной (систематической), то, зная значение изменения поправки буссоли в новом районе, можно вычислить новое значение поправки буссоли для данного прибора по результатам измерений, выполненных с помощью одной из буссолей подразделения (части).

Величина сближения меридианов не меняется во времени, но изменяется при перемещении в новый район.

Изменение величины сближения меридианов при перемещении в новый район можно определить, а значит, и уточнить поправку буссоли.

Е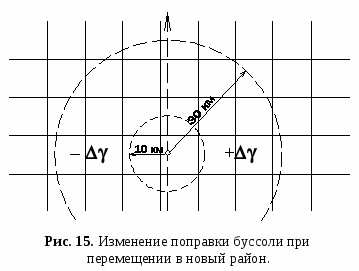сли в новом районе нет возможности сразу же определить поправку буссоли А_m, разрешается пользоваться поправкой для старого района (при перемещении на расстояние до 30 км в пределах одной зоны), вводя в не поправку на изменение сближения меридианов :

А_{m нов.}= А_{m ст.}   (29)

Если новый район расположен восточнее старого, поправку  берут со знаком «плюс», если западнее – «минус».
В неаномальных районах в радиусе 10 км от точки определения поправка буссоли принимается неизменной (рис. 15).

Поправку  берут из таблицы, приложение 4 «Руководства по боевой работе топогеодезических подразделений…», или по графику приложение 4 настоящего пособия, по абсциссе Х в км района развертывания и по дальности перемещения Д по Y.

Дальность Д (в километрах) определяется по карте как разность координаты Y:

Y = Y_нов. – Y_ст. (30)

где, Y_ст. – координата старого места выверки

Y_нов. – координата нового района.

Пример.

Батарея в ходе боевых действий переместилась

из старого района (Х_ст= 6 050 200; Y_ст.=3 422 800)

в новый район (Х_нов.= 6 070 300; Y_нов.=3 400 800).

Уточнить поправку буссоли в новом районе, если А_{m ст.} = +0-62.

Р е ш е н и е:

1). Определим расстояние в километрах, на которое переместилась батарея

Y = Y_нов. – Y_ст. = 400 – 423 = –23 км

Знак «–» указывает, что батарея переместилась на запад от старого района.

Так как батарея переместилась на 23 км западнее, то поправку буссоли уточняем по формуле (20):

А_{m нов.}= А_{m ст.}  

где – А_{m нов} – поправка буссоли в новом районе;

 – величина изменения сближения меридианов.
2). Из таблицы (приложение 4, «РБР ТГП РВ и А СВ») или по графику выбираем  по аргументам Х_нов. = 6070 км и Y = 23 км

 = 0-04

Тогда, А_{m нов.}= А_{m ст.}   = +0-62 – 0-04 = +0-58

Ответ: А_{m нов.}= +0-58

Тригонометрические функции острого угла.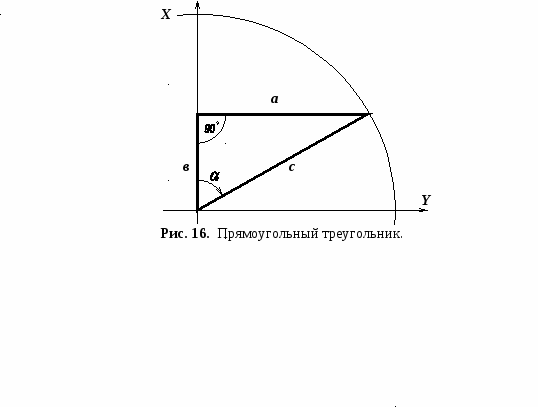



Тригонометрическими функциями острого угла называются числовые значения взаимного отношения любых двух сторон прямоугольного треугольника. В зависимости от того, отношения каких сторон прямоугольного треугольника рассматриваются, тригонометрические функции носят названия: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg) и др.
Синусом острого угла называется числовое значение отношения длины противолежащего катета к длине гипотенузы:

(31)

Косинусом острого угла называется числовое значение отношения длины прилежащего катета к длине гипотенузы:

(32)

Тангенсом острого угла называется числовое значение отношения длины противолежащего катета к длине прилежащего катета:

(33)

Котангенсом острого угла называется числовое значение отношения длины прилежащего катета к длине противолежащего катета:

(34)

Функции острых углов играют важную роль при решении многих математических и топогеодезических задач, однако их использование ограничено пределами изменений острых углов от 0(0-00) до 90 (30-00). При топогеодезической привязке в системе определения дирекционных углов используются углы (направления) с пределами измерений до 360 (60-00). Поэтому возникает необходимость распространения понятия тригонометрических функций на углы любой величины.

Тригонометрические функции любого произвольного угла можно выразить через значения тригонометрических функций острого угла (угла I четверти, смотри рисунок 23). Учитывая такие преобразования, составлена "Таблица натуральных значений тригонометрических функций синусов и косинусов" (Приложение 6). По таблице можно определить тригонометрические функции синуса и косинуса, не приводя угол к I четверти.
Решение треугольника.
С решением треугольника связаны все виды засечек. Решить треугольник, – это значит, определить неизвестные значения угловых и линейных элементов. Для решения треугольника необходимо знать значения трех любых его элементов, из них должна быть хотя бы одна сторона.

В практике топогеодезических работ привязка элементов боевого порядка засечками сводится к вычислению по известным двум углам и одной стороне третьего угла и двух других сторон или к вычислению по известным двум сторонам и углу между ними третьей стороны и двух углов.

Решение треугольника осуществляют по формулам соотношений его элементов, известных из курса тригонометрии.

Обозначив в треугольнике АВС (рис. 17) стороны через , и а углы через А, В и С, запишем основные соотношения:
(теорема суммы углов); (35)
(теорема синусов); (36)
(теорема косинусов); (37)
(теорема тангенсов). (38)
Рассмотрим применение данных теорем при решении треугольника.
Решение треугольника по двум углам и одной стороне.



Последовательность решения:

1. 
   Находят угол С из теоремы суммы углов по формуле
   

или ; (39)

2. 
   Длины сторон и вычисляют по теореме синусов по формулам
   

3. 
   Контроль вычислений осуществляют по формуле
   

(42)
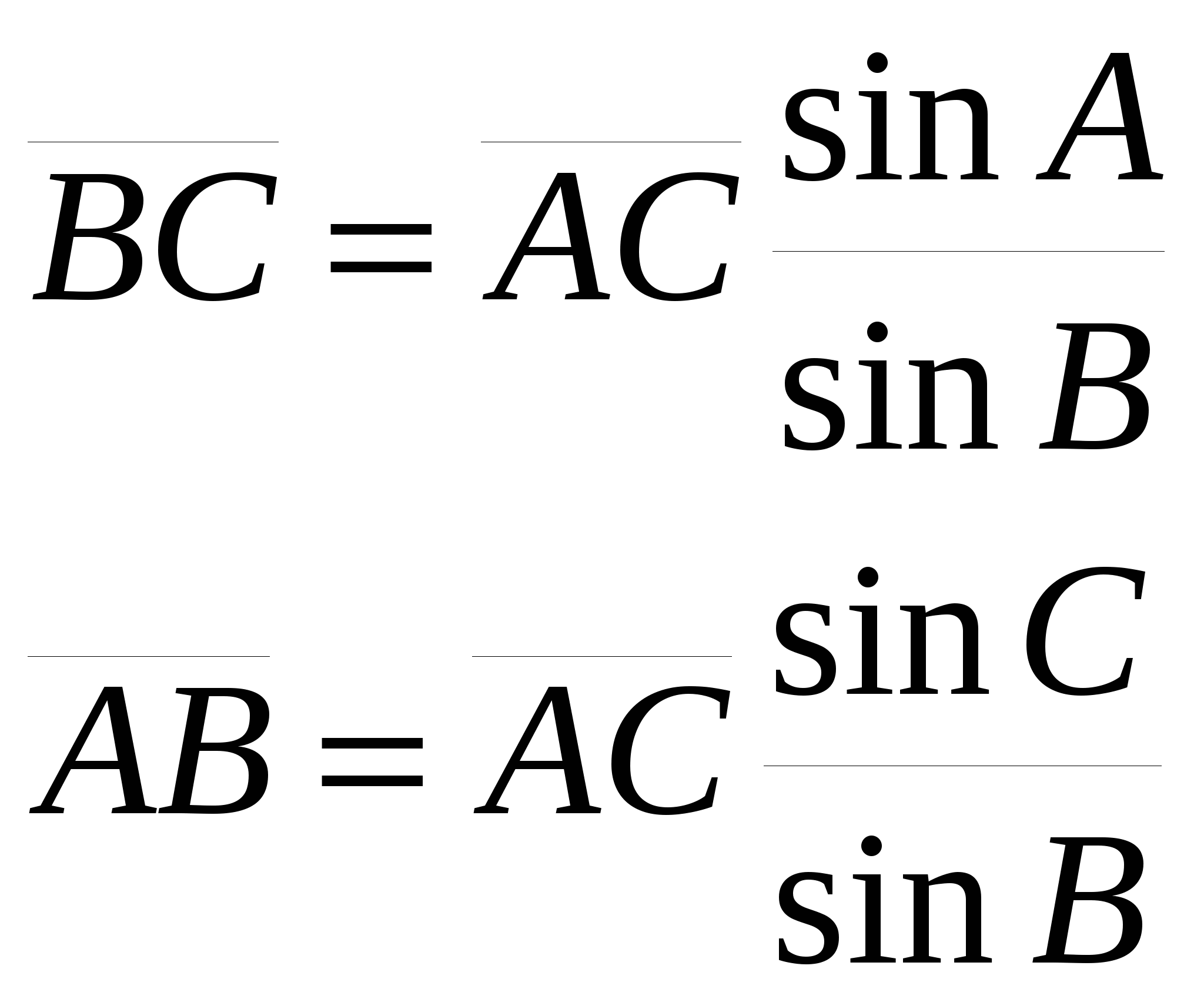
Решение треугольника по двум сторонам и углу между ними.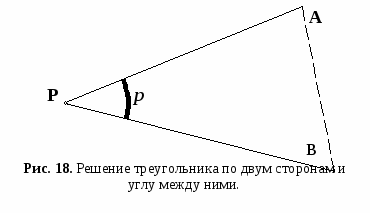


Последовательность решения:

1. 
   Определить полусумму углов А и В по формуле:
   

(43)

2. 
   Определить величину по формуле:
   

(44)

3. Определить полуразность углов А и В по формуле:

(45)

4. Вычислить углы А и В по формулам:

и (46)

5. Вычислить длину стороны 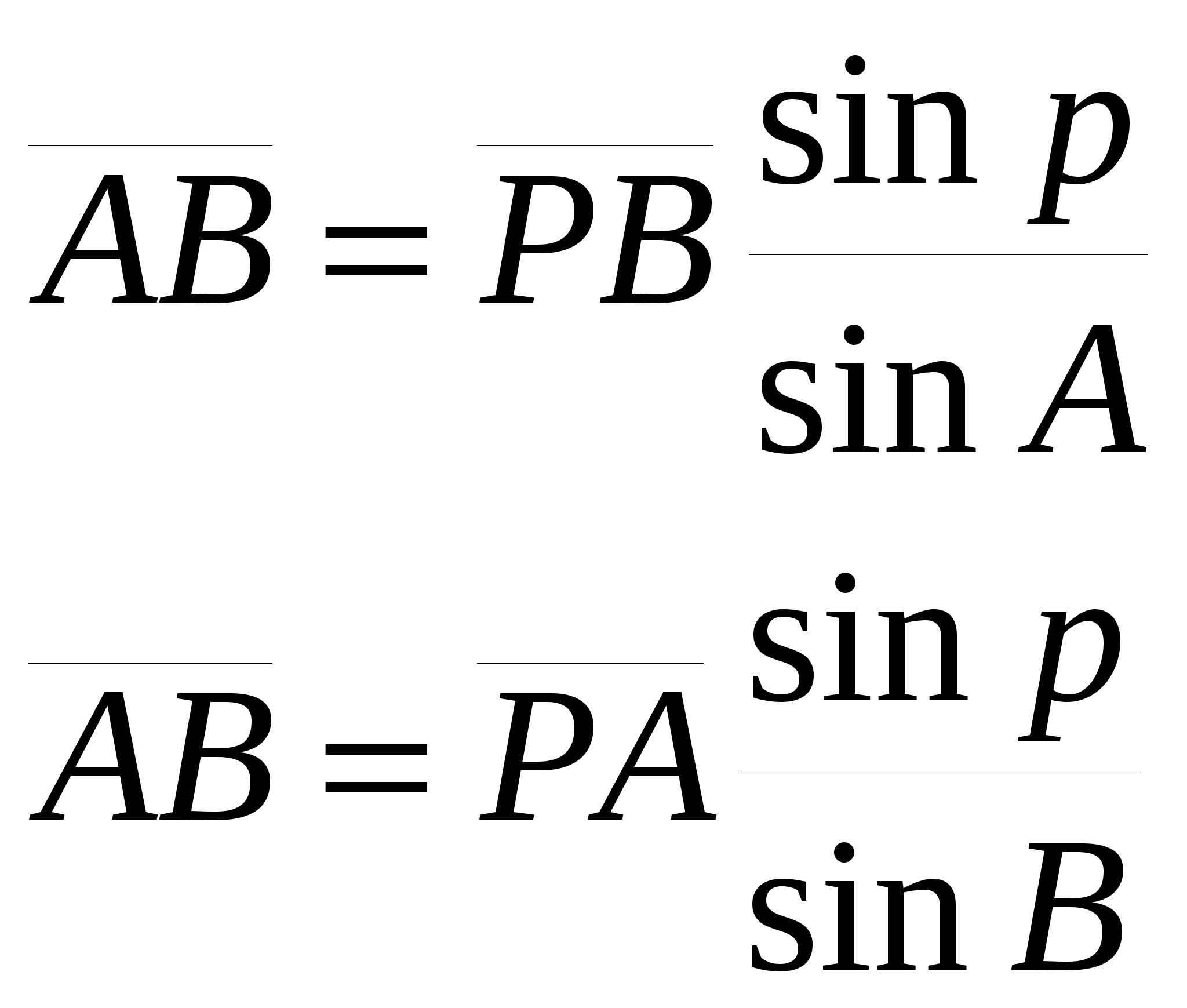по формулам: