Учебное пособие. Содержание. В 4 5 6 10 13 14 14 16 20 25 26 28 29 30 31 34 36 37
 Скачать 1.19 Mb.
|
|
Зависимость между линейной и угловой величинами. Решая задачи с помощью "тысячной" необходимо сделать два допущения: дуга, соответствующая углу в одно деление угломера, принимается равной хорде; одно деление угломера принимается равным  вместо  ; Делая точные расчеты, необходимо учитывать эти допущения, т. е. вводить соответствующую поправку. Расчеты показывают, что разность между величиной дуги и величиной хорды незначительна: при углах до 3-00 разность меньше 0-01; при углах от 3-00 до 5-00 разность от 0-01 до 0-06. Относительную величину ошибки, которая будет иметь место из-за того, что одно деление угломера принято равным вместо , вычислим:  т. е. 5%.Это значит, что при решении задач, рассчитанную по "тысячной" величину угла следует исправлять на 5% (или на 1/20). "Тысячная", принятая за меру углов в артиллерии, позволяет решать практические задачи в уме очень быстро и довольно точно. Чтобы научиться решать эти задачи, установим зависимость между угловыми и линейными величинами, а именно: линейное расстояние между двумя равноудаленными от наблюдателя точками равно угловому расстоянию между ними в делениях угломера, умноженному на 0,001 дальности. Обозначим расстояние между двумя равноудаленными от центра точками А и В через  , угол между направлениями на них через и расстояние от наблюдателя до точек Д (рис. 2).Известно, что длина дуги равна одной тысячной R:  или для принятых обозначений  Так как угол между равноудаленными точками А и В в раз больше тысячной, то длина дуги АВ будет больше  в раз:  или  При углах до 3-00 допускается, что длина дуги примерно равна длине соответствующей хорды, т. е.   Следовательно,  или в другом виде: (8)Принимая за неизвестное ту или другую величину, входящую в формулу, можно решить три типа задач: зная угол между двумя равноудаленными точками и дальность до них Д, определяют расстояние между ними по формуле:; (8*)зная расстояние между двумя точками и дальность до них Д, определяют величину угла в делениях угломера , между направлениями на эти точки по формуле: ; (9)зная расстояние между двумя точками и величину угла между направлениями на них , определяют дальность Д по формуле: ; (10)Эти формулы дают результат не точный, т.к. в них не учтена 5% поправка. Для более точных расчетов в формулах вместо 1000 необходимо брать 955. При определении Д и , 1000 стоит в числителе, следовательно, конечный результат будет больше точного. Поэтому в формулах (9) и (10) результат необходимо уменьшить, а в формуле (8) результат необходимо увеличить на 5% . Пример 8. Угловое расстояние между двумя равноудаленными от наблюдателя предметами равно = 0-25. Определить расстояние l между этими предметами, если дальность Д до них равна 5000 м. Р е ш е н и е : Линейное расстояние между этими предметами будет равно  Если требуется получить более точные расчеты, необходимо в полученный результат внести поправку на ошибку округления, т.е. увеличить на 5%:  Окончательный результат: l = 125 + 6 = 131 м. Пример 9. Определить расстояние до рейки высотой 3 м при условии, что рейка видна под углом в 0-15. Р е ш е н и е :  или, более точно, с поправкой на округление:  Пример 10. Расстояние (дальность) от батареи до цели 4800 м. Фронт цели в метрах равен 260 м. Определить фронт цели ФЦ в делениях угломера. Р е ш е н и е : Из рис. 1, фронт цели в делениях угломера ФЦ=.  (0-54) или, более точно (0-51)О т в е т. Фронт цели равен ФЦ = 0-51. Азимуты и дирекционный угол. При ориентировании на местности по карте или аэрофотоснимку, по приборам наземной навигации, при движении по азимуту, нанесении на карту или схему разведанных объектов и целей, при определении дирекционных углов ориентирных направлений, подготовке данных для стрельбы артиллерии, и в других случаях, часто возникает необходимость в определении направлений на какие-либо точки местности относительно направления, принятого за начальное. В качестве начального направления обычно принимают направление, параллельное вертикальной линии координатной (километровой) сетки, направление истинного (геодезического, географического) меридиана, направление магнитного меридиана (направление магнитной стрелки). В зависимости от начального направления, различают три вида углов, определяющих направления на точки: дирекционный угол, истинный (геодезической, географический) азимут, магнитный азимут (рис. 3). Чтобы не допускать ошибок при вычислениях, необходимо помнить основные определения:    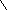  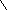 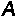Дирекционный угол () – это горизонтальный угол, отсчитываемый по ходу часовой стрелки от северного направления вертикальной линии координатной сетки карты до направления на ориентир. Отсчитывается от 0(0-00) до 360(60-00). Истинный азимут (А) – это горизонтальный угол, отсчитываемый по ходу часовой стрелки от северного направления истинного меридиана до направления на ориентир. Отсчитывается от 0(0-00) до 360(60-00). Магнитный азимут (т) – это горизонтальный угол, отсчитываемый по ходу часовой стрелкиот северного направления магнитного меридиана (магнитной стрелки) до направления на ориентир. Отсчитывается от 0(0-00) до 360(60-00). Прямой и обратный дирекционный угол. Дирекционный угол какого-либо направления с точки А на точку В (рис. 4) принято обозначать (АВ) или АВ(в разных источниках можно встретить различные обозначения). Первая пишется буква, обозначающая ту точку, от которой идет направление.  Таким образом, дирекционный угол направления с точки В на точку А обозначают (ВА), будет обратным. Если направление с точки А на точку В считается п р я м ы м, то направление с точки В на точку А будет о б р а т н ы м, и наоборот. Значения прямого (АВ) и обратного (ВА) дирекционных углов одного и того же направления отличаются на 180 (30-00). (ВА) = (АВ) 180 ; (ВА) = (АВ) 30-00 (11) Таким образом, обратный дирекционный угол равен прямому, измененному на 180 (на 30-00). Пример. (к рис.3). прямой (АВ)= 5713 , обратный (ВА)= 23713 (АВ)= 10-39 , (ВА)= 40-39 Определение величины горизонтального угла по дирекционным углам направлений, составляющих этот угол, и наоборот. Величину горизонтального угла по дирекционным углам направлений, составляющих этот угол, и переход от дирекционного угла одного направления к дирекционному углу другого направления исходящим из одной и той же точки приходится выполнять при вычислениях теодолитных (буссольных) ходов, прямых и обратных засечек, определении дирекционного угла продольной оси топопривязчика (машины), а также при выполнении графических построений и измерений на карте (планшете). И  звестно, что дирекционные углы возрастают по ходу часовой стрелки, так же, как и подписи делений лимба угломерных приборов. Поэтому у любого горизонтального угла MAN (угол между левым и правым направлением) дирекционный угол правой стороны (АN) больше дирекционного угла левой стороны (АM). Отсюда правило: величина горизонтального угла равна разности: дирекционный угол правого направления минус дирекционный угол левого направления (рис. 5). (АN) (АМ) (12) И как следствие данного правила, следующие правила: дирекционный угол правого направления (АN) горизонтального угла равен дирекционному углу левого направления (АМ) плюс горизонтальный угол между ними . (АN) = (АМ) + (13) дирекционный угол левого направления (АМ) горизонтального угла равен дирекционному углу правого направления (АN) минус горизонтальный угол между ними . (АМ) = (АN) (14) Пример 1. (к рис. 5) 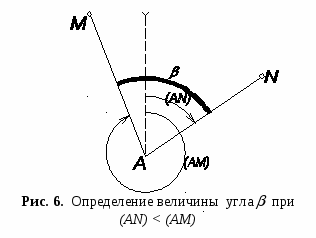 = 12537 5713 = 6824(АN) = 5713 + 6824 = 12537 (АМ) = 12537 6824 = 5713 Если в (12) и (14) вычитаемое больше уменьшаемого, то ко второму необходимо прибавить 360 (60-00). Если в результате сложения двух углов в (13), получена в сумме величина, превышает 360 (60-00), то эта сумма уменьшается на 360 (60-00). Пример 2. (к рис.6) = 7443 34522 = 43443 34522 = 8921 (АN) = 34522 + 8921 = 43443 = 7443 (АМ) = 7443 8921 = 43443 8921 = 34522 Переход от истинного азимута к дирекционному углу. Определение сближения меридианов. П 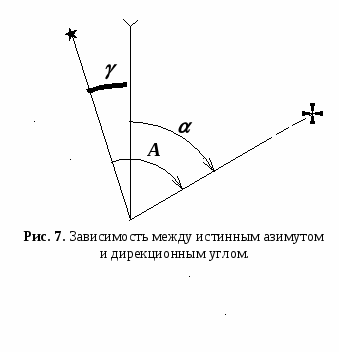 ри выполнении топогеодезических работ необходимо определять дирекционные углы ориентирных направлений, которые непосредственно получить не всегда возможно. Из астрономических наблюдений или с помощью гирокомпаса определяют истинные азимуты ориентирных направлений, а затем переходят к дирекционным углам этих направлений, учитывая сближение меридианов, по формуле: (15)Т   .е. дирекционный угол любого направления есть разность между истинным азимутом этого направления и сближением меридианов в данной точке (со своим знаком).Переход от дирекционного угла ориентирного направления к его истинному азимуту осуществляют по формуле:  (16)Переход от дирекционного угла ориентирного направления к его истинному азимуту необходим при определении истинного азимута эталонного направления, при определении поправки гирокомпаса.  И в том и в другом случае возникает необходимость в определении сближения меридианов. Сближение меридианов – это горизонтальный угол между северным направлением истинного меридиана данной точки и северным направлением вертикальной линии координатной сетки карты. Сближение меридианов обозначается греческой буквой (гамма). На топографической карте направлению истинного меридиана соответствуют боковые стороны рамки листа карты, а направлению, параллельному осевому меридиану (оси абсцисс) – вертикальные линии координатной (километровой) сетки. Линии координатной сетки карты не совпадают с направлениями истинных меридианов, потому что истинные меридианы представляют собой дуги, которые сходятся у полюсов в одной точке, а вертикальные линии сетки в пределах одной зоны остаются параллельными друг другу. Отсчет сближения меридианов ведется от истинного меридиана. Поэтому, = 0, если точка лежит на осевом меридиане зоны, и на экваторе, т.к. истинные меридианы пересекаются с экватором под прямым углом (В = 0о). Для всех остальных точек в пределах одной шестиградусной зоны сближения меридианов по абсолютной величине не превышает = 3, (max у полюсов). Д  ля всех точек, расположенных в восточной половине координатной зоны (относительно осевого меридиана зоны), сближение меридианов имеет положительное значение и называется в о с т о ч н ы м, а для точек расположенных в западной половине зоны, оно имеет отрицательное значение и называется з а п а д н ы м.Сближение меридианов может быть определено: по карте; по графику; по формуле. При определении сближения меридианов по карте пользуются формулой: = к+ (17) где, к – сближение меридианов для центра листа карты, подписанное под южной рамкой листа карты; – поправка на смещение точки относительно центра листа карты по долготе ( по ординате Y в км). Выбирается по таблице приложения 4, «Руководства по боевой работе топогеодезических подразделений РВ и А СВ», 1985 г. стр. 135, или по графику определения поправки (Приложение 4). Поправку выбирают из таблицы, по абсциссе Х точки в километрах, и удалению точки от центра карты в километрах по Y. Если точка расположена восточнее центра листа карты, то учитывают со знаком «+», если западнее – то «–», т.е.: = к +() (18) Пример. Определить сближение меридианов по карте У-34-37-В (СНОВ) для НП, расположенного на высоте 167,7 (7207) – геодезический пункт. Р е ш е н и е: среднее сближение меридианов, указанное на карте, к = –0-39. Значение координаты Х в километрах Хкм = 6072 км. НП расположено западне центра листа карты, на удалении 8 км. Следовательно, = –0-02. Вычисляем сближение меридианов: = к + = –0-39 +(–0-02) = –0-41 Для определения сближения меридианов по графику необходимо знать полные прямоугольные координаты точки (Х, Y). С помощью графика сближение меридианов определяется с точностью 1 (0-01). Кроме графиков для определения сближения меридианов могут составляться таблицы. График для определения сближения меридианов дается в приложении 3, «Руководства по боевой работе топогеодезических подразделений …», 1985 г., стр. 134, или приложение 4, настоящего пособия. Для практического использования и более точного определения сближения меридианов график вычерчивают в подразделении на миллиметровой бумаге с увеличением в 2-3 раза. Пример. Определить сближение меридианов для района КНП 4 батареи высота с отметкой 237.3 (7015), карта У-34-37-В (СНОВ). 1. Определяем полные координаты КНП: Х = 6 070 080 Y = 4 315 170 2. Округляем Х и Y (отбрасываем метры и номер зоны): Х = 6 070 км Y = 315 км 3. Определяем сближение меридианов по графику: = –223 (–0-40) Для определения сближения меридианов по формуле используются геодезические координаты B, L.  = (L-L0)sinB (19)где, L - долгота заданной точки; L0 - долгота осевого меридиана зоны, в которой находится заданная точка; B - широта заданной точки. Знак сближения меридианов зависит от знака разности долготы (L – L0). Геодезические координаты В и L, необходимые для вычисления сближения меридианов, определяются по топографической карте с точностью до 0,5. Долгота осевого меридиана зоны определяется по формуле: L0 = 6oN-3o (20) где, N - номер координатной зоны, в которой находится заданная точка. Номер координатной зоны определяется по полной ординате Y (по карте) или по формуле:  (21)причем,  - берется только целая часть (дробная отбрасывается).Пример. Вычислить сближение меридианов для точки с геодезическими координатами: В = 5646,2; L = 6040,1; Р е ш е н и е: 1. Определяем номер зоны: N= L6о+1= 6040,1 6о = 10+1=11; 2. Вычисляем долготу осевого меридиана зоны: L0 = 6N –3 = 611 – 3 = 66 – 3 = 63 3. Вычисляем разность долгот: (L – L0) = (6040,1 – 63) = –219,9 = –139, 9 4. Вычисляем сближение меридианов: = (L – L0) sinB = = –139, 9sin 5646,2 = –139, 9 0,836 = –117 = –157 (–0-32,5) Долготу осевого меридиана L0 легко вычислить, зная долготы границ 6-ти градусных зон (рис.10):  Например: Для точки М имеющей долготу L = 6040,1 (рис.10) граница зоны слева будет 60 (число, делящееся на 6 без остатка) а справа, следовательно, 66. Зная, что осевой меридиан делит зону пополам, долгота его будет равна среднему значению L0 = (60+ 66) 2 = 63 или L0 = 60+ 3 = 63 L0 = 66- 3 = 63
|