Руководство по работе с графической библиотекой OpenGL. Руководство разработано с учетом опыта чтения курса Компьютерная графика
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
|
return true ; BOOL res = wglMakeCurrent (m_dc, m_glrc); return (res != FALSE); } bool GLRC:: Create () { assert ( !m_created ); int nPixelFormat = 0; DWORD flags ; flags = Pro_DRAW_TO_WJNDOW | PFD_SUPPORT_OPENGL | PFD_DOUBLEBUFFER; static PKELFORMATDESCRIPTOR pfd = { sizeof (PLXELFORMATDESCRIPTOR) , 1, flags , PFD_TYPE_RGBA, 24, О, О, О, О, О, О, 1, о, о, о, о, о, о, 32, о, о, PFD_MAIN_PLANE, О, О, О, О }; pfd . cAlphaBits = 8; nPixelFormat = ChoosePixelFormat ( m_dc, &pfd ); BOOL res = SetPixelFormat ( m_dc, nPixelFormat, &pfd ) ; if (res = FALSE) return false ; m_glrc = wglCreateContext ( m_dc ); m_created = true ; return MakeCurrent (); } void GLRC:: SwapBuffers () { assert (m_created ) ; : : SwapBuffers (m_dc); Б. 5. Класс для работы с OPENGL в WIN32 199 } bool GLRC : : IsCurrent () const { assert ( m_created ); return :: wglGetCurrentContext () = m_glrc; } bool GLRC:: IsCreatedQ { return m_created; } Приложение В. Примеры практических заданий В.1. Cornell Box Целью задания является создание изображения заданной трехмерной статичной сцены средствами OpenGL с использованием стандартных геометрических примитивов. Требуется создать изображение сцены Cornell Box. Эта классическая сцена представляет собой комнату кубического вида, с отсутствующей передней стенкой. В комнате находятся геометрические предметы различных форм и свойств (кубы, параллелепипеды, шары), а также протяженный источник света на потолке. Присутствует также камера с заданными параметрами (обычно она расположена так, чтобы была видна вся комната). В одной из лабораторий Корнельского университета такая комната существует в реальности, и ее фотографии сравниваются с изображениями, построенными методами трассировки лучей для оценки точности методов. На странице лаборатории (http://graphics.cornell.edu) можно найти описание геометрии сцены в текстовом формате. 201  202 Приложение В. Примеры практических заданий Рис. В.1. Пример сцены Cornell Box. Реализации сцены, приведенной на рисунке В.1, достаточно для выполнения задания, хотя возможно введение новых предметов дополнительно к существующим или вместо них. Приветствуется использование примитивов библиотек GLUT и GLU. Внимание! Сцена не должна превращаться в набор разнородных предметов. Эстетичность и оригинальность выполненного задания принимается во внимание. Протяженный источник света на потолке комнаты можно эмулировать несколькими точечными источниками. За простейшую реализацию сцены ставится 7 баллов. Реалистичность сцены можно значительно повысить за счет разбиения многоугольников. Суть этого в том, что в модели освещения OpenGL освещенность вычисляется в вершинах многоугольника с учетом направления нормалей в этих вершинах, а затем линейно интерполируется по всей поверхности. Если используются относительно большие многоугольники, то, очевидно, невозможно получить действительно плавные переходы и за- B.l. CORNELL BOX 203 тенения. Для преодоления этого недостатка можно разбивать большие грани (стены, например) на множество меньших по размерам. Соответственно разброс в направлении нормалей в вершинах одного многоугольника не будет столь велик и затенение станет более плавным (1 балл). Наложение текстур на объекты сцены поощряется 2-мя баллами. Дополнительными баллами оценивается присутствие в сцене теней. Один из простейших алгоритмов наложения теней приведен в разделе 8.2. За его реализацию можно получить до 2 баллов. Использование более продвинутых алгоритмов (например, shadow volumes) будет оценено дополнительными баллами. Реализация устранения ступенчатости (antialiasing) методом, предложенным в разделе 8.1 или каким-либо другим, оценивается в 2 балла. За введение в сцену прозрачных объектов и корректный их вывод дается 1 балл. Механизм работы с прозрачными объектами описан в разделе 7.1. Задание оценивается, исходя из 15 баллов. В приведенной ниже таблице указано распределение баллов в зависимости от реализованных требований:
Дополнительные баллы можно получить за хорошую оптимизацию программы, необычные решения, эстетичность и т.д. 204 Приложение В. Примеры практических заданий В.2. Виртуальные часы Целью задания является создание трехмерной интерактивной модели аналоговых часов.  Рис. В.2. Пример трехмерных виртуальных часов. Обязательные требования к программе: Программа должна демонстрировать на экране трехмерную модель часов. Часы могут быть любые, от наручных до кремлевских. Проявите в полной мере Вашу фантазию и чувство меры! Постарайтесь сделать как можно более реалистичную сцену. Поощряется подробная детализация элементов часов. Часы на экране обязательно должны иметь минутную и часовую стрелки. Секундная — по желанию, но очень приветствуется (иначе трудно будет определить, ходят часы или нет). В.2. Виртуальные часы 205 Время на часах должно совпадать с системным временем компьютера. Часы обязательно должны ходить, т.е. стрелки должны двигаться, и скорость их движения не должна зависеть от производительности компьютера, а определяться только текущим временем. Сцена должна быть интерактивной, т.е. давать приемлемую частоту кадров в секунду (>10) при визуализации на машине с аппаратным ускорителем трехмерной графики. Если программа будет работать медленно, баллы могут быть снижены. Необходимо реализовать вращения часов (или, возможно, камеры) с помощью мыши (предпочтительно) или клавиатуры. Можно также предусмотреть режимы с автоматическим вращением. Пожелания к программе: Поощряется введение дополнительной геометрии. Например, ремешков, маятников и т.д. Можно сделать часы с кукушкой, будильник и т.п. Желательно наличие возможностей для управления процессом визуализации. Например, наличие/отсутствие текстур, режимы заливки, детализации и т.д. Приветствуется выполнение задания в виде демонстрации, т.е. с возможностью работы в полноэкранном режиме и немедленным выходом по клавише Escape. Можно написать программу как Screen Saver. Постарайтесь использовать максимум возможностей библиотеки OpenGL. Блики, отражения, спецэффекты — за все это обязательно даются дополнительные баллы. 206 Приложение В. Примеры практических заданий • Проявите вкус — сделайте так, чтобы нравилось прежде всего Вам. Но не увлекайтесь — оставайтесь реалистами. Максимальная оценка — 20 баллов. За минимальную реализацию требований ставиться 10 баллов. Еще до 10 баллов можно получить за использование в работе возможностей OpenGL (текстур, прозрачности, сферического текстурированяи и пр.), оригинальных и продвинутых алгоритмов, количество настроек, а также за эстетичность и красоту сцены. В.З. Интерактивный ландшафт Целью данного задания является генерация и вывод с помощью OpenGL поверхности ландшафта, а также обеспечение интерактивного передвижения над ней. Рис. В.З. Пример трехмерного ландшафта. 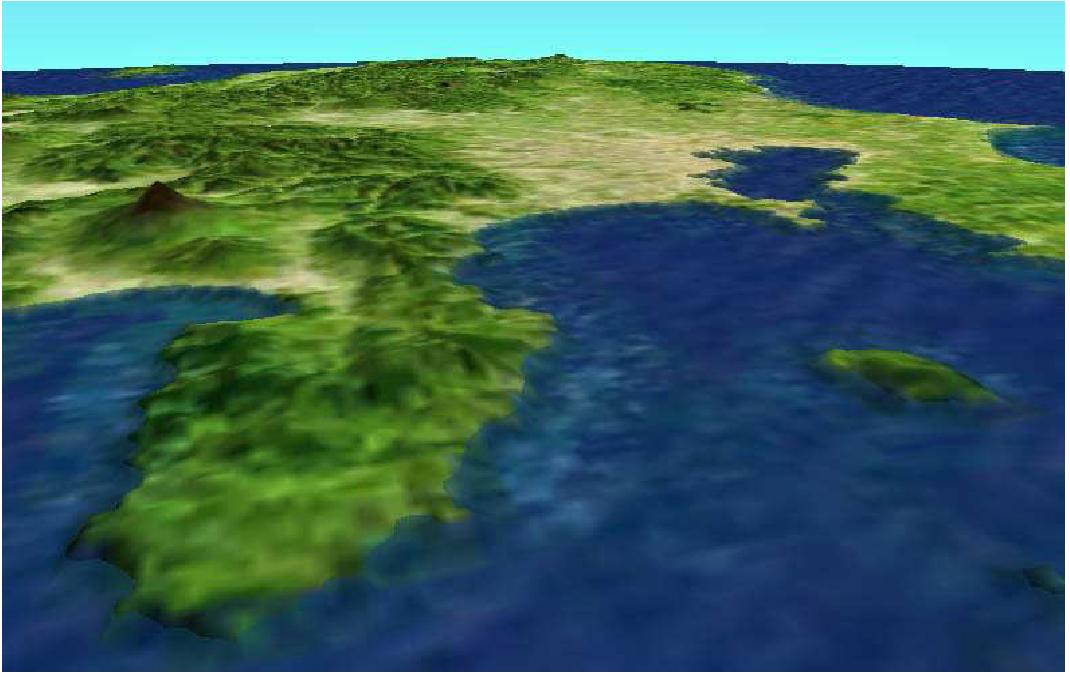 В.З. Интерактивный ландшафт 207 Обязательная часть задания Для выполнения обязательной части задания необходимы: генерация трехмерного ландшафта раскраска для придания реалистичности эффект тумана возможность «полета» над ландшафтом (управление) Более подробное описание: Генерация ландшафта Один из вариантов задания поверхности ландшафта — задание так называемого «поля высот» — функции вида z = f(x,y), которая сопоставляет каждой точке (х, у) плоскости OXY число z — высоту поверхности ландшафта в этой точке. Один из способов задания функции / — табличный, когда функция / представляется матрицей Т размера М х N, и для целых х и у / = Т[х, у], а для дробных х и у из диапазонов [0..М — 1] и [0.../V — 1] соответственно, / вычисляется интерполяцией значений / в ближайших точках плоскости OXY с целыми ж и у, а вне указанных диапазонов х и у значение функции считается неопределенным. Допустим, в памяти лежит двухмерный массив со значениями матрицы Т. Пусть N = М. Если теперь для каждого квадрата [х, х + 1] х [у, у + 1], где х ш у принадлежат диапазону [0..N — 2] построить две грани: ((х,у,Т[х,у]),(х + 1,у,Т[х + 1,у]),(х + 1,у + 1,Т[х + 1,у + 1]))и((х,у,Т[х,у]),(х + 1,у + 1,Т[х + 1,у + 1]),(х,у + 1,Т[х,у + 1])), то мы получим трехмерную модель поверхности, описываемой матрицей Т. Но каким образом задать массив значений матрицы Т? Один из способов — сгенерировать псевдослучайную поверхность с по- 208 Приложение В. Примеры практических заданий мощью фрактального разбиения. Для этого положим размерность матрицы Т равной 2 + 1, где N — натуральное число. Зададим некоторые произвольные (псевдослучайные) значения для четырех угловых элементов матрицы . Теперь для каждого из четырех ребер матрицы (это столбцы или строки элементов, соединяющие угловые элементы) вычислим значение элемента матрицы Т, соответствующего середине ребра. Для этого возьмем среднее арифметическое значений элементов матрицы в вершинах ребра и прибавим к получившемуся значению некоторое псевдослучайное число, пропорциональное длине ребра. Значение центрального элемента матрицы вычислим аналогично, только будем брать среднее арифметическое четырех значений элементов матрицы в серединах ее ребер. Теперь разобьем матрицу на четыре квадратные подматрицы. Значения их угловых элементов уже определены, и мы можем рекурсивно применить к подматрицам описанную выше процедуру. Будем спускаться рекурсивно по дереву подматриц пока все элементы не будут определены. С помощью подбора коэффициентов генерации псевдослучайной добавки можно регулировать «изрезанность» поверхности. Для реалистичности поверхности важно сделать величину псевдослучайной добавки зависящей от длины текущего ребра — с уменьшением размера ребра должно уменьшаться и возможное отклонение высоты его середины от среднего арифметического высот его вершин. Один из других вариантов — использовать изображения в градациях серого для карты высот. (В этом случае ландшафт можно оттекстурировать с помощью соответствующей цветной картинки и линейной генерации текстурных координат). Внимание: использование NURBS возможно, но не приветствуется в силу ограниченности использования NURBS для реальных приложений. В.З. Интерактивный ландшафт 209 |
