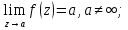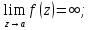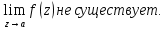курсовая ТФКП. Ряд лорана. Изолированные особые точки
 Скачать 56.74 Kb. Скачать 56.74 Kb.
|
|
ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ Кафедра математики РЯД ЛОРАНА. ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ ОГЛАВЛЕНИЕВВЕДЕНИЕ 2 ГЛАВА I. РЯД ЛОРАНА 4 1.1.Определение ряда Лорана и его область сходимости 4 1.2.Теорема Лорана 6 1.3.Изолированные особые точки 11 ГЛАВА II. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ТЕОРЕМЫ ЛОРАНА 13 2.1. Разложение аналитической функции в ряд Лорана 13 2.2. Определение характера особых точек 15 ЗАКЛЮЧЕНИЕ 18 СПИСОК ЛИТЕРАТУРЫ 19 ВВЕДЕНИЕОсновы теории функций комплексной переменной (ТФКП) были заложены в середине XVIII века Л. Эйлером, а как самостоятельная ветвь математики дисциплина оформилась около середины XIX века благодаря работам О. Коши, К. Вейерштрасса, Ю. В. Сохоцкого и Б. Римана. Сейчас ТФКП является одним из важнейших разделов математики. Ее идеи и результаты проникли во многие другие математические дисциплины, такие как алгебраическая топология, обыкновенные дифференциальные уравнения, математическая физика, функциональный анализ, теория вероятностей, вычислительная математика и др. Методы ТФКП стали привычными и в ряде прикладных дисциплин. В связи с этим курс ТФКП является обязательным на всех отделениях механико-математического, физического и геологического факультетов. В этом заключается актуальность данной работы. Целью нашей работы является изучение ряда Лорана и изолированных особых точек. Объектом данной курсовой работы является теория функций комплексной переменной. Предмет исследования: ряд Лорана, изолированные особые точки. Задачи:
Методы исследования:
Структура работы: Курсовая работа состоит из введения, двух глав, заключения, списка литературы. ГЛАВА I. РЯД ЛОРАНА
Определение: Ряд вида 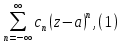 где а – фиксированная точка комплексной плоскости, 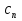 - фиксированная плоскость заданные комплексные числа, называется рядом Лорана. Ряд Лорана называется сходящимся в точке - фиксированная плоскость заданные комплексные числа, называется рядом Лорана. Ряд Лорана называется сходящимся в точке 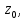 если в этой точке одновременно сходятся ряды если в этой точке одновременно сходятся ряды 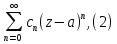 и 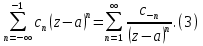 Сумма ряда (1) в точке 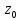 по определению равна сумме рядов (2) и (3). по определению равна сумме рядов (2) и (3).Таким образом, ряд Лорана состоит из двух рядов с коэффициентами 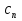 (n≥0 иn<0). Первый из них есть степенной ряд и, следовательно, его область сходимости есть круг (n≥0 иn<0). Первый из них есть степенной ряд и, следовательно, его область сходимости есть круг 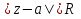 . Второй становится степенным рядом, если сделать замену . Второй становится степенным рядом, если сделать замену 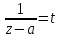 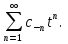 Область сходимости полученного ряда есть круг 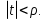 Следовательно, ряд (3) сходится в области Следовательно, ряд (3) сходится в области 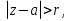 где где 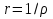 [8]. [8].Согласно нашему определению сходимости ряда Лорана, он будет обладать непустой областью сходимости в виде кругового кольца 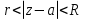 при условии 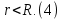 Заметим, что по формуле Коши-Адамара 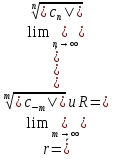 Если 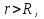 то ряд Лорана не обладает, областью сходимости. Если то ряд Лорана не обладает, областью сходимости. Если 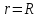 , то ряд Лорана может иметь точки сходимости, не образующие открытого множества, а расположенные на окружности , то ряд Лорана может иметь точки сходимости, не образующие открытого множества, а расположенные на окружности 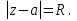 Из теоремы Абеля для степенных рядов при условии Из теоремы Абеля для степенных рядов при условии 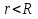 следует, что во всяком замкнутом кольце следует, что во всяком замкнутом кольце 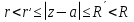 ряд Лорана (1) сходится абсолютно и равномерно, а его сумма ряд Лорана (1) сходится абсолютно и равномерно, а его сумма 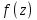 аналогичная в области сходимости аналогичная в области сходимости 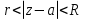 . Всюду в дальнейшем, говоря о рядах Лорана, мы всегда будем предполагать, что выполнено условие (4), без которого не существует области сходимости ряда [4]. . Всюду в дальнейшем, говоря о рядах Лорана, мы всегда будем предполагать, что выполнено условие (4), без которого не существует области сходимости ряда [4].Ряд  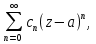 называется правильной частью ряда Лорана для функции 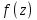 , а , а 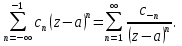 - главной частью. Ряд Тейлора является частным случаем ряда Лорана, когда в последнем отсутствует ряд (3) 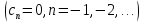 , то есть главная часть [1]. , то есть главная часть [1].
Теорема. Любую функцию 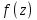 аналитическую в кольце аналитическую в кольце 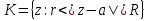 , где , где 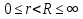 можно в этом кольце представить как сумму сходящегося ряда можно в этом кольце представить как сумму сходящегося ряда 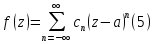 с коэффициентами 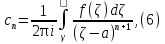 где 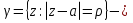 окружность произвольного радиуса окружность произвольного радиуса 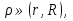 лежащего в лежащего в 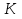 , причем в любой замкнутой подобласти , причем в любой замкнутой подобласти 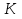 ряд Лорана (5) сходится к ряд Лорана (5) сходится к 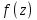 равномерно. равномерно.Заметим, что в условиях этой теоремы кольцо может вырождаться в круг с выколотым центром 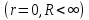 , во внешность круга с выколотой бесконечно удаленной точкой , во внешность круга с выколотой бесконечно удаленной точкой 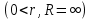 и, наконец, во всю плоскость с двумя выколотыми точками и, наконец, во всю плоскость с двумя выколотыми точками 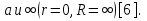 Доказательство. Рассмотрим кольцо 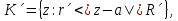 где где 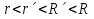 , целиком лежащее в , целиком лежащее в 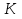 . Обозначим окружности, ограничивающие кольцо . Обозначим окружности, ограничивающие кольцо 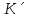 , через , через 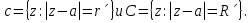 Поскольку функция Поскольку функция 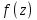 аналитическая в аналитическая в 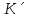 и на ее граничных контурах и на ее граничных контурах 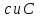 , то мы можем воспользоваться интегральной формулой Коши. Итак, , то мы можем воспользоваться интегральной формулой Коши. Итак, 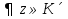 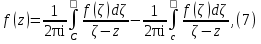 где обе окружности 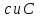 проходятся против часовой стрелки. проходятся против часовой стрелки.Аналогично доказательству теоремы о предоставлении аналитической функции рядом Тейлора, представим дробь 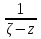 в виде суммы геометрической прогрессии в виде суммы геометрической прогрессии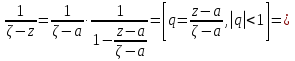 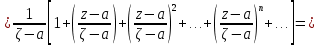 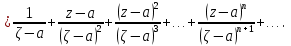 Этот ряд сходится равномерно относительно 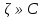 , поскольку для всех точек , поскольку для всех точек 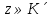 модуль модуль 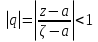 для всех точек для всех точек 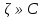 сразу. Так как функция сразу. Так как функция 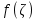 непрерывна на С, то она ограничена на С. Отсюда следует, что ряд непрерывна на С, то она ограничена на С. Отсюда следует, что ряд 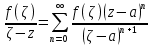 равномерно сходится по 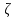 а окружности С. а окружности С.Поэтому данное равенство можно до множить на 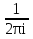 и проинтегрировать по С. Для первого интеграла (7) имеем: и проинтегрировать по С. Для первого интеграла (7) имеем: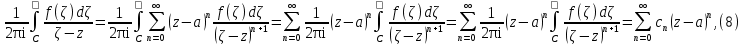 где 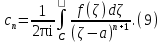 Затем, что выражение (9) нельзя представить, как в ряде Тейлора, в виде 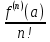 , так как , так как 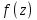 , вообще говоря, не аналитическая в точке a. , вообще говоря, не аналитическая в точке a.Перейдем ко второму интегралу из (7). Для него 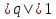 при при 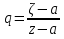 , и равномерно по , и равномерно по 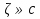 сходится прогрессия сходится прогрессия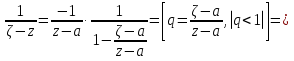 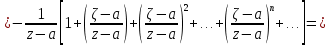 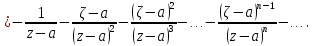 Как и выше мы можем до множить на 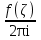 и проинтегрировать по и проинтегрировать по 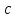 . Для второго интеграла (7) имеем: . Для второго интеграла (7) имеем: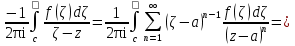 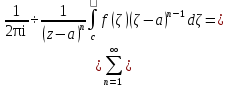 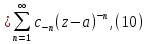 где 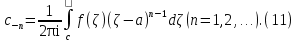 Заменим теперь в формулах (10) и (11) индекс (-n), пробегающий значения 1,2,…, индексом n, пробегающим значения -1,-2,…, получим: 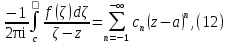 где 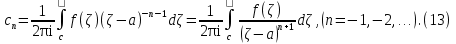 Сложим равенства (8) и (12): 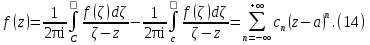 Далее, так как для произвольной окружности γ радиуса 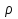 : : 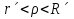 с центром в точке a, следующие три интеграла равны: с центром в точке a, следующие три интеграла равны: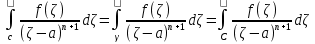 в силу интегральной теоремы Коши, то в выражениях (9) и (13) можно поменять контуры интегрирования на γ. Тогда для вычисления коэффициентов 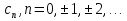 имеем общую формулу: имеем общую формулу: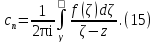 Равенства (14) и (15) и дают утверждение теоремы. Таким образом, теорема доказана. Теперь докажем единственность разложение функции в ряд Лорана [6]. Теорема. Разложение в ряд Лорана функции 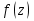 , аналитической в кольце , аналитической в кольце 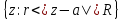 , имеет в этом кольце два разложения , имеет в этом кольце два разложения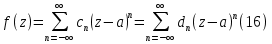 Умножаем ряды (16) на 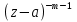 , где , где 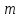 – фиксированное целое число, получаем – фиксированное целое число, получаем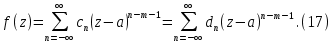 Так как ряды (17) равномерно сходятся на окружности 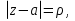 где где 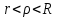 , то интегрируя их почленно по этой окружности и учитывая, что , то интегрируя их почленно по этой окружности и учитывая, что 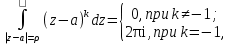 получаем 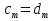 для всякого целого для всякого целого 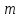 . Доказано [7]. . Доказано [7].
Определение. Точка 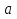 называется изолированной особой точкой функции называется изолированной особой точкой функции 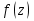 , если , если 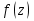 – однозначная аналитическая функция внутри кругового кольца – однозначная аналитическая функция внутри кругового кольца 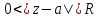 (круга с выколотым центром), а точка (круга с выколотым центром), а точка 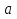 – особая точка функции – особая точка функции 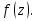 В самой точке 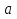 функция функция 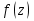 может быть не определена. может быть не определена.Поскольку выполняются условия теоремы (5), функция 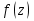 может быть разложена в окрестности точки может быть разложена в окрестности точки 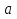 в ряд Лорана, который сходится в кольце в ряд Лорана, который сходится в кольце 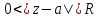 [2]. [2].При этом возможны три случая:
Указанные случаи разберем по отдельности.
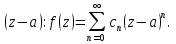 Можно доказать, что в этом случае существует предел 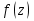 при при 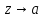 равный равный 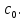 Если доопределить функцию в точке Если доопределить функцию в точке 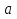 значением значением 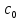 , то мы получим функцию, аналитическую в круге , то мы получим функцию, аналитическую в круге 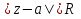 . Поэтому особые точки рассмотренного вида называют устранимыми особыми точками. Если разложение начинается с k-ой степени (k>0), то точку . Поэтому особые точки рассмотренного вида называют устранимыми особыми точками. Если разложение начинается с k-ой степени (k>0), то точку 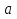 называют нулем k-го порядка функции называют нулем k-го порядка функции 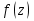 . .
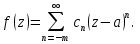 При выполнении указанного условия точку 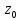 называют полюсом m-го порядка. Доказывается, что предел аналитической функции при называют полюсом m-го порядка. Доказывается, что предел аналитической функции при 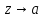 в этом случае будет равен в этом случае будет равен 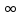 . .Легко видеть, что функция 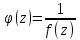 в точке в точке 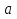 в первом случае будет иметь полюс k-го порядка, а во втором – ноль m-го порядка. в первом случае будет иметь полюс k-го порядка, а во втором – ноль m-го порядка.
Поведение функции в окрестности существенно особой точки описывается теоремой: Теорема. Для любого числа С и любого 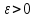 в любой окрестности в любой окрестности 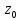 найдется точка, значение функции в которой будет отличаться от С (по модулю) меньше чем найдется точка, значение функции в которой будет отличаться от С (по модулю) меньше чем 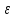 . .Для вех сформулированных утверждений верны и обратные. Поэтому часто используют геометрическую классификацию изолированных особых точек  . .Точка 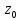 называется устранимой особой точкой, если существует конечный предел функции при называется устранимой особой точкой, если существует конечный предел функции при 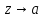 . Ряд Лорана не содержит отрицательных степеней величины . Ряд Лорана не содержит отрицательных степеней величины 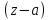 . .Точка 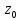 называется полюсом функции называется полюсом функции 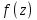 , если , если 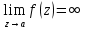 . Ряд Лорана содержит конечное число отрицательных степеней величины . Ряд Лорана содержит конечное число отрицательных степеней величины 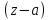 . .Точка 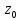 называется существенно особой точкой функции называется существенно особой точкой функции 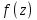 , если при , если при 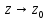 предела не существует. Ряд Лорана содержит Бесконечное число отрицательных степеней величины предела не существует. Ряд Лорана содержит Бесконечное число отрицательных степеней величины 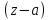 [5]. [5].ГЛАВА II. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ТЕОРЕМЫ ЛОРАНА2.1. Разложение аналитической функции в ряд ЛоранаПример 1. Разложить в ряд Лорана в кольце 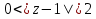 функцию функцию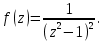 Решение. Способ 1. Функция 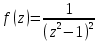 является аналитической в кольце является аналитической в кольце 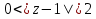 . Находим коэффициенты ряда Лорана: . Находим коэффициенты ряда Лорана: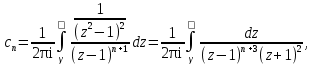 где γ – любая окружность с центром в точке 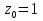 , лежащая в данном кольце. , лежащая в данном кольце.Если 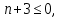 т.е. т.е. 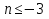 , то подынтегральная функция , то подынтегральная функция 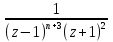 будет аналитической во всех точках внутри γ, включая точку будет аналитической во всех точках внутри γ, включая точку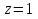 . В этом случае . В этом случае 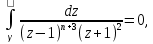 т.е. 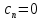 при при 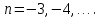 Если Если 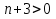 , т.е. , т.е. 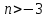 , то, применяя формулу для производной любого порядка от аналитической функции, получим , то, применяя формулу для производной любого порядка от аналитической функции, получим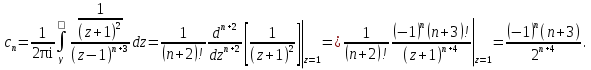 Таким образом, для 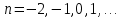 имеем имеем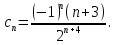 Ряд Лорана для функции 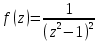 в кольце в кольце 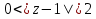 , будет иметь вид , будет иметь вид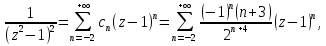 или 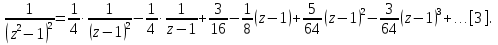 Способ 2. Преобразуем данную функцию следующим образом: 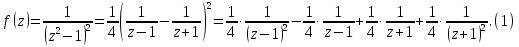 Последние два слагаемых запишем в виде 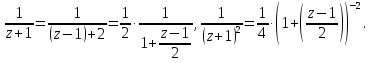 Применяя разложение по степеням 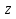 для функции для функции 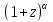 при при 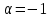 и и 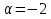 , получим , получим 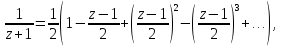 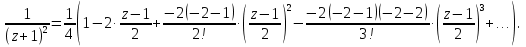 Подставляя полученные разложения в (1), найдем 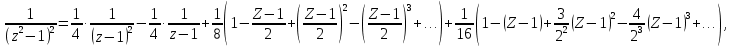 или 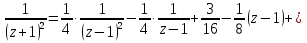 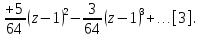 2.2. Определение характера особых точекПример. Указать, какие особые точки и какого типа имеют функции: №1. 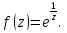 Решение. Данная функция может иметь особую точку только при 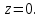 Разложение Лорана в окрестности этой точки получается, если во всюду сходящимся ряде Разложение Лорана в окрестности этой точки получается, если во всюду сходящимся ряде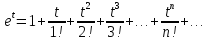 положить 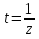 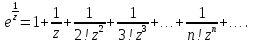 Этот ряд сходится в любой окрестности точки 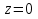 и содержит бесконечно много отрицательных степеней и содержит бесконечно много отрицательных степеней 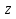 . Отсюда, по определению, следует, что . Отсюда, по определению, следует, что 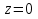 – существенно особая точка для рассматриваемой функции – существенно особая точка для рассматриваемой функции 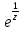 [3]. [3].№2. 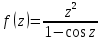 . .Решение. Особыми точками здесь будут 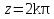 ( (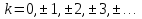 ). Точка ). Точка 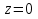 – устранимая особая точка, если положить – устранимая особая точка, если положить 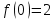 , так как , так как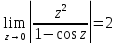 . .Точки 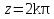 ( (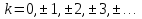 ) полюсы второго порядка, так как эти точки есть нули функции ) полюсы второго порядка, так как эти точки есть нули функции 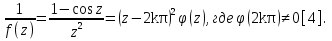 №3. 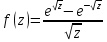 . .Решение. Замечая, что 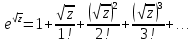 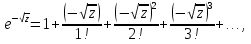 получим: 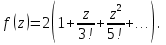 Это разложение сходится во всех точках плоскости, а потому все точки плоскости являются правильными точками для данной функции, причем точка 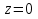 есть устранимая особая точка, если положить есть устранимая особая точка, если положить 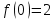 [4]. [4].№4. 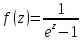 . .Решение. Особыми точками этой функции могут быть только нули знаменателя 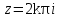 ( (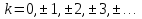 ). Если ). Если 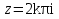 – один из этих нулей, то – один из этих нулей, то 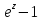 имеет следующее разложение в его окрестности: имеет следующее разложение в его окрестности: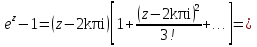 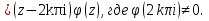 Откуда: 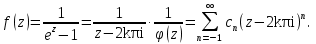 Причем 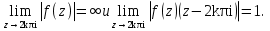 Следовательно, рассматриваемая функция имеет бесконечно много простых полюсов в точках 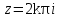 ( (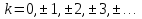 ) [3]. ) [3].ЗАКЛЮЧЕНИЕЦелью нашей работы является изучение ряда Лорана и изолированных особых точек. Мы рассмотрели методы разложения функций в ряд Лорана. Привели примеры разложения функций в ряд Лорана. А также научились определять тип изолированных особых точек и показали примеры их определения. Объектом нашей работы был курс теория функций комплексной переменной. Мы дали определение ряда Лорана: Ряд вида 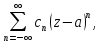 где а – фиксированная точка комплексной плоскости, где а – фиксированная точка комплексной плоскости, 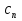 - фиксированная плоскость заданные комплексные числа, называется рядом Лорана. - фиксированная плоскость заданные комплексные числа, называется рядом Лорана.Также сформулировали теорему Лорана: любую функцию 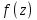 аналитическую в кольце аналитическую в кольце 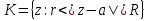 , где , где 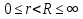 можно в этом кольце представить как сумму сходящегося ряда можно в этом кольце представить как сумму сходящегося ряда 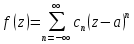 с коэффициентами с коэффициентами 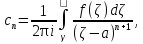 где где 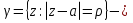 окружность произвольного радиуса окружность произвольного радиуса 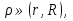 лежащего в лежащего в 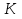 , причем в любой замкнутой подобласти , причем в любой замкнутой подобласти 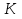 ряд Лорана сходится к ряд Лорана сходится к 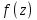 равномерно. равномерно.Исследовали типы изолированных особых точек. Изолированная особая точка 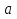 функции функции 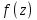 называется: называется:
Мы провели анализ методической и научной литературы по нашей теме, изучили способы разложения функций в ряд Лорана и научились определять характер особых точек. СПИСОК ЛИТЕРАТУРЫ
|