самостоятельная работа. Сам.р № 23 Физический смысл производной. С 19. Производная степени и корня

• Название: С 19. Производная степени и корня
• Анкор: самостоятельная работа
• Дата: 28.04.2023
• Размер: 88.34 Kb.
• Имя файла: Сам.р № 23 Физический смысл производной.docx
• Тип: Документы; #1096026

С -19. Производная степени и корня

Вариант 1

1)     Найдите производную функции:

1.     1) у = 3х⁴;  2) у = 2 х^{- 3};  3) у = 4 ;  4) у =   .

2.     1) у =   ;    2) у =  ;      3) у =     4) у =   .

2)    Вычислите производные при заданном значении аргумента:

1.      f(x) = 4 x³ – 3x² – x  – 1, f ^/(- 1).

2.     f(x) = (2 x³ – 1)(x² + 1), f ^/( 1).

Вариант 2

1)    Найдите производную функции:

1.     1) у = 5х³;  2) у = 3 х^{- 3};  3) у = 4 ;  4) у =   .

2.     1) у = -   ;    2) у =  ;      3) у =     4) у =   .

2)    Вычислите производные при заданном значении аргумента:

1.      f(x) = 3 x⁴ – 2x² + 4x  – 1, f ^/(- 1).

2.     f(x) = (3 x³ +1)(x³ -  1), f ^/( - 1).

C -20. Производная сложной функции

Вариант 1.

1).  Найдите производную функции:

1.1) у = (х² + 5x + 8)⁶ ;  2) у =    .

2). Вычислите производные при заданном значении аргумента:

1. f(x) =  ²,   f ^/(  ).

2. f(x) = x ,       f ^/( ).

3. f(x) =  f ^/(  ).

4. f(x) =   ,           f ^/(  ).  

Вариант 2.

1).  Найдите  производную функции:

1. у = (х³ - 4x² + 3)⁷ ;  2) у =    .

2). Вычислите производные при заданном значении аргумента:

1. f(x) = ,    f ^/(  ).

2. f(x) = x² ,       f ^/(1).

3. f(x) =  f ^/(  ).

4. f(x) =   ,           f ^/(  ).  

C - 21. Производные тригонометрической, логарифмической и показательной функций:

Вариант 1

Вычислите производные при данном значении аргумента: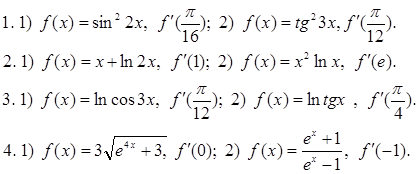



Вариант 2

Вычислите производные при данном значении аргумента: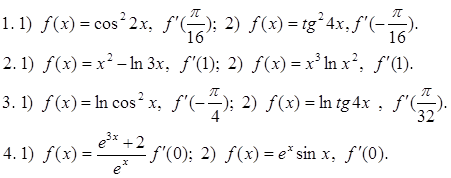



 


С - 22. Геометрический смысл производной

Вариант1

1.     Найдите интервалы возрастания и убывания функции:

1)     y = x⁴ - 4x + 4;   2) y = x³ - 6x² + 4;  

2.     Исследуйте на максимум и минимум функции:

1)    y = -  x² + 5x – 4;  2) y = 1/3 x³ - x² – 3x + 1/3;  

3.     Найдите наибольшее и наименьшее значения функции на данном отрезке:

1)    y = x² - 6x + 4;  0 ≤ x ≤ 5 ;

2)    y =  1/2 x² – 1/3 x³ ;  1 ≤ x ≤ 3;

4.     Составьте уравнение касательной к параболе

y = x² - 7x + 10 в точке х = 4; 

5.     Каким должен быть прямоугольник наибольшей площади, который можно согнуть из куска проволоки длиной 50 см.
Вариант2

1. Найдите интервалы возрастания и убывания функции:

1)     y = x² - 8x + 12;   2) y = - 1/4x⁴ - x - 1;  

2.   Исследуйте на максимум и минимум функции:

1)    y =   x² - 8x + 12;  2) y = 1/3 x³ + 1/3 x² – 2x - 1/3;  

3.   Найдите наибольшее и наименьшее значения функции на данном    отрезке:

1) y = x² - 8x + 4;  - 2 ≤ x ≤ 5 ;

2) y =  - x² + 9x³ – 24 x + 10;  0 ≤ x ≤ 3;

4.   Составьте уравнение касательной к параболе

y = x² - 6x + 8 в точке х = 5; 

5.     Каким должен быть прямоугольник наибольшей площади, который можно согнуть из куска проволоки длиной 100 см.
C - 23. Физический смысл производной

Вариант 1

1.     Точка движется прямолинейно по закону

s = 2t³ + t² – 4.

Найдите скорость и ускорение в момент времени t = 4 c.

2.     Точка движется прямолинейно по закону s = t² – 8 t + 4.

В какой момент времени скорость точки окажется равной нулю?

3.     Тело массой 10 кг движется прямолинейно по закону

 s = 3t² + t + 4. Найдите кинетическую энергию тела (mv²/2) через 4 с.

Вариант 2

1.   Точка движется прямолинейно по закону

s = t³ + 5t² + 4.

Найдите скорость и ускорение в момент времени t = 2 c.

2.   Точка движется прямолинейно по закону s = 6t –  t².

В какой момент времени скорость точки окажется равной нулю?

3.   Тело массой 100 кг движется прямолинейно по закону

 s = 5t² - 4. Найдите кинетическую энергию тела (mv²/2) через 2 с.

 

Ответы:

С-1.

B-1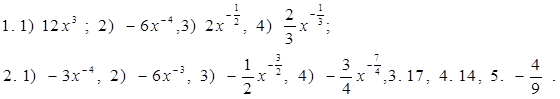 



B - 2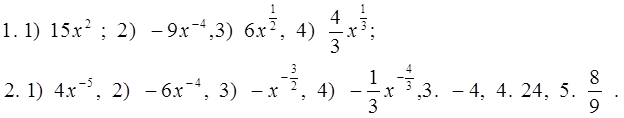



С-2

B - 1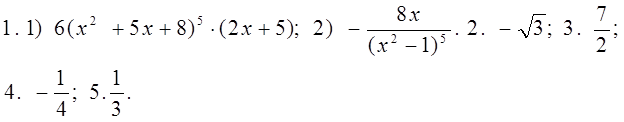



B - 2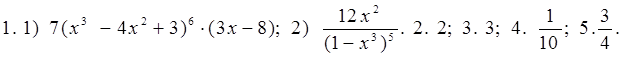

С-3

B – 1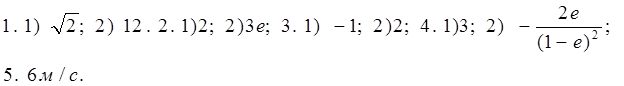



B – 2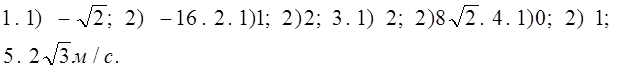



С-4

B -1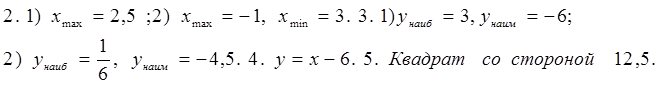





В - 2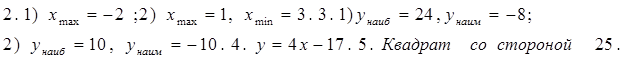





С-5

В -1



В – 2