ТЭС - пособие по курсовому проектированию.. ТЭС - пособие по курсовому проектированию. С. В. Козлов, С. С. Седов теория электрической связи
 Скачать 1.19 Mb.
|
1 2 Министерство образования Российской Федерации КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. А.Н. ТУПОЛЕВА С.В. КОЗЛОВ, С.С. СЕДОВ ТЕОРИЯ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ Пособие по курсовой работе Казань 2001 ВВЕДЕНИЕ В настоящее время наблюдается бурный рост и развитие систем связи различного назначения. Их работа обеспечивает передачу полезной информации в виде сообщений из одного пункта в другой. При передаче сообщений возникает ряд вопросов, без решения которых передача невозможна. Эти вопросы являются общими для различных систем связи и носят теоретический характер. Их изучению посвящена дисциплина «Теория электрической связи» Можно выделить следующие вопросы, относящиеся к передаче сообщений, как одни из наиболее важных: пропускная способность канала связи; верность передачи сообщений; эффективное и помехоустойчивое кодирование; оптимальный прием сигналов; цифровые методы передачи сообщений; многоканальные системы связи. Решение каждого такого вопроса составляет общую задачу, которая включает в себя ряд частных задач, различающихся в зависимости от конкретного вида передаваемого сигнала, а также от характеристик системы связи. Общей целью решения поставленных задач является уменьшение или полное устранение потерь информации при передаче сообщений с помощью системы связи. Сущность решения состоит в согласовании характеристик системы связи с передаваемыми по ней сигналами, а также в использовании методов, позволяющих принимать верное решение относительно переданной информации в условиях воздействия помех на сигнал (помехоустойчивое кодирование и статистические методы приема сигнала). Целью курсовой работы является выработка у студентов умения и навыка ставить и грамотно решать подобные задачи. В результате выполнения курсовой работы студент должен научиться рассчитывать основные характеристики элементов систем связи и уметь анализировать происходящие в них процессы. ПРАВИЛА ОФОРМЛЕНИЯ ПОЯСНИТЕЛЬНОЙ ЗАПИСКИ Объем выполняемой студентом работы: текст пояснительной записки - не менее 12 листов формата А4; графическая часть - 1 лист формата А1. Образец титульного листа приведен в приложении. Нумерация страниц пояснительной записки делается сверху, посередине листа. За титульным листом следует лист с заданием с номером 2. Первый лист с текстом будет иметь номер 3; следующий - номер 4 и т.д. Размеры полей: слева не менее 2,5 см, сверху и снизу - по 2 см, справа - не менее 1,5 см. Формулы в пояснительной записке приводятся только в отдельной строке, посередине строки. Они снабжаются номерами в круглых скобках в той же строке справа. Эти номера могут использоваться как ссылки на формулы, например: «подставляя выражение (1) в (2), получим:...». Все рисунки должны снабжаться подрисуночными подписями с номерами. Подпись ставится внизу рисунка посередине страницы, например: «Рис. 1. Структурная схема системы связи». В тексте обязательно должно быть указание на рисунок. Графики в тексте также считаются рисунками. Таблицы имеют надписи, расположенные над таблицей и прижатые к правому краю: «Таблица 1». Если таблица в тексте только одна, то номер таблицы не ставится. Используемую литературу следует привести в конце пояснительной записки по образцу, указанному в следующем разделе. В тексте необходимо делать ссылки на литературу. В квадратных скобках дается номер источника согласно приведенному списку литературы. Например: «Пропускной способностью канала связи называется [2]: (определение из литературы)». Графическая часть необходима для наглядной иллюстрации студентом рассказа о проделанной работе на защите. Она представляет собой несколько формул, таблиц и графиков, выполненных в виде рисунков на листе формата А1. Вид графического материала и его расположение на листах должны быть строго привязаны к выступлению студента на защите курсовой работы. Все представленные формулы и графики должны иллюстрировать речь студента (см. раздел «Защита курсовой работы»). Не допускается приведение на плакате каких-либо графиков или формул, если их нет в пояснительной записке. Размер элементов рисунков (букв и цифр) должен быть такой, чтобы они легко читались с расстояния 3-4 метра. Для этого высота букв и цифр должна быть не менее 3 см. Поля составляют не менее, чем по 2 см с каждой стороны листа. Структура пояснительной записки и литература Введение. Во введении кратко обосновывается актуальность поставленной задачи (ее важность и то, какими методами она решается). Также указывается место этой задачи среди общего круга задач, решаемых при передаче сообщений и результаты, к которым приводит ее решение. 2. Теоретическая часть. В теоретической части должна быть полностью раскрыта сущность решаемой задачи. Это делается на основе изучения и анализа литературы, приведенной в данном пособии. Здесь же необходимо дать определения основных понятий и величин, которые будут использоваться при решении поставленной задачи. Например, при решении задач по пропускной способности канала, нужно привести определение и формулу пропускной способности, а также тех величин, от которых она зависит и понятий, тесно связанных с пропускной способностью: полосы частот канала, отношения сигнал/шум в канале, количества информации, энтропии источника и т.д. Далее, на основании анализа задания и литературы, следует сделать качественный вывод, что при увеличении количества передаваемой информации данный канал сможет пропускать ее без искажений только до какого-то предела. При превышении этого предела необходимо либо изменять характеристики канала связи, либо применять методы т.н. «обмена» полосы частот на длительность сигнала или динамического диапазона на полосу частот, т.е. подстраивать передаваемый сигнал под данный канал. Точно такой же анализ и выводы необходимо сделать и при решении других типов задач. Результатом теоретической части должен быть выбор и обоснование расчета, необходимого для решения поставленной задачи. 3. Расчет (практическая часть). По своей сути это и есть решение задачи. Расчет выполняется по исходным данным на основании формул и соотношений, приведенных в теоретической части пояснительной записки. По результатам расчета строятся таблицы и графики, которые были указаны в задании. Делается вывод о том, при каких характеристиках сигнала и системы связи, сигнал будет передаваться данной системой без искажений. Заключение. В заключении кратко поясняется суть решенной задачи, указываются методы и способы ее решения, приводятся основные результаты. Целесообразно сделать вывод о том, что в результате проведенного расчета поставленная задача была полностью решена. 5.Литература. Образец строки в списке литературы: «1. Зюко А.Г., Кловский Д.Д. и др. Теория передачи сигналов. -М.: Радио и Связь, 1986.». Сначала проставляется номер строки, затем фамилии и инициалы авторов через запятую. Если авторов больше трех, то возможно сокращение «и др.». Далее следует название книги, город издания, название издательства, и год издания. Для Москвы и Санкт-Петербурга применяются сокращения: «-М.; -СПб». В тексте обязательно должны быть ссылки на литературу, указанную в конце настоящего пособия. В [1] дана теория по предлагаемым темам (задания 1-20); в [1 и 2] - основные формулы для этих заданий, также в [2] приведены алгоритмы помехоустойчивого и эффективного кодирования; в [3] - алгоритмы принятия статистических гипотез по критериям максимального правдоподобия, максимума апостериорной вероятности и минимума среднего риска; в [4] - формулы законов распределения вероятностей, а также понятия вероятности и плотностей распределения вероятностей; в [5] ??? в [6]. ПОРЯДОК И СРОКИ ВЫПОЛНЕНИЯ КУРСОВОЙ РАБОТЫ В течение трех первых недель осеннего семестра (до 21 сентября) студент должен получить у преподавателя задание на выполнение курсовой работы. Далее в проектный день преподаватель назначает время проведения консультаций. Регулярное посещение консультаций значительно упростит и облегчит работу. На консультациях студент решает с помощью преподавателя вопросы, возникшие у него в ходе работы над работой. Порядок работы. Первый этап. Студент по приведенной литературе должен изучить ту область, в которой он будет решать поставленную задачу. Например, если дана задача по помехоустойчивому кодированию, то студент должен представлять себе ясно и четко, что такое кодирование вообще, виды помехоустойчивых кодов, их параметры. На это при нормальном темпе работы уходит от двух недель до 1 месяца. Срок окончания первого этапа работы - 20 октября Второй этап. Студент непосредственно решает поставленную перед ним задачу. Проводит все необходимые вычисления, строит таблицы результатов и графики по ним. На это также затрачивается от двух недель до 1 месяца. Срок окончания второго этапа - 20 ноября. Третий этап работы - оформление пояснительной записки и графического материала - от одной до двух недель. Срок окончания - 5 декабря. ЗАЩИТА КУРСОВОЙ РАБОТЫ Защита курсовой работы по дисциплине «Теория электрической связи» проходит на кафедре. Защиту проводит комиссия из двух преподавателей кафедры. По результатам защиты выставляется оценка. На защите студент произносит речь, в которой он должен кратко охарактеризовать поставленную задачу, пояснить методы решения задачи и представить полученные результаты. Затем он отвечает на вопросы преподавателей, после чего комиссия выставляет оценку. Речь должна быть краткой - не более 3 минут. Студент должен четко сформулировать поставленную в работе задачу, рассказать о методах ее решения и пояснить полученные результаты. Для этого необходимо написать и выучить речь перед зашитой. На вопросы преподавателей после выступления следует отвечать более подробно и обстоятельно. Графический материал должен служить иллюстрацией к речи, т.е. на плакат следует выносить те формулы, графики и цифры, о которых студент будет рассказывать в своей речи. Пример расположения графического материала. Сначала идет общий заголовок (заголовок всей работы), затем формулы и цифры, выражающие исходное задание. Формулы даются без пояснений, все пояснения к ним делаются устно. Далее следуют формулы и таблицы основного расчета, например: «Расчет обнаруживающей и исправляющей способности помехоустойчивого кода» и приводятся основные формулы расчета и таблица расчета. Здесь тоже присутствуют только цифры. Затем следуют графики и таблицы с основными результатами работы. Графики снабжаются заголовком: «Зависимость (величины Y) от (величины X)». Затем приводятся полученные результаты в виде цифр и делаются выводы по проделанной работе. Выводы на листе даются в форме предложений, но их надо строить так, чтобы в них было как можно меньше слов. ТЕМЫ КУРСОВЫХ РАБОТ И ЗАДАНИЯ ПО НИМ ТЕМА 1. Эффективное кодирование. Коды Хаффмена и Шеннона-Фано. Задание № 1 Источник сообщений выдает целые значения xi (i=1,2,...12) случайной величины Х, распределение которой подчиняется закону Пуассона с параметром =1. Закодировать сообщения кодом Хаффмена. Определить: Пригодность кода для передачи сообщений в смысле их однозначного декодирования. Степень сжатия кода по сравнению с равномерным двоичным кодом (в процентах). Насколько код Хаффмена длиннее оптимального (в процентах). Задание № 2 Источник сообщений выдает целые значения xi (i=1,2,...10) случайной величины Х, распределение которой подчиняется закону Рэлея с параметром =2.5 Закодировать сообщения кодом Хаффмена. Определить: Пригодность кода для передачи сообщений в смысле их однозначного декодирования. Степень сжатия кода по сравнению с равномерным двоичным кодом (в процентах). Насколько код Хаффмена длиннее оптимального (в процентах). Задание № 3 Источник сообщений выдает целые значения xi (i=1,2,...12) случайной величины Х, распределение которой подчиняется закону Пуассона с параметром =3. Закодировать сообщения кодом Шеннона-Фано. Определить: Пригодность кода для передачи сообщений в смысле их однозначного декодирования. Степень сжатия кода по сравнению с равномерным двоичным кодом (в процентах). Насколько код Шеннона-Фано длиннее оптимального (в процентах). Задание № 4 Источник сообщений выдает целые значения xi (i=1,2,...10) случайной величины Х, распределение которой подчиняется закону Рэлея с параметром =4.5 Закодировать сообщения кодом Шеннона-Фано. Определить: Пригодность кода для передачи сообщений в смысле их однозначного декодирования. Степень сжатия кода по сравнению с равномерным двоичным кодом (в процентах). Насколько код Шеннона-Фано длиннее оптимального (в процентах). Задание № 5 Источник сообщений выдает целые значения xi (i=1,2,...20) случайной величины Х, распределение которой подчиняется закону Гаусса с параметрами m=10.5 и =2.5 Закодировать сообщения кодами Хаффмена и Шеннона-Фано. Определить: Какой из кодов пригоден для передачи сообщений в смысле их однозначного декодирования. Степень сжатия кодов по сравнению с равномерным двоичным кодом (в процентах). Какой из кодов оптимальнее по средней длине (в процентах). Литература по теме 1: Вентцель Е.С. Теория вероятностей. Кловский Д.Д., Шилкин В.А. Теория электрической связи. Зюко А.Г. Теория передачи сигналов. Указание. В [1] даны законы распределения случайных величин; в [2] - алгоритмы кодирования сообщений по методам Хаффмена и Шеннона-Фано; в [3] - теория эффективного кодирования. ТЕМА 2. Помехоустойчивое кодирование Задание № 6. Необходимо закодировать и передать 7 различных сообщений по двоичному симметричному каналу без памяти. Вероятность ошибки при передаче символа по каналу р=0.2. Кодирование производится избыточным кодом qи=1...4 Рассчитать в зависимости от изменения qи: d; n; r; qо кода. Вероятности ошибочного декодирования и необнаруженной ошибки. Время передачи по каналу одного сообщения, если vк=1000 сим/с. Построить графики указанных зависимостей. Задание № 7. Необходимо закодировать и передать 5 различных сообщений по двоичному симметричному каналу без памяти. Кодирование производится избыточным кодом с минимальным кодовым расстоянием по Хэммингу d=5. Вероятность ошибки при передаче символа по каналу меняется р=0.2;0.3;...0.8. Рассчитать: r; n; qи; qо кода. Вероятности ошибочного декодирования и необнаруженной ошибки в зависимости от изменения р. Время передачи по каналу одного сообщения, если vк=1000 сим/с. Построить графики указанных зависимостей. Задание № 8. Длина помехоустойчивого кода n=10. Необходимо обеспечить вероятность необнаруженной ошибки при передаче такого кода Pно<= 10-5. Вероятность ошибки при передаче символа по каналу меняется р=0.2; 0.3; 0.4, 0.5. Рассчитать: Минимальное кодовое расстояние d для каждого случая и кратность обнаруживаемых и исправляемых ошибок. Пропускную способность канала, если vк=1000 сим/с. Построить графики указанных зависимостей. Литература по теме 2: Зюко А.Г. Теория передачи сигналов. Вентцель Е.С. Теория вероятностей. ТЕМА 3. Пропускная способность канала связи Задание № 9 В канале действует аддитивный белый гауссовский шум. Отношение С/Ш меняется с 25 до 15 дБ. F=1,5 кГц; vк=7*103 бит/с Рассчитать: Изменение пропускной способности канала Изменение избыточности кода, необходимой для сведения ошибки декодирования к сколь угодно малой величине. Построить графики зависимостей С=f(Pc/Pш) и =f(С) Задание № 10 Источник сообщений выдает значения случайной величины X, подчиняющейся нормальному закону распределения с параметрами m=8.5; =2.5;3.5;...6.5. Длительность кодовой комбинации - 100 мс; vи=15 сообщ/с. Найти минимальную пропускную способность канала, при которой вероятность ошибки декодирования составит Род<10-6. Рассчитать: Изменение пропускной способности канала при изменении . Построить график зависимости С=f(). Задание № 11 Необходимо передать 105 бит информации за 70 с. Отношение С/Ш в канале - 23 дБ. Рассчитать: Ширину полосы частот канала Пусть ширина спектра передаваемых сообщений составляет 0.7 кГц, а динамический диапазон меняется от 25 до 35 дБ. Рассчитать: Изменение ширины полосы частот канала, при нулевой ненадежности передачи информации. Изменение ненадежности передачи информации при постоянной полосе частот канала, рассчитанной в первом пункте. Построить графики зависимостей F=f(PB/P); H=f(PB/P) Задание № 12 Система связи должна обеспечивать верность передачи не ниже 20 дБ. Ширина спектров передаваемых сообщений меняется от 1 до 3 кГц. Эффективность системы связи - =0.8. Рассчитать изменение минимального отношения С/Ш в канале с тем, чтобы обеспечить заданную верность. Ширина полосы частот канала - 2 кГц. Построить график зависимости. Задание №13. Эффективность системы меняется от 0.2 до 0.8. В полосе частот канала 4,5 кГц действует аддитивный белый шум, со спектральной плотностью мощности 3*10-7 Вт/Гц. Ширина спектра сообщения - 2 кГц. Рассчитать изменение минимальной мощности сигнала в канале с тем, чтобы обеспечить обобщенный выигрыш системы g’, равный трем. Построить график полученной зависимости. Литература: Зюко А.Г. Теория передачи сигналов. Кловский Д.Д., Шилкин В.А. Теория электрической связи. ТЕМА 4 Оптимальный прием сигналов Задание № 14 Необходимо с помощью метода максимального правдоподобия отыскать на участке принятого сигнала длиной 10 мс точку начала импульса. Частота дискретизации сигнала - 1 кГц. Шум распределен по закону Рэлея с =1 мВ; сигнал имеет нормальное распределение с =1 мВ m изменяется от 1 до 5.5 мВ с шагом 0.5 мВ на отсчет. Рассчитать функцию правдоподобия. Создать алгоритм поиска точки (блок-схему алгоритма). Задание № 15 Необходимо с помощью метода максимума апостериорной вероятности отыскать на участке принятого сигнала длиной 15 мс точку конца импульса. Частота дискретизации сигнала - 1 кГц. Шум распределен по закону Рэлея с =2 мВ; сигнал имеет нормальное распределение с =1,5 мВ m изменяется от 1 до 15 мВ с шагом 1 мВ на отсчет. Априорное распределение искомых точек на участке подчиняется закону Гаусса с m=5 мс от начала участка и =3 мВ Рассчитать функцию правдоподобия и апостериорную вероятность гипотез. Создать алгоритм поиска точки (блок-схему алгоритма). Задание № 16. Необходимо с помощью метода минимума среднего риска отыскать на участке принятого сигнала длиной 15 мс точку конца импульса. Частота дискретизации сигнала - 1 кГц. Шум распределен по закону Рэлея с =1 мВ; сигнал имеет нормальное распределение с =1,5 мВ m изменяется от 1 до 5 мВ с шагом 0.3 мВ на отсчет. Априорное распределение искомых точек на участке подчиняется закону Гаусса с m=8 мс от начала участка и =2 мВ. Функция потерь: 0.5*х2, где х - ошибка в мс. Рассчитать: функцию правдоподобия, апостериорную вероятность гипотез и минимум среднего риска. Создать алгоритм поиска точки (блок-схему алгоритма). Задание № 17. Принимается 2 известных сигнала от 2-х источников сообщений ИС1 и ИС2. После демодуляции и декодирования имеем: S1=5 В; S2=5.6 В. В канале действует аддитивный гауссовский шум =200 мВ. Решающее устройство анализирует принятый сигнал и определяет источник, выдавший сообщение. Априорная вероятность гипотезы о срабатывании ИС1 меняется от 0.1 до 0.9 с шагом 0.1. Рассчитать: суммарную вероятность ошибки для методов максимального правдоподобия и максимума апостериорной вероятности. Построить графики зависимостей вероятностей ошибок для 2-х методов от априорной вероятности гипотезы. Задание № 18. Принимается 2 известных сигнала от 2-х источников сообщений ИС1 и ИС2. После демодуляции и декодирования имеем: S1=7 В; S2=9 В. В канале действует аддитивный гауссовский шум =700 мВ. Решающее устройство анализирует принятый сигнал и определяет источник, выдавший сообщение. Априорные вероятности гипотез о срабатывании ИС1 и ИС2 равны 0.35 и 0.65 соответственно. Плата за риск П01=10/П10, где П10 меняется: 1; 1.3; 2; 3.16; 5; 7.5; 10. Рассчитать: суммарную вероятность ошибки для методов максимума апостериорной вероятности и минимума среднего риска. Построить графики зависимостей вероятностей ошибок для 2-х методов от платы за риск. Задание № 19. Принимается 2 известных сигнала от 2-х источников сообщений ИС1 и ИС2. После демодуляции и декодирования имеем: S1=4 В; S2=5 В. В канале действует аддитивный гауссовский шум =300 мВ. Решающее устройство анализирует принятый сигнал и определяет источник, выдавший сообщение. Априорные вероятности гипотез о срабатывании ИС1 и ИС2 равны 0.4 и 0.6 соответственно. Плата за риск П01=10/П10, где П10 меняется: 1; 1.3; 2; 3.16; 5; 7.5; 10. Рассчитать: суммарную вероятность ошибки для методов минимума среднего риска и максимального правдоподобия. Построить графики зависимостей вероятностей ошибок для 2-х методов от платы за риск. Задание № 20. На фоне аддитивной полигауссовой помехи с распределением wп(u)=q1N{m1,1}+q2N{m2,2} ведется прием полезного сигнала wc(u)=N{mc,c}. Априорная вероятность возникновения сигнала - 0.6. Решение о наличии сигнала принимается по методу максимума апостериорной вероятности. q1=0.3; q2=0.7; m1 =5В; m2, =10В; 1=2В; 2=3В mс =8В; с=1.2В. Построить графики wп и wcп и алгоритм принятия решения. Определить зоны принятия решений для методов максимального правдоподобия и максимума апостериорной вероятности. Определить суммарные ошибки для двух методов. Литература по теме 4: Левин Б.Р. Теоретические основы статистической радиотехники Т2. Зюко А.Г. Теория передачи сигналов. Вентцель Е.С. Теория вероятностей. УКАЗАНИЕ. В [1] приведены статистические методы обработки сигналов (методы максимального правдоподобия, максимума апостериорной вероятности и минимума среднего риска); в [2] дана теория оптимального приема сигналов; в [3] даны законы распределения случайных величин. ТЕМА 5: Импульсно-кодовая модуляция. Задание №21 Рассчитать систему ИКМ с равномерными дискретизацией и квантованием для пилообразного сигнала с частотой повторения 1000 Гц, динамическим диапазоном 80 дБ и максимальным значением 1В. Восстановление сигнала осуществляется фильтром второго порядка с частотной характеристикой  . Погрешность дискретизации должна составить не более 5%. Вычислить параметры фильтра RC, частоту дискретизации  , количество разрядов АЦП шум квантования и скорость передачи данных.Задание №22 Рассчитать систему ИКМ с равномерными дискретизацией и квантованием для симметричного треугольного сигнала с частотой повторения 1000 Гц, динамическим диапазоном 60 дБ и максимальным значением 1В. Восстановление сигнала осуществляется фильтром первого порядка с частотной характеристикой  . Погрешность дискретизации должна составить не более 3%. Вычислить параметры фильтра RC, частоту дискретизации , количество разрядов АЦП, шум квантования и скорость передачи данных.Задание №23 Рассчитать систему ИКМ с адаптивной дискретизацией и равномерным квантованием для гармонического сигнала с частотой 1000 Гц, динамическим диапазоном 60 дБ и максимальным значением 1В. Восстановление сигнала экстраполирующим полиномом нулевой степени. Наибольшее отклонение дискретизации  должно составить не более половины  . Вычислить моменты дискретизации в пределах периода, среднюю частоту дискретизации  , количество разрядов АЦП, шум квантования и скорость передачи данных.Задание №24 Рассчитать систему ИКМ с адаптивной дискретизацией и равномерным квантованием для гармонического сигнала с частой 1200Гц, динамическим диапазоном 50 дБ и максимальным значением 1В. Восстановление сигнала экстраполирующим полиномом первой степени. Наибольшее отклонение дискретизации должно составить не более половины . Вычислить моменты дискретизации в пределах периода, среднюю частоту дискретизации , количество разрядов АЦП, шум квантования и скорость передачи данных.Задание №25 Рассчитать систему ИКМ с адаптивной дискретизацией и равномерным квантованием для бигармонического сигнала с равноамплитудными компонентами с частотами 1000Гц и 1200Гц, динамическим диапазоном 80 дБ и максимальным значением 1В. Восстановление сигнала экстраполирующим полиномом нулевой степени. Наибольшее отклонение дискретизации должно составить не более половины . Вычислить моменты дискретизации в пределах периода, среднюю частоту дискретизации , количество разрядов АЦП, шум квантования и скорость передачи данных.ТЕМА 6: Многоканальные системы передачи информации. Задание №26 Определить ширину спектра группового сигнала 10-кагнальной системы ЧРК при условии, что каждое канальное сообщение имеет спектр сигнала постоянный в диапазоне от 0 до 3400Гц. Разделение сигналов осуществляется фильтром с АЧХ 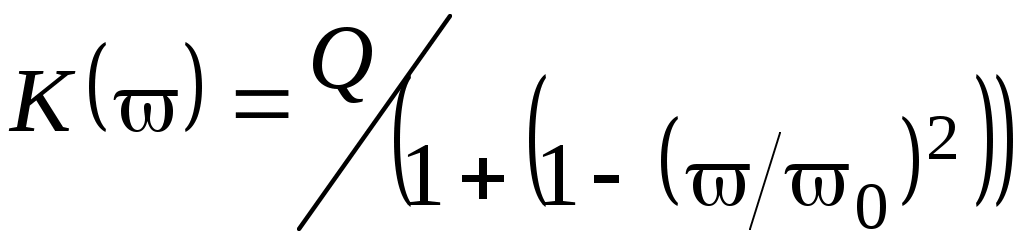 при Q=20. Уровень помех от соседнего канала не превосходит 5%.Задание №27 Определить ширину спектра группового сигнала 8-канальной системы ВРК при условии, что каждое канальное сообщение имеет спектр в диапазоне от 300 до 3400Гц, и уровень помех от соседнего канала не превосходит 5%. Задание №28 Определить ширину спектра группового сигнала системы однополосной ЧРК с коммутацией каналов при условии, что каждое канальное сообщение имеет спектр в диапазоне от 300 до 3400Гц с коэффициентом запаса 20%, интенсивностью вызова 2 за 5 с, средней продолжительностью соединения 40с и вероятностью блокировки 0,5%. Задание №29 Определить ширину спектра группового сигнала системы ВРК с коммутацией каналов при условии, что каждое канальное сообщение имеет спектр в диапазоне от 0 до 8000Гц с коэффициентом запаса 40%, интенсивностью вызова 1 за 5 с, средней продолжительностью соединения 60с и вероятностью блокировки 0,1%. ПРИМЕРЫ РЕШЕНИЯ ЗАДАНИЙ ПО ТЕМАМ ТЕМА 1. Эффективное кодирование. Коды Хаффмена и Шеннона-Фано. Задание: Источник сообщений выдает целые значения xi (i=1,2,...12) случайной величины Х, распределение которой подчиняется закону Пуассона с параметром =1. Закодировать сообщения кодом Хаффмена. Определить: Пригодность кода для передачи сообщений в смысле их однозначного декодирования. Степень сжатия кода по сравнению с равномерным двоичным кодом (в процентах). Насколько код Хаффмена длиннее оптимального (в процентах). Решение: Для создания кода Хаффмена найдем сначала вероятности, с которыми появляются 12 сообщений xi от x1 =1 до x12 =12. Закон Пуассона определяется выражением:  ; i=1,2,...12,где Pi - вероятность того, что случайная величина X примет значение, равное i. По данной формуле находим все 12 вероятностей и располагаем их в порядке убывания. Затем непосредственно кодируем сообщения кодом Хаффмена. Суть кодирования состоит в том, что мы присваиваем двум сообщениям с наименьшими вероятностями значения кодовых символов 1 и 0. Затем мы эти вероятности складываем, после чего у нас образуется новая совокупность из 11 вероятностей с одной суммарной вероятностью. Далее мы снова ищем две наименьшие вероятности и присваиваем им значения кодовых символов 1 и 0. После сложения вероятностей, их остается уже 10. Процесс кодирования продолжается до тех пор, пока не останется две суммарные вероятности. Полученный код считывается справа налево. Пример кодирования для 9 сообщений с определенными вероятностями их появления показан в таблице:
1. Пригодность кода для передачи сообщений в смысле их однозначного декодирования определяется по наличию у полученного кода т.н. префиксного свойства. Суть этого свойства заключается в том, что никакая кодовая комбинация, взятая целиком, не должна являться началом другой кодовой комбинации этого же кода. 2. Степень сжатия данного кода по сравнению с равномерным определяется так: сначала вычисляется средняя длина кодовой комбинации данного кода [2, стр. 192]:  . Минимальная длина кодовой комбинации равномерного кода, которым можно закодировать 12 сообщений определяется как наибольшее ближайшее целое к log12. Это будет 4. Таким образом степень сжатия кода можно определить:   3. Минимальная средняя долина кодовой комбинации оптимального эффективного кода численно равна энтропии источника сообщений:  .Таким образом, полученный код длиннее оптимального в процентах на:  ТЕМА 2. Помехоустойчивое кодирование Задание. Необходимо закодировать и передать 7 различных сообщений по двоичному симметричному каналу без памяти. Вероятность ошибки при передаче символа по каналу р=0.2. Кодирование производится избыточным кодом qи=1...4 Рассчитать в зависимости от изменения qи: d; n; r; qо кода. Вероятности ошибочного декодирования и необнаруженной ошибки. Время передачи по каналу одного сообщения, если vк=1000 имп/с. Решение: Сначала рассчитаем параметры кода: а) по известной кратности исправляемых ошибок qи найдем минимальное кодовое расстояние d. Известно, что qи=(d-1)/2 для нечетных d; qи=d/2-1 для четных d. Отсюда находим: d=2qи +1; или d=2(qи+1). Выберем наибольшее d. б) найдем количество избыточных символов кода r=2d-2-log(d). в) определим количество информационных символов k как наибольшее ближайшее целое к log7. Таким образом, k=3. г) найдем общую длину кодовой комбинации: n=k+r. д) обнаруживающая способность кода qо=d-1. Все эти действия необходимо проделать для различных значений исправляющей способности кода qи, изменяющейся от 1 до 4. Затем определяем вероятность ошибочного декодирования Pо.д. по формуле [1, стр. 142]:  ,и вероятность необнаруженной ошибки Pн.о.:  .Здесь [d/2] обозначает наибольшую целую часть d/2; p - вероятность ошибочной передачи одного кодового символа; Cnq - количество сочетаний из n элементов по q:  Время передачи по каналу одного сообщения T определяется так. Если известно количество кодовых импульсов, передаваемых в секунду vк, то время передачи одного импульса: 1/vк. Длина нашего кода - n импульсов. Поэтому: T=n/vк ТЕМА 3. Пропускная способность канала связи Задание В канале действует аддитивный белый гауссовский шум. Отношение С/Ш меняется с 25 до 15 дБ. F=1,5 кГц; vк=7*103 бит/с Рассчитать: Изменение пропускной способности канала Изменение избыточности кода, необходимой для сведения ошибки декодирования к сколь угодно малой величине. Решение: Пропускная способность гауссовского канала определяется [1, стр.118]:  .Отношение сигнал/шум падает по условию задания с 25 до 15 дБ. Поэтому С также будет уменьшаться. Необходимо уменьшать С/Ш с 25 до 15 дБ с шагом 1 дБ и вычислить по формуле 10 значений С. При этом надо учесть, что в формуле отношение С/Ш - Pc/Pш - дано в разах, поэтому данные в дБ необходимо пересчитать в разы:  ; отсюда  .Производительность кодера H’(B)=vк*H(B) должна быть меньше пропускной способности канала С, иначе неизбежны потери информации в канале. Максимальное значение энтропии двоичного кодера Hmax=H(B)=log2=1 бит. Если С уменьшается, то для избежания потерь информации можно уменьшать H(B) так, чтобы H’(B) оставалась все время меньше С. Если же H(B)<1, это означает, что кодовые символы не равновероятны и зависимы друг от друга, т.е. используется избыточный (помехоустойчивый) код. Избыточность этого кода вычисляется по формуле:  .Итак, пропускная способность канала С определяет предельное значение производительности кодера H’(B): H’(B)  Затем вычисляем избыточность кода . По сути эта величина показывает процент кодовых символов, которые не тратятся на передачу полезной информации а служат для защиты кода от ошибок. ТЕМА 4 Оптимальный прием сигналов Задание Принимается 2 известных сигнала от 2-х источников сообщений ИС1 и ИС2. После демодуляции и декодирования имеем: S1=5 В; S2=5.6 В. В канале действует аддитивный гауссовский шум =200 мВ. Решающее устройство анализирует принятый сигнал и определяет источник, выдавший сообщение. Априорная вероятность гипотезы о срабатывании ИС1 меняется от 0.1 до 0.9 с шагом 0.1. Рассчитать: суммарную вероятность ошибки для методов максимального правдоподобия и максимума апостериорной вероятности. Построить графики зависимостей вероятностей ошибок для 2-х методов от априорной вероятности гипотезы. Решение. Пример сигнально-шумовой ситуации, характерной для данного задания приведен на рисунке. Точки на оси U, соответствующие пикам (максимумам) кривых плотностей вероятностей w1(U) и w2(U), являются значениями сигналов S1 и S2 соответственно. Если бы на сигналы не накладывался шум, то на вход приемника поступали бы только эти два значения: либо S1, либо S2. Однако в канале действует случайный гауссовский шум n с математическим ожиданием m=0 и среднеквадратическим отклонением . Шум складывается с сигналом и поэтому невозможно заранее предсказать какое значение входного колебания Z будет на входе приемника: либо Z=S1+n,либо Z=S2+n. 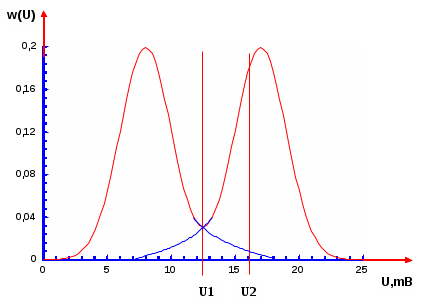 Рис.1. Сигнально-шумовая ситуация и порог принятия решения. Нормальный (гауссовсий) закон распределения шума определяется его плотностью вероятности:  При наличии только шума m=0. При складывании шума с детерминированным сигналом, мат. ожидание результирующей случайной величины Z становится равным значению сигнала: m1=S1 и m2=S2. Эти две кривые w1 и w2 изображены на рисунке. Решающее устройство определяет какой сигнал пришел на вход по порогу U1 или U2. Если значение Z<U1, то на входе имеем сигнал S1; если же Z>U1 - то сигнал S2. Порог выбирается по простому принципу: вся область значений сигнала U разбивается на две подобласти; в левой сигнал Z ближе по какому-либо критерию к S1, в правой - к S2. Критерии же эти могут быть различны. Рассмотрим сначала критерий максимального правдоподобия. Составляют так называемое отношение правдоподобия  и сравнивают его с порогом: если >1 то это сигнал S2; если <1то сигнал S1. Порог, выставленный по этому критерию показан на рисунке (U1). Критерий максимума апостериорной вероятности отличается тем, что в нем учитываются не равные вероятности гипотез о возникновении сигналов S1иS2. Здесь то же отношение правдоподобия сравнивается с порогом P(S1)/P(S2). Поэтому пороговое значение может быть другим, например как U2 на рисунке. В задании необходимо найти по известным w1 и w2 пороговое значение U1 для первого критерия, а затем рассчитать пороговые значения U2 для второго критерия, при изменяющихся значениях P(S1).При этом учесть, что P(S2)=1-P(S1). Суммарная вероятность ошибки вычисляется по формуле: 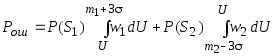 .По сути это вычисление площадей «хвостов» кривых w1 и w2, заходящих за порог U, и взятых с весовыми коэффициентами P(S1)иP(S2). Для критерия максимального правдоподобия надо принять P(S1)=P(S2). Рассчитав вероятности ошибок для различных случаев мы увидим, что максимальное значение вероятности ошибки будет получаться для критерия максимального правдоподобия. ТЕМА 5. Импульсно-кодовая модуляция. В цифровых системах связи сигналы передаются с помощью импульсно-кодовой модуляции (ИКМ). Фактически ИКМ представляет собой два последовательно осуществляемых процесса дискретизация во времени и квантование по уровню. В результате данных процессов реальный аналоговый сигнал преобразуется в последовательность цифровых кодов. Рассмотрим подробнее процесс дискретизации сигнала. Основной задачей дискретизации является выделение из сигнала некоторых временных отсчетов, обеспечивающих возможность восстановления по ним реального сигнала. При этом обычно стараются либо максимально уменьшить количество отсчетов при заданной погрешности восстановления сигнала, либо наоборот минимальной погрешности восстановления - при заданном количестве отсчетов в единицу времени. Для обеспечения этих условий мы можем варьировать двумя элементами: 1.Моментами взятия отсчетов; 2.Выбором функций, которыми аппроксимируется восстановленный сигнал. По моментам взятия отсчетов, все виды дискретизации делят на равномерную и адаптивную. В качестве функций, использующихся для восстановления сигнала, применяют функции отсчетов ряда Котельникова, интерполирующие многочлены Лагранжа, экстраполирующие многочлены Тейлора и др. Теоретически, при дискретизации по теореме Котельникова, ошибка дискретизации должна быть рана нулю. Однако в связи не возможностью точно выполнить условий теоремы Котельникова все виды дискретизации имеют некоторую погрешность  >0.Основными причинами возникновения ошибок при дискретизации по Котельникову являются не выполняющееся реально условие об ограниченности сигнала частотой  и невозможность построения идеальных фильтров нижних частот (ФНЧ), для формирования функций отсчетов. Обе эти причины зависят от выбора частоты дискретизации , причем, чем больше , тем меньше погрешность дискретизации, но тем больше объем данных передаваемых системой ИКМ за единицу времени.Относительная точность воспроизведения сигнала за счет превышения полосы реального сигнала частоты 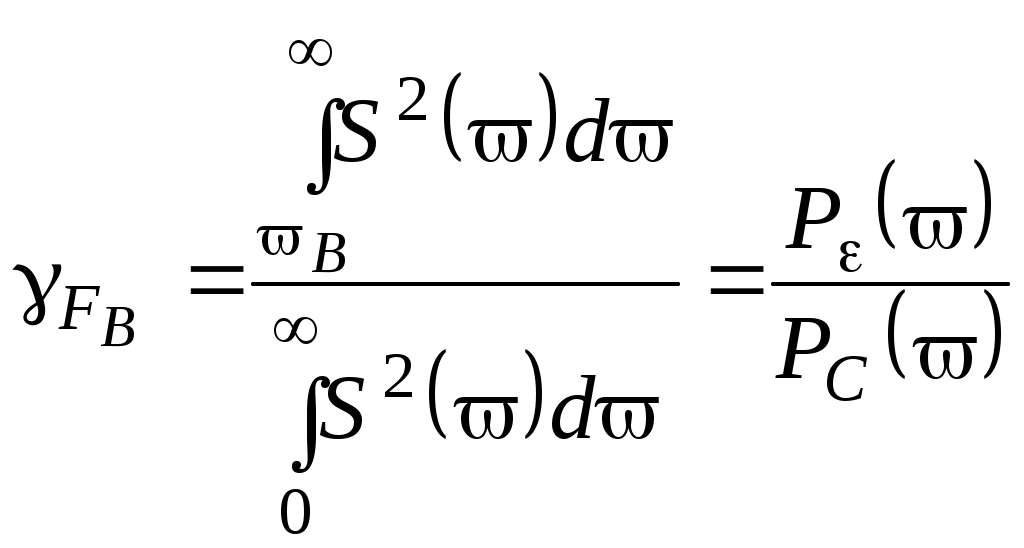 может быть определена из соотношения: ,где  - спектр входного сигнала;  - циклическая частота: .Погрешность восстановления сигнала за счет неидеальности применяемого ФНЧ 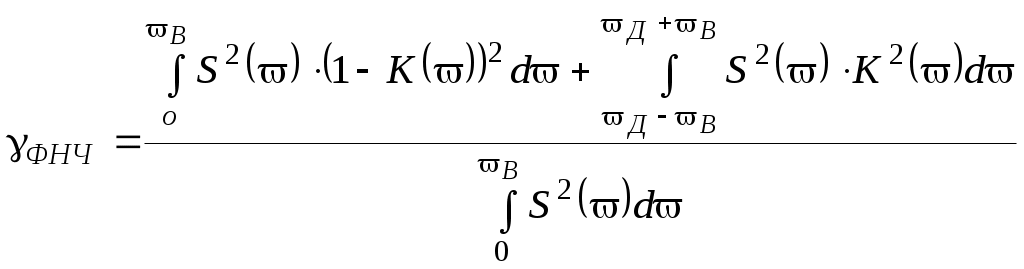 может быть определена из соотношения ,где  - частотная характеристика ФНЧ.Другим критерием качества дискретизации является критерий наибольшего отклонения . При этом оценивается погрешность восстановления , равная разности реального сигнала  и восстановленного сигнала  . Шаг дискретизации выбирают исходя из условия .Данный критерий наиболее часто применяют при адаптивной дискретизации. В этом случае время для каждого отсчета выбирают из условия  При адаптивной дискретизации наиболее часто используют метод экстраполяции сигнала многочленами Тейлора нулевой и первой степеней. Для этого многочлен определяют следующим образом:  ,где u(t) - текущее значение сигнала; u(t0) - значение сигнала в момент взятия предыдущего отсчета; u1(t0),... un(t0) - производные сигнала в момент взятия предыдущего отсчета. Примерно аналогичные преобразования с сигналом, но в амплитудной области происходят и при следующем процессе обработке – квантовании. Процесс квантования заключается в разбивании непрерывного диапазона значений сигнала от до  на n интервалов, называемых шагом квантования. При этом реальному значению аналогового сигнала ставится в соответствие номер интервала, в который попадает значение входного сигнала. Если шаг квантования постоянен, то такое квантование называют равномерным, в противном – неравномерным. Процесс квантования осуществляется в аналогово-цифровом преобразователе (АЦП).Возникающее при квантовании округление реального значения сигнала до ближайшего вызывает шум квантования, значение которого зависит от шага квантования. Для равномерного квантования среднеквадратичная ошибка квантования  определяется из соотношения: ,где  - шаг квантования, n – количество шагов квантования АЦП.В реальных системах количество шагов квантования АЦП n равняется степени числа 2, из-за двоичной системы счисления, в которой работает большинство АЦП. При этом из условия  получим формулу для определения разрядности АЦП .При получении дробных результатов величина округляется в большую сторону. Необходимая для передачи ИКМ сигнала пропускная способность канала связи определяется как произведение и   .Задание Рассчитать систему ИКМ с равномерными дискретизацией и квантованием для сигнала с верхней частотой 3400 Гц и динамическим диапазоном 40 дБ и максимальным значением 1В. Восстановление сигнала осуществляется фильтром первого порядка с частотной характеристикой . Спектр сигнала считать постоянным в диапазоне от 9 до 3400Гц. Погрешность дискретизации должна составить не более половины 5%. Вычислить параметры фильтра RC, частоту дискретизации , количество разрядов АЦП и шум квантования.Решение 1 2 |
