Контрольная работа математика 5 класс. СР 1-6_КР 1, 2. Самостоятельная работа 1 (п. 1) Вариант 1 Для данного условия задачи выберите модель, составленную с помощью таблицы

• Название: Самостоятельная работа 1 (п. 1) Вариант 1 Для данного условия задачи выберите модель, составленную с помощью таблицы
• Анкор: Контрольная работа математика 5 класс
• Дата: 28.02.2023
• Размер: 183.5 Kb.
• Имя файла: СР 1-6_КР 1, 2.doc
• Тип: Самостоятельная работа; #959756

Самостоятельная работа № 1 (п. 1.1)

Вариант 1

Для данного условия задачи выберите модель, составленную с помощью таблицы.

1. За сколько часов самолёт пролетит 1200 км, двигаясь со скоростью 120 км/ч.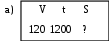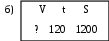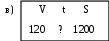



2. Решите задачу. В новом доме 206 двухкомнатных квартир, а трёхкомнатных на 48 меньше, чем двухкомнатных. Сколько всего двухкомнатных и трёхкомнатных квартир в доме?

3. Составьте модель задачи с помощью таблицы. Машина прошла расстояние между городами за 4 часа, идя со скоростью 65 км/ ч. Обратный путь она прошла за 5 часов. На сколько километров в час скорость машины на обратном пути была меньше?

4. Запишите решение задачи № 3.

5. Решите задачу, используя различные модели. Света купила несколько ручек, по 64 к. за штуку, и столько же карандашей, За ручки она уплатила 2 р. 56 к. Сколько стоили карандаши, если известно, что их цена в 4 раза меньше?
Вариант 2

Для данного условия задачи выберите модель, составленную с помощью таблицы.

1. Для ветеранов труда купили 15 тюльпанов по одинаковой цене. Какова цена тюльпана, если за покупку заплатили 45 р.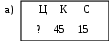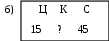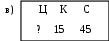


2. Решите задачу. В первый день в парке посадили 188 деревьев, а во второй – на 27 деревьев больше. Сколько деревьев посадили в парке за два дня?

3. Составьте модель задачи с помощью таблицы. Двигаясь со скоростью 18 км/ч, велосипедист проехал расстояние 108 км. Автомобилист за то же время проехал 540 км. Во сколько раз скорость автомобилиста больше скорости велосипедиста?

4. Запишите решение задачи № 3.

5. Решите задачу, используя различные модели. В швейной мастерской пошили 8 одинаковых пальто и несколько одинаковых костюмов, израсходовав 61 м ткани. На каждое пальто надо было 3 м 25 см ткани, а на каждый костюм – на 25 см больше. Сколько костюмов пошила мастерская?

Самостоятельная работа № 2 (п. 1.2 – 1.7)

Вариант 1

1. Выберите верную запись числа «семь миллионов двадцать три тысячи четыреста пять»: а) 7 230 405; б) 7 023 450; в) 7 023 405.

2. Сравните числа: а) 3 030 и 330; б) 14 479 и 14 480.

3. Выполните округление чисел до сотен: а) 8 276, б) 2 345, в) 6 980.

4. Начертите координатный луч, единичный отрезок которого равен 1 см. Отметьте на этом луче точки Т (9), К (3).Запишите длину отрезка ТК и координату точки С, если известно, что С – середина отрезка ТК.

5. Решите задачу, используя различные модели. За три дня Катя прочитала 150 страниц, причём за первые два дня ею было прочитано 97 страниц. Сколько страниц Катя прочитала в каждый их трёх дней, если во второй день она прочитала на 7 страниц больше, чем в третий?

Вариант 2

1. Выберите верную запись числа «двенадцать миллионов восемь тысяч триста четыре»: а) 12 080 304; б) 12 008 304; б) 12 008 340.

2. Сравните числа: а) 5 050 и 550; б) 23 159 и 23 160.

3. Выполните округление чисел до сотен: а) 6 448, б) 1 371, в) 5 950.

4. Начертите координатный луч, единичный отрезок которого равен 1 см. Отметьте на этом луче точки P(7), D (1).Запишите длину отрезка PDи координату точки С, если известно, что С – середина отрезка PD.

5. Решите задачу, используя различные модели. В спортзале 25 мячей: баскетбольных, волейбольных и футбольных. Футбольных мячей было на 6 больше, чем баскетбольных, а волейбольных и футбольных вместе – 18 мячей. Сколько мячей каждого вида в спортзале?

Самостоятельна работа № 3 (п. 1.8)

Вариант 1

1. Выберите верное утверждение.

Чтобы найти неизвестное уменьшаемое, надо:

а) из разности вычесть вычитаемое;

б) из вычитаемого вычесть разность;

в) к разности прибавить вычитаемое.

2. Вычислите, применяя законы сложения: 8 073 + 11 300 + 627.

3. Найдите неизвестный компонент действий:

а) 463 + b = 800; б) 2034 – n = 158; в) c – 407 = 1 093.

4. Составьте модель условия задачи и решите её, используя алгоритм решения задач «на сумму и разность».

В четвёртых и пятых классах школы 240 учащихся, причём в пятых классах на 24 ученика меньше. Сколько учащихся в четвёртых и пятых классах в отдельности?

5. Одно слагаемое увеличили на 148. Как нужно изменить второе слагаемое, чтобы сумма уменьшилась на 352?

Вариант 2

1. Выберите верное утверждение.

Чтобы найти неизвестное вычитаемое, надо:

а) к уменьшаемому прибавить разность;

б) из вычитаемого вычесть разность;

в) из разности вычесть вычитаемое.

2. Вычислите, применяя законы сложения: 5 762 + 14 200 + 38.

3. Найдите неизвестный компонент действий:

а) x + 374 = 700; б) z – 526 = 2 074; в) 2 345 – m = 678.

4. Составьте модель условия задачи и решите её, используя алгоритм решения задач «на сумму и разность».

В двух шкафах 190 книг. В одном из них на 36 книг больше, чем во втором. Сколько книг в каждом шкафу?

5. Одно слагаемое уменьшили на 316. Как нужно изменить второе слагаемое, чтобы сумма увеличилась на 208?

Самостоятельная работа № 4 (п. 1.9 – 1.10)

Вариант 1

1. Какое из следующих равенств верно:

а) 2⁵ = 5 · 5; б) 2⁵ = 2 · 2 · 2 · 2 · 2; в) 2⁵ = 2 + 2 + 2 + 2 + 2.

2. Выполните действия, соблюдая их порядок: 5² · (3³ – 9).

3. Найдите неизвестный компонент действий.

а) m · 35 = 2 380; б) 55 352 : k = 407; в) a : 43 = 86.

4. Составьте модель условия задачи и решите её, используя алгоритм решения задач на «части». Сумма двух чисел равна 306. Одно из них в 5 раз больше другого. Найдите эти числа.

5. Представьте в виде суммы разрядных слагаемых число 3 507 240, используя степени числа 10.
Вариант 2

1. Какое из следующих равенств верно:

а) 3⁴ = 4 · 4 · 4; б) 3⁴ = 3 · 4; в) 3⁴ = 3 · 3 · 3 · 3.

2. Выполните действия, соблюдая их порядок: 7² – 4³ : 8.

3. Найдите неизвестный компонент действий.

а) 45 · b = 2 790; б) x : 36 = 72; в) 67 053 : n = 309.

4. Составьте модель условия задачи и решите её, используя алгоритм решения задач на «части».Мама старше дочери в 4 раза. Сколько лет дочери и сколько лет маме, если она старше дочери на 24 года?

5. Представьте в виде суммы разрядных слагаемых число 6 407 903, используя степени числа 10.
Самостоятельная работа № 5 (п. 1.12 – 1.13)

Вариант 1

1. Какие числа являются делителями числа 24?

а) 8; б) 48; в) 6; г) 18.

2. Выпишите числа, кратные числам 20 и 30:

а) 5; б) 10; в) 60; г) 90; д) 100; е) 120.

3. Из чисел 279, 415, 732, 840, 1 107 выпишите те, которые делятся:

а) на 2; б) на 9; в) на 3 и на 5.

4. Решите задачу. Конструкторское бюро получило 108 справочников и 180 наборов карандашей, которые поровну распределили между сотрудниками. Сколько сотрудников в конструкторском бюро, если их больше 30?

5. При каком натуральном значении a значение выражения 4381 + a будет наибольшим четырёхзначным числом кратным 4?

Вариант 2

1. Какие числа являются делителями числа 15?

а) 3; б) 45; в) 12; г) 15.

2. Выпишите числа, кратные числам 8 и 12:

а) 4; б) 16; в) 24; г) 36; д) 48; е) 60.

3. Из чисел 279, 415, 732, 840, 1 107 выпишите те, которые делятся:

а) на 9; б) на 5; в) на 2 и на 3.

4. Решите задачу. Ученикам пятого класса раздали наборы тетрадей, в которые поровну распределили 140 тетрадей в линейку и 196 тетрадей в клетку. Сколько учащихся в классе, если их больше 20?

5. При каком натуральном значении a значение выражения 2718 + a будет наименьшим четырёхзначным числом кратным 4?

Самостоятельная работа № 6 (п. 1.14)

Вариант 1

1. Какую цифру надо поставить вместо *, чтобы число 2* было простым:

а) 3; б) 7; в) 5?

2. Составьте пары взаимно простых чисел: 15, 21, 28, 64.

3. Найдите: а) НОД (132; 462); б) НОК (132; 462).

4. Решите задачу. Для переправки через реку туристов можно посадить в лодки или по 8 человека в каждую, или по 10 человек. В том и другом случаях свободных мест не останется. Каково наименьшее возможное число туристов?

5. Число яблок в корзине меньше 50. Яблоки можно разделить поровну между 2, 3 и 5 детьми, но нельзя разделить поровну между 4 детьми. Сколько яблок в корзине?
Вариант 2

1. Какую цифру надо поставить вместо *, чтобы число 3* было простым:

а) 3; б) 7; в) 5?

2. Составьте пары взаимно простых чисел: 6, 15, 22, 49.

3. Найдите: а) НОД (150; 315); б) НОК (150; 315).

4. Решите задачу. Для переправки через озеро туристов можно посадить в лодки или по 12 человека в каждую, или по 15 человек. В том и другом случаях свободных мест не останется. Каково наименьшее возможное число туристов?

5. Число яблок в корзине меньше 100. Яблоки можно разделить поровну между 2, 3, 4, 5 и 6 детьми. Сколько яблок в корзине?

Контрольная работа № 1
Вариант 1

1. Укажите вариант правильного ответа записи числа «шестьдесят четыре тысячи десять»:

а) 6 410; б) 64 100; в) 64 010; г) 6 400 010.

2. Выберите верное равенство:

а) 5² = 10; б) 5² = 7; в) 5² = 25; г) 5² = 3.

3. Запишите числа в порядке возрастания: 8475, 7010, 8459, 7001.

4. Округлите число 2 795 403 до: а) тысяч; б) наивысшего разряда.

5. Найдите делимое при делении с остатком, если частное равно 18, делитель 24, а остаток 7.

6. Найдите неизвестный компонент действий:

а) 1638 – x = 564; б) n · 12 = 4 140; в) 2 544 : m = 24.

7. Используя данные рисунка, запишите координаты точек T, M, C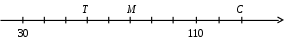


8. Найдите значение выражения: 204 · 6² + (5001 – 4³).

9. Решите задачу. Вокруг стадиона росло 32 дерева: каштаны, берёзы и липы. Каштанов было в 2 раза меньше, чем берёз, а лип — в 5 раз больше, чем каштанов. Сколько каштанов, берёз и лип росло вокруг стадиона?

10. Уменьшаемое увеличили на 126. Как нужно изменить вычитаемое, чтобы разность увеличилась на 64?

Вариант 2
1. Укажите вариант правильного ответа записи числа «семьдесят три тысячи пятьдесят»:

а) 7 350; б) 73 050; в) 73 500; г) 7 300 050.

2. Выберите верное равенство:

а) 6² = 4; б) 6² = 12; в) 6² = 8; г) 6² = 36.

3. Запишите числа в порядке возрастания: 3014, 5167, 5617, 3024.

4. Округлите число 5 678 241 до: а) сотен; б) наивысшего разряда.

5. Найдите делимое при делении с остатком, если делитель равен 13, частное 19, а остаток 5.

6. Найдите неизвестный компонент действий:

а) b – 723 = 1987; б) 16 · y = 4 112; в) p : 19 = 380.

7. Используя данные рисунка, запишите координаты точек K, N, L.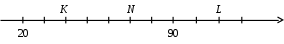


8. Найдите значение выражения: 5² · 307 + (10⁴ – 431).

9. Решите задачу. В трёх ящиках лежат 120 яблок. При этом: в первом ящике лежит в 3 раза меньше яблок, чем во втором, а в третьем – в 4 раза больше, чем в первом. Сколько яблок лежит в каждом ящике?

10. Одно слагаемое уменьшили на 316. Как нужно изменить второе слагаемое, чтобы сумма увеличилась на 208?

Контрольная работа № 2
Вариант 1

1. Выпишите уравнения:

а) 32 – 15 = 17; б) m + 3 = 0; в) 100 – x = 100; г) 60 : k; д) 9 · x = 9.

2. Выпишите пару взаимно простых чисел:

а) 16 и 20; б) 44 и 444; в) 25 и 5; г) 12 и 25.

3. Выпишите: а) делители числа 30; б) два числа, кратные 16.

4. Какие цифры надо поставить вместо *, чтобы:

а) число 21* делилось на 3; б) число *25 делилось на 9?

5. Найдите наибольший общий делитель и наименьшее общее кратное чисел по их разложению на простые множители:

m= 2 · 7 · 11; n = 2 · 3 · 7 · 11; k = 2 · 3 · 5 · 11.

6. Найдите значение выражения (29 + m) · 205 – 716 при m = 17.

7. Решите задачу с помощью уравнения.

180 разделили на задуманное число, и полученное частное уменьшили на 9. В результате получили 36. Найдите задуманное число.

8. При каком значении y значение выражения 4 · y + 2 · (y + 8) равно 64?

9. Решите задачу, используя формулы, выражающие зависимость между скоростями при движении по реке.

Скорость течения реки 5 км/ч. Катер проплыл вниз по реке 240 км за 8 ч. Какое время необходимо затратить ему на обратный путь, если собственная скорость катера не изменилась?

10. При каком натуральном значении x значение числового выражения 625 + x будет наименьшим трёхзначным числом кратным 4?
Вариант 2

1. Выпишите уравнения:

а) 32 – 15 = 17; б) m + 3 = 0; в) 100 – x = 100; г) 60 : k; д) 9 · x = 9.

2. Выпишите пару взаимно простых чисел:

а) 16 и 20; б) 44 и 444; в) 25 и 5; г) 12 и 25.

3. Выпишите: а) делители числа 28; б) два числа, кратные 18.

4. Какие цифры надо поставить вместо *, чтобы:

а) число 2*3 делилось на 3; б) число 3*7 делилось на 9?

5. Найдите наибольший общий делитель и наименьшее общее кратное чисел по их разложению на простые множители:

a= 3 · 7 · 13; b = 2 · 3 · 5 · 13; c= 2 · 3 · 7 · 13.

6. Найдите значение выражения 308 · (n + 37) – 824 при n = 28.

7. Решите задачу с помощью уравнения.

Некоторое число увеличили в 12 раз, результат вычли из 320 и получили 236. Какое число задумали?

8. При каком значении x значение выражения 5 · x + 3 · (x + 9) равно 75?

9. Решите задачу, используя формулы, выражающие зависимость между скоростями при движении по реке.

Расстояние между двумя пристанями 252 км. Теплоход прошёл это расстояние вниз по течению реки за 9 ч. Сколько времени теплоход затратил на обратный путь, если скорость течения реки 5 км/ч?

10. При каком натуральном значении x значение числового выражения 478 + x будет наибольшим трёхзначным числом кратным 4?