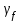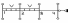РПЗС 19-5, Алибекулы Султанбек). сборные железобетонные конструкции многоэтажного здания по дисциплине Проектирование и расчет железобетонных конструкций ii
 Скачать 243.86 Kb. Скачать 243.86 Kb.
|
|
МЕЖДУНАРОДНАЯ ОБРАЗОВАТЕЛЬНАЯ КОРПОРАЦИЯ КАЗАХСКАЯ ГОЛОВНАЯ АРХИТЕКТУРНО-СТРОИТЕЛЬНАЯ АКАДЕМИЯ Факультет общего строительства ЗАДАНИЕ для выполнения курсового проекта № 1 на тему «СБОРНЫЕ ЖЕЛЕЗОБЕТОННЫЕ КОНСТРУКЦИИ МНОГОЭТАЖНОГО ЗДАНИЯ» по дисциплине «Проектирование и расчет железобетонных конструкций II Тапалов А Курс 3 Группа Стр(РПЗС)-19-5 Требуется запроектировать несущие железобетонные конструкции многоэтажного промышленного или гражданского здания. Исходные данные: Размеры здания в плане 19,8х76 мхм Сетка колонн 6,6х7,6 мхм Количество 5 и высота этажей 3,6 м Временная нормативная нагрузка на перекрытие 6,2 кН/м2 Расчетное сопротивление грунта ________________________МПа Глубина промерзания грунта 1,5 м Материалы для ригеля: бетон класса В20 арматура из стали класса А-ІІІ Материалы для других конструкции: бетон класса В25 арматура из стали класса _______________________________ Номер ID 31911297
 Расчет и конструирование сборного железобетонного ригеля Исходные данные 1. Размеры здания 19,8 х 76 мхм 2. Сетка колонн 6,6 х 7,6 мхм 3. Высота этажа 3,6м 4. Размеры сечения колонн 40х40 смхсм 5. Длина ригеля lp =7,6м 6. Расположение ригелей – вдоль поперечных осей 7. ар=7,6м 8. Класс ответственности здания γn=0,95 4.1 Определение расчетных сопротивлений арматуры и бетона Ригель изготовляется из тяжелого бетона, подвергнутого тепловой обработке при атмосферном давлении, класса В20; коэффициент условий работы бетона γb2=0,9. Rb=11,5·0,9=10,35 МПа, Rbt=1,05·0,9=0,945 МПа. Модуль упругости бетона Eb=27·103 МПа. Продольная арматура класса А-III: Rs=365МПа, Es=2,0·105 МПа. Поперечная арматура класса А-II: Rsw=280МПа, Es=2,1·105 МПа. 4.2 Установление расчетной схемы и величины пролетов ригеля Ригель рассчитывают как трехпролетную неразрезную балку. За расчетный размер пролетов ригеля принимается расстояние между осями колонн L=7,6м. 4.3 Назначение предварительных размеров поперечного сечения ригеля Для определения собственного веса ригеля задаются размерами поперечного сечения: h=(1/12)L=(1/13)760=59см. Принимаем h=60см. b=0,4∙h=0,4∙60=24см. Принимаем b=25см. 4.4 Определение расчетных постоянной и временной нагрузок на 1 погонный метр ригеля Нагрузка на ригель от панелей при числе ребер панелей в пролете ригеля более четырех считается равномерно распределенной. Подсчет нагрузок в таблице 4.1 Таблица 4.1
Расчетные нагрузки на 1м длины ригеля определяются путем умножения расчетных нагрузок на ширину грузовой площади, равной шагу ригелей: -собственный вес панели и пола: 3,6∙6,6=23,76 кН/м -собственный вес ригеля: b∙h∙∙gf=0,25∙0,6∙1∙25∙1,1=4,125 кН/м Полная постоянная нагрузка с учетом коэффициента надежности по назначению n=0,95: g = (23,76+4,125)·0,95=26,49 кН/м Временная расчетная нагрузка: v=7,44∙6,6∙0,95=46,64 кН/м Полная расчетная нагрузка: q=g+v=26,49+46,64=73,13 кН/м 4.5 Статический расчет ригеля Усилия в ригеле – изгибающий момент и поперечную силу получают в результате статического расчета, произведенного по правилам строительной механики, как упругой системы. Опорные моменты ригелей определяются по формуле, при равномерно распределенной нагрузке: 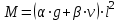 , ,где и – табличные коэффициенты, зависящие от схемы загружения ригеля нагрузками g и v, а также от отношения погонных жесткостей ригеля и стойки (колонны): 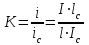 Ведем расчет ригеля крайнего пролета средней рамы, поскольку порядок расчета остальных пролетов аналогичен. Значения изгибающих моментов в средних пролетах многопролетных рам принимают по среднему пролету трехпролетной рамы. 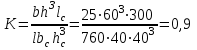 Таблица 4.2
Значения изгибающих моментов Мх в пролете на расстоянии х от левой опоры и поперечных сил Q на опорах определяются, как в балках, с учетом действительной нагрузки q и найденных по таблице опорных моментов при различных сочетаниях нагрузок: 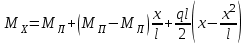 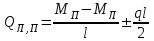 q=g+v или q=g , т.е. в зависимости от схем загружений для незагруженных пролетов должна учитываться только постоянная равномерно распределенная нагрузка. Сечение в пролете ригеля, где возникает максимальный изгибающий момент Мu, определяется из условия Qx=dMx/dx=0 и находится на расстоянии xu от левой опоры. xu=QЛ/q Таблица 4.3
Вычисленные значения поперечных сил и максимальных пролетных моментов сведены в таблице 4.4 Таблица 4.4
4.6 Перераспределение изгибающих моментов в неразрезном ригеле Усилия, полученные в результате расчета неразрезных железобетонных ригелей в предположении упругой работы материала, не всегда соответствуют действительным значениям. Поэтому их рассчитывают по методу предельного равновесия, который допускает образование в конструкции трещин и пластических шарниров в количестве, не приводящем ее в геометрически изменяемую систему, и учитывает перераспределение усилий в ней вследствие пластических деформаций материала. После появления пластического шарнира при дальнейшем увеличении нагрузки происходит перераспределение изгибающих моментов между отдельными сечениями. При этом деформации в пластическом шарнире нарастают, но значение изгибающего момента сохраняется постоянным и равно тому значению, которое было достигнуто к моменту образования шарнира. Перераспределение изгибающих моментов производится следующим образом. Построенные для невыгодных загружений эпюры моментов упругой системы выравнивают наложением на них добавочной эпюры, вызванной добавочным опорным моментом противоположного знака в пластическом шарнире. Добавочная эпюра моментов строится как для упругой системы (прямоугольная в пролете). Значение добавочного опорного момента определяется исходя из условия не увеличения расчетных значений пролетных моментов и должно составлять не более 30 % значения выравниваемого момента во избежание чрезмерного раскрытия трещин в сечении, где может образоваться пластический шарнир: 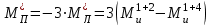 = -3(211.97-196.68)= 45,87 кНм = -3(211.97-196.68)= 45,87 кНм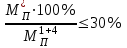 45,87*100%/386,94=11,8<30% 45,87*100%/386,94=11,8<30%где  – ординаты добавочной эпюры моментов соответственно на левой и правой опорах. – ординаты добавочной эпюры моментов соответственно на левой и правой опорах.Значения ординат добавочной эпюры в пролете определяется по следующему выражению: 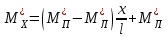 Суммирование основной и добавочной упругих эпюр дает перераспределенную эпюру. Принимая во внимание по всей длине ригеля лишь наибольшие положительные и отрицательные ординаты, получают объемлющую эпюру изгибающих моментов. Поскольку отрицательные изгибающие моменты в ригеле по мере удаления от оси опор (т.е. колонн) снижаются, в качестве расчетных опорных моментов принимают момент сил по грани колонн: 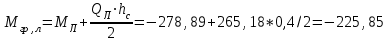 кНм; кНм; 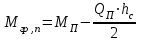 =-332,2+279,21*0,4/2= -276,36кНм =-332,2+279,21*0,4/2= -276,36кНмТаблица 4.5
По данным таблиц строятся эпюры перераспределенных усилий для различных сочетаний нагрузок и устанавливаются расчетные значения изгибающих моментов (на опорах и в пролете) и поперечных сил. Причем для расчета прочности по сечениям, наклонным к продольной оси, принимаются значения поперечных сил ригеля, большее из двух расчетов: упругого расчета и с учетом перераспределения моментов, т.е. с учетом комбинации нагрузок 1+4; а при установлении расчетных значений моментов указанная комбинация нагрузок во внимание не принимается. Значения расчетных усилий приведены в сводной таблице 4.6 Таблица 4.6
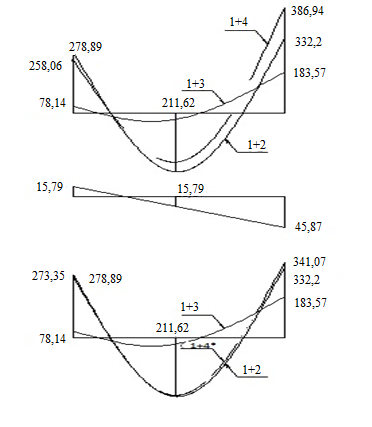 Эпюры изгибающих моментов ригеля а) основная (из упругого расчета); б) добавочная; в) перераспределенная 4.7 Уточнение высоты сечения ригеля Высота сечения ригеля определяется из условия возможного образования пластического шарнира: 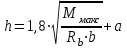 , ,где 1,8 – коэффициент, соответствующий рекомендуемому оптимальному значению относительной высоты сжатой зоны бетона.  ω= α –0,008Rb=0,85–0,008·13,05=0,7456 α=0,85 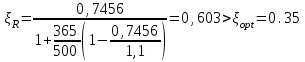 ξopt=0,35< ξR=0,5821 т.е. условие ξ ξR соблюдается 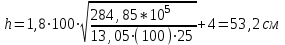 Окончательно принимаем h=60 см, b=25 см. 4.8 Расчет прочности ригеля по сечениям, нормальным к продольной оси (подбор продольной арматуры) Сечение на крайней опоре: М=225,85 кН·мРабочая высота сечения ригеля при однорядном расположении стержней: h0 = h – a = 60-4 = 56м 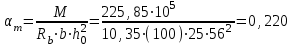 ξ=0,603< ξR=0,5821 , т.е. условие ξ ξR соблюдается 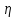 =0,87 =0,87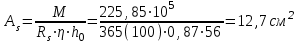 , , 325 А-III; Аs= 14,73 см2 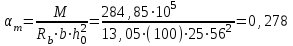 ξ=0,603< ξR=0,5821 , т.е. условие ξ ξR соблюдается 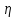 =0,83 =0,83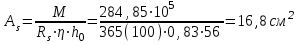 , , 328 А-III; Аs= 18,47 см2 Сечение в пролете: М=211,97 кНм Рабочая высота сечения при расположении арматуры в два ряда: 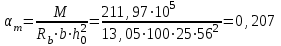 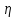 =0,88 =0,88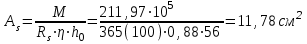 , ,325 А-III; Аs=14,73см2 Так как в пролетах отсутствуют отрицательные моменты, то верхнюю зону ригеля армируем конструктивно: 212 А-III; Аs=2,26 см2 4.9 Расчет прочности ригеля по сечениям, наклонным к продольной оси (подбор поперечной арматуры) В качестве расчетного принимаем сечение на средней опоре, в котором действует максимальная поперечная сила Qmax=289.15 кН. Выполним проверку условий, что 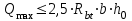 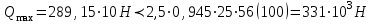 , условия выполняется , условия выполняетсяПри диаметре продольной арматуры 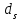 =32мм принимаем диаметр поперечных стержней из условия свариваемости =32мм принимаем диаметр поперечных стержней из условия свариваемости 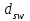 =8мм, но минимальный диаметр арматуры класса А-II равен 10мм, то окончательно принимаем =8мм, но минимальный диаметр арматуры класса А-II равен 10мм, то окончательно принимаем 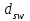 =10мм. Так как число хомутов - 3, то площадь сечения поперечных стержней равна =10мм. Так как число хомутов - 3, то площадь сечения поперечных стержней равна 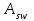 =30,785=2,355 см2 =30,785=2,355 см2 Определим шаг стержней исходя из конструктивных требований. При h450 мм sh/3=60/3=20 см и не более 500 мм. На приопорных участках равных ¼ пролета принимаем s=20 см. В средней части пролета, равной L/2 шаг поперечных стержней должны составлять s3/4h=3·60/4=45 см, но также не более 500мм. Принимаем s (1)=20 см. Тогда погонное усилие в поперечных стержнях отнесенные к единицу длины будет 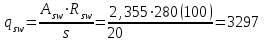 Н/см Н/смПрочность наклонного сечения обеспечена. Произведем проверку прочности наклонной сжатой полосы между наклонными трещинами: Отношение модулей упругости 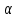 =Es/Eb=2,1·105/27·103=7,7 =Es/Eb=2,1·105/27·103=7,7Коэффициент поперечного армирования по длине μω=As/b·s=2,355/25·20=0,00471 Коэффициент, учитывающий влияние хомутов φω1=1+5·7,7·0,00471=1,181,3 Коэффициент, оценивающий способность различных видов бетона φb1=1–β Rb=1–0,01·13,05=0,869 β=0,01- для тяжелого бетона Проверка прочности по сжатой полосе между наклонными трещинами по условию 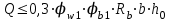 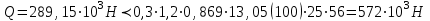 Условие выполняется, прочность обеспечивается. 4.10 Построение эпюры арматуры Эпюра арматуры – эпюра изгибающих моментов, выдерживаемых арматурой ригеля. Ординаты эпюры арматуры вычисляют как момент внутренних сил в рассматриваемом сечении ригеля 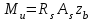 Поскольку изгибающий момент по длине пролета величина переменная, в целях экономии металла часть продольной арматуры (не более 50% расчетной площади) может обрываться в пролете по мере уменьшения момента, т.е. там, где она уже по расчету не требуется. Сечение ригеля, в котором часть арматуры по расчету уже не нужна, называется местом теоретического обрыва. Длина, на которую обрываемый стержень должен быть заведен за место теоретического обрыва: 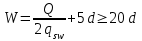 Сечение на крайней опоре 325 А-III; Аs= 14,73 см2 Высота сжатой зоны бетона 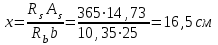 Плечо внутренней пары 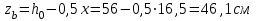 Момент, воспринимаемый сечением на опоре: 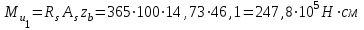 В месте теоретического обрыва арматуры диаметром 28 мм имеется конструктивная арматура 212 А-III с As=2,26 см2, для которой: 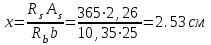 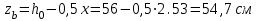 Момент, воспринимаемый сечением в месте теоретического обрыва стержней: 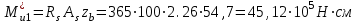 В соответствии с огибающей эпюрой моментов расчетным является сочетание нагрузок (1+2): Мл= -278,89 кНм; Мп= -332,2 кНм; Qл=265.18 кН; q=q*=71,63 кН/м; 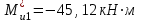 , ,где q*–интенсивность равномерно распределенной нагрузки, соответствующей принятому для определения поперечной силы сочетанию нагрузок. Тогда 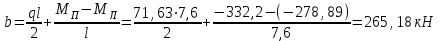 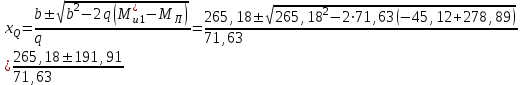  =6,38 м =6,38 м =1,02 м. Из двух решений принимаем последнего. =1,02 м. Из двух решений принимаем последнего.Расчетное значение поперечной силы в этом сечении:  кН. кН.Длина запуска стержней за место теоретического обрыва 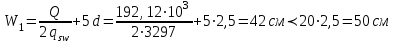 Принимаем 50 см Место практического обрыва стержней находится левее середины пролета ригеля на расстоянии: 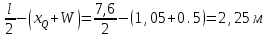 Сечение на средней опоре 328 А-III; Аs= 18,47 см2 Высота сжатой зоны бетона 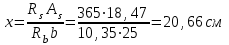 Плечо внутренней пары  Момент, воспринимаемый сечением на опоре: 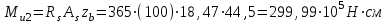  В соответствии с огибающей эпюрой моментов расчетным является сочетание нагрузок: 1+2– для определения поперечной силы; 1+3 – в соответствии с местом теоретического обрыва стержней: Мл= -78,14 кНм; Мп= -183,57 кНм; Qл=265.18 кН; q*=71,63 кН/м; q=26,49 кН/м; 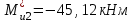 Тогда 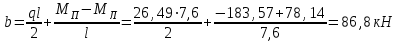   =0,4м =0,4м =6,15 м. Из двух решений, очевидно, что =6,15 м. Из двух решений, очевидно, что  =6,15 м. =6,15 м.Расчетное значение поперечной силы в этом сечении: 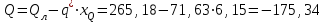 кН. кН.Длина запуска стержней за место теоретического обрыва 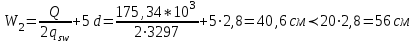 Принимаем 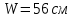 Место практического обрыва стержней находится правее середины пролета ригеля на расстоянии: 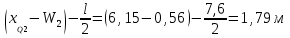 4.11 Армирование ригеля Поперечные стержни вместе с продольными образуют плоские сварные каркасы, которые объединяют в пространственные с помощью горизонтальных поперечных стержней, устанавливаемых через 1-1,5 м. Пространственная жесткость каркаса обеспечивается замкнутым контуром, а при длине ригеля более 6 м, также приваркой диафрагм жесткости в виде специальных связей из диагональных стержней, длина которых равна: 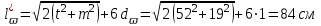 Длина элемента-вставки: lb=4·3,2=14,8<15см. Значит lb=15см. На верхней грани ригеля предусмотрены закладные детали МН1 для крепления плит покрытия. В опорных частях ригеля устанавливаются закладные детали МН2 для крепления ригелей к колоннам. Для строповки ригелей при монтаже предусмотрены 2 отверстия d=50 мм на расстоянии 1 м от концов ригеля. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

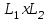 =19,8х76м
=19,8х76м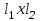 =6,6х7,6м
=6,6х7,6м