тесты физика. Физика тесты. Сборник тестов по курсу общей физики иваново 2006 удк 53 Кудин Л. С. Сборник тестов по курсу общей физики
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
КВАНТОВАЯ МЕХАНИКАПРИНЯТЫЕ ОБОЗНАЧЕНИЯ А - постоянная нормировки <A> - среднее значение величи- ны А ^p- оператор импульса p- приращение импульса A^ - оператор R- коэффициент отражения а - константа s - спиновое квантовое число электрона b - константа Т - кинетическая энергия с - скорость света, комплекс- ное число t - время D - коэффициент пропускания U - напряжение, потенциальная энергия Е - энергия V - объем е - элементарный заряд w - вероятность ^ H - гамильтониан (оператор полной энергии) u, u* - функция переменной величины ћ, h - постоянная Планка v- скорость i - мнимая единица x, y, z - координата k - постоянная Больцмана, константа l - длина, орбитальное кван- товое число электрона x^ оператор координаты Z - порядковый номер элемента в периодической таблице Д.И. Менделеева M- ^ оператор момента импуль- са - приращение, оператор Лапласа М - момент импульса - оператор Набла m - масса, целое число - длина волны, собственные зна- чения оператора mе - масса электрона v - частота, функция переменной величины m0 - масса покоя , * - волновая функция, зависящая от времени n - целое число * - плотность вероятности ^ T - оператор кинетической энергии , * - волновая функция, зависящая от координат р- импульс - частота ТЕСТОВЫЕ ЗАДАНИЯГипотеза де Бройля выражается соотношениями а) = 2ћ ; p б) E = ћ; в) = 2с; г) = En– Em . ћ Длина волны де Бройля для заряженной частицы, ускоренной электриче- ским полем, определяется по формуле p 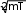 а) 2ћ; б) 2ћ а) 2ћ; б) 2ћ ; в) 2ћ ; г) 2ћ. m v  Установите соответствие между определением и его математическим вы- ражением. Установите соответствие между определением и его математическим вы- ражением.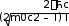 Определение Математическое выражение а) соотношение де Бройля 1) Определение Математическое выражение а) соотношение де Бройля 1)б) релятивистский импульс 2) x px ћ/2 в) связь длины волны Де Бройля с кинетической энергией в классиче- ском приближении г) связь длины волны Де Бройля с кинетической энергией в релятиви- стском случае m0v 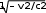 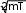 4)2ћ 4)2ћm д) соотношение неопределенностей 5) 2ћ v а) ; б) ; в) ; г) ; д) . Существование у атомов дискретных энергетических уровней было экспе- риментально установлено в опытах а) Штерна и Герлаха; б) Франка и Герца; в) Резерфорда; г) Ленарда и Томсона. Экспериментальные доказательства волновых свойств у микрочастиц бы- ли получены в опытах а) Томсона и Тартаковского; б) Франка и Герца; в) Фабриканта, Бибермана, Сушкина; г) Девиссона и Джермера. Квантование магнитных моментов атомов было экспериментально уста- новлено в опытах а) Штерна и Герлаха; б) Франка и Герца; в) Комптона; г) Девиссона и Джермера. Неопределенность в измерении энергии за данный промежуток времени равна 2 а) E=ћ; б) Et ћ; в) E= 2ћ2  ml2 n . ml2 n .Волновая функция , являющаяся решением уравнения Шредингера H^ = E , должна удовлетворять требованиям: а) функция должна быть непрерывной, однозначной и конечной; б) функция должна иметь решение при любых значениях энергии Е; в) функция должна иметь решение при собственных значениях энер- гии Е. Какое из приведенных ниже уравнений представляет временное уравне- ние Шредингера? ⎛– ћ2 2 ⎞  2 2m а) ⎜ ⎝ 2m + U⎟ ⎠ = iћ t ; б) + ћ2 (E – U) = 0 ;  в) H^ = E ; г) в) H^ = E ; г)d2 dx2 + 2mE = 0 . ћ2 В квантовой механике физическая величина характеризуется не числовым значением, а оператором. Оператор - это а) функция, которая осуществляет связь одних чисел с другими числа- ми; б) правило, с помощью которого каждой функции из некоторого мно- жества функций сопоставляется функция из того же или некоторого другого множества функций; в) числовое значение физической величины, которой ставится в со- ответствие данный оператор. Оператор A^ называется самосопряженным (эрмитовым), если для любых двух функций u и v 1 2 1 2 а) A^(au+ av) =aA^u+ aA^v; б) ⌠v*A^udV= uA^*v*dV; в) u *v dV = 0 (m n); г) u *v dV = 1 (m = n). n m n m Спектр собственных значений энергий гармонического осциллятора явля- ется а) сплошным; б) дискретным; в) смешанным. Приведите в соответствие оператору его обозначение. Оператор Обозначение а) оператор координаты 1) p^ = – iћ xx ^ – ћ2 2  б) оператор импульса 2) H= 2m + U ^ – ћ2 2  в) оператор момента импульса 3) T= г) оператор кинетической энергии 4) x^ = x 2m д) оператор полной энергии ^ ⎛ – ⎞ 5) Mx= – iћ⎜xy y ⎟ ⎝ x⎠ а) ; б) ; в) ; г) . д) . Среднее значение физической величины находится в квантовой механике по формуле n а) <A>=n⎜an⎜2; б) A^ = ; в) <A^ >= *<A^ >dV.. n n n 1 Поставьте в соответствие определению математическое выражение. Определение Математическое выражение а) плотность вероятности 1) cnn n б) условие нормировки 2) * n m в) принцип суперпозиции 3) * dV= 0 (m n) n г) ортогональность волновых функций 4) *mdV= 1 (m=n) а) ; б) ; в) ; г) . ⎛i⎞ Собственные функции (x, t) =Aexp ⎜ћ(px–Et)⎟ являются решением ⎝ ⎠ уравнения а) 2 + 2m(E – U) = 0 ; б) d2 dx2 + 2m(E – U) = 0 ;  ћ2 – ћ2 2  ћ2  d2 2m  в) 2m x2 = iћt ; г) dx2 + ћ2 E = 0 . Поставьте в соответствие конкретному условию запись уравнения Шре- дингера. Условие Уравнение а) общее уравнение Шредингера d2 ⎝  2m⎛ – m2 2⎞  dx2 + ћ2 ⎜E x ⎟ = 0 2 ⎠  ћ2 2) в) уравнение Шредингера для частицы в одномерной потенциальной яме 3) 2 + 2m(E – U) = 0 ћ2 г) уравнение Шредингера для одномер- ного гармонического осциллятора д) уравнение Шредингера для частицы, d2 dx2 +  4) – ћ2  2mE = 0 ћ2 2 движущейся в одномерном потенци- альном поле 5) 2m + U = iћt а) ; б) ; в) ; г) ; д) . Какой из приведенных на рисунке спектров энергетических уровней соот- ветствует частице в потенциальной яме?                   а) б) в) Собственные значения энергии водородоподобного атома записываются в виде  ⎝ ⎠ 2ћ2 ⎛ 1⎞ meZ2e41  k2ћ2  а) Е =2ml2 n2; б) Е=⎜n+2⎟ ћ ; в) E =– 2ћ2 n2; г) Е = 2m . Стационарное уравнение Шредингера для водородоподобного атома име- ет вид  ⎛ ћ2 ⎛ ћ2⎞ 2 2m⎛ Ze2⎞  а) ⎜– 2m2 + U⎟ = iћ ; б) + ћ2 ⎜E+ r ⎟ = 0 ; ⎝ ⎠ t d2 2m⎛ – m2 2⎞   ⎝ ⎠ d2 2m  в) dx2 + ћ2 ⎜E x ⎟ = 0; г) ⎝ 2 ⎠ dx2 + ћ2 E = 0 . 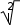 ⎛nx⎞ ⎛nx⎞Собственные функции: (x) = ния sin ⎜ l ⎝ ⎟ являются решением уравне- ⎠ ћ2 а) 2 + 2m(E – U) = 0 ; б) d2 dx2 + 2m(E – U) = 0 ;  ћ2 d2 ⎝  2m⎛ – m2 2⎞  d2 2m  в) dx2 + ћ2 ⎜E x ⎟ = 0; г) 2 ⎠ dx2 + ћ2 E = 0 . Собственными значениями энергии уравнения бодно движущейся частицы, являются – ћ2  2m 2md2 dx2 = E для сво- 2ћ2 ⎛ 1⎞ meZ2e41  k2ћ2  а) Е =2ml2 n2; б) Е=⎜n+2⎟ ћ ; в) E =– 2ћ2 n2; г) Е = 2m .  ⎝ ⎠ ⎝ ⎠d2 2m   ⎝ ⎠ 2ћ2 ⎛ 1⎞ meZ2e41  k2ћ2  а) Е =2ml2 n2; б) Е=⎜n+2⎟ ћ ; в) E =– 2ћ2 n2; г) Е = 2m . Решение какого из приведенных ниже уравнений Шредингера приводит к собственным значениям энергии En= (n + ½)ћ? ⎝ ⎛ ћ2 2 ⎞ 2m  а) ⎜– 2m + U⎟ ⎠ = iћ t ; б) 2 + ћ2 (E – U) = 0 ; d2 ⎝  2m⎛ – m2 2⎞  d2 2m  в) dx2 + ћ2 ⎜E x ⎟ = 0; г) 2 ⎠ dx2 + ћ2 E = 0 . Какие из приведенных ниже графиков описывает волновую функцию час- тицы в потенциальной яме для возбужденного состояния?  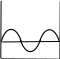  O l O l O l а) б) в) Какой из приведенных ниже графиков описывает распределение плотно- сти вероятности обнаружения частицы в потенциальной яме для основно- го состояния? 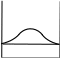 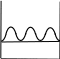 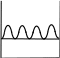 2 2 2 2 2 2O l O а) l O l б) в) Какой из приведенных ниже графиков описывает распределение плотно- сти вероятности обнаружения частицы в потенциальной яме для возбуж- денного состояния (n = 4)? 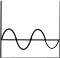 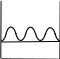 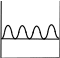 2 2 2 2O l O l O l а) б) в) Частица движется в одномерном потенциальном поле U(х), показанном на рисунке. Какое из приведенных ниже уравнений Шредингера соответст- вует случаю движения частицы с энергией E  U U0 U U0 ћ2 O l d2  а) dx2 + а) dx2 +2m(E – U ) = 0 ; б) d2 dx2 + 2mE = 0 ;  ћ2 0 – ћ2 d2 d2 2m  в) 2m dx2 + U0 = iћt ; г) dx2 + ћ2 (U0 – E) = 0 . Чему равна вероятность обнаружения частицы в середине потенциального ящика? Частица находится в возбужденном состоянии (n =2). а) w = 0,5; б) w = 0,195; в) w = 0. Частица с полной энергией Е0 движется в одномерном потенциальном поле U(х), изображенном на рисунке. Какой из приведенных ниже графи- ков правильно описывает характер изменения волновой функции (х)?  O l 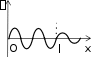 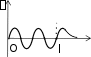 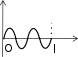 а) б) в) Частица с полной энергией Е>U 0 налетает на потенциальный барьер U(х), изображенный на рисунке. Уравнение Шредингера для данного случая за- пишется в виде: d2  dx2 + k2 dx2 + k2 = 0, где k2 = 2m(E – U ). ћ2 0 Общее решение уравнения имеет вид: 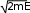 (x 0) = a exp(ik x) + bexp(–ikx), k= (x 0) = a exp(ik x) + bexp(–ikx), k=1 1 1 1 1 1 ћ . (x 0) = a exp(ik x) + bexp(–ikx), k = 2mE - U.  1 2 2 2 1 2 2 22 2 ћ Для рассматриваемого случая коэффициент отражения R определяется как 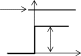 E U E UU0>0 O ⎛k1–k2⎞2 б) 2k1; в) k1– k2; г) 4k1k2. а) ⎜k + k ⎟ ; k1 + k2 k1 + k2 (k1 + k2)2 ⎝ 1 2⎠ Коэффициент прохождения Dпотенциального барьера, изображенного на рисунке, равен 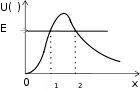 ⎛– 2 x2 ⎞  ⎜ ⎟ а) 0; б) 1; в) D0exp⎜ ⎝ ћ x1 2m(U – E) dx.⎟ ⎠ Частица с полной энергией Е налетает на потенциальный барьер U(х), изображенный на рисунке. Что произойдет с частицей? Какой из приве- денных ниже графиков правильно отражает распределение плотности ве- роятности 2(х) для рассматриваемого случая? 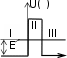 O 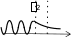 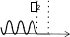 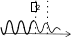 O O O O O Oа) б) в) а) частица отразится от потенциального барьера и не пройдет в области II и III. б) частица беспрепятственно пройдет над потенциальным барьером и попадет в область III; в) вероятность обнаружения частицы во всех областях отлична от нуля. |
