книга заданий пайтон. книга практических заданий, pyton. Сборник упражнений Введение в язык Python с задачами и решениями Бен Стивенсон Москва, 2021 удк 004. 438Python
 Скачать 2.24 Mb. Скачать 2.24 Mb.
|
5.3.3. Изменение порядка следования элементов в спискеБывает, что в списке содержатся нужные элементы, но расположены они не так, как требуется для решения той или иной задачи. Два элемента в списке можно поменять местами при помощи временной переменной и нескольких инструкций, как показано на примере ниже. # Создаем список data = [2.71, 3.14, 1.41, 1.62] # Меняем местами элементы в списке с индексами 1 и 3 temp = data[1] data[1] = data[3] data[3] = temp # Отображаем модифицированный список print(data) Изначально переменная списка data инициализируется значениями [2.71, 3.14, 1.41, 1.62]. После этого элемент списка с индексом 1, представляющий значение 3,14, присваивается временной переменной temp. Затем значение элемента с индексом 3 отправляется на место элемента с индексом 1, после чего операцию завершает присваивание значения из временной переменной элементу с индексом 3. На выходе мы получаем список с теми же элементами, но в измененном порядке: [2.71, 1.62, 1.41, 3.14]. Есть еще два способа изменить порядок следования элементов в списке, а именно воспользоваться специальными методами reverse и sort. Первый из них, как ясно из названия, меняет на противоположный порядок, в котором расположены элементы в списке, а второй сортирует элементы в порядке возрастания. Оба упомянутых метода могут быть вызваны применительно к спискам вовсе без аргументов. Вообще, список может быть отсортирован только в том случае, если его элементы могут сравниваться при помощи оператора <. Этот оператор в Python реализован для сравнения элементов самых разных типов, включая целые числа, числа с плавающей запятой, строки, списки и многие другие. В следующем примере мы попросим пользователя ввести перечень значений и сохраним их в список. После этого отсортируем список и выведем его на экран. # Создаем пустой список values = [] # Запрашиваем числа у пользователя и собираем список, пока он не оставит строку пустой line = input("Введите число (Enter для завершения): ") while line != "": num = float(line) values.append(num) line = input("Введите число (Enter для завершения: ") # Сортируем список по возрастанию values.sort() # Отображаем значения for v in values: print(v) 5.3.4. Поиск в спискеИногда бывает необходимо выяснить, содержится ли тот или иной элемент в заданном списке. В других ситуациях нам требуется получить индекс конкретного элемента в списке, который точно в нем присутствует. Оператор in и функция index в Python помогут нам справиться с этими задачами. Оператор in используется для определения факта вхождения элемента в список. Искомое значение при этом помещается слева от оператора, а список, в котором будет осуществляться поиск, – справа. Такое булево выражение возвращает True, если элемент входит в заданный список, и False в обратном случае. Метод index применяется для идентификации позиции искомого элемента в списке, значение которого передается в метод в качестве единственного аргумента. На выходе будет получен индекс первого вхождения элемента в список. Если искомого значения в списке не окажется, метод вернет ошибку. Так что программисты зачастую сначала определяют при помощи оператора in, есть ли элемент в списке, а уже затем прибегают к помощи метода index для поиска индекса интересующего элемента. В следующем фрагменте кода мы продемонстрируем сразу несколько методов и операторов, о которых говорили в этой главе. Начинается программа с запроса у пользователя целых чисел и добавления их в список. После этого пользователь должен ввести дополнительное целое число. Если в сформированном списке присутствует этот элемент, на экран будет выведен индекс его первого появления. В противном случае должно появиться сообщение о неудачном поиске. # Запрашиваем целые числа и собираем их в список, пока не будет введена пустая строка data = [] line = input("Введите целое число (Enter для окончания): ") while line != "": n = int(line) data.append(n) line = input("Введите целое число (Enter для окончания): ") # Запрашиваем у пользователя дополнительное число x = int(input("Введите дополнительное целое число: ")) # Отображаем индекс первого вхождения этого элемента в список (если он там есть) if x in data: print("Первое вхождение", x, "в списке – по индексу:", data.index(x)) else: print(x, "не находится в списке") 5.4. списки как возвращаемые значения и аргументыФункции могут возвращать списки. Как и значения других типов, списки из функций возвращаются при помощи ключевого слова return. После этого выполнение функции завершается, а управление передается следующей после вызова функции инструкции. Полученный таким образом список может быть сохранен в переменную или использован в расчетах. Списки также могут быть переданы в функции в качестве аргументов. Здесь тоже нет никаких отличий от значений других типов – имя списка передается в функцию в круглых скобках, как любой другой аргумент. Внутри списка переданный аргумент также сохраняется в переменной соответствующего параметра. Переменные параметров, представляющие собой списки, могут быть использованы в теле функции так же точно, как переменные любых других типов. Однако, в отличие от целых чисел, чисел с плавающей запятой, булевых выражений и строк, изменения, произведенные над элементами в списке внутри функции, могут повлиять на содержимое списка в вызывающем коде. В частности, изменения, сделанные в переданном списке посредством методов вроде append, pop или sort, окажут влияние на содержимое переданного в функцию аргумента и полученного на входе параметра. То же самое можно сказать и об изменении отдельных элементов спис ка путем присвоения им новых значений с указанием в квадратных скобках конкретных индексов. При этом присвоение нового значения всему списку в целом, когда слева от знака равенства находится только имя списка, влияет лишь на переменную параметра внутри функции, тогда как переменная, представляющая входной аргумент, остается неизменной. Различия в поведении списков в сравнении с переменными других типов применительно к их передаче функциям не случайны. Они обусловлены серьезными техническими доводами, выходящими за рамки данной книги. 5.5. упражненияВсе упражнения из данной главы должны быть решены при помощи списков. В программах, которые вы напишете, будут создаваться списки, модифицироваться, а также по ним будет выполняться поиск. Будут и задания, в которых переменные, хранящие списки, должны передаваться в функции в качестве аргументов или возвращаться из них. Упражнение 110. Порядок сортировки(Решено. 22 строки) Напишите программу, которая будет запрашивать у пользователя целочисленные значения и сохранять их в виде списка. Индикатором окончания ввода значений должен служить ноль. Затем программа должна вывести на экран все введенные пользователем числа (кроме нуля) в порядке возрастания – по одному значению в строке. Используйте для сортировки либо метод sort, либо функцию sorted. Упражнение 111. Обратный порядок(20 строк) Напишите программу, которая, как и в предыдущем случае, будет запрашивать у пользователя целые числа и сохранять их в виде списка. Индикатором окончания ввода значений также должен служить ноль. На этот раз необходимо вывести на экран введенные значения в порядке убывания. Упражнение 112. Удаляем выбросы(Решено. 44 строки) При анализе собранных по результатам научных экспериментов данных зачастую возникает необходимость избавиться от экстремальных значений, прежде чем продолжать двигаться дальше. Напишите функцию, создающую копию списка с исключенными из него n наибольшими и наименьшими значениями и возвращающую ее в качестве результата. Порядок следования элементов в измененном списке не обязательно должен в точности совпадать с источником. В основной программе должна быть продемонстрирована работа вашей функции. Для начала попросите пользователя ввести целые числа, затем соберите их в список и вызовите написанную вами ранее функцию. Выведите на экран измененную версию списка вместе с оригинальной. Если пользователь введет менее четырех чисел, должно быть отображено соответствующее сообщение об ошибке. Упражнение 113. Избавляемся от дубликатов(Решено. 21 строка) В данном упражнении вам предстоит разработать программу, в которой у пользователя будет запрошен список слов, пока он не оставит строку ввода пустой. После этого на экране должны быть показаны слова, введенные пользователем, но без повторов, – каждое по одному разу. При этом слова должны быть отображены в том же порядке, в каком их вводили с клавиатуры. Например, если пользователь на запрос программы введет следующий список слов: first second first third second программа должна вывести: first second third Упражнение 114. Отрицательные, положительные и нули(Решено. 36 строк) Напишите программу, запрашивающую у пользователя целые числа, пока он не оставит строку ввода пустой. После окончания ввода на экран должны быть выведены сначала все отрицательные числа, которые были вве- дены, затем нулевые и только после этого положительные. Внутри каждой группы числа должны отображаться в той последовательности, в которой были введены пользователем. Например, если он ввел следующие числа: 3, -4, 1, 0, -1, 0 и -2, вывод должен оказаться таким: -4, -1, -2, 0, 0, 3 и 1. Каждое значение должно отображаться на новой строке. Упражнение 115. Список собственных делителей(36 строк) Собственным делителем числа называется всякий его делитель, отличный от самого числа. Напишите функцию, которая будет возвращать список всех собственных делителей заданного числа. Само это число должно передаваться в функцию в виде единственного аргумента. Результатом функции будет перечень собственных делителей числа, собранных в список. Основная программа должна демонстрировать работу функции, запрашивая у пользователя число и выводя на экран список его собственных делителей. Программа должна запускаться только в том случае, если она не импортирована в виде модуля в другой файл. Упражнение 116. Совершенные числа(Решено. 35 строк) Целое число n называется совершенным, если сумма всех его собственных делителей равна самому числу n. Например, 28 – это совершенное число, поскольку его собственными делителями являются 1, 2, 4, 7 и 14, а 1 + 2 + 4 + 7 + 14 = 28. Напишите функцию для определения того, является ли заданное число совершенным. Функция будет принимать на вход единственный параметр и возвращать True, если он представляет собой совершенное число, и False – если нет. Разработайте небольшую программу, которая будет использовать функцию для идентификации и вывода на экран всех совершенных чисел в диапазоне от 1 до 10 000. При решении этой задачи импортируйте функцию, написанную в упражнении 115. Упражнение 117. Только слова(38 строк) В данном упражнении вы напишете программу, которая будет выделять слова из строки, введенной пользователем. Начните с создания функции, принимающей на вход единственный строковый параметр. В качестве результата она должна возвращать список слов из строки с удаленными знаками препинания, в число которых должны входить точки, запятые, восклицательный и вопросительный знаки, дефисы, апострофы, двоеточия и точки с запятыми. При этом не нужно избавляться от знаков препинания, стоящих внутри слова, таких как апостроф, служащий в английском языке для обозначения сокращений. Например, если на вход функции дать строку "Contractions include: don’t, isn’t, and wouldn’t.", функция должна вернуть следующий список: ["Contractions", "include", "don’t", "isn’t", "and", "wouldn’t"]. В основной программе, как обычно, должна происходить демонстрация вашей функции. Запросите у пользователя строку и выведите на экран все составляющие ее слова с удаленными знаками препинания. Вам понадобятся написанные при решении заданий 118 и 167 функции, так что убедитесь, что основная программа выполняется только в случае, если файл не импортирован в качестве модуля. Упражнение 118. Словесные палиндромы(34 строки) В упражнениях 75 и 76 мы уже имели дело со словами, являющимися палиндромами. Тогда мы анализировали буквы в слове с начала и конца, игнорируя пробелы и знаки препинания, чтобы понять, совпадает ли его написание в прямом и обратном направлениях. И хотя палиндромами обычно называют слова, это понятие вполне можно расширить. Например, английская фраза «Is it crazy how saying sentences backwards creates backwards sentences saying how crazy it is?» является словесным палиндромом, поскольку если читать ее по словам, игнорируя при этом знаки препинания и заглавные буквы, в обоих направлениях она будет звучать одинаково. Еще примеры английских словесных палиндромов: «Herb the sage eats sage, the herb» и «Information school graduate seeks graduate school information». Напишите программу, которая будет запрашивать строку у пользователя и оповещать его о том, является ли она словесным палиндромом. Не забывайте игнорировать знаки препинания при выявлении результата. Упражнение 119. Ниже и выше среднего(44 строки) Напишите программу, которая будет запрашивать у пользователя числа, пока он не пропустит ввод. Сначала на экран должно быть выведено среднее значение введенного ряда чисел, после этого друг за другом необходимо вывести список чисел ниже среднего, равных ему (если такие найдутся) и выше среднего. Каждый список должен предваряться соответствующим заголовком. Упражнение 120. Форматирование списка(Решено. 41 строка) Обычно при написании перечислений и списков мы разделяем их элементы запятыми, а перед последним ставим союз «и», как показано ниже: яблоки яблоки и апельсины яблоки, апельсины и бананы яблоки, апельсины, бананы и лимоны Напишите функцию, которая будет принимать на вход список из строк и возвращать собранную строку из его элементов в описанной выше манере. Хотя в представленном примере количество элементов списка ограничивается четырьмя, ваша функция должна уметь обрабатывать списки любой длины. В основной программе запросите у пользователя несколько элементов списка, отформатируйте их должным образом при помощи функции и выведите на экран. Упражнение 121. Случайные лотерейные номера(Решено. 28 строк) Для выигрыша главного приза необходимо, чтобы шесть номеров на лотерейном билете совпали с шестью числами, выпавшими случайным образом в диапазоне от 1 до 49 во время очередного тиража. Напишите программу, которая будет случайным образом подбирать шесть номеров для вашего билета. Убедитесь в том, что среди этих чисел не будет дубликатов. Выведите номера билетов на экран по возрастанию. Упражнение 122. «Поросячья латынь»(32 строки) «Поросячьей латынью» называют молодежный жаргонный язык, производный от английского. И хотя корни этого новообразованного языка неизвестны, упоминание о нем есть как минимум в двух документах, датированных XIX веком, а это значит, что ему уже больше сотни лет. Для перевода слова с английского на «поросячью латынь» нужно сделать следующее: если слово начинается с согласной буквы (включая y), то все буквы с начала слова и до первой гласной (за исключением y) переносятся в конец слова и дополняются сочетанием букв ay. Например, слово computer будет преобразовано в omputercay, а слово think – в inkthay; если слово начинается с гласной буквы (не включая y), к концу слова просто добавляется way. К примеру, слово algorithm превратится в algorithmway, а office – в officeway. Напишите программу, которая будет запрашивать у пользователя строку. После этого она должна переводить введенный текст на «поросячью латынь» и выводить его на экран. Вы можете сделать допуск о том, что все слова пользователь будет вводить в нижнем регистре и разделять их пробелами. Упражнение 123. «Поросячья латынь» (продолжение)(51 строка) Расширьте свое решение упражнения 122, чтобы ваш анализатор корректно обрабатывал символы в верхнем регистре и знаки препинания, такие как запятая, точка, а также восклицательный и вопросительный знаки. Если в оригинале слово начинается с заглавной буквы, то в переводе на «поросячью латынь» оно также должно начинаться с заглавной буквы, тогда как буквы, перенесенные в конец слов, должны стать строчными. Например, слово Computer должно быть преобразовано в Omputercay. Если в конце слова стоит знак препинания, он там же и должен остаться после выполнения перевода. То есть слово в конце предложения Science! необходимо трансформировать в Iencescay!. Упражнение 124. Линия наилучшего соответствия (41 строка) Линией наилучшего соответствия называется прямая, проходящая на наименьшем удалении от набора из n точек. В данном упражнении мы предположим, что каждая точка в коллекции обладает координатами x и y. Символы и мы будем использовать для подсчета средних значений по осям x и y соответственно. Линия наилучшего соответствия представлена формулой y = mx + b, где m и b вычисляются по следующим формулам: 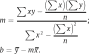 Напишите программу, которая будет запрашивать у пользователя координаты коллекции точек. При этом пользователь должен вводить сначала координату x, а затем y. Ввод координат может продолжаться до тех пор, пока пользователь не оставит пустым ввод координаты x. Отобразите формулу, характеризующую линию наилучшего соответствия, вида y = mx + b путем замены переменных m и b на значения, вычисленные по предыдущим формулам. Например, если пользователь введет три точки (1, 1), (2, 2.1) и (3, 2.9), итоговая формула должна приобрести вид y = 0,95x + 0,1. Упражнение 125. Тасуем колоду карт(Решено. 49 строк) Стандартная игральная колода состоит из 52 карт. Каждая карта соответствует одной из четырех мастей (пики, червы, бубны и трефы) и одному из 13 номиналов (от 2 до 10, валет (J), дама (Q), король (K) и туз (A)). Таким образом, каждая игральная карта может быть представлена при помощи двух символов. Первый из них указывает на номинал карты (от 2 до 9, T (десятка), J, Q, K или A), а второй – на масть (s = пики (spades), h = червы (hearts), d = бубны (diamonds) и c = трефы (clubs)). В табл. 5.1 представлены некоторые из возможных обозначений игральных карт. Таблица 5.1. Игральные карты
Начните с написания функции createDeck. В ней должны использоваться циклы для создания полной колоды карт путем сохранения в список двухсимвольных аббревиатур всех 52 карт. Именно этот список и будет возвращаемым из данной функции значением. На вход функция createDeck принимать параметры не будет. Напишите вторую функцию с именем shuffle, которая будет случайным образом перетасовывать карты в списке. Одна из техник тасования колоды заключается в проходе по элементам и перестановке их с любым другим случайным элементом в этом списке. Вы должны создать свой собственный цикл для тасования карт в колоде, а не пользоваться стандартной функцией shuffle языка Python. Используйте обе созданные функции в основной программе, в которой должна отображаться колода карт до и после тасования. Убедитесь, что основная программа выполняется только в случае, если файл не импортирован в качестве модуля. Примечание. Хороший алгоритм тасования игральной колоды должен быть беспристрастным, что означает равную вероятность расположения каждой из карт в колоде после тасования. Однако алгоритм, предложенный в этом упражнении и предполагающий обмен позициями между каждой из карт в колоде с любой другой случайной картой, не является таковым. В частности, карты, которые появляются позже в исходном списке, с большой вероятностью окажутся ближе к концу и в перетасованном списке. Как это ни странно, беспристрастной будет версия алгоритма, в которой при последовательном проходе по элементам каждый из них будет меняться позициями не со случайным элементом из всего списка, а со случайным элементом в диапазоне от позиции текущей карты и до конца колоды. Упражнение 126. Раздача карманных карт(44 строки) Во многих карточных играх после процедуры тасования колоды каждый игрок получает на руки определенное количество карт. Напишите функцию deal, принимающую на вход три параметра: количество игроков, количество раздаваемых каждому из них карт и саму колоду. Функция должна возвращать список рук, которые были розданы игрокам. При этом каждая рука, в свою очередь, тоже является списком из входящих в нее карт. Во время раздачи карт игрокам функция параллельно должна удалять розданные карты из переданной ей третьим параметром колоды. Также принято раздавать карты каждому игроку по одной строго по очереди. Придерживайтесь этих принципов и при написании своей функции. Воспользуйтесь своими наработками из упражнения 125 при построении структуры основной программы. Вам необходимо создать колоду карт, перетасовать ее и раздать четырем игрокам по пять карт. Выведите на экран карманные карты всех игроков, находящихся в раздаче, а также оставшиеся в колоде карты. Упражнение 127. Список уже отсортирован? (41 строка) Напишите функцию, показывающую, отсортирован ли переданный ей в качестве параметра список (по возрастанию или убыванию). Функция должна возвращать True, если список отсортирован, и False в противном случае. В основной программе запросите у пользователя последовательность чисел для списка, после чего выведите сообщение о том, является ли этот список отсортированным изначально. Примечание. Убедитесь в том, что вы правильно обрабатываете пустые списки, а также списки, состоящие из единственного элемента. Упражнение 128. Подсчитать элементы в списке(Решено. 48 строк) В стандартной библиотеке языка Python присутствует функция count, позволяющая подсчитать, сколько раз определенное значение встречается в списке. В данном упражнении вы создадите новую функцию countRange, которая будет подсчитывать количество элементов в списке, значения которых больше или равны заданному минимальному порогу и меньше максимального. Функция должна принимать три параметра: список, минимальную границу и максимальную границу. Возвращать она будет целочисленное значение, большее или равное нулю. В основной программе реализуйте демонстрацию вашей функции для нескольких списков с разными минимальными и максимальными границами. Удостоверьтесь, что программа будет корректно работать со списками, содержащими как целочисленные значения, так и числа с плавающей запятой. Упражнение 129. Разбиение строки на лексемы(Решено. 47 строк) Разбиение строки на лексемы (Tokenizing) представляет собой процесс преобразования исходной строки в список из подстрок, называемых лексемами (token). Зачастую со списком лексем работать бывает проще, чем со всей исходной строкой, поскольку в ней могут присутствовать неравномерные разрывы. Кроме того, иногда бывает непросто на лету определить, где заканчивается одна лексема и начинается другая. В математических выражениях лексемами являются, например, операторы, числа и скобки. Здесь и далее мы будем причислять к списку операторов следующие: *, /, ˆ, - и +. Операторы и скобки легко идентифицировать, поскольку эти лексемы всегда состоят ровно из одного символа и никогда не являются составной частью других лексем. Числа выделить бывает сложнее, поскольку эти лексемы могут состоять из нескольких символов. Любая непрерывная последовательность цифр должна восприниматься как одна числовая лексема. Напишите функцию, принимающую в качестве единственного входного параметра строку, содержащую математическое выражение, и преобразующую ее в список лексем. Каждая лексема должна быть либо оператором, либо числом, либо скобкой. Для простоты реализации в данном упражнении мы будем оперировать только целочисленными значениями. Функция должна возвращать созданный список лексем. При решении поставленной задачи вы можете принять допущение о том, что входная строка всегда будет содержать математическое выражение, состоящее из скобок, чисел и операторов. При этом в вашей функции должно быть предусмотрено, что лексемы могут отделяться друг от друга разным количеством пробелов, а могут и не отделяться вовсе. В основной программе продемонстрируйте работу функции, запросив у пользователя исходную строку и выведя на экран список составляющих ее лексем. Убедитесь, что основная программа выполняется только в случае, если файл не импортирован в качестве модуля. Упражнение 130. Унарные и бинарные операторы(Решено. 45 строк) Математические операторы бывают унарными (unary) и бинарными (binary). Унарные операторы взаимодействуют с одним значением, тогда как бинарные – с двумя. Например, в выражении 2 * –3 оператор * является бинарным, поскольку взаимодействует с двумя числами: 2 и -3. При этом сам оператор – здесь унарный, ведь он применяется только к одному числу 3. Одного лишь символа оператора недостаточно, чтобы определить, является ли он унарным или бинарным. Например, хотя в предыдущем случае оператор – был унарным, в выражении 2 – 3 он приобретет роль бинарного. Подобная неоднозначность, также характерная для оператора сложения, должна быть устранена до применения других операций к элементам списка лексем математического выражения. Напишите функцию для поиска унарных операторов + и – в списке лексем и их замены на сочетание символов u+ и u– соответственно. Функция должна принимать в качестве единственного параметра список лексем математического выражения и возвращать его копию с произведенной заменой унарных операторов. Оператор + или – можно идентифицировать как унарный в одном из двух случаев: если он идет первым в списке или если ему предшествует другой оператор либо открывающая скобка. Во всех остальных случаях оператор может считаться бинарным. В основной программе продемонстрируйте работу функции. Запросите у пользователя строку с математическим выражением, разбейте ее на лексемы, выделите в отдельный список унарные операторы и выведите их на экран. Упражнение 131. Инфиксная запись – в постфиксную(63 строки) Математические выражения часто записываются в инфиксной форме (infix form), когда оператор ставится между операндами, с которыми взаимодействует. И хотя такая форма записи наиболее распространена, существует и другая, именуемая постфиксной (postfix form), в которой оператор ставится после операндов. Например, инфиксной форме записи выражения 3 + 4 будет соответствовать постфиксный вариант 3 4 +. Чтобы преобразовать инфиксную форму записи в постфиксную, необходимо выполнить следующий алгоритм действий. Создаем новый пустой список operators Создаем новый пустой список postfix Для каждой лексемы в инфиксном выражении Если лексема представляет собой целое число, то Добавляем лексему к списку postfix Если лексема представляет собой оператор, то Пока список operators не пустой и последний элемент в operators не открывающая скобка и precedence(лексема) < precedence(последний элемент в operators), делаем Удаляем последний элемент из списка operators и добавляем его к postfix Добавляем лексему к списку operators Если лексема представляет собой открывающую скобку, то Добавляем лексему к списку operators Если лексема представляет собой закрывающую скобку, то Пока последний элемент в operators не является открывающей скобкой, делаем Удаляем последний элемент из списка operators и добавляем его к postfix Удаляем открывающую скобку из operators Пока список operators не пустой, делаем Удаляем последний элемент из списка operators и добавляем его к postfix Возвращаем postfix в качестве результата алгоритма Используйте свои наработки из упражнений 129 и 130 для разделения математических выражений на лексемы и поиска в них унарных операторов. После этого используйте алгоритм, приведенный выше, для преобразования выражения из инфиксной формы в постфиксную. Код, реализующий этот алгоритм, должен быть заключен в функцию, принимающую на вход список лексем инфиксного выражения (с помеченными унарными операторами). Возвращать функция будет список лексем в постфиксном выражении. В основной программе продемонстрируйте работу функции по преобразованию инфиксной формы записи математического выражения в постфиксную. Запросите у пользователя выражение инфиксного типа и выведите на экран его постфиксный аналог. Цель перевода математического выражения из одного вида в другой будет понятна вам, когда вы прочитаете текст упражнения 132. Кроме того, вам могут понадобиться наработки из заданий 96 и 97 при решении этого упражнения. И если первое решение вы можете использовать как есть, то решение задания 97 необходимо будет немного расширить, чтобы возвращался правильный приоритет для унарных операторов. Унарные операторы должны обладать более высоким приоритетом по сравнению с операциями умножения и деления, но более низким, если сравнивать с операцией возведения в степень. Упражнение 132. Выполнение постфиксных выражений(63 строки) Математические выражения, записанные в постфиксной форме, выполнять легче, чем те же выражения в инфиксной, поскольку в них нет скобок и не нужно учитывать старшинство операторов. Выражения в постфиксной форме могут быть выполнены при помощи реализации следующего алгоритма. Создаем новый пустой список values Для каждой лексемы в постфиксном выражении Если лексема представляет собой целое число, то Преобразуем лексему в целочисленный тип и добавляем к списку values Если лексема представляет собой унарный оператор –, то Удаляем последний элемент из списка values Применяем операцию логического НЕ к элементу и добавляем результат к списку values Если лексема представляет собой бинарный оператор, то Удаляем последний элемент из списка values и называем его right Удаляем последний элемент из списка values и называем его left Вычисляем результат применения оператора к операндам left и right Добавляем результат к списку values Возвращаем первый элемент списка values в качестве значения выражения Напишите программу, запрашивающую у пользователя математическое выражение в инфиксном виде, преобразующую его в постфиксную форму, выполняющую полученное выражение и выводящую на экран результат. Используйте при решении задачи свои наработки из упражнений 129, 130 и 131, а также алгоритм, приведенный выше. Примечание. В алгоритмах, предложенных для решения упражнений 131 и 132, не предусмотрена обработка возможных ошибок. В результате ваши программы могут выдавать ошибки или выполняться неправильно, если пользователь введет что-то неожиданное. Эти алгоритмы могут быть расширены и дополнены по желанию во избежание возникновения ошибок. Сами ошибки можно корректно обрабатывать и выводить соответствующие сообщения на экран. Если вам интересно попробовать это сделать, никто вас останавливать не будет. Упражнение 133. Содержит ли список подмножество элементов? (44 строки) Подмножеством элементов, или подсписком (sublist), мы будем называть список, являющийся составной частью большего списка. Подсписок может содержать один элемент, множество элементов, а также быть пустым. Например, [1], [2], [3] и [4] являются подсписками списка [1, 2, 3, 4]. Список [2, 3] также входит в состав [1, 2, 3, 4], но при этом список [2, 4] не является подсписком [1, 2, 3, 4], поскольку в исходном списке числа 2 и 4 не соседствуют друг с другом. Пустой список может быть рассмотрен как подсписок для любого списка. Таким образом, список [] является подсписком [1, 2, 3, 4]. Также список является подсписком самого себя, то есть [1, 2, 3, 4] – это подсписок для [1, 2, 3, 4]. В рамках данного упражнения вам необходимо написать функцию isSublist, определяющую, является ли один список подсписком другого. На вход функции должны поступать два списка – larger и smaller. Функция должна возвращать значение True только в том случае, если список smaller является подсписком списка larger. Напишите также основную программу для демонстрации работы функции. Упражнение 134. Все подсписки заданного списка(Решено. 41 строка) Используя определение подсписка из упражнения 133, напишите функцию, возвращающую список, содержащий все возможные подсписки заданного. Например, в число подсписков списка [1, 2, 3] входят следующие: [], [1], [2], [3], [1, 2], [2, 3] и [1, 2, 3]. Заметьте, что ваша функция должна вернуть как минимум один пустой список, гарантированно являющийся подсписком для любого списка. Напишите основную программу, демонстрирующую работу функции применительно к нескольким исходным спискам. Упражнение 135. Решето Эратосфена(Решено. 33 строки) Решето Эратосфена – алгоритм, изобретенный более 2000 лет назад и служащий для нахождения всех простых чисел от 2 до некоторого целого числа n. Описание этого алгоритма приведено ниже. Выписываем все целые числа от 0 до заданной границы Вычеркиваем 0 и 1 как непростые числа Устанавливаем значение переменной p, равное 2 Пока p меньше указанного числа, делать Вычеркиваем все числа, кратные p, но не его само Устанавливаем значение p, равное следующему невычеркнутому числу Выводим все числа, оставшиеся незачеркнутыми Ценность данного алгоритма заключается в том, что на бумаге очень легко вычеркнуть все числа, кратные определенному. Для компьютера это также не самая сложная задача – с этим может прекрасно справиться инструкция for с третьим параметром, переданным функции range. Мы знаем, что вычеркнутые числа на листочке не являются простыми, но физически они никуда с листа не деваются и должны участвовать в дальнейшем алгоритме. Так что и в компьютерной симуляции не стоит «вычеркивать» элемент путем его удаления из списка – вместо этого лучше будет присвоить ему значение 0. После завершения алгоритма все ненулевые числа в списке и будут простыми. Напишите программу на Python, реализующую указанный выше алгоритм для отображения простых чисел в интервале от двух до значения, введенного пользователем. Если алгоритм будет реализован правильно, ваша программа справится с выводом всех простых чисел от двух до миллиона всего за пару секунд. Примечание. Приведенный в данном упражнении алгоритм поиска простых чисел, названный в честь Эратосфена, был далеко не единственным вкладом греческого математика в науку. Ему также приписывают вычисление длины окружности Земли и градус наклона ее оси. Кроме того, с 235 г. до н. э. он служил хранителем знаменитой Александрийской библиотеки.  |
