Калиничев В.Н., Безбах Т.В. 
Сборник задач и контрольных заданий по
инженерно-геологической графике
Москва
2009
ПРОЕКЦИИ С ЧИСЛОВЫМИ ОТМЕТКАМИ
Точка
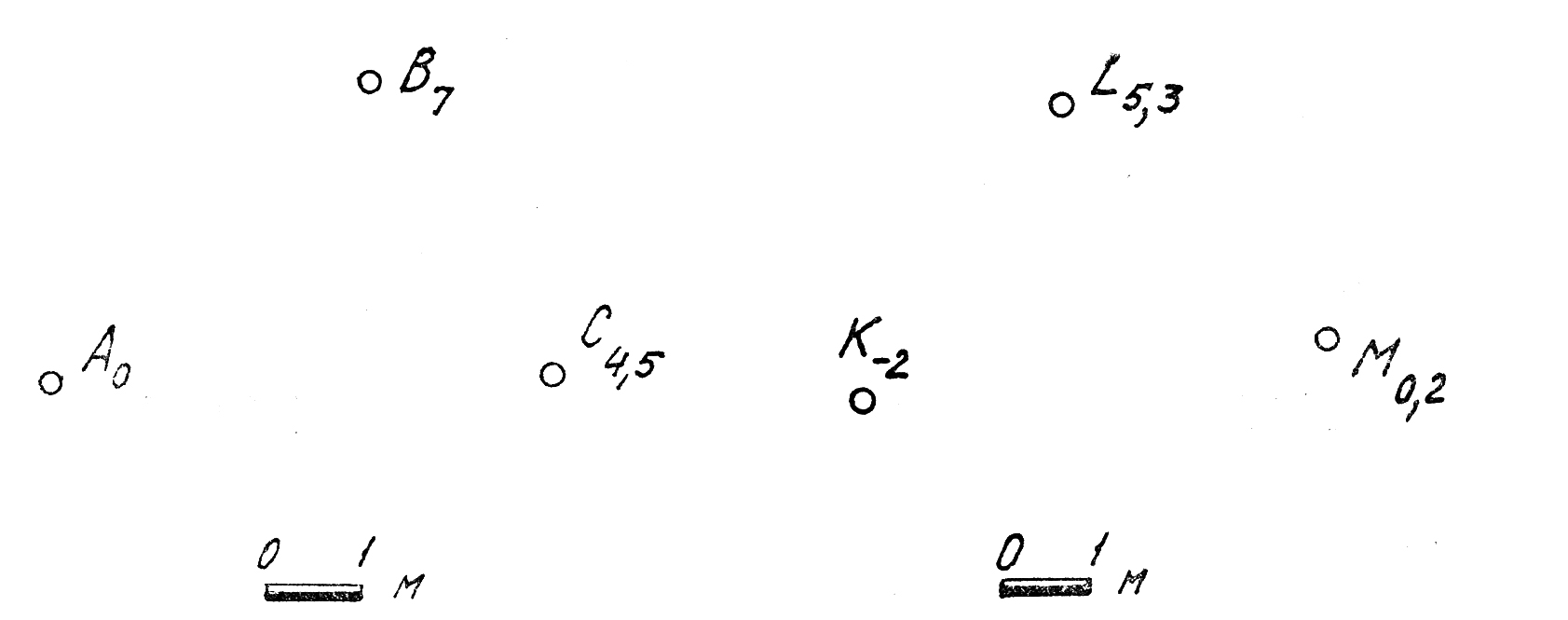
1. Определить отметки точек K, L и M, если плоскость проекций П0 будет смещена вниз на расстояние 2м.
Прямая линия
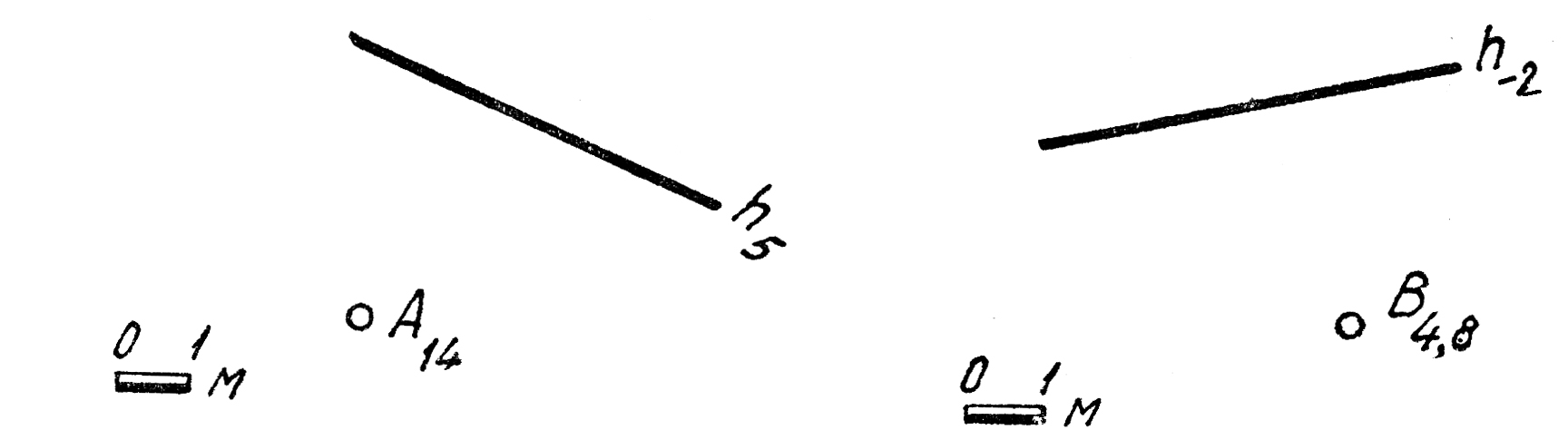
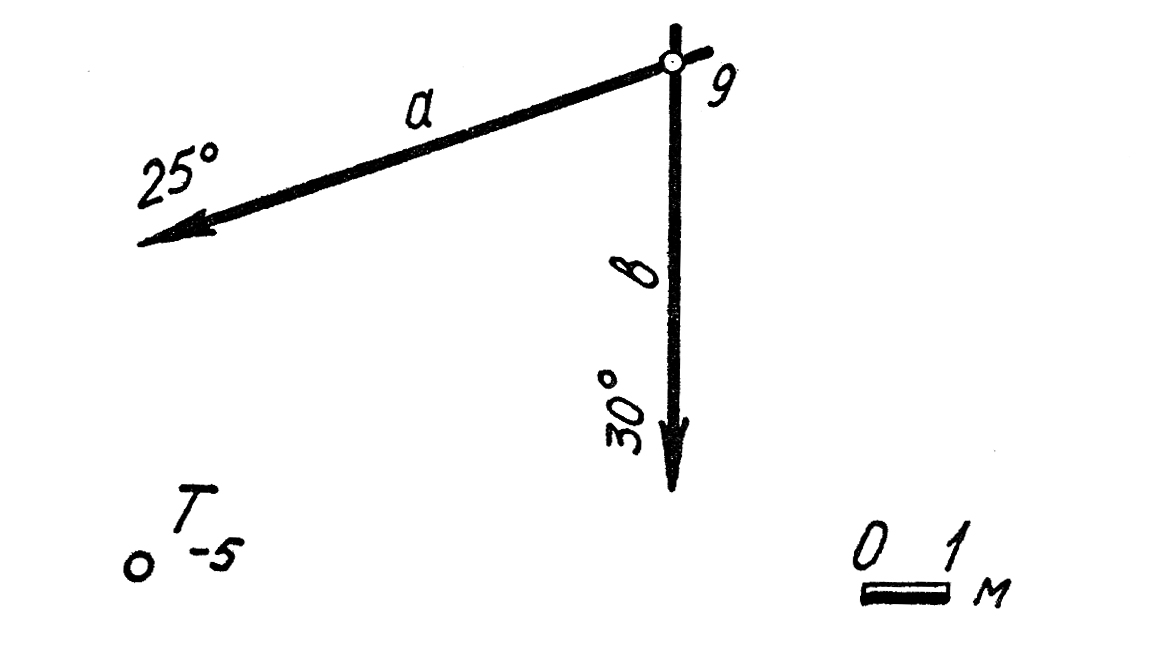
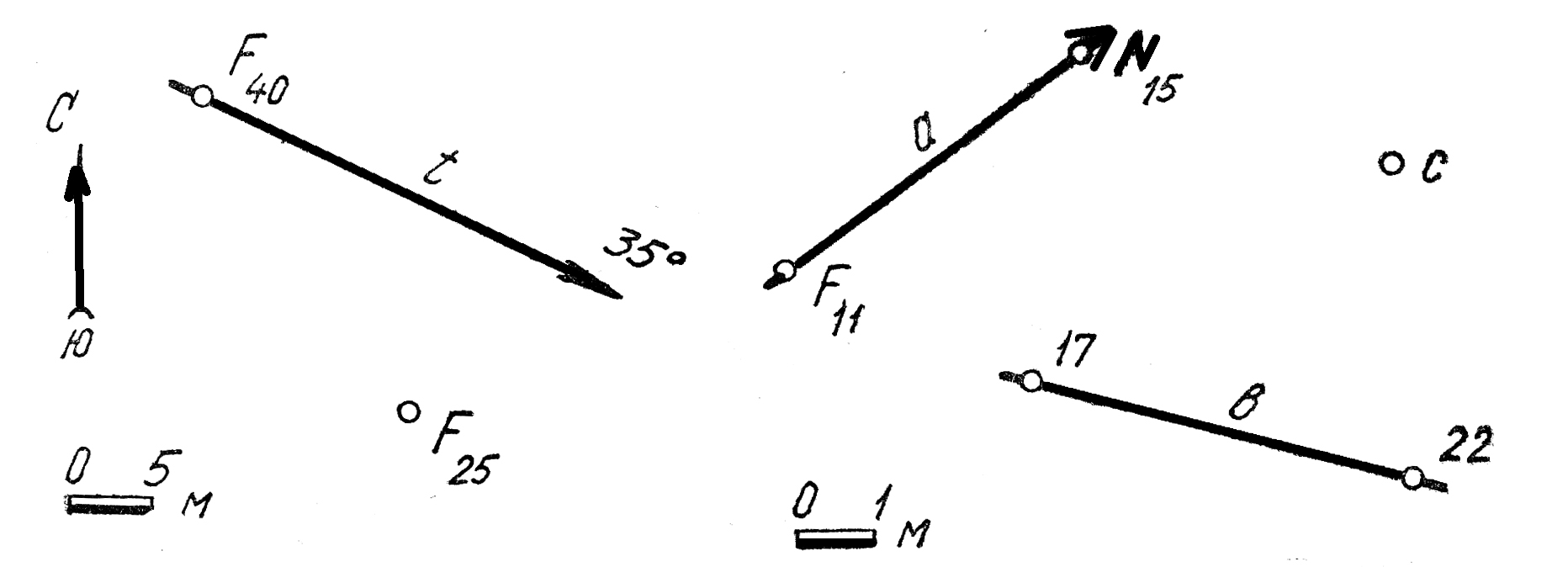
2. Определить азимуты падения прямых m(А5В1), n(C10D5), t(Es300).
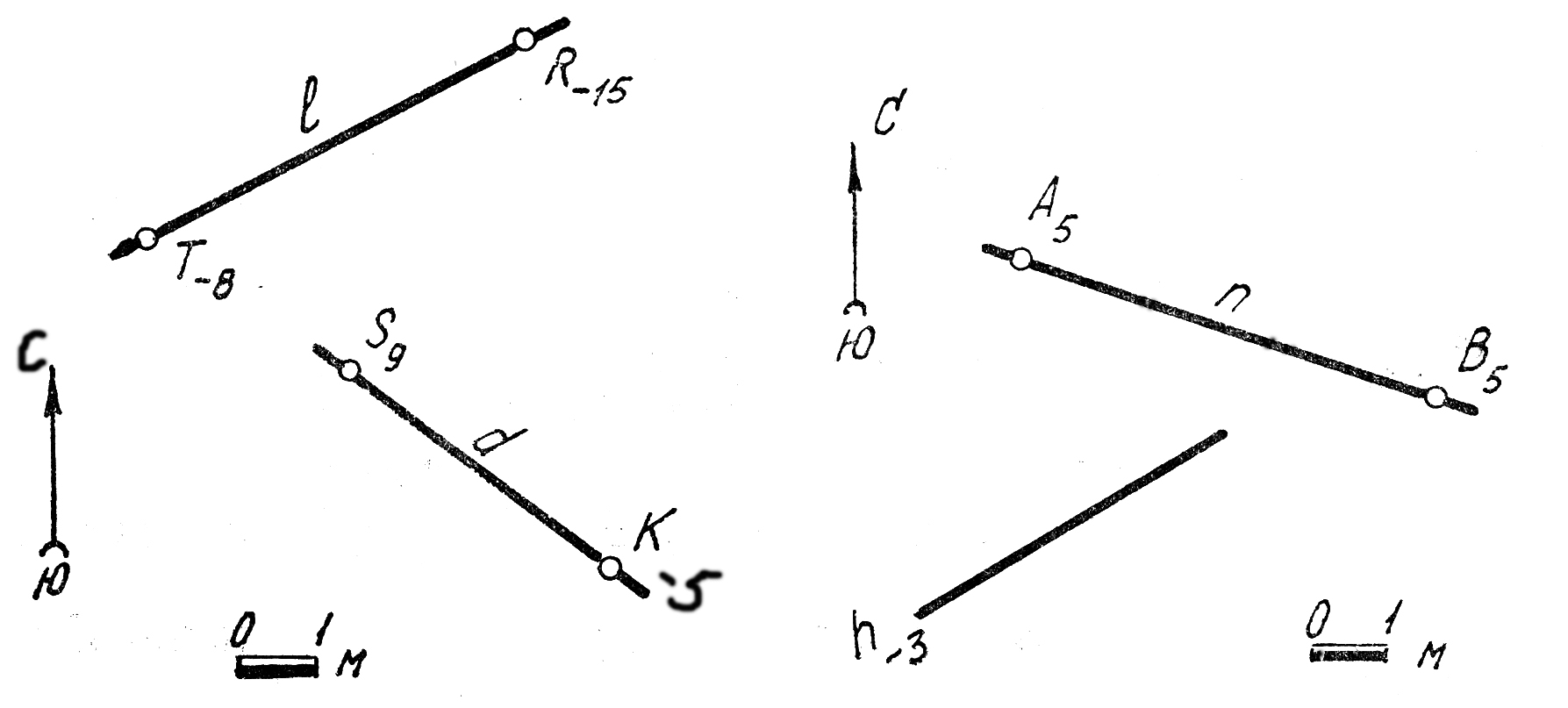
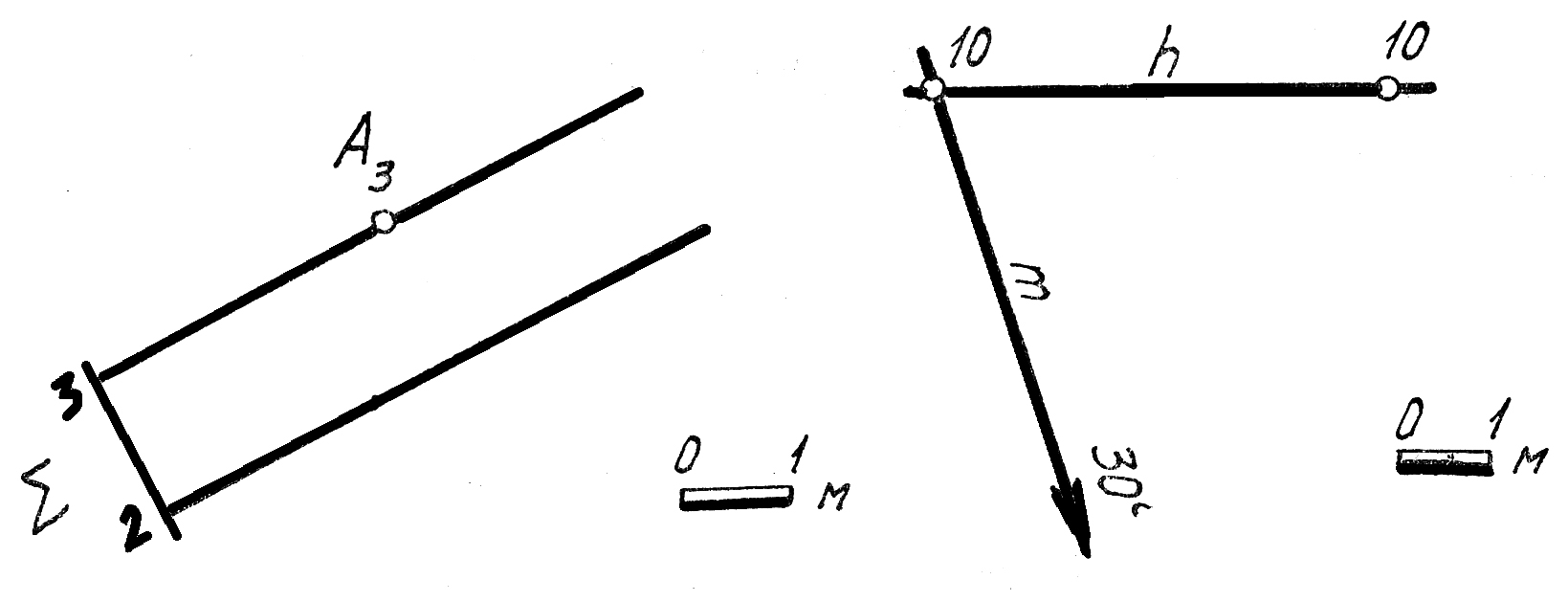
3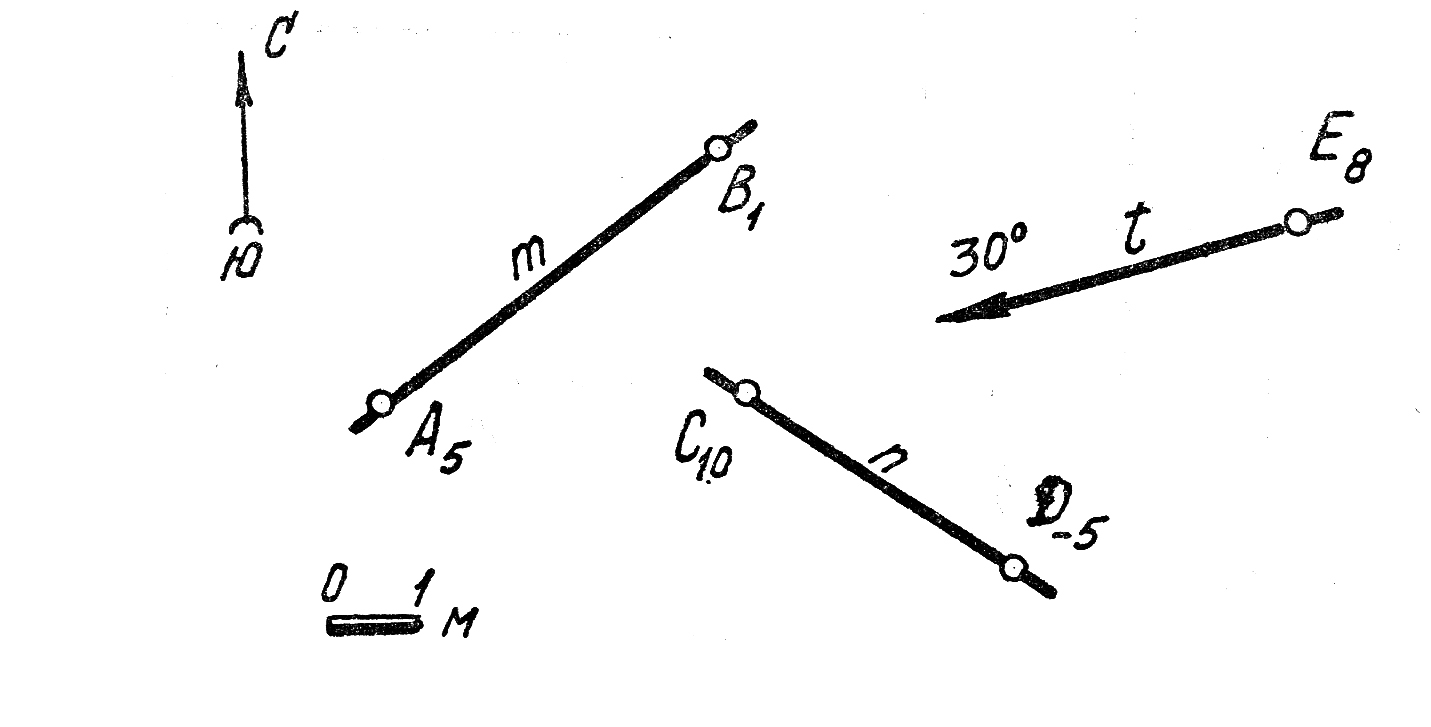 . Определите азимуты простирания горизонтальных прямых n(A5B5) и h-3
Через точку Впровести прямую t, азимут которой был бы равен 203°, а угол падения 230.
5. Через точку С провести горизонтальную прямую, азимут простирания которой был бы равен 127°.
6. Через точку Dпровести горизонтальную прямую, азимут простирания которой был бы равен 83°.
 
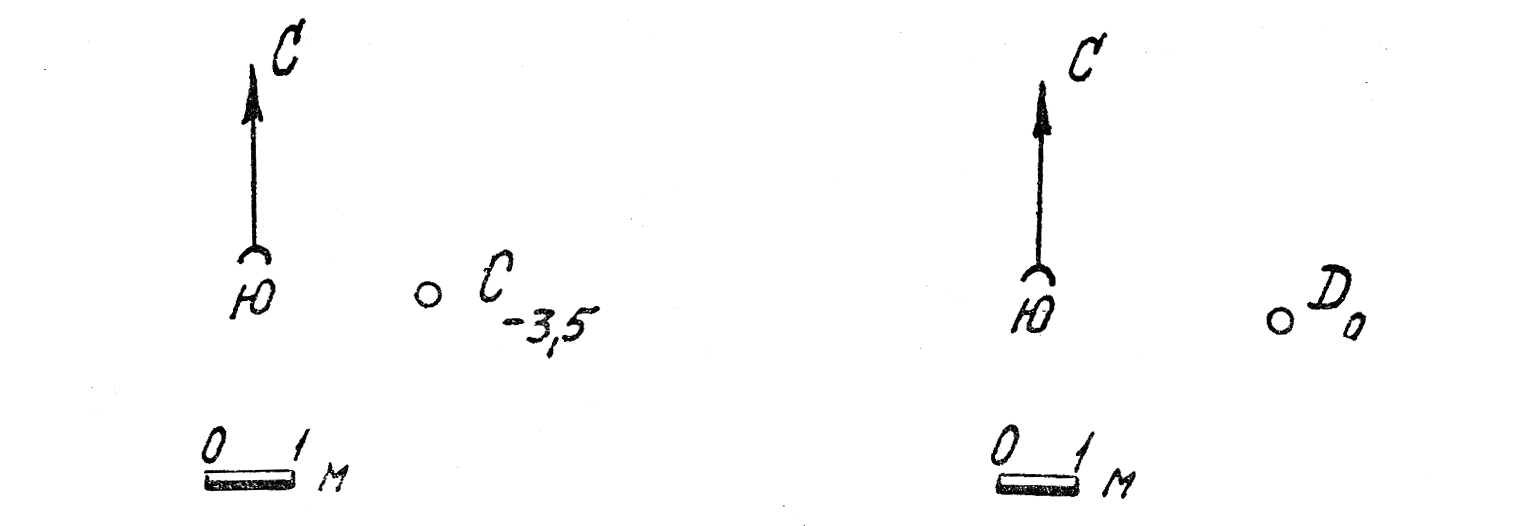
7. Определить истинную длину отрезка CD (C8,5D-4,25). Найти на прямой точку F с числовой отметкой 5.
8. На прямой пнайти точку D, удаленную от точки Fна расстояние 8,75 м.
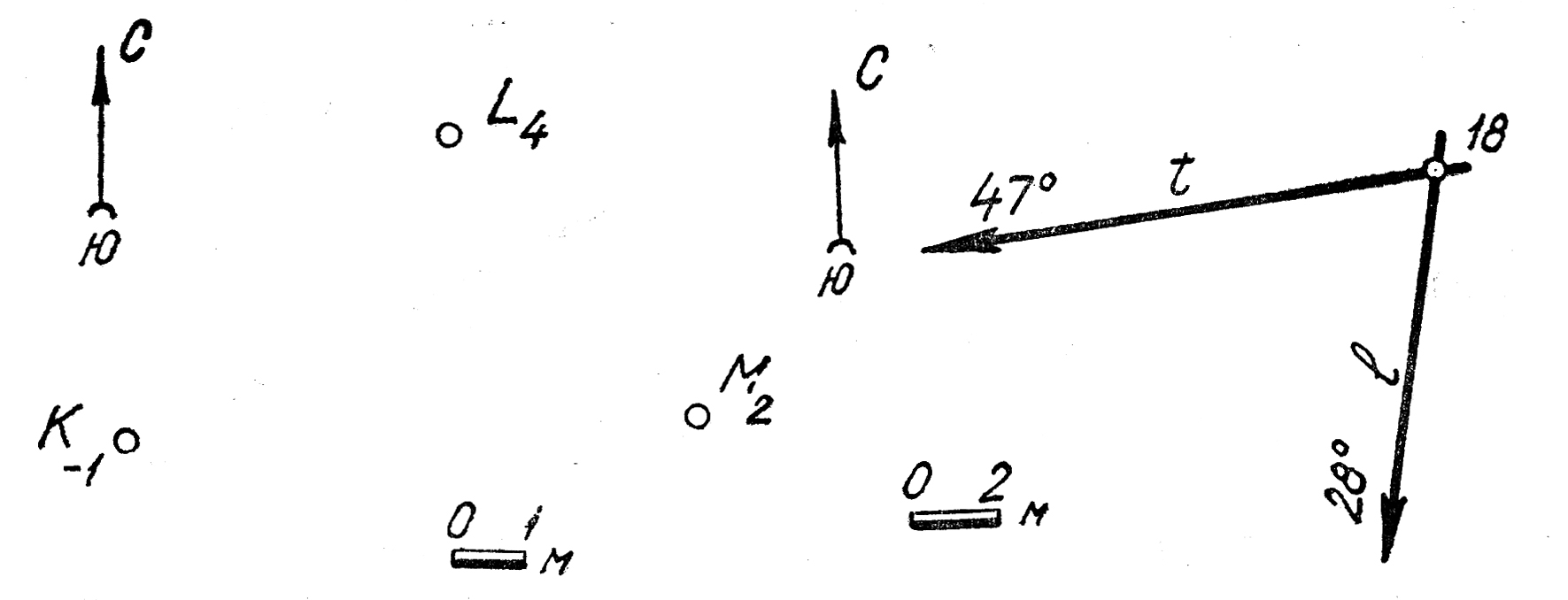
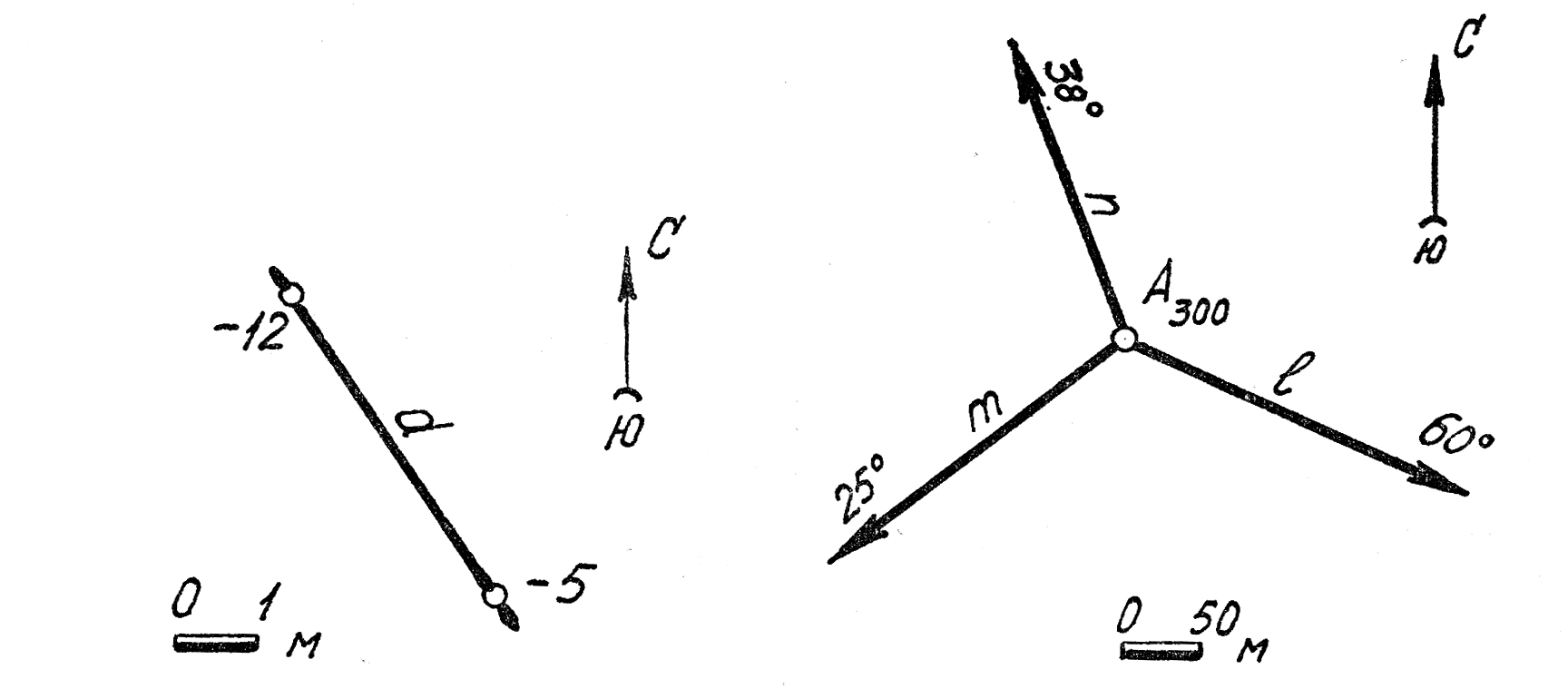
9. Определить элементы залегания прямой l(M8N0).
  
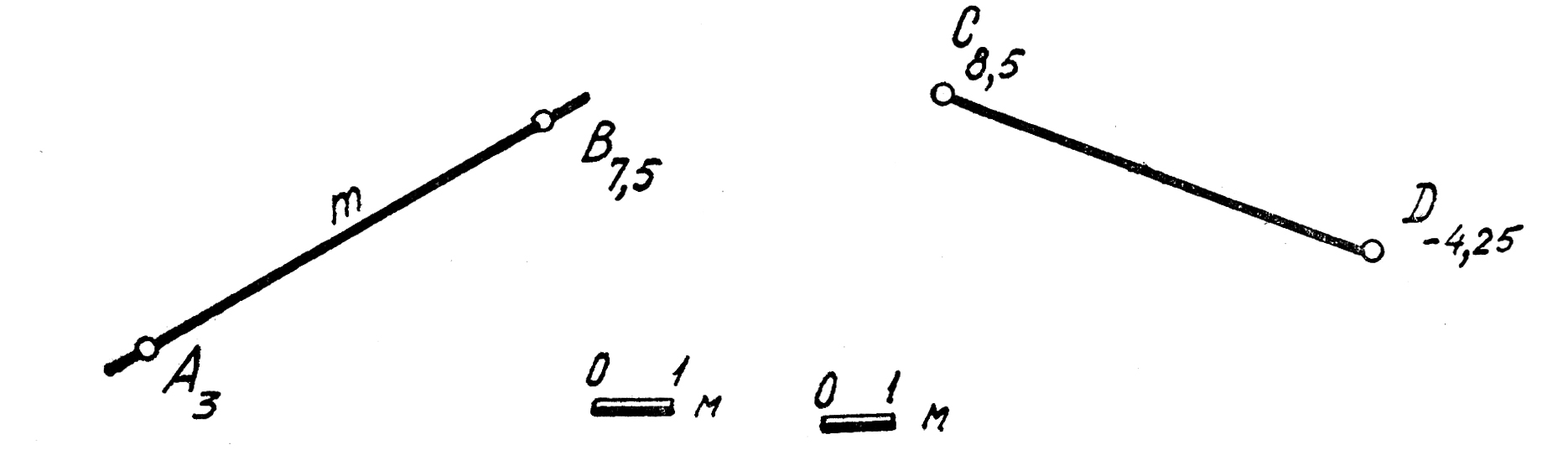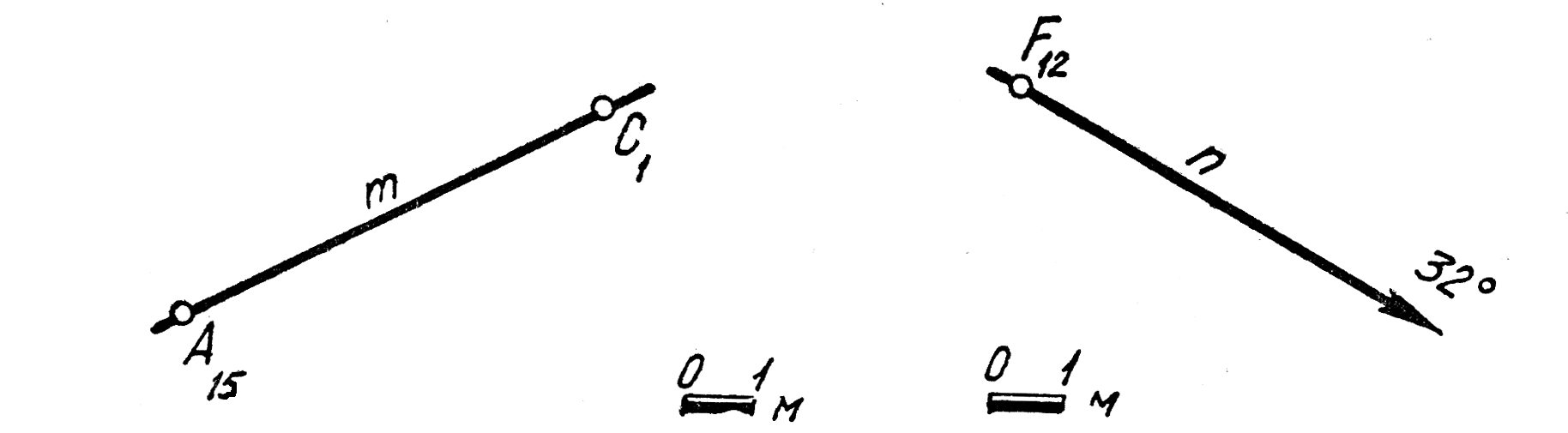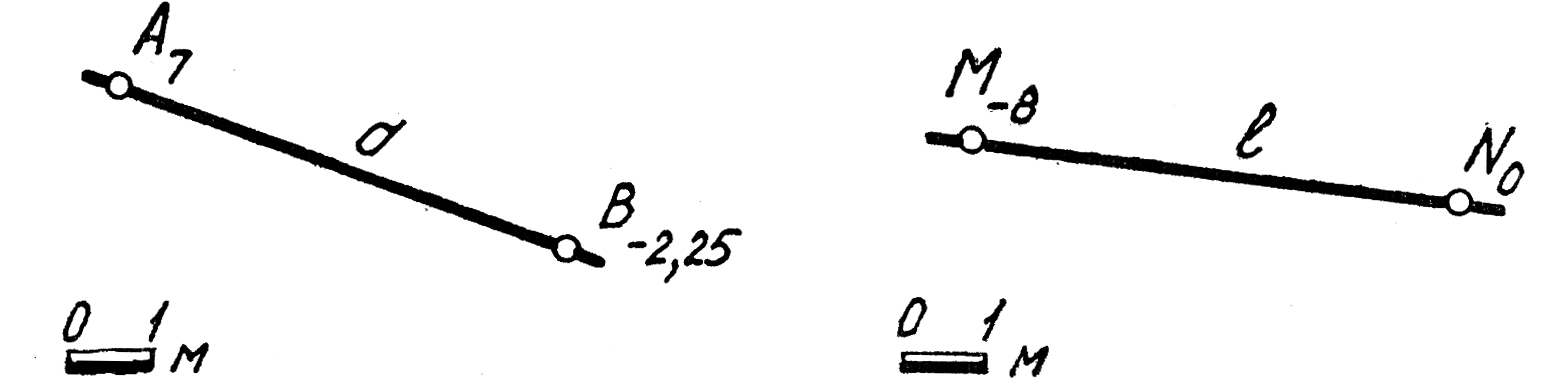
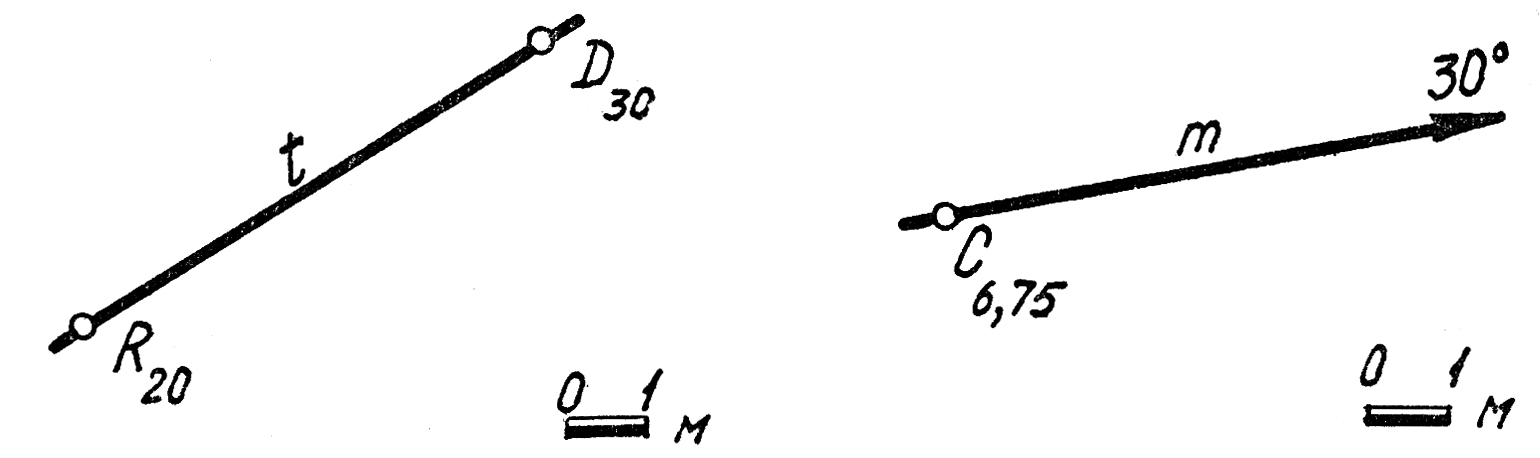
10. Построить проекцию точки R, принадлежащей прямой m (C6,7530°), отметка которой была бы равна 3,5 м. Решить задачу с помощью построения профиля и масштаба заложений.
11. Определить истинное расстояние от точки Вдо прямой h
12.Через точку Rпровести произвольную прямую, которая скрещивалась бы с прямой тпод углом 90°. Определить истинное расстояние между конкурирующими точками прямых.
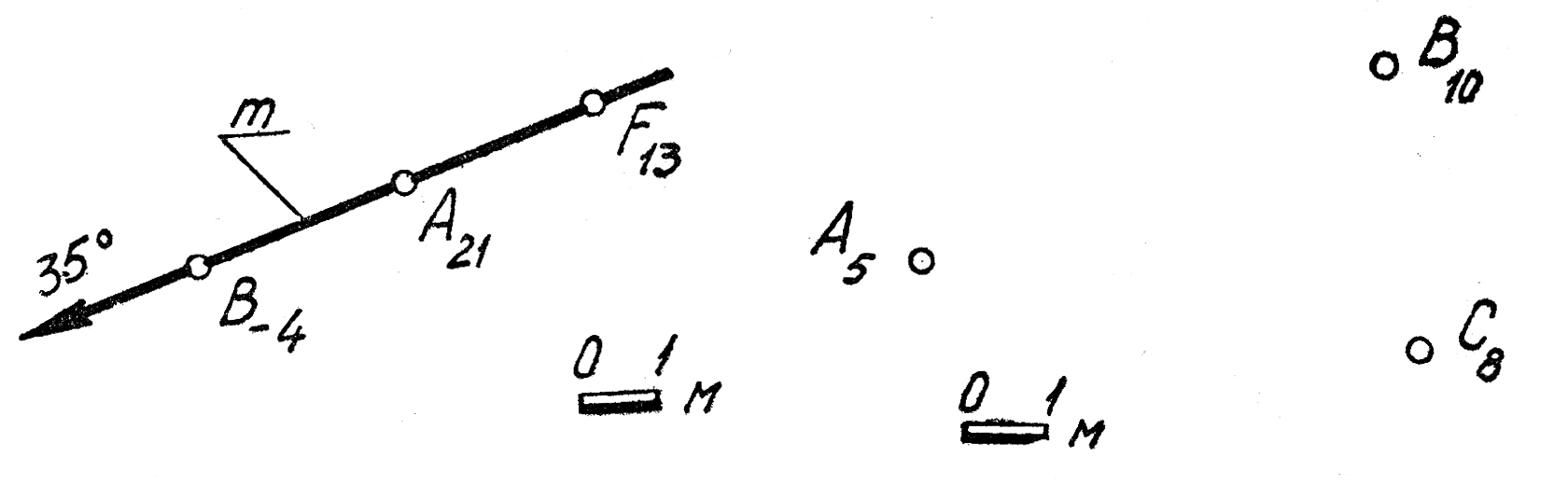 13. Определить истинное расстояние от точек В и А до прямой m(F13350).
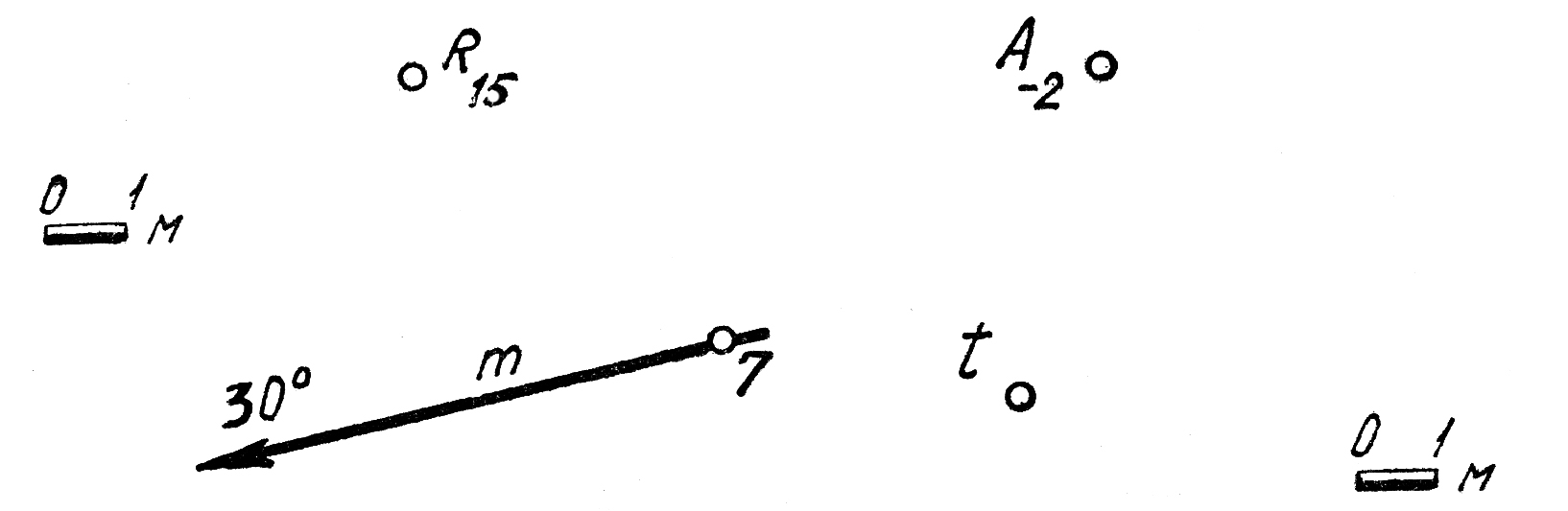
Плоскость
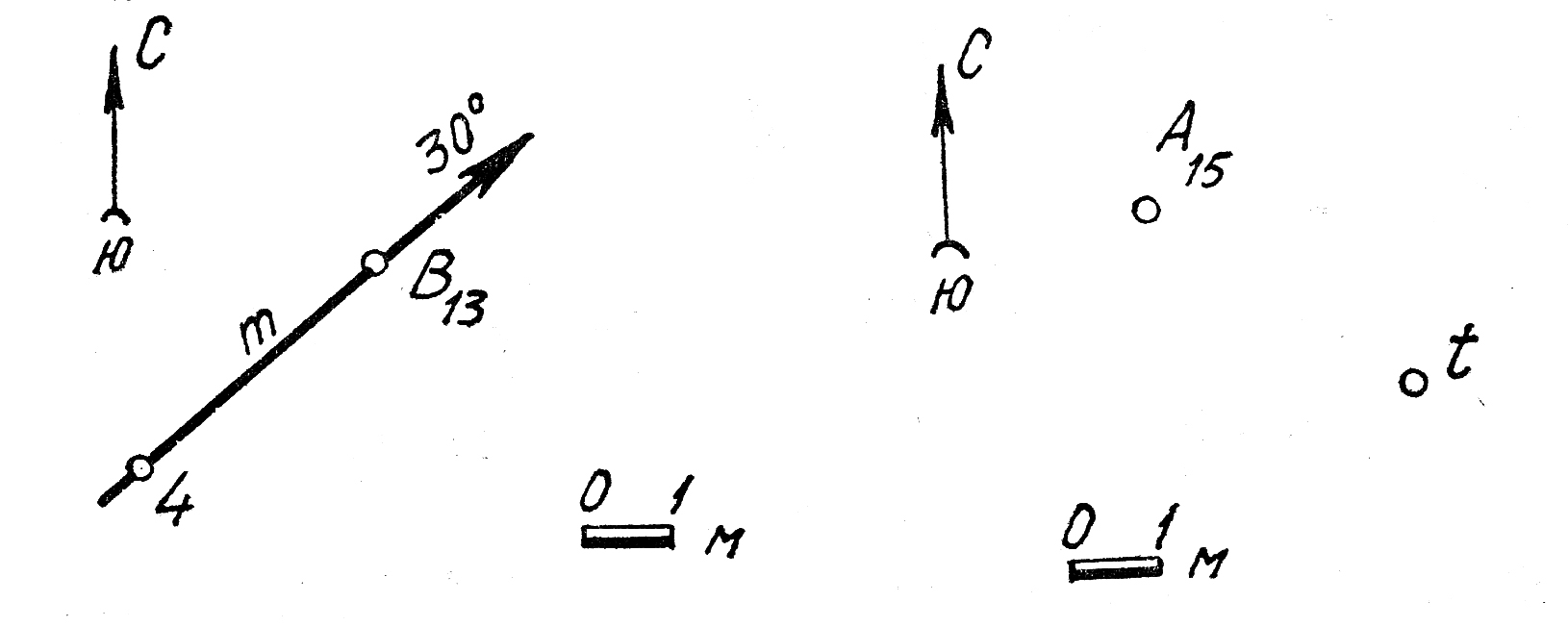
Определить элементы залегания плоскости Ω(t×l).
15. Определить элементы залегания плоскости Т(В13 т)
 
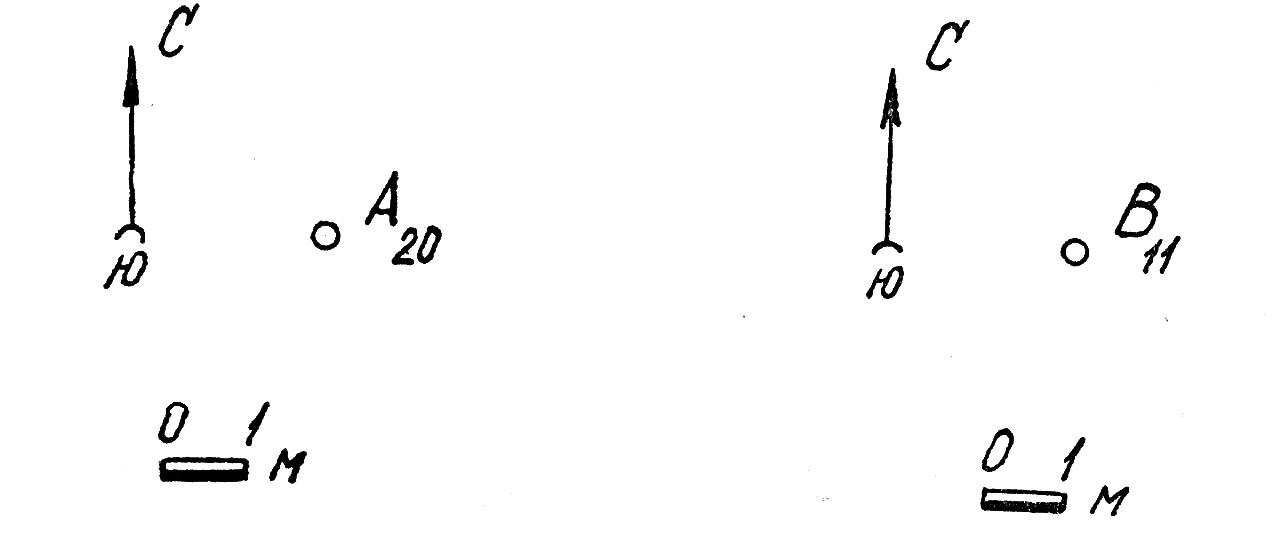
16.Изобразить плоскость Σ(В11 аз. пад. 245° 30°) горизонталями; высота сечения 1 м.
17. Через прямую ппровести плоскость Λ, угол падения которой был бы равен 62°. Определить азимут линии падения плоскости.
 
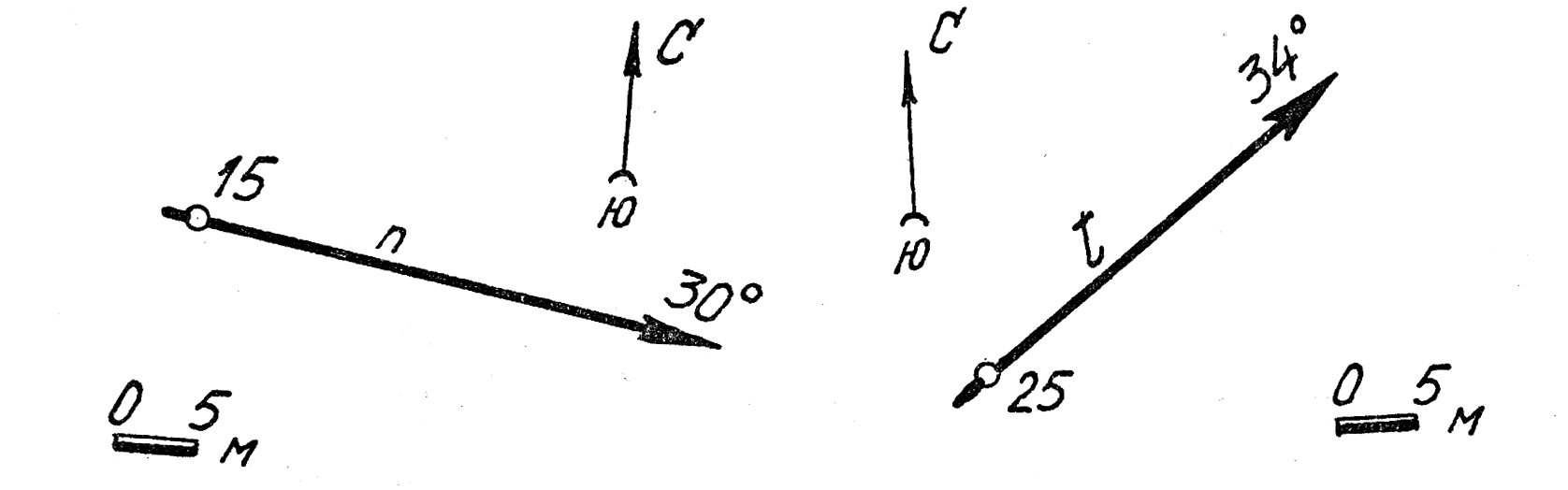
18. Определить элементы залегания плоскости Σ исходя из условия, что наклонные прямые т, пи l, проходящие через точку А, пересекают эту плоскость в точках В, Си Dна горизонтах 100, 150 и 70 м.
Взаимное расположение двух плоскостей
19. Через точку Спровести плоскость Ф, которая была бы параллельна плоскости v(а×b).
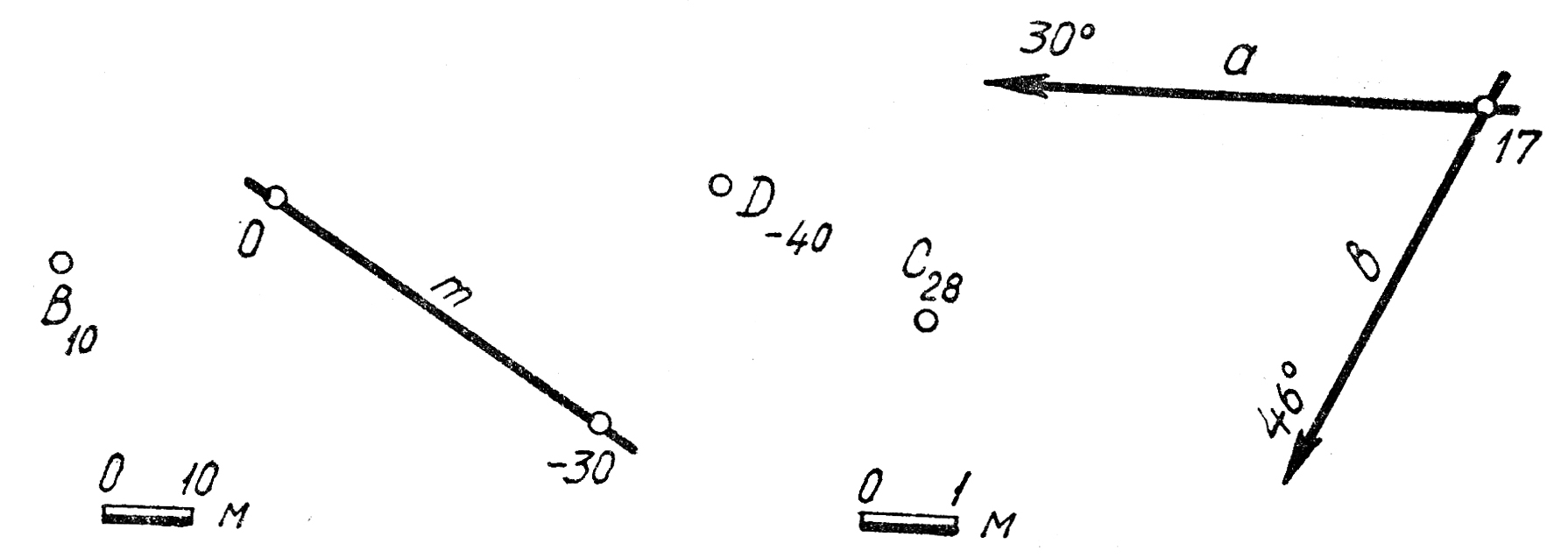
Через точку Впровести плоскость ∑, которая была бы параллельна плоскости Ф(A10 m).
21. Построить линию т пересечения плоскости Σ с плоскостью Λ.
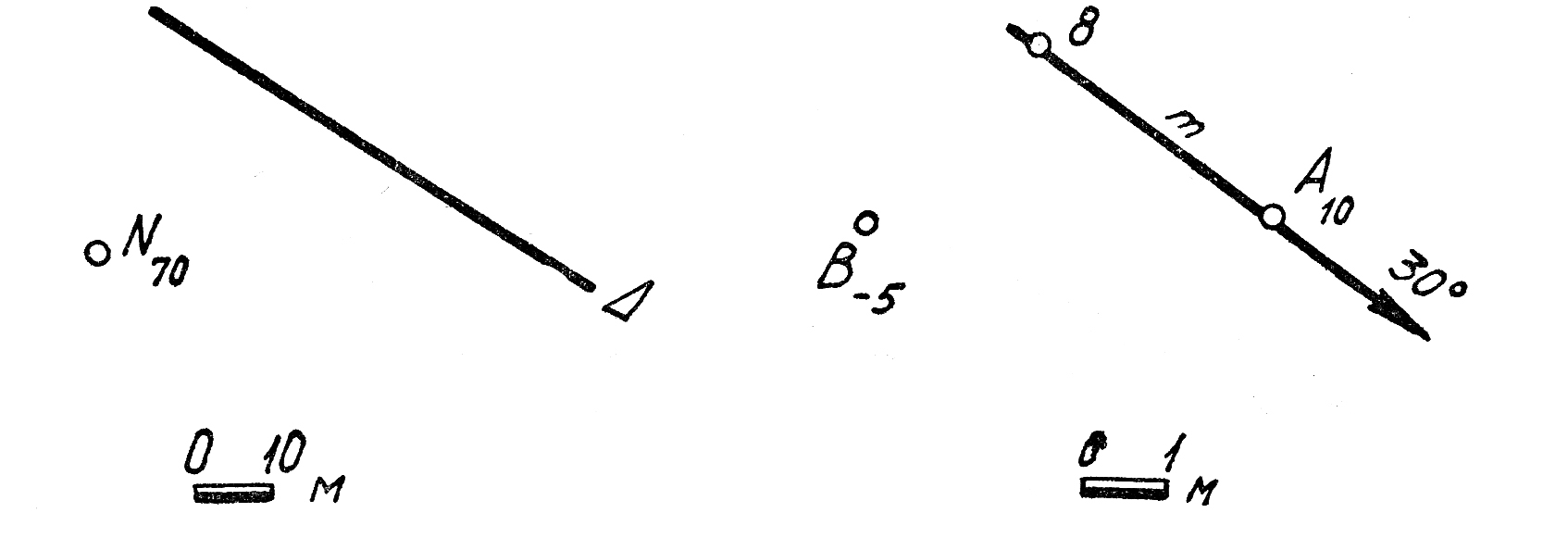
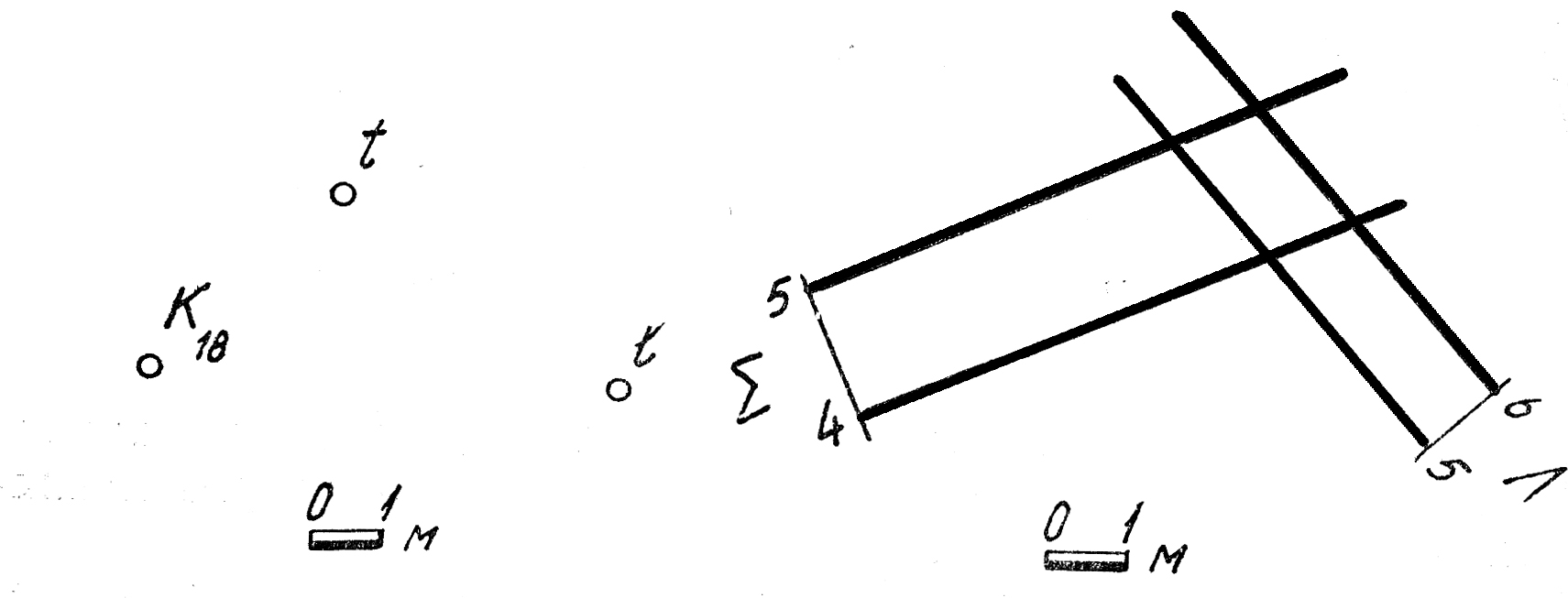
22. Построить линию b пересечения плоскости Т с плоскостью Р.
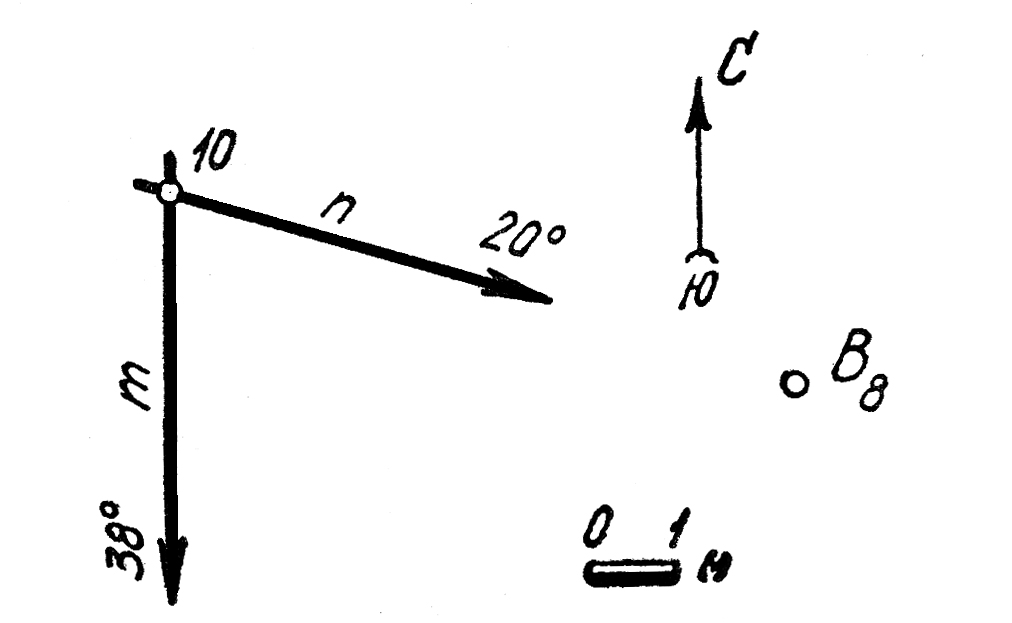  23. Построить линию а пересечения плоскости Θ(т×п)с плоскостью
Δ(В8аз. простир. l50° 90°).
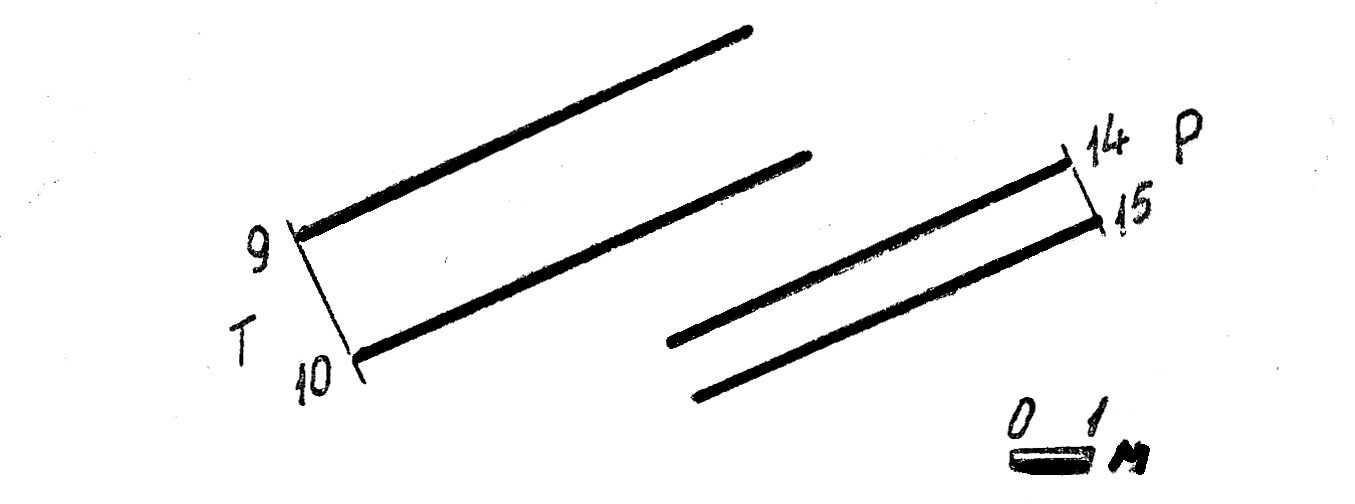
24. Построить линию tпересечения плоскости Ω с плоскостью Σ, проходящей через прямую m(А12300)перпендикулярно к плоскости Σ.
25. Определить истинное расстояние между параллельными плоскостями Т(m×n) и Ω(t×l).
 
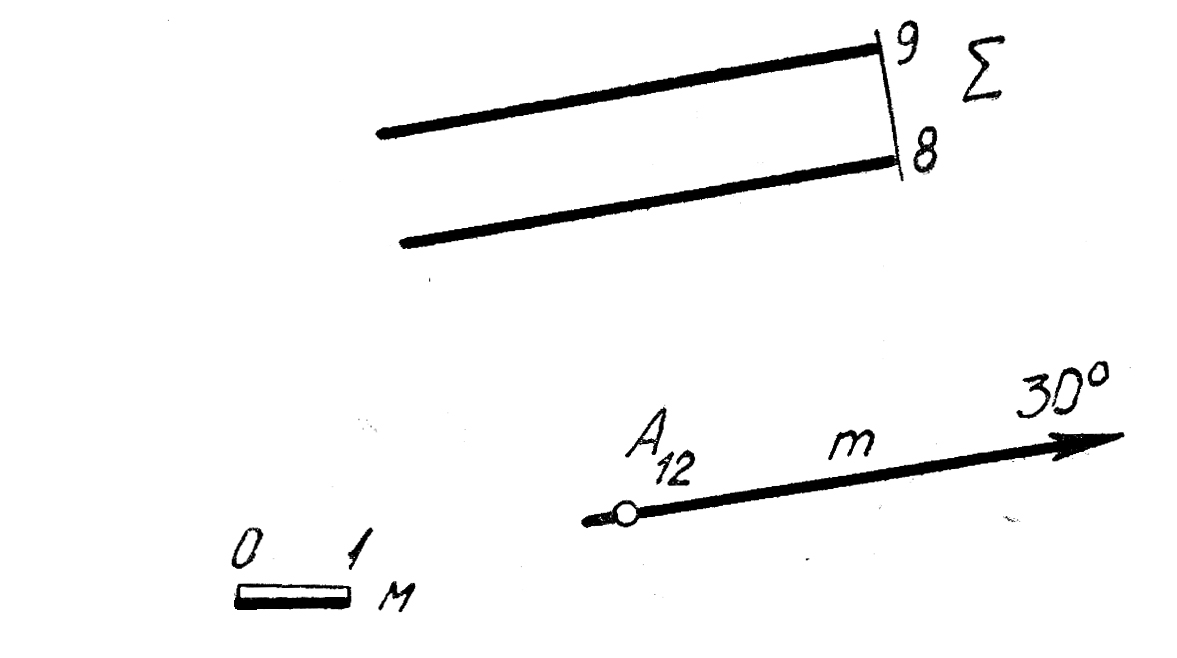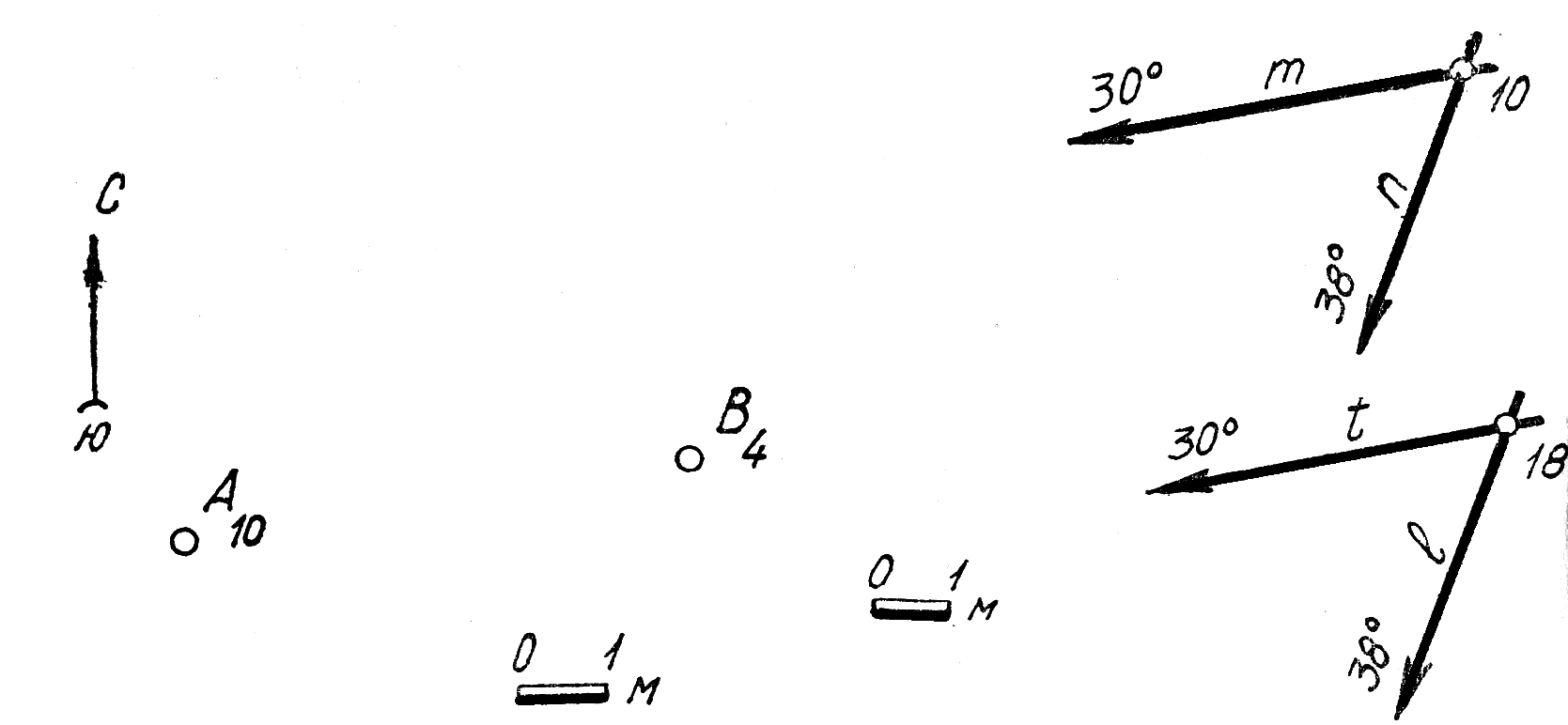
26. Через точку Апровести прямую b, которая пересекла бы скрещивающиеся прямые ти п.
Взаимное расположение прямой и плоскости
27. В каком направлении надо пересечь плоскость Ψ(m×h) вертикальной плоскостью Θ, чтобы в сечении получить прямую t, угол падения которой был бы равен 15°.
28. Через точку Тпровести прямую l, которая была бы параллельна плоскости Ω(a×b)и имела бы угол падения, равный 15°
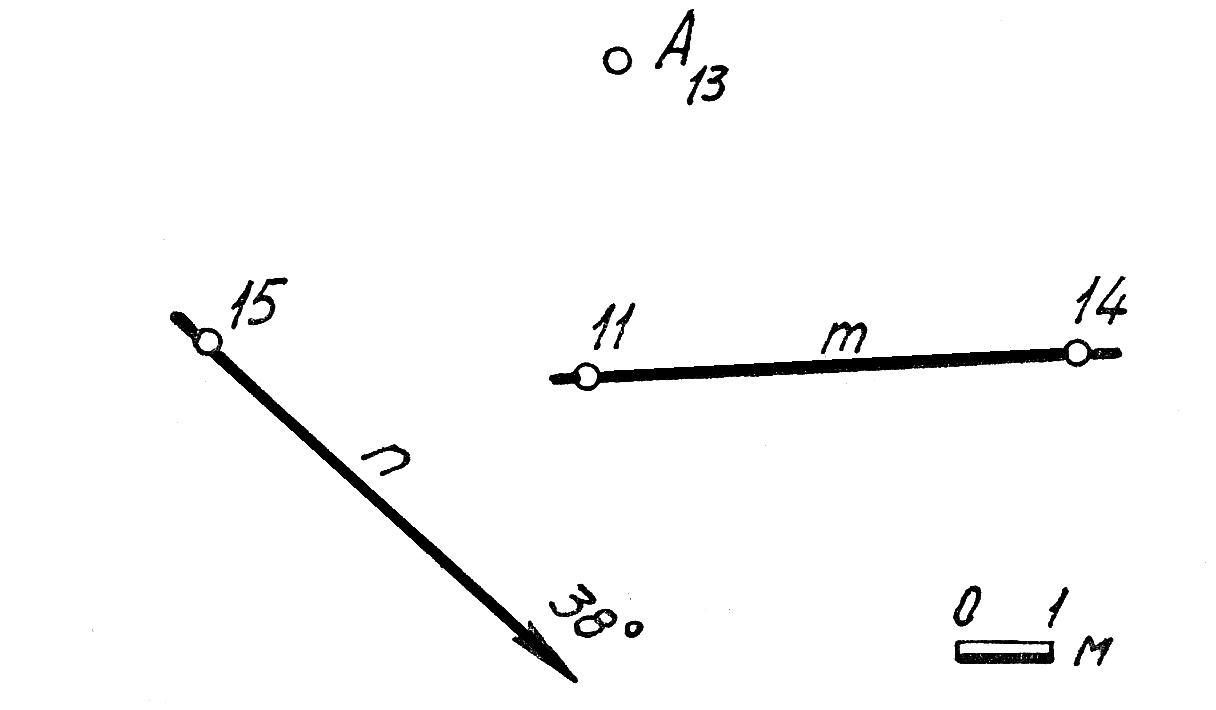
29. Через точку Fпровести плоскость Δ, которая была бы параллельна прямой t(R17, 250) и имела бы угол падения равный 57°.
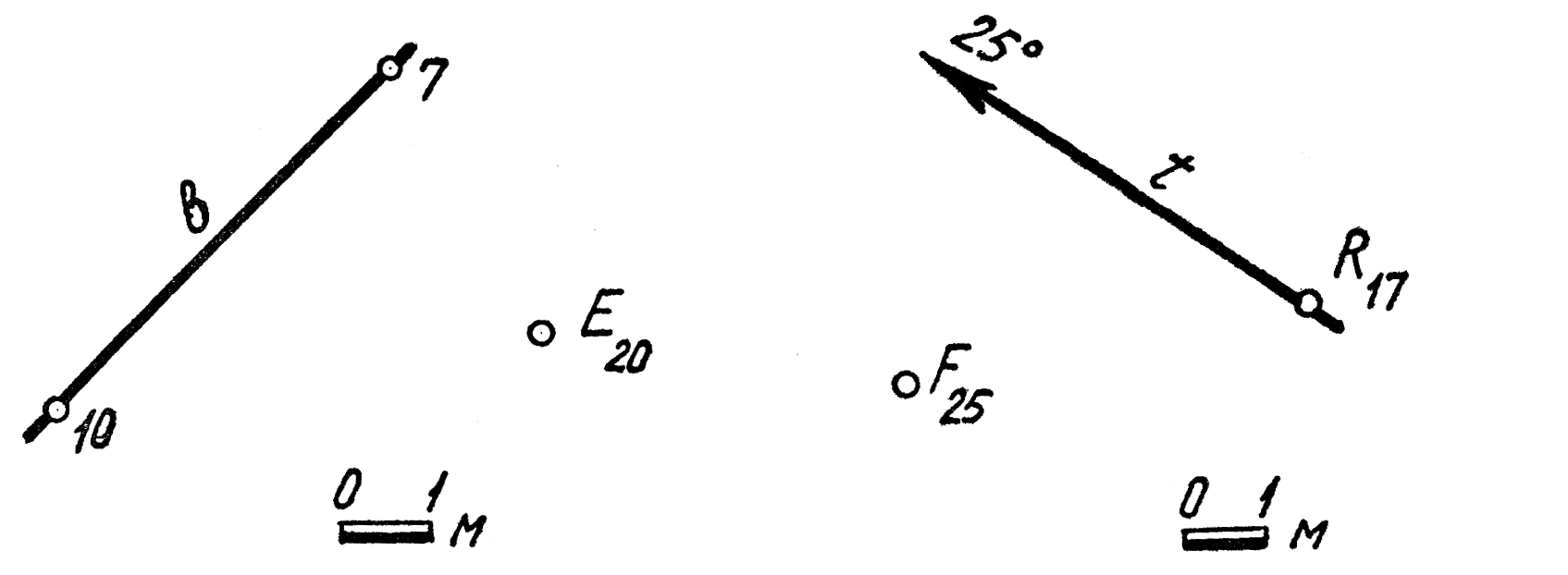
30. Определить элементы залегания плоскости К, которая проходит через точку Апараллельно скрещивающимся прямым lиt.
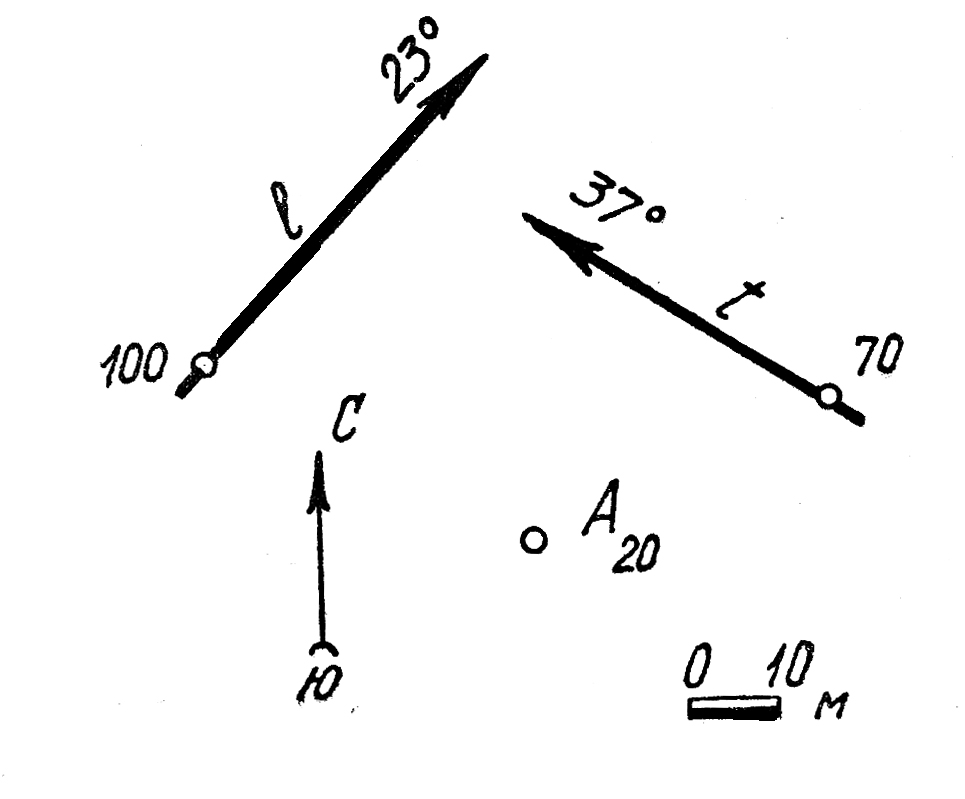
31. Через точку Апровести прямую т, которая была бы параллельна плоскости Σ и пересекала бы прямую t.
32. Провести произвольную прямую b, которая была бы параллельна плоскости Ωи пересекала бы прямые cиd
 
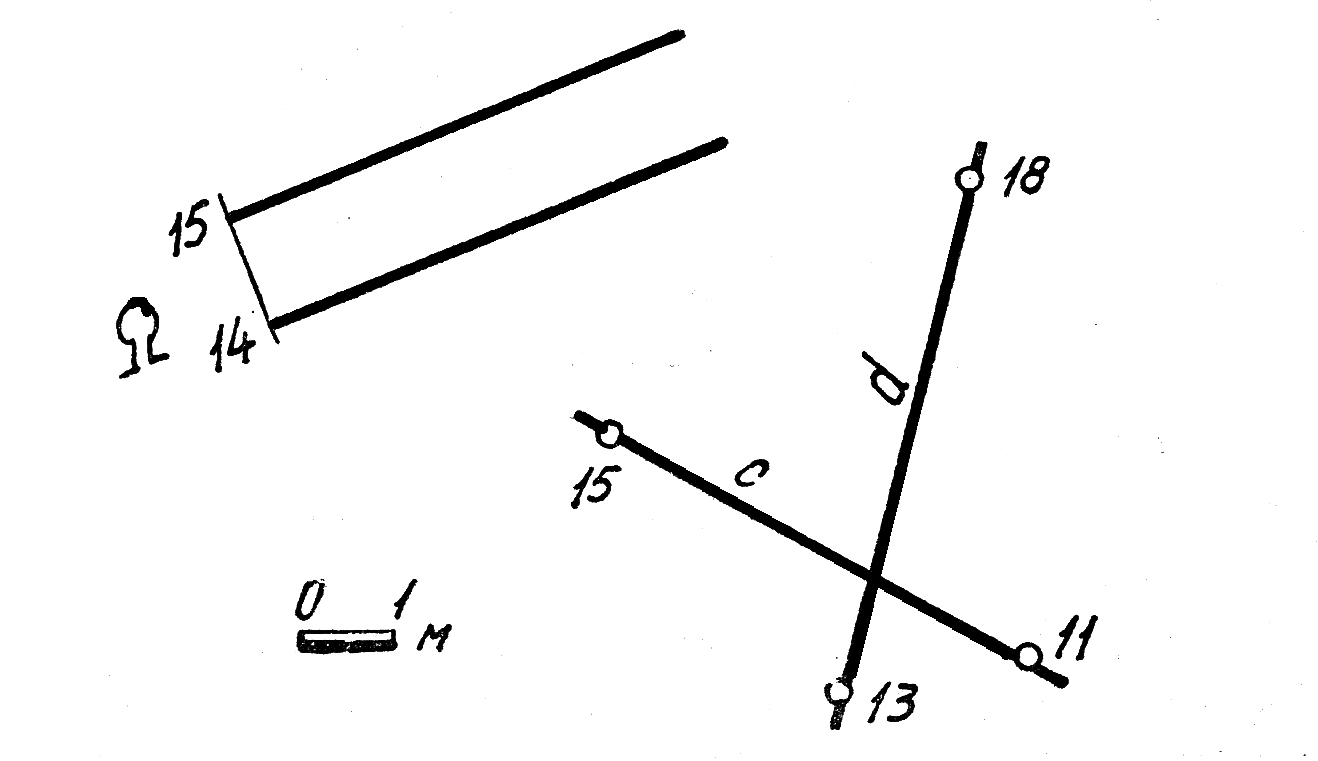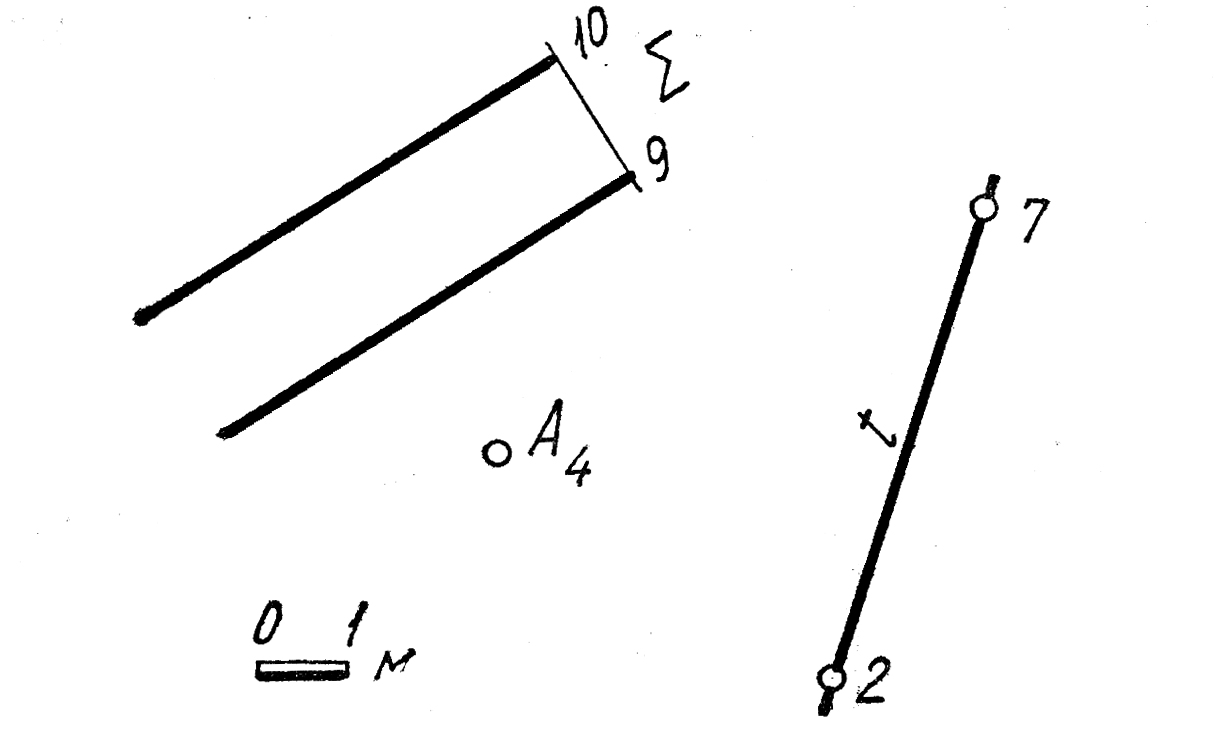
33. Построить точку Dпересечения прямой т(А12380) с плоскостью Ψ(a×b). Определить видимость прямой относительно плоскости.
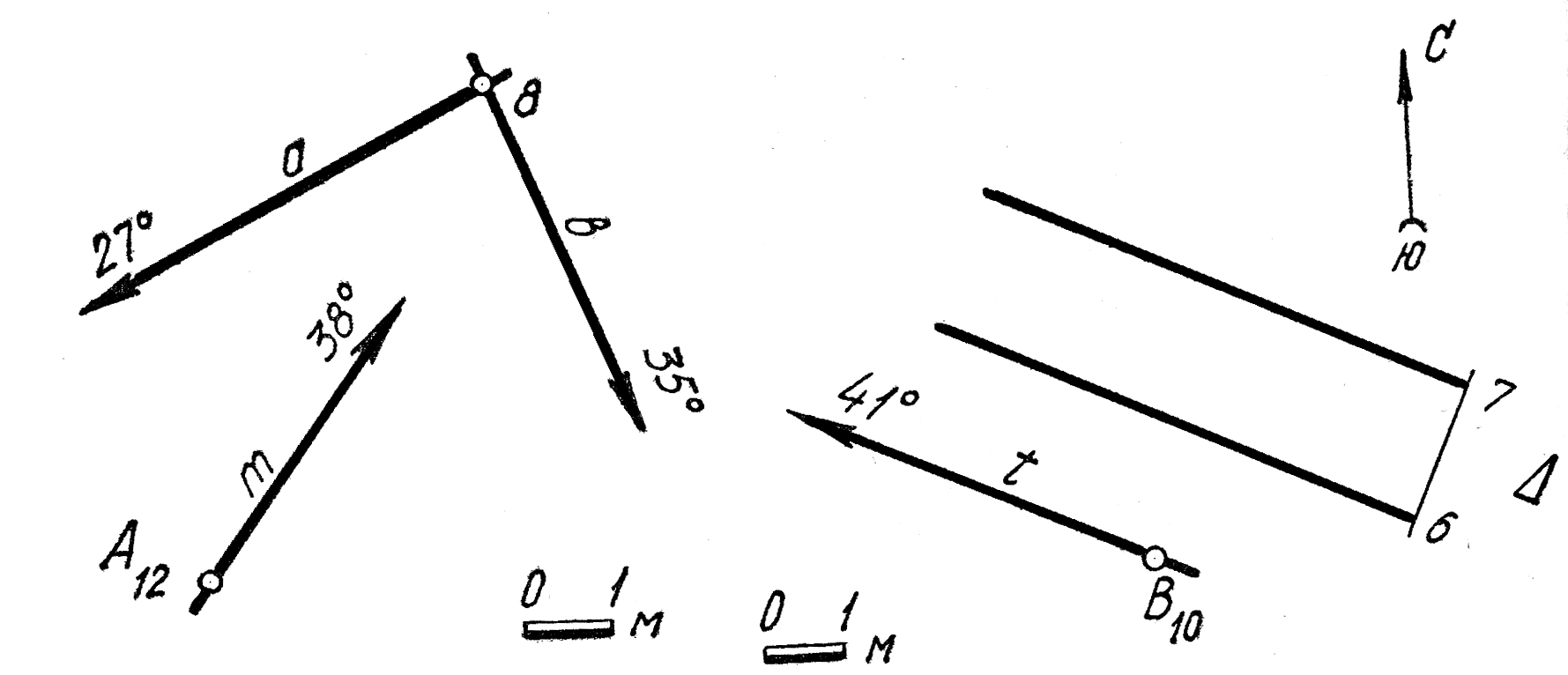
34. Прямая t(F4035°)пересекает параллельные плоскости Ω(F25 аз. пад. 260° 40°) и Т в точках Ри L, отстоящих друг от друга на расстоянии 10 м. Определить истинное расстояние между плоскостями Ω и Т.
35. Провести произвольную прямую l, которая пересекла бы три скрещивающиеся прямые а, bи с.
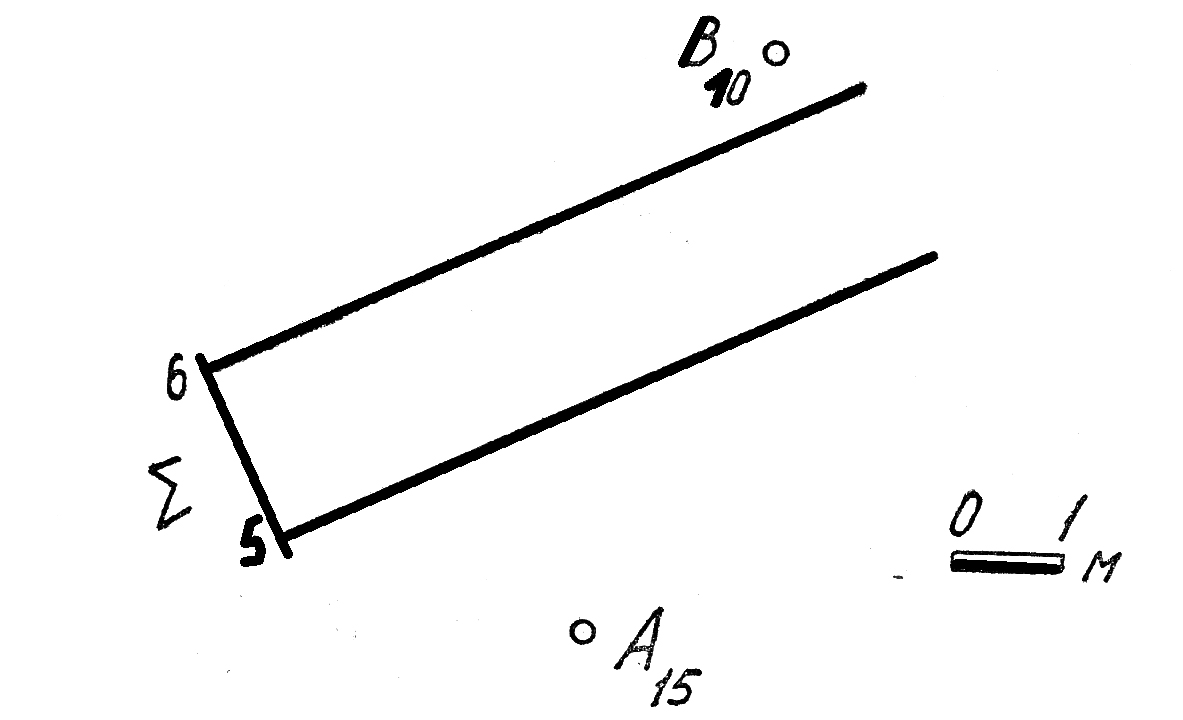
36. Определить истинное расстояние от точки Rдо плоскости Σ.
37. В плоскости Σ построить геометрическое место точек, равноудаленных от точек АиВ.
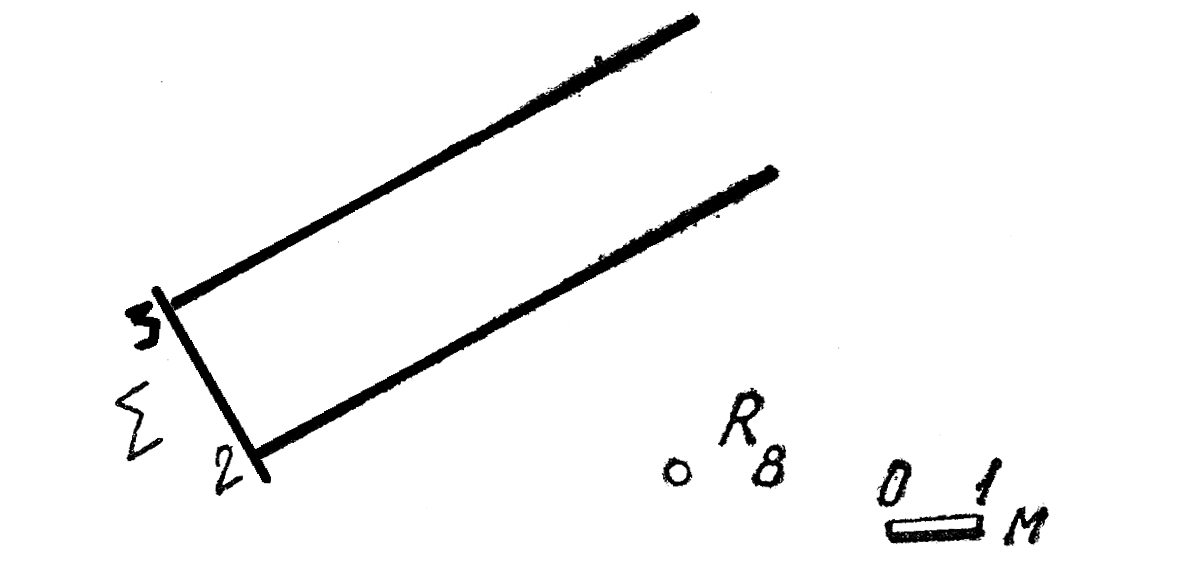
38. Построить прямую d, которая была бы перпендикулярна к плоскости Т и пересекла бы скрещивающиеся прямые rи f.
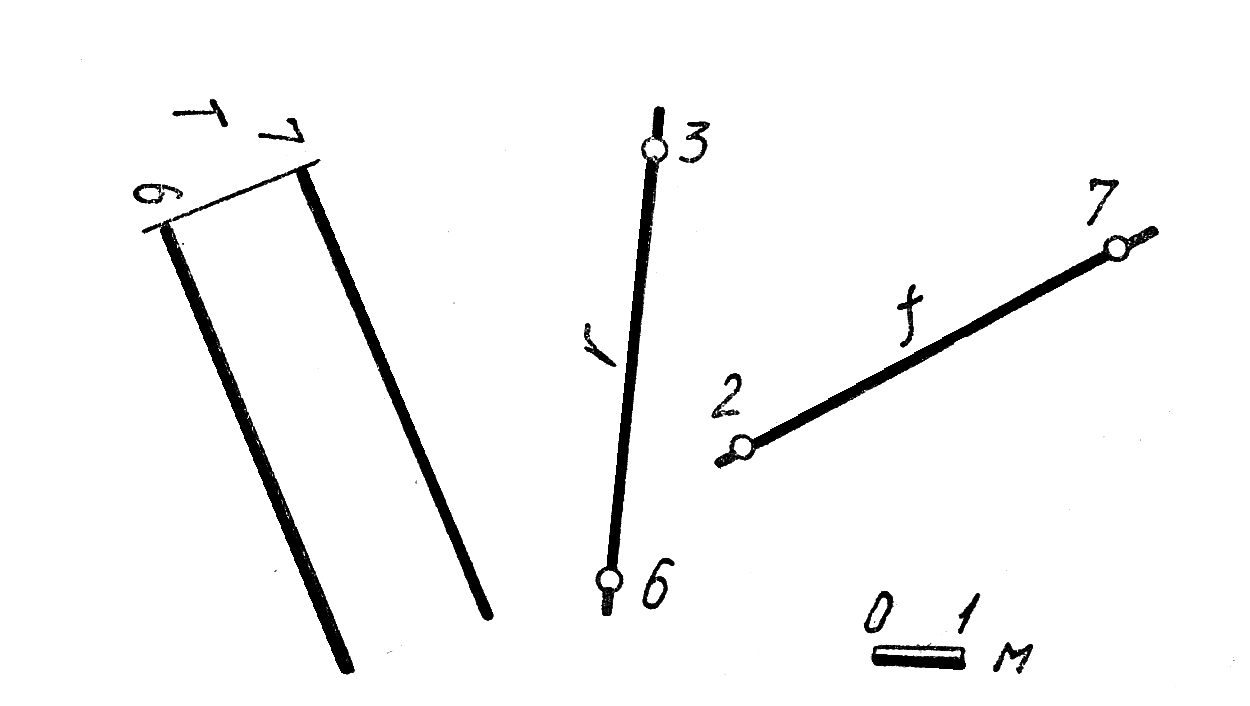
Метод вращения
39. На какой угол надо повернуть прямую m(F10370) вокруг вертикальной оси i, чтобы она пересекла бы прямую b.
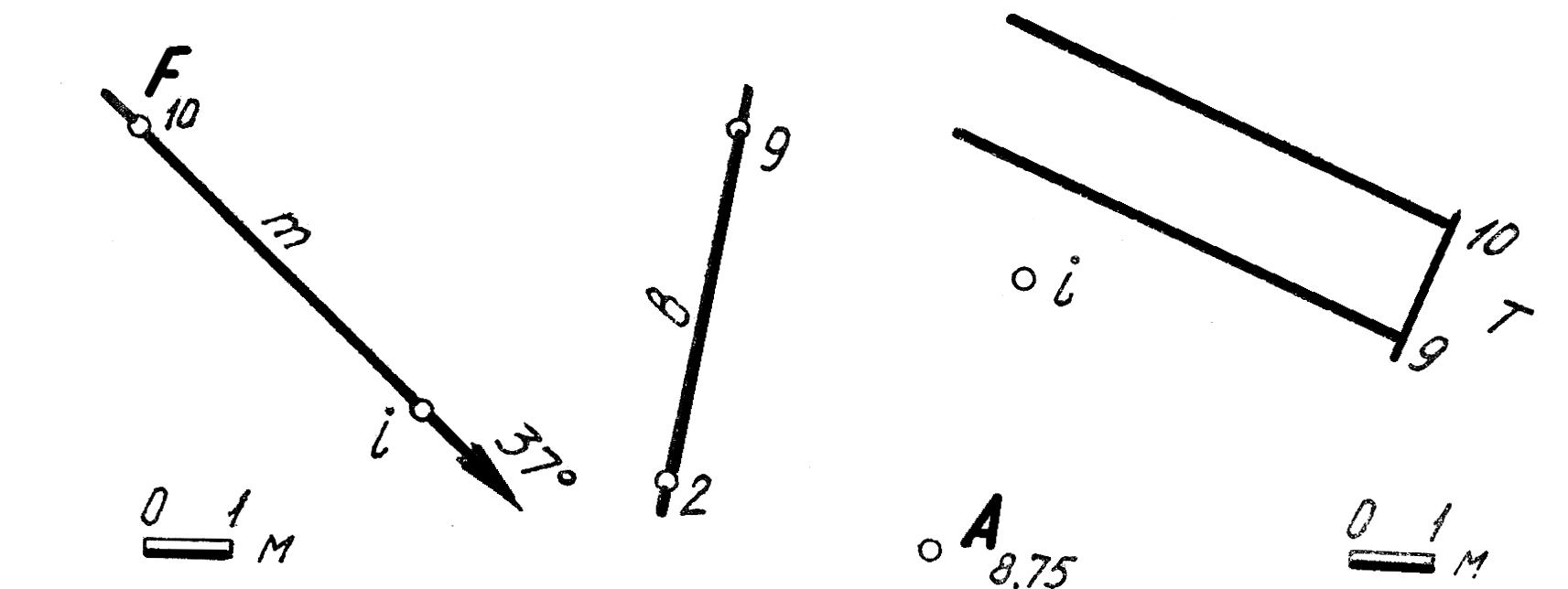
40. Вращением вокруг оси iточку Rсовместить с плоскостью Θ(В7,5 а).
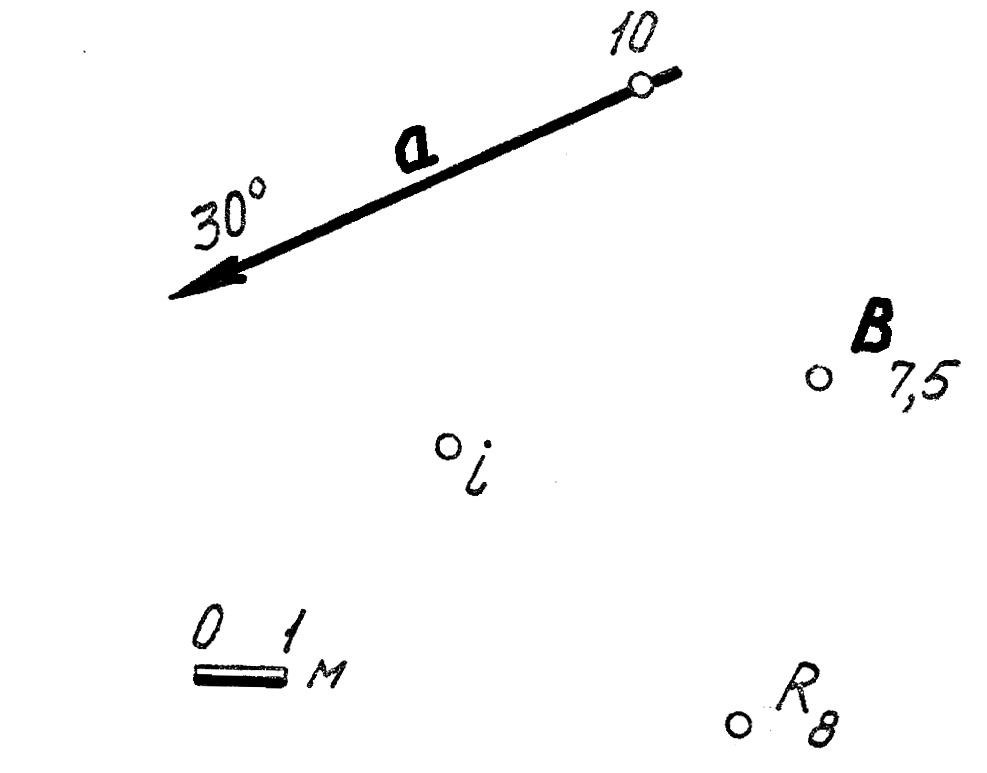
41. Вращением вокруг горизонтали плоскости Σ, отметка которой равна 4 м, прямую b(A4С7,5) совместить с плоскостью Σ.
42. Вращением вокруг горизонтальной оси hплоскость Т совместить с точкой С.
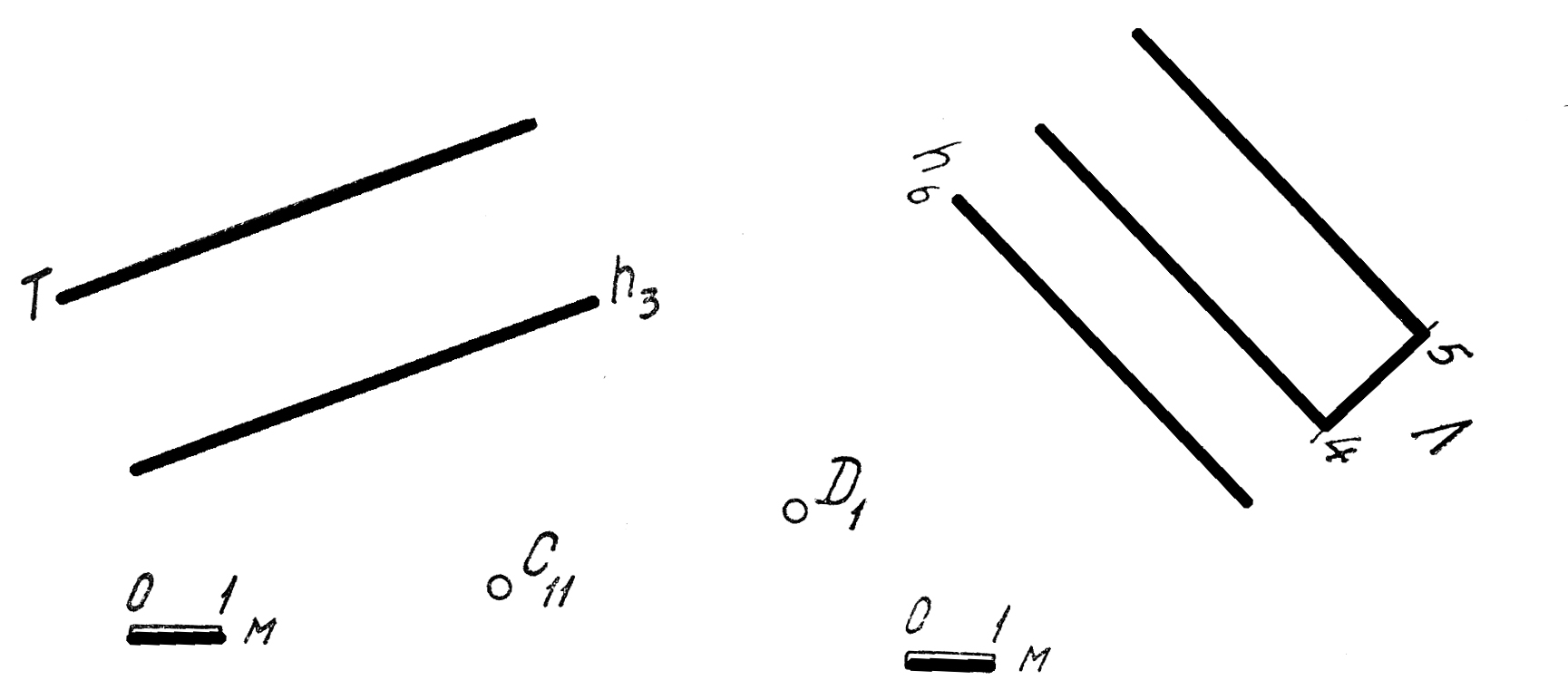
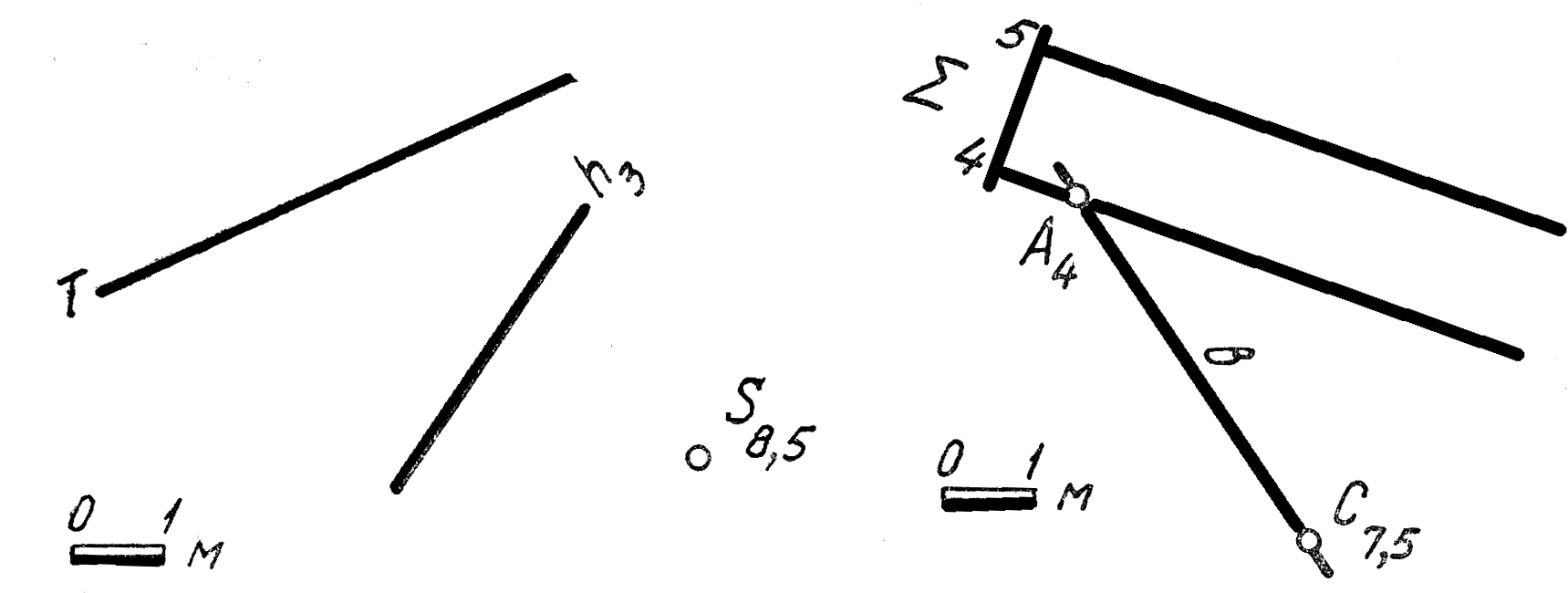
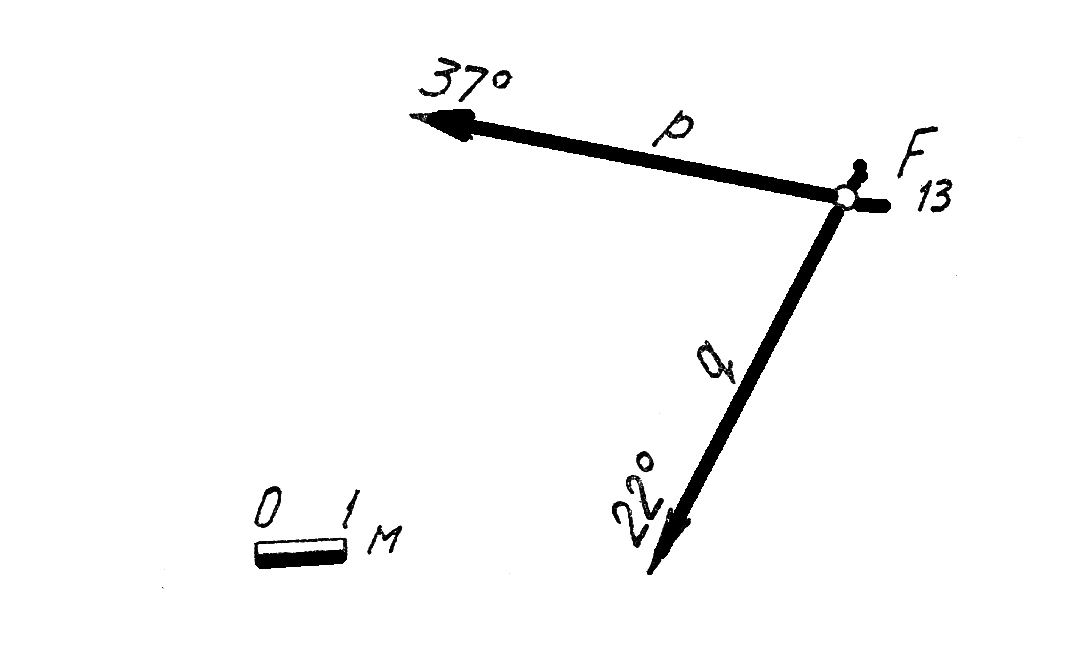
43. Построить проекцию биссектрисы линейного угла составленного прямыми p (F13370 ) и g(F13220)
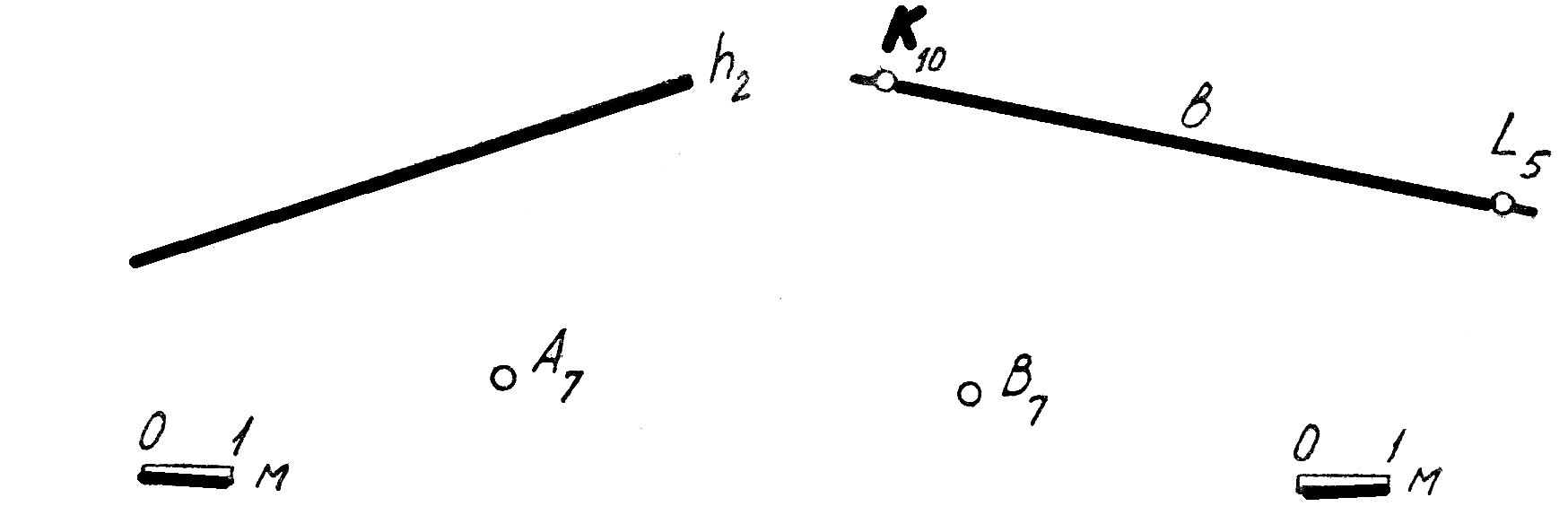
44. Через точку Впровести прямую п, которая пересекла бы прямую b(К10L5)под углом 28°.
 
45. Построить проекцию равностороннего треугольника ABC, лежащего в плоскости Σ, исходя из условия, что сторона AB треугольника длиной 8 м имеет угол падения 150 .
4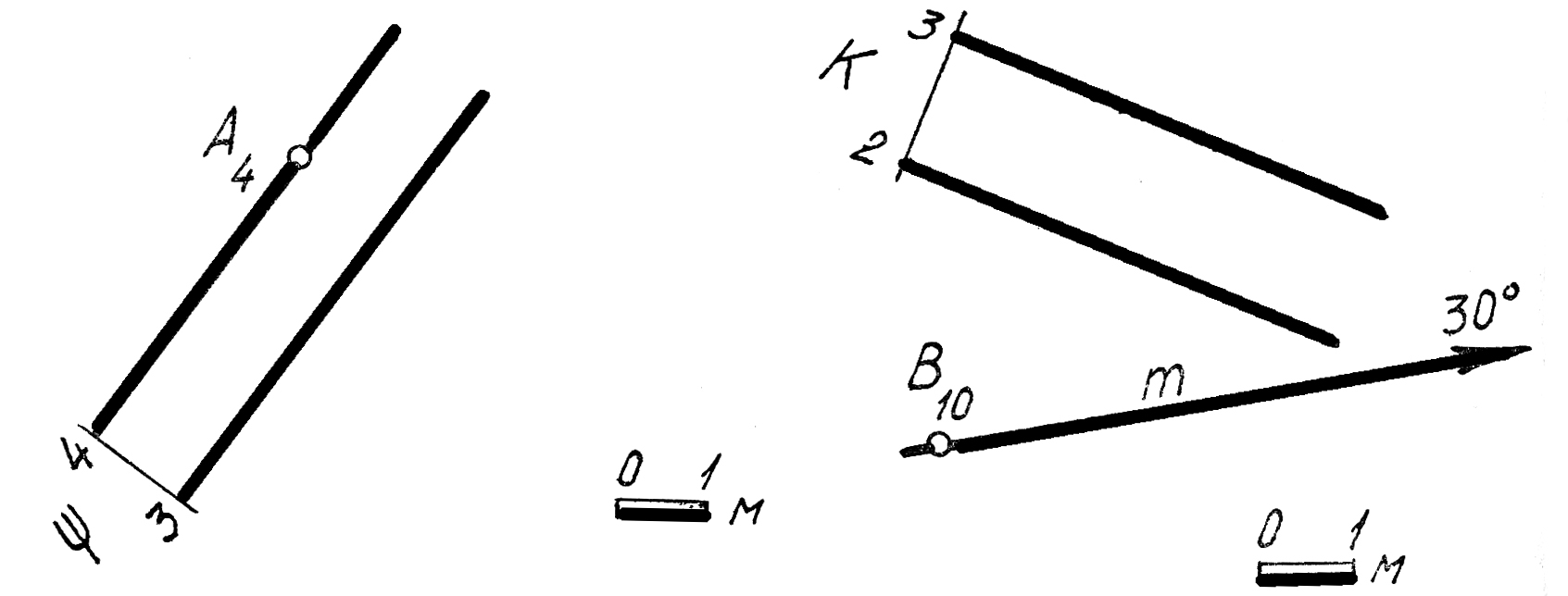 6.Определить истинную величину угла β, составленного прямой m(B10 30°) и плоскостью К.
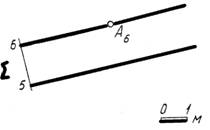
47. Определить истинную величину двугранного угла ΛnT
48. Определить элементы залегания плоскости Σ, которая проходит через точку Aи биссектрису линейного угла β(тп).
 
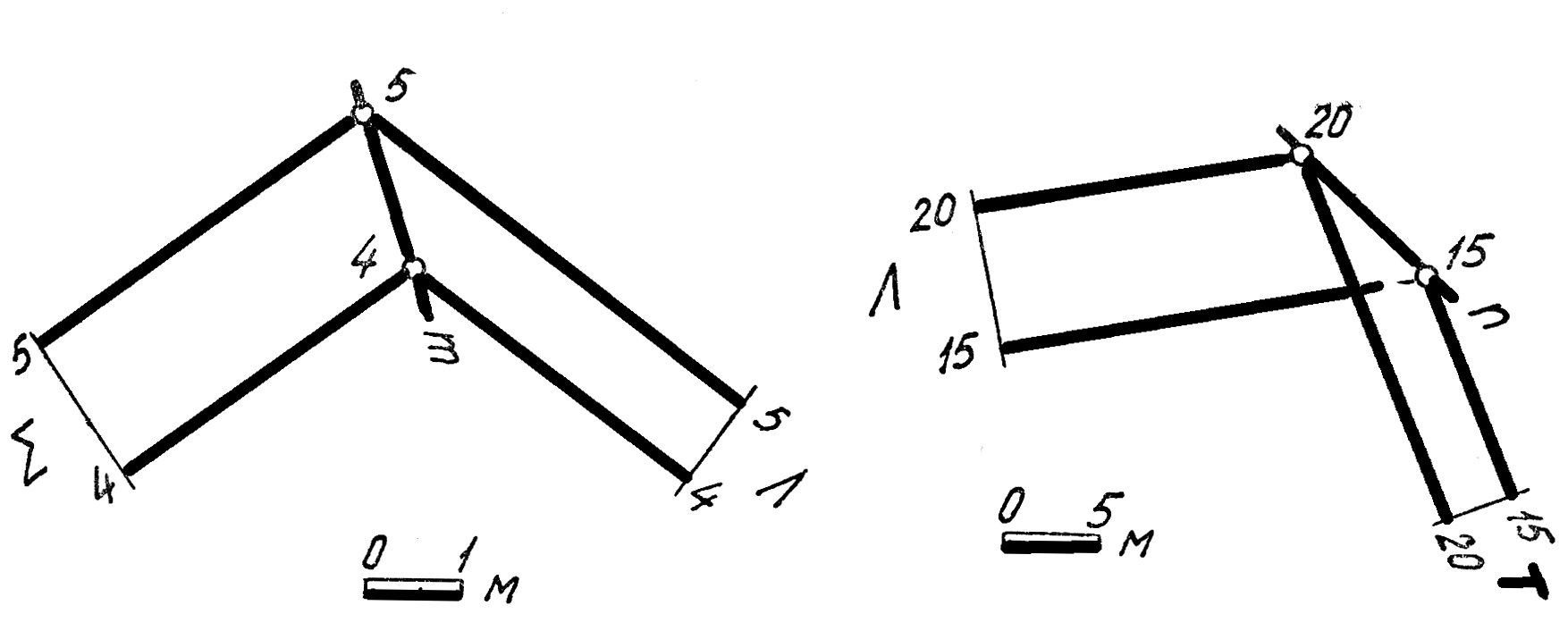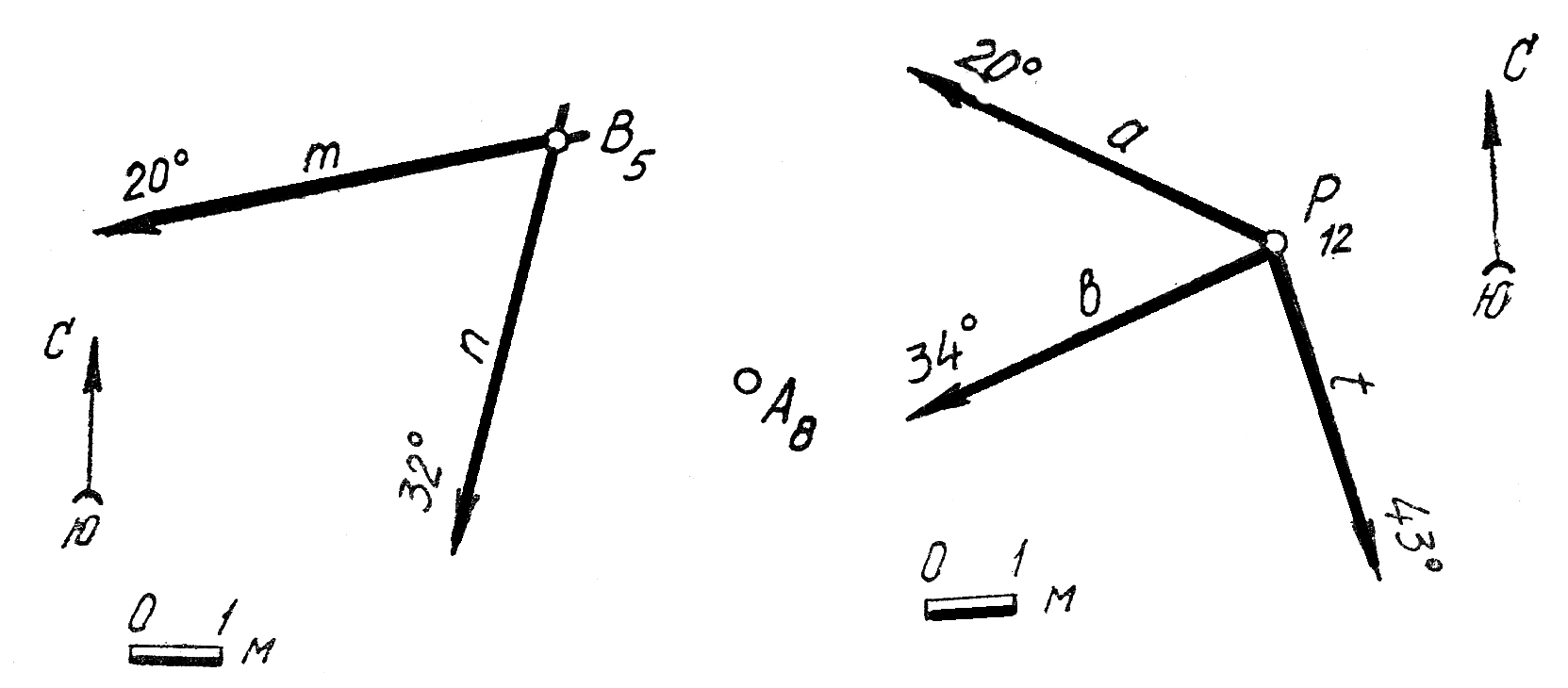
49. Определить элементы залегания биссектроной плоскости Δ двугранного угла YiФ.
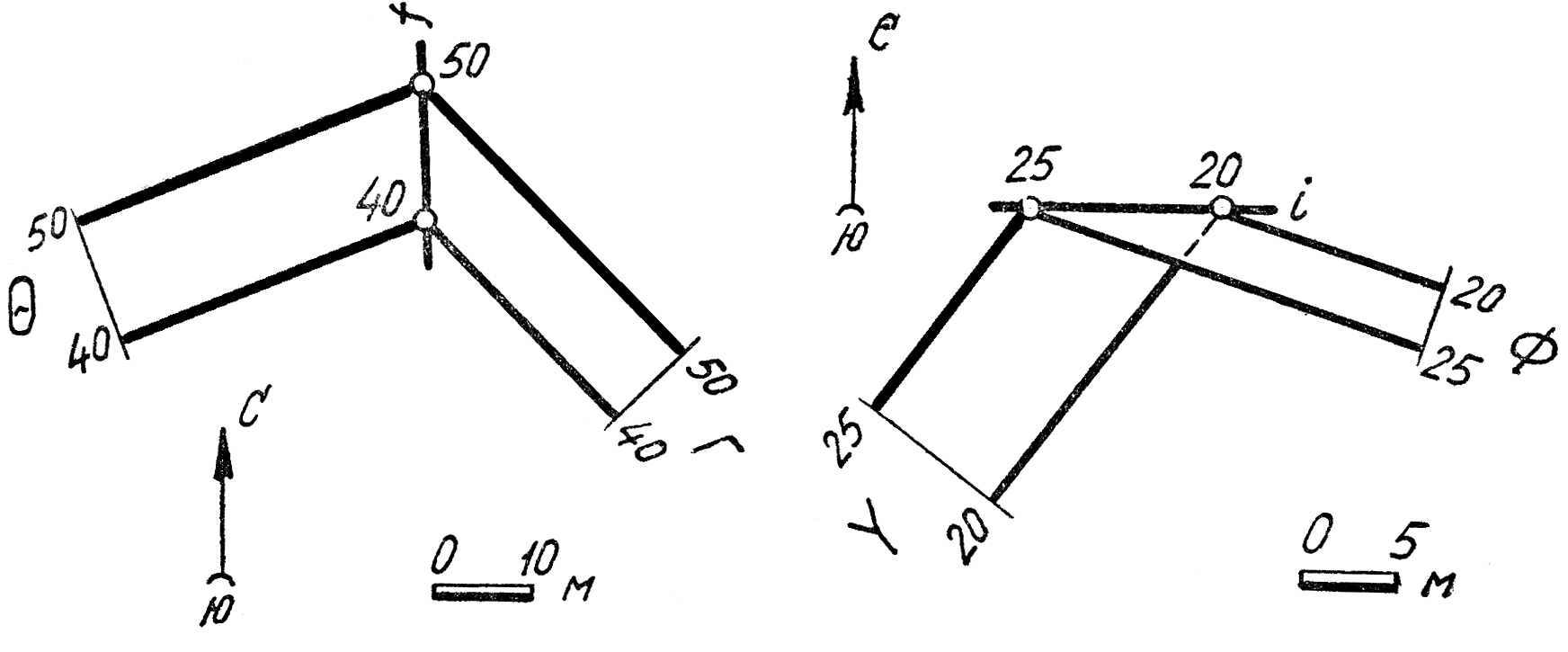
Пересечение поверхности с плоскостью
50. Построить истинный вид фигуры сечения наклонной пирамиды плоскостью Т.
51. Построить истинный вид фигуры сечения многогранника вертикальной плоскостью Т, проходящей через прямую b.
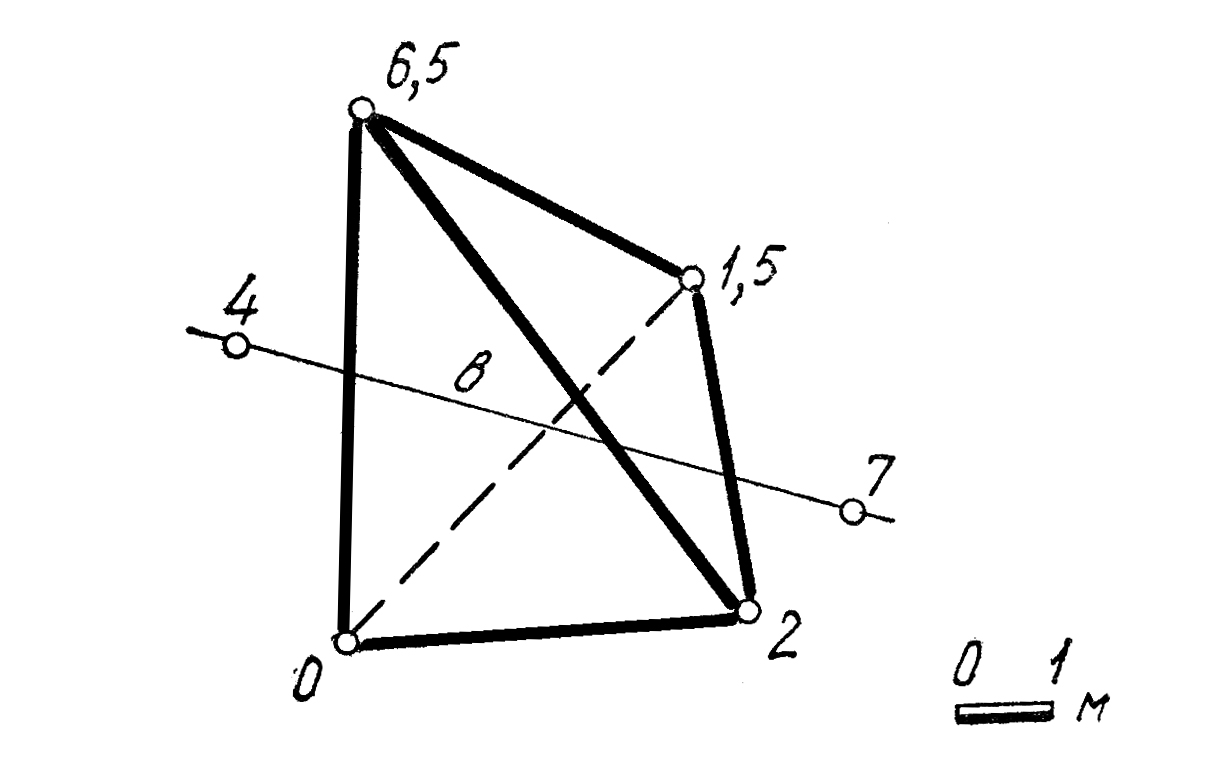
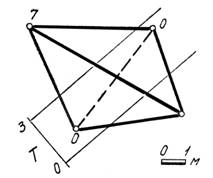
52. Построить: 1) линию пересечения топографической поверхности с плоскостью Λ (В105 аз. пад. 2350 480),Профиль разреза по линии М-М1.
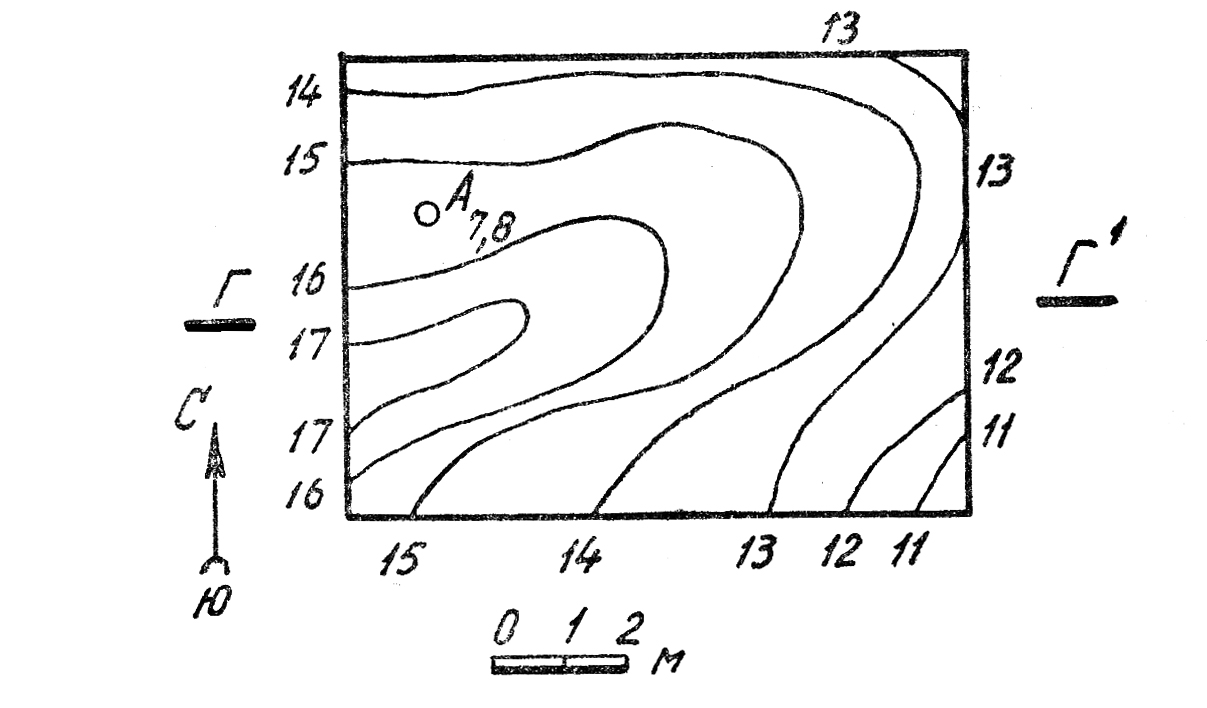
53. Построить: 1) линию пересечения топографической поверхности с параллельными плоскостями Σ(А7,8 аз. прост. 160° 90°) в отстоящих друг от друга на расстоянии 6,5 м; 2) профиль разреза по линии Г—Г1.
 
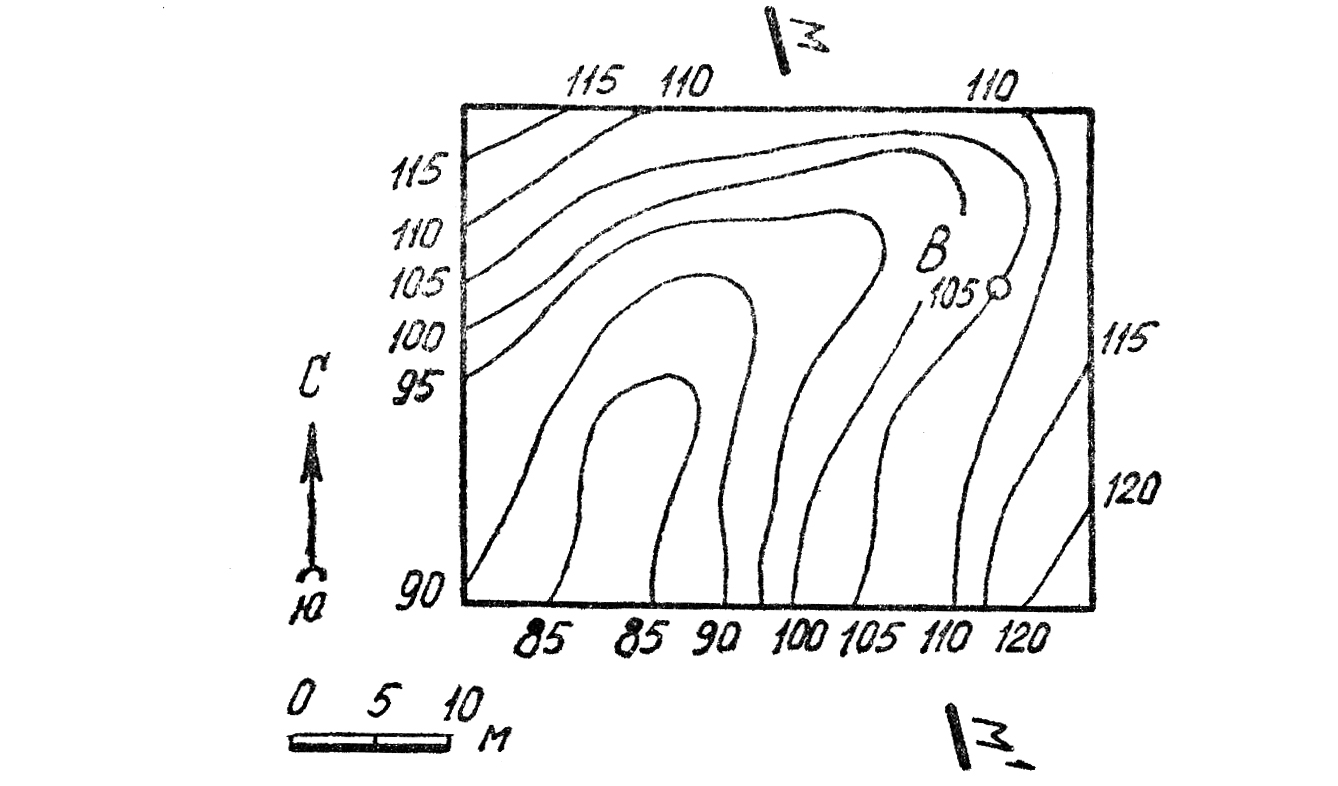
54. Построить: 1) линии пересечения топографической поверхности с параллельными плоскостями Θ(С90аз. пад. 210° 420) и Z. Плоскость Z расположена под плоскостью Θ на расстоянии l0 м; 2) профиль разреза по линии К—К1.
|
Скачать 28.52 Mb.